图像空洞填补算法及其FPGA硬件实现
伍能举, 徐 栋, 杨依忠
(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601)
在2D图像通过基于深度图像绘制(depth image based rendering,DIBR)方法转换成左右视图时[1-2],左视图和右视图中会出现空洞点。空洞是图像中像素值与周围像素相比异常并且会给视觉带来不适的图像像素,因此在目标图像绘制时需要进行图像空洞的填补。空洞点通常为固定大小的值,即像素值为0,极少数不为0的空洞像素值也小于一定的阈值。在空洞填补时,通过对像素值与规定的阈值进行比较,判断像素点是否属于空洞点,再对其进行处理。处理空洞主要分为深度图预处理和空洞填补2个步骤,深度图预处理一般通过滤波来平滑深度图以减少3D图像的失真[3],但是滤波无法解决深度图中前景与后景深度差异大而导致的空洞。对空洞的简单填补也可以通过滤波算法[4-5]来进行处理,但是滤波会造成图像的模糊而丢失一些细节,从而影响视觉效果。整体变分法[6]能够修复图像中的空洞点,但是该方法是通过迭代修复来实现的,因此存在计算量大、耗时长等问题。基于样本的图像空洞修复[7]对纹理丰富的图像中的空洞能有效地修复,但是对图像纹理有一定的要求。文献[8]提出通过插值相邻像素点来进行空洞填补的方法,该方法易于实现,但是没有考虑到邻域像素中也会存在空洞点的问题。
本文提出一种DIBR方法绘制目标视图中的空洞填补算法,算法步骤如下:先通过深度梯度过渡方法对简单滤波后的深度图进行预处理,减少目标视图中的空洞;再考虑填补像素中空洞点数量的不同,分别设置对应的权值,给出对应的填补方法。传统的图像空洞填补技术是基于软件的方法,现场可编程门阵列(field programmable gate array,FPGA)的发展给图像处理提供了良好途径[9-10],它具有高速的并行运算能力,可以用来进行图像硬件实现[11-14]。本文算法同时在Matlab软件平台上和FPGA硬件平台上进行验证,实验结果表明填补效果良好。
1 算法设计
本文算法包括深度梯度过渡和空洞填补2个部分,深度梯度过渡是一种有别于其他预处理的方法,可以适当减少深度图前景与后景深度差异造成的空洞,为后续空洞填补算法高效运行提供良好基础;空洞填补算法充分考虑到邻域插值填补像素中存在空洞点的问题,可更加合理有效地对空洞进行填补。
1.1 深度梯度过渡
DIBR虚拟视点绘制通过深度图与参考图像绘制目标图像,目标图像为左视图或右视图。针对目标视图中前后景边界空洞,采用前景与后景深度边界梯度过渡的方法来减少空洞。算法针对左视图进行处理,若为右视图则边界判断方法一致,过渡方向改为向右。深度图中的前景与后景边界需要通过相邻像素深度值的差值来获得,若其差值大于预先给定的阈值d0,则认为此处为前后景边界处,公式如下:
Dd(i,j)=
(1)
其中:D(i,j)为深度图中在位置为(i,j)处的深度值;Dd(i,j)为前景与后景的边界。通过前景与后景的深度梯度过渡,可以减少由于深度图中的前景与后景边界深度值变化剧烈导致的空洞。深度梯度过渡公式为:
D(i,j-k)=[D(i,j-k-1)+D(i,j)]/2
(2)
当Dd(i,j)=1时,说明深度图中前景与后景边界已经进行了标记,对标记位置进行深度梯度过渡,其中k为深度梯度过渡的步数,实验中将k值设为5时,边界空洞基本不再变化。深度梯度过渡后需要对过渡的边界进行阈值判断,目的是使过渡后的边界满足平稳变化的条件。阈值判断公式为:
|D(i,j-k)-D(i,j-k-1)| (3) 其中,a为阈值。若不满足条件则继续过渡。 图像中的空洞点可以认为是受损的像素点,该位置的像素点与其周围的像素点存在较大的关联,因此,可利用周围像素点与空洞点的关系来进行填补。本文提出一种改进的邻域像素空洞填补方法。由于空洞点多为纵向连续分布,即空洞点的上方和下方大概率也存在空洞点,如果只是使用空洞像素的8个邻域像素点,将无法充分利用其周围信息,故在横向上额外增加A2、E22个像素作为空洞填补的参考像素。考虑到离空洞越近的像素点与空洞的相关性越强,因此赋予离空洞像素点位置远的填补像素较小的权值,对离空洞近的填补像素点赋予大权值以保证填补的效果。由2D图像通过DIBR方法转换生成的左视图与右视图仅仅是视差不同,空洞填补的方式一致。空洞与邻域填补像素的关系如图1所示。 图1 空洞与邻域填补像素的关系 若C2为空洞点,使用B1、C1、D1、B2、D2、B3、C3、D3、A2、E2这10个像素进行空洞填补。但填补像素中依然可能存在空洞点,且通常这10个像素不会都是空洞点,则需要对填补像素中的空洞点数量进行讨论,根据填补像素中空洞点的数量不同,给出不同的填补方法。若填补过程中这10个像素点中无空洞,则填补公式为: C2=(B1+C1+D1+B2+D2+B3+ C3+D3)w1+(A2+E2)w2 (4) 记C2的8像素邻域中的空洞数目为m,A2、E22个像素中空洞数目为n,考虑到填补像素中空洞点数量对填补效果的影响,若m<8且n<2,则空洞填补公式为: D2+B3+C3+D3)+ (5) 若m=8且n<2,则空洞填补公式为: (6) 若m<8且n=2,则空洞填补公式为: D2+B3+C3+D3) (7) 根据以上方法可以对图像中的空洞点进行有效填补,弥补了邻域像素空洞填补方法中没有考虑邻域填补像素存在空洞点的问题。 本算法的硬件实现是基于FPGA平台,使用Altera的Cyclone IV EP4CE15开发板,该开发板具有15×103个逻辑单元、4 Mibit的SRAM、256 Mibit的SDRAM以及时钟管理单元等资源。算法的硬件设计包括3×5窗口模板生成模块、空洞判断与填补模块,最后进行了VGA的显示。原理结构如图2所示。 图2 空洞填补FPGA原理结构 输入图像数据流为灰度图,其灰度值范围在0~255之间,通过移位寄存器生成3×5的窗口模板,利用窗口模板对空洞进行判断和填补,最后通过VGA显示输出实验结果。 因为与在软件中对图像进行处理的方式不同,硬件中的图像信息是以数据流的方式进行传输的,与时钟周期有关,1个时钟周期只能发送或者接收1个像素数据,从而无法一次性对整幅图片进行处理,所以需要设计窗口模板来进行相应的像素处理,并通过窗口模板的滑动来实现对整幅图片的空洞填补操作。为了得到3×5窗口模板,使用先进先出(First-In- First-Out,FIFO)队列来作为图像数据的缓冲器。实验中通过调用Quartus II软件中的基于RAM的移位寄存器宏模块altshift-taps实现行延迟以生成 3×5窗口模板。进行缓存的深度设置为输入图像的行像素总数。这样1个时钟周期里通过3个移位寄存器可以输出3个像素数据,通过5个时钟周期可以输出15个像素数据,满足了生成3×5的窗口模板,在模板中可以对这些像素进行空洞判断和填补。 3×5窗口模板可以取到15个像素数据,如果像素是空洞就利用这模板中的10个像素数据进行空洞填补。图像的空洞填补运算需要利用卷积与求和的计算方法,通常可以通过触发器、加法器和乘法器的硬件设计来进行相应的数学运算,但该方法比较繁琐,本文采用可编程乘加法器和可编程多路并行加法器等来实现空洞填补需要的数学计算。空洞填补的移位寄存器像素运算结构如图3所示。 图3 空洞填补运算结构 空洞填补运算结构由3个基于移位寄存器的Line Buffer、10个可编程乘法器及4组并行加法器构成。Line Buffer0、Line Buffer1和Line Buffer2对输入图像数据中相邻的3行像素分别进行缓存,模板中邻域像素值与w1相乘,非邻域像素值与w2相乘,通过可编程多路并行加法器处理数据后即可得到空洞的填补值。具体地,当图像数据输入时,图像数据在时钟控制下并行传递到后续的寄存器,持续5个时钟周期后生成3×5的窗口模板,此时Line Buffer0中B1、C1、D1的输出与w1并行相乘,相乘得到的数据再并行相加,并行相加的输出为S1,为空洞填补结果的一部分。同理Line Buffer1和Line Buffer2也经过乘加运算分别得到S2、S3,最终S1、S2、S3通过并行加法器运算得到空洞填补的结果。 3.1.1 深度梯度过渡结果 为了验证算法深度梯度过渡的效果,在Matlab软件平台上对图片进行了实验。实验选取的图片是在2D转3D过程中生成的左视图,目标视图中存在空洞。图片的名称为Ding,分辨率为1 024×768。深度梯度过渡后局部对比如图4所示。从图4可以看出,通过深度梯度过渡处理减少了位于雕像左侧前景与后景边界的空洞数量,同时提高了视觉效果。 图4 深度梯度过渡后局部对比 3.1.2 空洞填补 由空洞填补公式知,因为空洞填补使用10个像素作为填补像素,所以填补参数w1、w2应满足8w1+2w2=1的条件,由填补时像素与空洞远近关系知w1>w2,w1的范围在0.100~0.125之间,w2的范围在0~0.1之间,w1的值分别选取0.105、0.110、0.115、0.120进行试验,以获得最佳的参数。使用峰值信噪比(peak signal-to-noise ratio,PSNR)对填补后的图像进行评估,当w1取0.115时,得到较好的PSNR值。对图片Ding进行空洞填补前后的实验结果如图5所示。 图5 Ding图片实验结果 对比图5a、图5b可知,通过算法能有效地去除图像中的空洞。对Ding实验结果与加权均值滤波算法[5]、整体变分算法[6]及基于样本的填补算法[7]的结果进行了比较,结果见表1所列。 表1 空洞填补参数比较 因为滤波会导致图片模糊而丢失图片的部分细节,使用这种方法进行空洞填补将会导致填补后的目标视图视觉效果不理想,所以使用滤波方法来处理图片中的空洞并不合适。本文算法只针对空洞进行处理,能很好地保存图片细节部分。由表1可知,本文算法的PSNR为38.64 dB,高于其他算法,均方误差(mean square error,MSE)为8.90,低于其他算法,本文算法的PSNR与MSE性能指标优于其他3种算法。 硬件实现及测试实验使用Altera的Cyclone IV EP4CE15 FPGA开发板。SD读卡模块、异步FIFO读写模块与SDRAM读写模块、空洞填补算法模块、VGA显示模块共同构成完整的实验系统。联机调试前,先对代码进行了波形仿真,使用ModelSim软件对算法仿真的结果如图6所示。 图6 空洞填补仿真波形 从空洞填补仿真波形可以看出,在输入完整的15个像素窗口模板数据后,对空洞像素C2进行填补,填补前的像素值为二进制数,值为00000000(十进制为0),填补后该位置的像素二进制数值为10011111(十进制为159),不再是空洞像素。同时,将填补后的像素值与其上、下、左、右4个像素值进行比较,观察填补后的像素与其周围的像素是否差异过大。若差异过大则可能造成填补后位置的像素视觉效果差。空洞上、下、左、右4个位置如下:B2为10101001(十进制169);C1为10101001(十进制169);D2为10101111(十进制175);C3为10100011(十进制163),因此填补后的像素值C22与周围像素在梯度变化上差异小,不会造成不良的视觉效果。为了测试空洞在硬件上的填补效果,将代码用Quartus 软件下载到FPGA开发板进行测试,填补前与填补后的结果如图7所示。从图7可以看出,在FPGA硬件平台上能有效地填补图片中的空洞,没有视觉不适的现象,效果良好,同时,空洞去除后,对图片中的其他细节并没有造成影响。因此,设计的空洞填补算法在FPGA硬件平台上也能针对图片空洞进行有效的填补。 图7 FPGA空洞填补前后结果 本文针对DIBR方法绘制后的目标视图存在空洞的问题,提出了一种对目标图像空洞有效填补的算法,先对深度图前景与后景边界中存在的空洞进行深度梯度过渡预处理,然后利用空洞点与周围像素关系,即根据与空洞像素距离设置不同的权值w1、w2,并且考虑填补像素中的空洞数量,给出不同填补方法。最后将该算法在Matlab软件平台上和FPGA硬件平台上分别进行了验证,实验结果表明填补效果良好。1.2 空洞填补
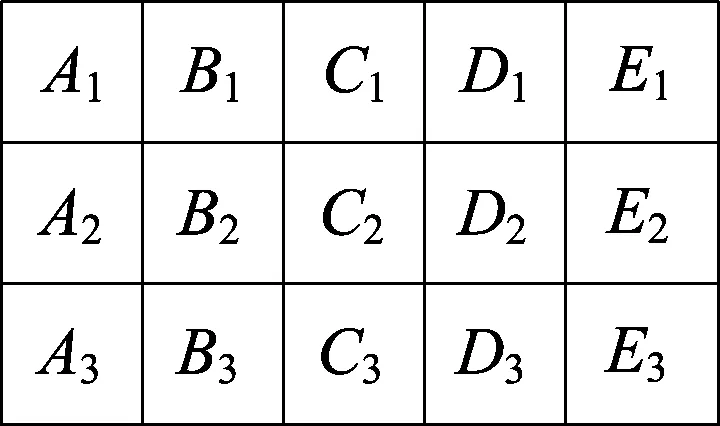
2 软件算法的硬件FPGA实现

2.1 3×5窗口生成模块
2.2 空洞填补模块

3 实验结果与分析
3.1 软件实验结果及分析



3.2 硬件实现及测试



4 结 论

