基于M-DTCWT和2APCNN的多聚焦图像融合

钱荣威, 许丹丹, 周 涵

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

多聚焦图像融合技术能够有效提高图像信息的利用率和系统对目标探测识别的可靠性，是图像融合研究中一类具有代表性的研究问题[1-2]。图像融合方法主要分为空间域算法和变换域算法。空间域算法主要有灰度加权平均法、主成分分析法(PCA)和针对遥感图像通道形式的颜色空间转换法(HSV)等[3-5]。基于空间域的融合算法直接对图像像素进行简单处理，即将图像中清晰区域与另一幅图像的模糊区域进行加权平均容易导致图像信息的丢失，对融合图像的质量产生较大影响。变换域算法主要有Laplace金字塔变换法、小波变换(WT)法、轮廓波变换(CT)法及非下采样轮廓波变换(NSCT)等方法[6-7]。由于变换域算法在提取图像细节上具有更多的优势，因此被广泛应用与多聚焦图像融合中。但传统小波只能捕获有限的方向信息，不能有效反映丰富的方向纹理。双树复小波变换(DTCWT)[8]的提出极大减小了传统小波变换中的平移敏感性。吴一全等[9]将DTCWT与CT中的方向滤波器组(DFB)进行级联得到了具有移不变性的复轮廓波变换(CCT),但因DFB存在下采样行为，所以会在一定程度上影响图像融合效果。采用非下采样滤波器组(NSDFB)替换CCT中的DFB，得到一种不具有非下采样行为的多方向双树复小波变换(M-DTCWT)，将其应用于多聚焦图像融合中，可对图像进行更多尺度和方向上的分解，因此它能够更好地提取多聚焦图像的边缘细节等高频信息，从而提升融合质量。在图像融合过程中，除分解工具以外，对分解系数的融合策略同样对融合质量起着举足轻重的影响。随着压缩感知的发展，稀疏表示(SR)为图像融合提供了新的方法。Yang et al[10]在DCT(discrete cosine transformation)字典下建立稀疏分解模型，采用OMP算法得到稀疏系数，但此方法未进行多尺度分解，直接在原图像基础上进行稀疏表示，容易丢失图像细节。Moonon et al[11]在对稀疏系数融合时，采用系数绝对值取大策略时未考虑单组系数间的相关性，因此本文采用模糊逻辑(FL)与SR相结合的方法(FAR)作为低频系数的融合策略。脉冲耦合神经网络(PCNN)是一种模拟动物大脑皮层细胞的神经网络模型，具有空间邻近和特征相似聚集的特点，广泛应用在图像高频系数组的融合中[12]，文献[13]提出了双通道脉冲耦合神经网络(2APCNN)简化了PCNN模型，文献[14]将其应用在了多聚焦图像融合中，提升算法计算效率的同时得到了较好的融合效果。本文将平均高斯差分梯度(ADOG)作为2APCNN的链接强度，提出改进2APCNN的高频融合策略。

1 M-DTCWT的图像分解原理

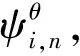
(1)

式中，θ∈{±15°，±45°，±75°}；n∈Z2；i∈N,表示分解尺度，N为分解总尺度。对图像进行DTCWT分解,每个尺度i都会产生2个低频子带与6个高频子带，一般将2个低频子带合并为1个低频子带，有利于下一级的尺度分解。

(2)

式中，n∈Z2；m∈Z2，各尺度下方向子带的分解数目为2l。由于NSDFB采用二叉树进行子带分解，所以会产生2n个方向子带。整体的分解结构如图1所示。

图1 M-DTCWT的整体分解示意图

2 2APCNN原理

根据生理学和心理学视觉系统对特征明显区域的反应要比不明显区域反应强烈，不可能每个神经元的链接强度都相同，而图像的梯度可以很好地反映边缘特征信息。针对传统PCNN缺点，提出一种改进2APCNN模型，将平均高斯差分梯度(ADOG)作为2APCNN的链接强度自适应选取通道，并提出改进空间频率(MSF)作为外部激励。其数学表达式如下

(3)

改进空间频率

(4)

式中，

(5)

式中，M×N代表图像尺寸；I(i,j)为(i,j)处分解系数。MSF既包含了行频RF、列频CF，也包含了对角频DF1、DF2。

平均高斯差分梯度

(6)

式中，(i,j)为像素坐标；P、Q=1为窗口大小；IDOG(i,j)为I(i,j)的二阶高斯差分。

(7)

式中，Gauss(x,y,σ)为二维高斯函数，根据式(6)得到链接强度

(8)

3 融合规则

3.1 结合FL与SR的低频系数融合

稀疏表示的模型

Xi=arg min‖X‖0 s.t,‖i-DX‖2<εi∈(A,B)

(9)

式中，i为源图像；D为过完备字典；X为稀疏系数；‖X‖0为稀疏向量的0范数；ε为逼近系数容限且ε≥0。然而，式(9)是一个NP-hard问题，为解决这一问题提出了基追踪(BP)算法、匹配追踪(MP)算法和正交匹配追踪(OMP)算法[16]。利用具有较高计算效率及收敛能力的OMP算法进行稀疏分解。

由于高斯函数作为图像所含信息及区域能力的一种测度，可以描述图像低频信息的丰富度，所以将归一化的高斯函数作为基本逻辑参考标准指导稀疏系数的融合。定义隶属函数如下

(10)

式中，μ、σ2分别为稀疏向量均值、方差；W为隶属度且W∈[0,1]。结合式(9)和式(10)得到稀疏系数的融合规则

XF=WAXA+(1-WA)XB

(11)

将融合后的稀疏系数XF与原字典相乘得到最终的低频融合系数

LF=XFD

(12)

3.2 改进2APCNN的高频系数融合

第一步：根据式(4)得到高频系数的改进空间频率并将作为激励输入2APCNN。

(13)

第二步：根据式(8)计算高频系数的链接强度。

(14)

第四步：直到第三步迭代停止，根据点火数映射图选择高频融合系数。

(15)

4 实验与分析

为验证算法的融合效果，选取2组已配准的多聚焦图像(Clock、Lab)进行融合,见图2。实验中图像均来自http://www.imagefusion.org/。本节实验所使用的计算机处理器为Intel(R)Core(TM)i7-4720HQ CPU@ 2.60 GHz，内存为12.0 GB，操作系统为Windows 10 64位系统，运行平台为Matlab 2016a。并将算法与其他3种算法进行了对比：(1)文献[14]提出的NSCT作为分解工具，低频系数采用稀疏表示融合策略，高频系数采用2APCNN融合策略，标记为NSCT-2APCNN。(2)屈小波等[17]提出的改进拉普拉斯能量和尖锐频率局部化Contourlet域方法，低频系数采用均值融合策略，高频系数采用SML取大策略，记为SFLCT-SML。(3)文献[18]提出的DTCWT与SR相结合，低频系数采用稀疏表示融合，高频系数采用绝对值取大融合策略，记为DTCWT-SR。参数均保持原作者所采用参数。本文算法记为M-DTCWT-2APCNN，M-DTCWT分解层数为3层，各层方向子带数目分别为[2，4，8]。

图2 Clock融合结果

Clock图像的融合结果如图2(a)～图2(d)所示。从视觉效果上来看，几种算法均实现了多聚焦图像融合，但因分解工具及融合策略的不同，融合后图像的质量也不同。为更明显地展示视觉上的差别，将各融合图像与原左聚焦图像做差得到融合结果残差如图2(e)～图2(h)所示，对于残差图像来说，更少的残差信息说明从原图像中转移了更多信息到融合图像中。从图2中可以看出(已用矩形框标出)，图2(e)、图2(f)的残差虽然不太明显，但仍然可以看出残留了闹钟顶部的大致轮廓，说明NSCT-2APCNN与SFLCT-SML这2种方法没有较好地将原图像信息融合进图像中。基于DTCWT-SR方法的残差图2(g),在闹钟轮廓上融合较好，但隐约可以辨认出时针与分针，并没有将此信息较好地融合进图像中。而本文算法得到的图2(h)几乎没有残留信息无法辨认出物体。

图3(a)～图3(d)为Lab图像的融合结果，各融合结果与原右聚焦图像的残差图显示在图3(e)～图3(h)中。可以看出在残差最明显的是NSCT-SR方法得到的融合图像，其次是SFLCT-SML与NSCT-2APCNN，但仍然可以辨认出人体轮廓残差较为明显。然而采用本文算法进行融合的残差图像中几乎没有残留信息，只在人体头部有细小痕迹。综上说明：相比较于其他3种方法，本文提出的融合算法能够更好地捕获原图像中聚焦良好区域的信息，有效提升了融合质量。

图3 Lab融合结果

为了更好评估本文算法在多聚焦图像上的融合性能，还选取了3种客观评价指标：边缘信息度量QAB/F、互信息MI和空间频率SF进行度量[19]。QAB/F衡量有多少边缘信息从原图像转移到融合后图像；MI代表原图像有多少信息转移到融合图像；而SF可以度量图像空间的总体活跃程度。对于这3个指标来说，值越大代表融合质量越高。

4.1 分解工具融合性能对比

表1为使用不同分解工具对图2(a)和图2(b)Clock图像的融合性能对比，为公平体现本文提出的多方向DTCWT分解工具对融合效果的提升，所有分解工具的低频系数均采用均值融合策略，高频系数均采用绝对值取大融合策略。

由表1可得，本文提出的M-DTCWT在所有指标中取得了最优或次优的融合效果，并于传统的DTCWT相比，在指标QAB/F、MI和SF上分别提升了3.80%、13.96%和3.81%，较其他传统算法也有一定的提升，尤其是在指标MI上较NSCT和SFLCT分别提升了14.58%和16.39%，充分体现了M-DTCWT对融合效果带来的提升，证明了其在图像融合中的应用价值。这些融合效果的提升主要归功于M-DTCWT多尺度多方向特性可以更好地对图像进行稀疏分解。运行时间上，由于加入了多方向NSDFB分解，较DTCWT提升了约1倍的时间，与SFLCT相比也提高了9.30%，NSCT则最慢，是本文算法的4.57倍。

表1 分解工具的融合性能对比

4.2 整体融合性能对比

实验通过客观评价指标QAB/F、MI、SF及运行时间Times考察不同融合方法性能的结果如表2所示。本文提出的算法在QAB/F和MI这2个指标上均取得了最大值。与SFLCT-SML算法相比较，2组图像分别提升了2.90%、15.12%和3.27%、15.48%。对采用NSCT-2APCNN算法，分别提升了1.01%、8.11%和1.41%、10.39%。相比于未改进的DTCWT-SR算法，分别提升了1.93%、8.87%和1.4%、9.18%。这主要归功于多方向DTCWT分解的多尺度多方向性、FSR的低频系数融合相关性以及改进2APCNN对高频特征的有效反应。整体上来看，本文算法对SFLCT提升最大，对NSCT-2APCNN和未改进的DTCWT-SR提升不分伯仲，但本文是对DTCWT的一种改进，因此两者的比较更具意义。

表2 综合客观评价指标

由于QAB/F和MI是一种信息转移度量且本文算法在2组实验中均取得了最大值，代表所提出方法融合了更多的原图像信息，同时这也与视觉效果对比相符合，证明了本文算法的融合效果要优于其他3种方法。在SF指标中2组实验取得最大值的分别为SFLCT-SML和NSCT-2APCNN，虽然本文算法表现较差，但与其他3种方法相比可以看出，只在小数点后第二位上略有波动，差别很小，说明未对图像的空间活跃度产生明显影响。与NSCT-2APCNN相比本文算法快了3倍、2.69倍，这是由于NSCT分解工具具有较高的冗余度因此算法运行时间较长。与SFLCT-SML相比差别较小，而对比传统的DTCWT-SR则慢了2.72倍、3倍，这主要归结于在DTCWT基础上进行了多方向NSDFB分解，增加了算法运行时间。综上所述，相比于传统方法，本文所提算法对融合效果提升较为明显，具有一定的优越性。

5 结束语

针对DTCWT在方向分解上的不足，提出了一种基于多方向双树复小波变换(M-DTCWT)的多聚焦图像融合方法。先对多聚焦图像进行M-DTCWT分解,得到低频系数与高频系数。对低频系数,提出结合模糊逻辑和稀疏表示(FSR)的融合规则得到低频融合系数。对高频系数，提出利用平均高斯差分梯度(ADOG)作为链接强度的改进双通道脉冲耦合神经网络(2APCNN)的高频融合策略。最后通过M-DTCWT的反变换得到融合图像。实验结果表明，本文算法在主观评价与客观评价上均优于传统的融合方法，较传统DTCWT方法在指标QAB/F和MI上，分别提高了1.93%、8.87%和1.40%、9.18%，体现了本文算法在多聚焦图像融合中的优越性。