单元起始课应紧扣“知识从何而来”

【摘 要】 问题情境是否合适的关键在于其设置是否有利于学生的学,以及如何让学生会学,它既要能引领整个单元的学习,还要让学生知道新知识的必要性,发生、发展的方向,探究方法等,教师在设置问题情境时,应关注其能否在大单元教学中起到一以贯之的引领作用,能否揭示数学概念的本质,特别是概念的内在逻辑结构,并关注在探究的过程中提升学生的数学能力,发展学生的学科素养.
【关键词】 单元起始课;新知识;来龙去脉
单元教学对发展学生核心素养有着重要的积极作用,我们在关注如何全局把握、整体规划单元教学时,更应该关注如何上好单元起始课,关注单元起始课应紧扣“知识从何而来”这一中心问题.《普通高中数学课程标准(2017版2020年修订)》[1]指出:在教学实践中,要不断探索和创新教学方式,不仅要重视如何教,更要重视如何学,引导学生会学数学,养成良好的学习习惯.因此从落实如何学和如何会学这一目标的角度,教师在教学实践中更应强调学习的必要性和紧要性,让学生充分了解知识的发生、发展过程,厘清数学概念的逻辑结构,从而激发学生学习动力,并促进学生有条理的自主学习与探究.
那么,如何紧扣“知识从何而来”这一中心问题呢?知识当然是从问题情境中来,更是从一个“合适”的问题情境中来.《课标》[1]明确指出:基于数学学科素养的教学活动应该把握数学的本质,创设合适的教学情境,提出合适的数学问题,引发学生的思考与交流,形成和发展数学学科素养.何谓“合适”?本文以“随机变量及其概率分布”(苏教版选修2-3)的教学设计和实录为例谈谈自己的认识.
1 教材分析与学情分析
1.1 单元教学目标
在必修课程已经学习概率的基础上,本单元将学习某些离散型随机变量的分布列及其均值、方差等内容,使学生初步学会利用离散型随机变量思想描述和分析某些随机现象的方法,并能用所学知识解决一些简单的实际问题,进一步体会概率模型的作用及运用概率思考问题的特点,使学生初步形成用随机观念观察、分析问题的意识.
1.2 目标分析解讀
通过本单元的学习,让学生学会从定量的角度来刻画离散型随机变量,这是随机观念从定性到定量的一次提升,有助于学生思维的发展.在教学实践中,通过对具体问题的分析,理解离散型随机变量及其概率分布的概念,认识分布列对于刻画随机现象的重要性,通过实例理解超几何分布及其推导过程,了解条件概率和两个事件相互独立的概念,理解n次独立重复试验的模型及二项分布,理解取有限值的离散型随机变量的均值、方差的概念等.
1.3 单元设计意图
本单元以学生熟悉的实例为背景,按照“问题情境—数学活动—意义建构—数学理论—数学应用—回顾反思”的顺序结构来展开.通过对实际问题的分析、归纳,激发学生开展活动,促使学生对现实世界中蕴涵的数学模型进行思考,进而作出理性判断,使学生能够更注重应用数学的观念、方法和语言去提炼、分析和解决问题,从而达到培养学生的创新意识和理性思维的目的,同时拉近新知识与学生的距离,提高学生的兴趣,降低学生的难度.
1.4 学情分析
学生已经掌握了古典概型的相关知识,会求简单的概率问题,在上一单元里又系统学习了排列、组合、二项式定理的相关知识,从知识层面,如何将两者融合对学生来说是陌生的;给出较为复杂的概率问题,学生受限于阅读能力和分析问题能力,很难构建新的数学模型解决问题;将问题数学化,并用数学观点进行抽象,特别是上升到变量描述问题,更是学生欠缺的能力.从能力层面,学生需要经历一个从抽象概括到数学建模以及数学应用的过程.
2 教学设计与实录
2.1 教学目标[2]
1)在对具体问题的分析中,了解随机变量、离散型随机变量的意义;
2)理解取有限值的离散型随机变量及其概率分布的概念与性质;
3)理解取离散型随机变量服从两点分布的概念;
4)认识概率分布对于刻画随机现象的重要性.
2.2 教学重难点
1)理解离散型随机变量的意义;
2)理解离散型随机变量及其概率分布的概念与性质.
2.3 教学过程
1)问题情境
问题1:在现实生活中,我们会遇到许多较为复杂的概率问题.
(1)某工厂生产的一批产品共N件,其中有M件不合格产品,在随机取出的n件产品中,尝试研究“取到不合格品数”的概率问题.
(2)语文老师要从10篇古文中随机抽3篇不同的古文让学生背诵,规定至少背出其中两篇才能过关,某位同学只能背诵出其中的6篇,他能过关的概率是多少?某同学想知道要会背诵几篇“性价比”最高?
我们可以用怎样的数学模型来刻画这些复杂的概率问题?如何运用这些数学模型解决问题?
设计意图 提出较为复杂的概率问题,让学生观察、分析,在尝试解决问题的过程中感到困难和知识的匮乏,激发新的求知欲望,提高学习动力.问题设置具有单元引领作用,又有一定的梯度,让学生在探究中获得新知识,并有目的、有方向地进行.
2)学生活动
师:情境2虽然发生在我们身边,但面对我们陌生的问题,很多同学甚至无法理解题意,情境1却让我们感到熟悉,因为在组合的学习中,我们见过类似的例子,但是为什么大家还倍感困难呢?
生1:因为N,M,n这些字母的值不能确定,甚至不合格品M与抽取产品件数n之间的大小关系也不知道,要分类讨论吧?我没有想清楚.
生2:可以特殊化,先解决简单的问题,如N=100,M=3,n=10,即:
某工厂生产的一批产品共100件,其中有3件不合格产品,在随机取出的10件产品中,尝试研究“取到不合格品数”的概率问题.
設计意图 特殊化思想是高中数学学习中的一种重要的基本思想和方法,对于分析问题、解决问题等都有着很重要的作用.从一般到特殊,降低思维要求,寻求规律方法,再从特殊到一般,将所寻规律方法升华.
师:你认为解决这个问题最应该关注什么?怎么处理?
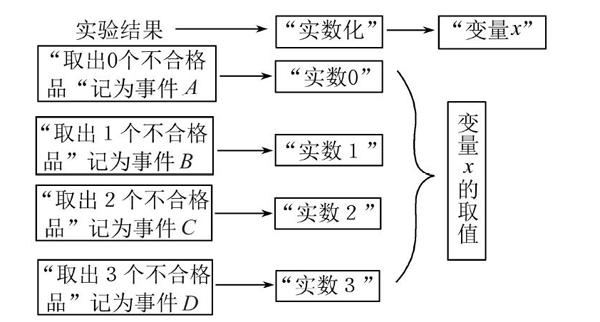
生3:取到不合格品数会有变化,可能是0个、1个、2个、3个,所以要分四种情况分别计算.
记“抽取产品,取到0个不合格品”的事件为A;
“抽取产品,取到1个不合格品”的事件为B;
“抽取产品,取到2个不合格品”的事件为C;
“抽取产品,取到3个不合格品”的事件为D,再分别计算概率.
师:很好,计算我们暂时放后处理,先来反思以上的处理过程,通过特殊化,令N=100,M=3,n=10,当然它还可以取其它值,如M=15怎么办?
生4:需要记16个事件,记到字母P后再计算概率.
师:有危机感吧?26个字母用完了怎么办?
生5:可以接着用希腊字母.(学生们在开心的大笑后陷入思考)
生6:我发现,列出的事件只有不合格品数在改变,可以用数字0、1、2、3来表示事件.这样即使事件再多也够用了.(学生们表示赞许,有了成功的喜悦)
师:将随机事件的结果与实数一一对应的做法非常有效的简化了事件的记法,同学们能否再进一步,又可以用什么刻画数的变化呢?
经过一段思考后,多位学生说出字母,变量,其他人表示认同.
教学过程如下图所示.
设计意图 学生利用已有知识解决较为复杂的问题,会遇到无法克服的障碍,教师作为教学的引导者通过问题的设疑,激发学生的求知欲,让学生经历两个重要的抽象过程,一是从具体的问题情境抽象出数字,将事件结果与实数一一对应,二是将实数抽象为字母,进行变量化,从而构建随机变量模型.
3)建构模型
定义:一般地,如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量.随机变量通常用大写拉丁字母X,Y,Z表示.也通常用小写拉丁字母ξ,η,ζ表示.
师:你能再举出一些这样的例子吗?
生7:掷骰子,出现的结果可以与数字1,2,3,4,5,6一一对应,也可以用随机变量X表示,变量X可能取值是1,2,3,4,5,6.
生8:打靶,出现的结果可以与数字0,1,2,3,4,5,6,…,10一一对应,也可以用随机变量Y表示,变量Y可能取值是0,1,2,…,10.
问题2:(1)随机抽查新生婴儿的性别,抽查的结果可能是男,也可能是女,出现的结果能否用随机变量表示?若用随机变量Z表示,则变量Z可能取值是什么?
(2) 随机抽一副扑克牌中的一张,抽的结果可能是红桃,也可能是黑桃、方片、梅花,出现的结果若用随机变量ξ表示,则变量ξ可能取值是什么?
设计意图 虽然建构了随机变量的模型,但学生的理解是狭隘的,认为只有结果是数字才可以用随机变量刻画,教师及时利用两个问题拓宽学生对概念的认识,即使结果没有数字,也可以将样本点实数化,进而用随机变量刻画.
教学过程如图所示.
2.随机抽一副扑克牌中的一张,抽的结果可能是红桃,也可能是黑桃、方片、梅花,出现的结果若用随机变量ξ表示,则变量ξ可能取值是什么?
说明:P({ξ=1})可以简记为:P(ξ=1)
4)模型应用
问题3:利用所学知识研究下列概率问题.
(1)抛掷一枚质地均匀的硬币一次;
(2)同时抛掷两枚质地均匀的硬币一次.
生9:设“抛掷硬币一次出现正面向上”为事件1,“抛掷硬币一次出现反面向上”为事件2,则随机变量X可能取值是1,2.P(X=1)=1/2,P(X=2)=1/2.
师:好的,在这个随机试验中,随机变量X是否有实际意义?能否赋予随机变量X确定的实际意义?
生10:用随机变量X表示“抛掷硬币一次,出现正面向上的次数”,则随机变量X可能取值是1,2.P(X=1)=1/2,P(X=2)=1/2.
第(2)问教学过程略.
设计意图 建构了随机变量的模型后,学生的理解依然还是狭隘的,会刻意将实验结果实数化,再刻意引入变量表示.实际上,随机变量有着重要的实际意义,而不是简单地用字母表示数,理解随机变量的实际意义有助于后续用数学工具研究概率问题的学习.
5)形成概念
给出概率分布的概念和性质,并给出两点分布或0-1分布的概念.
概率分布的定义:
一般地,假定随机变量X有n个不同的取值,它们分别是x1,x2, …,xn且P(X=xi)=pi,(i=1,2, …,n)则称之为随机变量X 的分布列,简称为X的分布列,也可以用表格表示,
Xx1x2…xn
Pp1p2…pn
此表叫概率分布表,它和分布列都叫做随机变量X 的概率分布.
性质:(1)pi≥0(i=1,2,…,n);
(2)p1+p2+ …+pn=1.
问题4:下列变量中,哪些是随机变量,哪些不是随机变量?并说明理由.
(1) 2021年4月6日南京禄口机场候机室中的旅客数量;
(2) 2021年4月6日北京至南京的航班数(正常情况下);
(3)某乘客在机场游戏厅练习投篮,投中即停止,则他停止时已投篮的次数;
(4) 2021年4月6日北京至南京CA1817次航班到达时间.
设计意图 随机变量可分为离散型随机变量和连续型随机变量,而离散型随机变量又可以分为取有限值的和取无限值的两种情况,此处安排目的是让学生作出正确的辨析.
6)课堂小结
(1)本节课你学习了哪些知识?学会了什么?有哪些新的认识?谈谈你学习过程中的重要心得体会.
(2)你认为后续还会学习哪些知识?你认为会怎样开展研究?
设计意图 在实际教学中,不仅老师要有大局观,整体规划,还要让学生也具有这样的意识,理解“知识从何处来”,又该“往何处去”,培养他们提出问题、分析问题、解决问题的能力和意识,发展学生的数学学科素养.
3 结 语
问题情境是否合适的关键在于其设置是否有利于学生的学,以及如何让学生会学,它既要能引领整个单元的学习,还要让学生知道新知识的必要性,发生、发展的方向,如何延伸、如何探究?教师在设置时,不能仅从难度、梯度上考虑,更为重要的是设置的问题情境能否揭示数学概念的本质,特别是概念的内在逻辑结构,要关注在探究的过程中怎样提升学生的数学能力,发展学生的学科素养.
参考文献
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[M].北京:人民教育出版社,2020:80-81.
[2] 石志群.高中数学教学参考书(选修2-3)配苏教版普通高中数学课程标准实验教科书[M].南京:江苏凤凰教育出版社,2012:53.
作者简介 孙秉正(1973—),男,安徽淮北人,中学高级教师,教育硕士.2005年荣获秦淮区数学学科带头人,2008年荣获南京市优秀青年教师,主要从事数学教育和教学研究,发表论文10余篇.

