车载作用下公路桥梁耦合振动精细化建模及验证分析

殷新锋 晏万里 任厚乾 刘扬

摘   要：现有车-桥耦合振动分析中车辆模型不能精确考虑车辆动力特性和柔性轮胎对车桥耦合振动响应的影响.为了进一步研究充气轮胎胎压对车-桥耦合振动的影响，基于LS-DYNA程序，采用线弹性橡胶材料模拟轮胎并定义轮胎内气压，结合常用重载三軸汽车的结构参数，运用弹簧阻尼单元及梁、壳单元模拟车辆悬架系统的动力特性，建立可分析车轮气压的三维车辆模型;并基于实桥试验结果及响应面法得到高精度有限元桥梁模型;通过显式求解程序LS-DYNA内置的接触算法，将车辆子系统和桥梁子系统联立耦合起来，形成显式的车-桥耦合振动分析模型.计算结果与实测结果对比分析验证了该方法的正确性，并分析了轮胎胎压对桥梁振动的影响.

关键词：响应面法;有限元模型修正;连续刚构桥;LS-DYNA;动力响应

中图分类号：U441.2                                        文献标志码：A

Fine Modeling of Coupled Vibration of Highway Bridge under

Vehicle Loading and Verification Analysis

YIN Xinfeng1，YAN Wanli1，REN Houqian1，LIU Yang1，2

（1. College of Civil Engineering，Changsha University of Science & Technology，Changsha 410114，China;

2. College of Civil Engineering，Hunan University of Technology，Zhuzhou 412007，China）

Abstract：In the existing coupling vibration analysis of vehicle bridge，the influence of vehicle dynamic characteristics and flexible tire on the vehicle bridge coupling vibration response can not be accurately considered. In order to further study the influence of pneumatic tire pressure on vehicle bridge coupling vibration，the linear elastic rubber material is used to simulate the tire and define the air pressure in the tire based on LS-DYNA program. Combined with the structural parameters of the commonly used heavy-duty three-axle vehicle，the dynamic characteristics of the vehicle suspension system are simulated by using the spring damping element，beam and shell element，and a three-dimensional vehicle model is established. Based on the test results of the real bridge and the response surface method，a high-precision finite element bridge model is obtained. The vehicle subsystem and the bridge subsystem are coupled together to form the explicit vehicle bridge coupling vibration analysis model through the contact algorithm built in the explicit solution program LS-DYNA. The correctness of the method is verified by comparing the calculation results with the measured results，and the influence of tire pressure on bridge vibration is analyzed.

Key words：response surface method;finite element model updating;continuous rigid-frame bridge;LS-DYNA;dynamic response

车辆在桥梁上行驶时产生的激励导致车辆和桥梁产生相互振动，该振动称为车桥耦合振动[1]. 国内外学者对车桥耦合振动问题进行了大量研究，并取得非凡成果.夏禾[2]将车辆简化为悬挂振动模型，研究了车-桥-墩相互作用的动力响应. Cai等[3-4]采用两轴车辆模型，基于功率谱密度函数生成随机桥面不平整度，分析了车辆荷载作用下桥梁振动响应. Huang等[5]采用三轴车辆有限元模型研究了简支梁的车桥随机振动. 韩万水等[6]结合实测数据对桥梁模型进行修正以得到桥梁基准模型，并采用梁格法对车桥振动进行分析. 李奇等[7]考虑车体柔性的影响，分析了高速列车和简支梁桥相互作用的影响. 邓露等[8]运用动态称重技术（BWIM）实时监测车辆总重和轴重，进行中小型跨径混凝土梁桥的振动研究.赵越等[9]基于等参映射与改进折半法在传统车桥耦合分析的基础上进一步提升其分析精度及计算效率，从而进行公路车桥耦合分析.但关于充气轮胎胎压对车-桥耦合振动影响的研究较少.主要原因为现有车-桥耦合振动分析中车辆模型多为简化的质量-弹簧-阻尼多自由度振动模型[10-13]，该模型常将车轮简化为点或者等效线面接触，故不能精确考虑车辆动力特性和柔性轮胎对车桥耦合振动响应的影响.因此，建立精确车辆模型和桥梁模型是至关重要的，这样才能提高数值模拟精度，为桥梁结构的健康运营提供有利建议.

本文以一座连续刚构箱梁桥为工程背景.首先，基于LS-DYNA程序以车辆实际构造及动力特性为基准，建立车辆精细三维有限元模型;然后，结合响应面法并依据实桥试验结果对桥梁模型进行修正，以得高精度的桥梁有限元模型;最后，通过LS-DYNA程序将桥梁模型和车辆模型进行耦合，求解车桥的振动响应，并通过改变车轮气压，分析该参数对桥梁振动响应的影响.

1   车辆模型的建立及校验

1.1   车辆模型的建立

在车桥耦合振动模型中，影响桥梁振动响应的主要因素为车辆模型的动力特性和荷载分布. 车辆模型需着重模拟悬架系统、车轮和轴重. 本文参照东风牌三轴载重自卸货车，建立车辆有限元模型，其相关参数如表1所示.前中轴距为3.5 m，中后轴距为1.4 m，后轮距为1.8 m. 基于CAD软件SolidWorks分别建立各部位的几何模型并进行网格划分，最后使用梁、壳、实体单元及离散单元等赋予不同部位网格不同的属性，从而构建车辆模型，如图1所示.

车轮由轮胎、轮盘和轮毂组成.轮胎采用线弹性橡胶材料，轮盘和轮毂采用线弹性钢材材料，车轮模型中各部位连接均为刚性连接，邊界为刚性固态约束，有限元模型如图2所示. 根据轮胎内实际气压，使用LS-DYNA程序关键字*AIRBAG_SIMPLE_AIRBAG_MODEL定义由轮胎、轮毂组成的封闭体内的气压，其气体压力值为0.6 MPa.

由于车辆悬架系统结构复杂，本文采用壳单元、刚体、弹簧阻尼单元和多点约束来模拟悬架系统.前后悬架的弹簧和阻尼器的参数参考文献[14]，前悬架的弹簧刚度取800 N/mm，阻尼系数取20 Ns/mm;后悬架的弹簧刚度取1 200 N/mm，阻尼系数取25 Ns/mm. 前后悬架实体构造及有限元模型如图3所示.

为了使车轮正常转动，在轮盘与车轴之间设置旋转铰，再通过定义*INITIAL_VELOCTIY_GENERATION关键字设置车轮的转动和平动速度，实现车轮滚动向前的状态，如图4所示.

1.2   车辆模型的校验

在车辆模型的3个轴上选择6个节点，约束竖向位移. 然后对车辆施加重力荷载使车辆产生瞬时振动，再通过定义关键字*DAMPING_GLOBAL对车辆模型施加全局阻尼，使其快速达到稳定状态，计算出约束反力，并与实测车辆轴重进行比较，最终得到车辆模型的轴载曲线如图5所示.

由表2知，车体总重偏差为0.87%，说明实测车辆轴重分布特性能体现于建立的车辆模型.

通过对比车辆模型和实测车辆的自振频率，验证车辆模型动力特性的有效性. 如图6所示，该车实测自振频率为1.635 Hz，车辆有限元模型的自振频率为1.647 Hz，显然，两者基频相差很小.

2   桥梁模型

2.1   桥梁概况

该桥主桥为三跨变截面预应力混凝土连续刚构结构，跨径布置为（65+120+65） m，其立面及断面示意图分别如图7和图8所示.

2.2   实桥试验

利用有限元软件ANSYS建立初始有限元模型如图9所示. 主梁和墩身都用实体单元模拟，墩底采用固结连接. 混凝土密度取为2 500 kg/m3，主梁和墩的混凝土弹性模量分别为34.5 GPa和32.5 GPa.

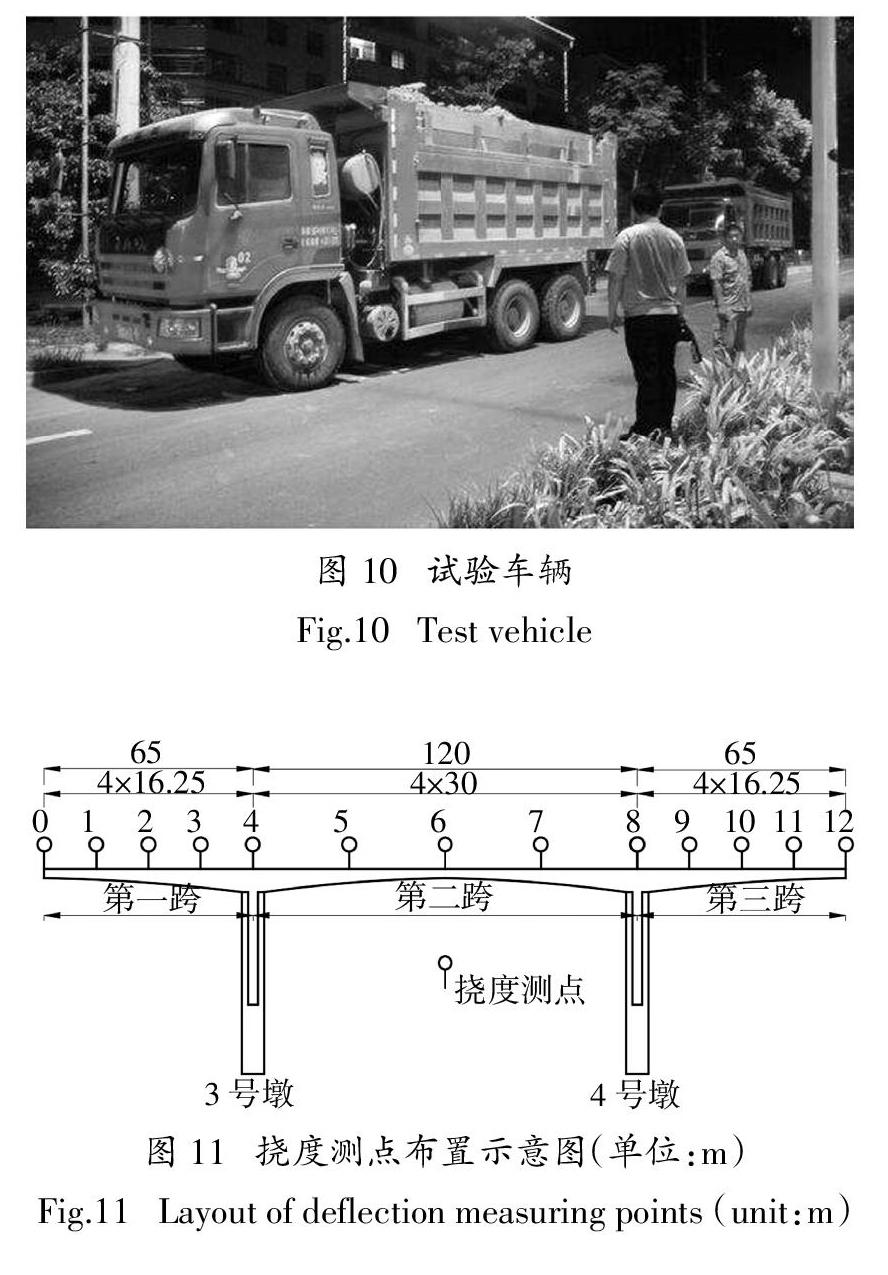
现场对桥梁进行静力试验，测试中加载车辆总数为6辆，每辆总重为35 t，车辆前轴重7 t，中轴和后轴各重14 t，车辆照片如图10所示.

在正式试验前先进行预加载，以消除非弹性变形，确保试验及设备处于良好工作状态. 正式试验中将加载车分3级加载，每一级加载持荷2 ～ 3 min，待实测应变及挠度数据稳定后进行数据的采集工作，再进行下一级的加载工作. 限于篇幅，仅就其中一个工况做详要概述. 为了使加载截面承受最大正弯矩，在中跨跨中截面中心加载，相应的荷载效率系数为0.967.挠度测点布置如图11所示.

实桥试验的挠度采用水准仪进行测量，现场测试照片如图12所示.脉动试验采用多通道数据采集分析系统NI公司的PXI系统进行试验，采用8330B3型超低频加速度传感器进行数据采集，最低采样频率从0 Hz开始，采集主梁横向和竖向振动数据，再经信号分析得到全桥的各阶固有振动特性，现场采集照片如图13所示.

2.3   基于响应面法的有限元模型更新

基于响应面法的有限元模型修正是用响应面函数来模拟实际结构的响应函数，将试验设计与数理统计相结合，通过样本选取、方差分析参数选取、响应面的拟合及采用优化算法寻求响应面模型中的最优解来进行有限元模型修正.

据文献[15-16]知，影响有限元模型与实测桥梁结构差别的主要因素为结构混凝土密度、主梁和墩混凝土弹性模量，因此取这三个因素作为变量. 为获得响应与所选定的三参数之间的联系，首先需要参数设计. 根据参数取值的变化规律，假设三参数的单位长度值为10%，则可得该三参数值的变化范围见表3.

以桥梁模态和静力变形为目标来更新桥梁模型，选取桥梁结构的第一阶自振频率（R1）、测点5挠度值（R2）和测点6挠度值（R3）作为目标函数.这3个目标函数充分利用了现场的实桥试验条件，且包含了桥梁静、动力性能指标，可较为全面、准确地反映桥梁的力学性能.

根据上述试验设计，应用回归分析技术对样本数据进行响应面拟合，并用R2准则和R2adj准则进行响应面拟合精度的检验，其表达式见方程（1）（2）.

式中：SST = SSE + SSR表示模型的总方差;dT表示模型的总自由度.如果R2和R2adj的值都接近1且两者差值很小，则表示响应面方程拟合得很好.

采用二次多项式对上述样本结果进行响应面拟合，并用R2和R2adj准则对响应面的精度进行检验，检验结果如表4所示.

从表4知，R2和R2adj值均接近1，且两者差值很小，说明模型拟合精度较高，能很好地表示各参数与目标函数的关系.

响应面函数采取省略交差项影响的二次多项式，则响应面拟合方程如方程（3）～（5）所示：

R1 = 0.821 9 - 0.000 3X1 + 0.012 7X2 +

0.012 0X3 - 0.000 1X22 - 0.000 1X23       （3）

R2 = 9.764 8 + 0.005 0X1 - 0.632 7X2 +

0.067 9X3 + 0.008 7X22 - 0.001 5X23       （4）

R3 = 16.557 2 + 0.008 6X1 - 1.050 3X2 +

0.091 6X3 + 0.014 4X22 - 0.002 3X23       （5）

该桥的第一阶实测频率为0.867 Hz;实桥跨中试验加载的情形下，测点5、6的挠度值分别为5.687 mm和9.679 mm. 根据实测值和数值模拟值可以建立一个目标函数：

式中：R（i）为根据响应面法计算的响应;M（i）为实测值;coef（i）为权重系数，此处取为[1.5 1 1].目标函数可以利用Matlab中的遗传算法（Genetic Algorithm）工具箱优化.更新后的上述三参数分别如表5所示.

从表5可得，主梁和墩的混凝土弹性模量和密度都有所增加，说明依托工程的施工质量较为可靠，同时参数的变动范围仍在工程实践的常见范围之内，说明了修正结构的可靠性.利用所更新的参数计算得到大桥的第一阶振动频率及上述工况的试验加载测点挠度如表6所示.

3   振动响应对比分析

3.1   现场测点布置及荷载工况

该连续刚构桥主要对主箱梁在如图14所示截面1、2处（即边跨跨中、中跨跨中）的动位移与应变变化情况进行了分析，全桥共计布设动位移测点5个，应变测点18个.

现场布置了3种荷载工况：工况1，一辆35 t重车置于桥纵向中轴线上;工况2，两辆35 t重车并排对称置于桥纵向中轴线两侧，两车横向间距为1.3 m;工况3，四辆35 t重车以桥纵向中轴线对称放置，车辆横向间距为1.3 m，纵向间距为4 m. 所有工况，车辆均以40 km/h的速度从桥外驶入并通过桥梁.限于篇幅，仅列出工况3的车辆布置图，如图15所示.

3.2   结果对比分析

3.2.1   动位移对比

将上述各个工况进行对比分析，边/中跨跨中的位移实测值与计算值对比如图16和图17所示.

由图16和图17可知，计算值与实测值随时间变化的波动规律一致，但存在同一时刻计算值与实测值吻合不是很好的情况，且计算值的曲线波峰稍大于实测值，两者静态竖向位移差值在1.71%～6.55%之间，振动位移（消除静态位移值）幅值差值在3.71%～6.35%之间.其误差主要原因可能是：1）桥梁模型虽经过合理的参数更新，但与实测桥梁结构特性还有一定差别;2）实桥试验受车辆速度控制、行驶轨迹、仪器误差等因素的影响，测量数据精度有较大的误差.

3.2.2   动应变对比

将上述各个工况进行对比分析，边、中跨跨中的动应变实测值与计算值对比如图18和图19所示.

由图18和图19可知，计算值与实测值两者的变化规律一致，且数值模拟结果与实测数据吻合得较好.但计算值的曲线波峰稍大于实测值，两者动应变的差值在3.35%～6.94%之间，振动应变（消除静态应变值）幅值差值在2.83%～5.96%.

从上述对比情况可知，竖向振动位移与动应变的计算值与实测值随时间的变化趋势一致，且整体吻合较好，峰值接近，说明该法建立的桥梁模型和车辆模型是有效的，能应用于车桥耦合计算中.

4   轮胎气压对桥梁振动的影响

轮胎气压的大小与轮胎变形成几何关系，因此，轮胎气压对跨中振动响应影响反映了轮胎变形对梁跨中振动的影响.以上述工况2为例，取3种分别为P1=0.4 MPa、P2=0.6 MPa、P3=0.8 MPa的不同气压，来分析车轮气压变化对中跨跨中动位移和动应变的影响.

从图20和图21可得，当车轮气压由0.6 MPa减少到0.4 MPa时，车轮柔性变大，与桥面的接触面增大，桥梁中跨跨中动位移峰值减小3.6%，動应变减小2.7%;当车轮气压由0.6 MPa增加到0.8 MPa时，车轮刚度变大，与桥面的接触面减少，桥梁中跨跨中动位移峰值增大4.4%，动应变增大3.85%.

5   结   论

本文基于LS-DYNA程序建立了车-桥相互作用模型.设立多种荷载工况，通过计算值与实测值的对比，验证了车辆模型的有效性及该法建立车桥耦合模型的可行性，并进一步分析了车轮气压变化对车桥振动的影响.结果表明：1）本文方法可较真实再现车-桥耦合振动情形，无需自编复杂的车桥耦合分析程序，只需定义LS-DYNA软件自带的面面接触关键字，就可以实现车桥间的耦合作用;2）可方便获得桥梁任意部位的应力、应变及其他响应数据;3）可高精度分析车轮气压变化及车辆其他参数对耦合系统振动影响.

参考文献

[1]    殷新锋. 汽车荷载作用下梁式桥与斜拉桥的动态响应分析[D].长沙：湖南大学，2010：6—20.

YIN X F. Dynamic response analysis of girder bridge and cable-stayed bridge under vehicle load [D]. Changsha：Hunan University，2010：6—20. （In Chinese）

[2]    夏禾. 车辆与结构动力相互作用[M]. 北京：科学出版社，2005：154—164.

XIA H. Vehicle-structure interaction [M]. Beijing：Science Press，2005：154—164. （In Chinese）

[3]    CHEN S R，CAI C S. Accident assessment of vehicles on long-span bridges inwindy environments[J]. Journal of Wind Engineering and Industrial Aerodynamics，2004，92（12）：991—1024.

[4]    CAI C S，SHI X M，ARAUJO M. Effect of approach span condition on vehicle-induced dynamic response [J]. ASCE Journal of Bride Engineering，2007，14（4）：440—449.

[5]    HUANG D Z，WANG T L. Impact analysis of cable-stayed bridges[J]. Computers and Structures，1992，43（5）：897—908.

[6]    韩万水，王涛，李永庆，等. 基于模型修正梁格法的车桥耦合振动分析系统[J]. 中国公路学报，2011，24（5）：47—55.

HAN W S，WANG T，LI Y Q，et al. Analysis system of vehicle-bridge coupling vibration with grillage method based on model updating[J]. China Journal of Highway and Transport，2011，24（5）：47—55. （In Chinese）

[7]    李奇，吳定俊，邵长宇. 考虑车体柔性的车桥耦合系统建模与分析方法[J]. 振动工程学报，2011，24（1）：41—47.

LI Q，WU D J，SHAO C Y. Modeling and dynamic analysis method of vehicle-bridge coupling system considering car-body flexibility[J]. Journal of Vibration Engineering，2011，24（1）：41—47. （In Chinese）

[8]    邓露，李树征，淡丹辉，等. 桥梁动态称重技术在中小跨径混凝土梁桥上的适用性研究[J]. 湖南大学学报（自然科学版），2020，47（3）：89—96.

DENG L，LI S Z，DAN D H，et al. Study on applicability of bridge weigh-in-motion technology in short-to medium-span concrete girder bridges[J].Journal of Hunan University （Natural Sciences），2020，47（3）：89—96. （In Chinese）

[9]    赵越，黄平明，刘修平，等. 基于等参映射与改进折半法的公路车桥耦合分析系统[J]. 湖南大学学报（自然科学版），2020，47（11）：29—37.

ZHAO Y，HUANG P M，LIU X P，et al. Highway vehicle-bridge interaction analysis system based on isoparametric mapping and improved binary search [J]. Journal of Hunan University （Natural Sciences），2020，47 （11）：29—37. （In Chinese）

[10]  李小珍，刘德军，晋智斌. 大跨度铁路悬索桥车-线-桥耦合振动分析[J]. 钢结构，2010，25（12）：6—12.

LI X Z，LIU D J，JIN Z B. Analysis of train-track-bridge coupled vibration of a railway long-span suspension bridge[J]. Steel Construction，2010，25（12）：6—12. （In Chinese）

[11]  朱志辉，王力东，龚威，等. 多种垂向轮轨关系的对比及改进的车-线-桥系统迭代模型的建立[J].中南大学学报（自然科学版），2017，48（6）：1585—1593.

ZHU Z H，WANG L D，GONG W，et al. Comparative analysis of several types of vertical wheel/rail relationship and construction of an improved iteration model for train-track-bridge system[J]. Journal of Central South University （Science and Technology），2017，48（6）：1585—1593.（In Chinese）

[12]  譚国金，刘寒冰，程永春，等. 基于车-桥耦合振动的简支梁桥冲击效应[J]. 吉林大学学报（工学版），2011，41（1）：62—67.

TAN G J，LIU H B，CHENG Y C，et al. Analysis of impact of vehicle to simply supported beam bridge based on vehicle-bridge coupled vibration[J]. Journal of Jilin University （Engineering and Technology Edition），2011，41（1）：62—67. （In Chinese）

[13]  李岩，吴志文，蔡明，等. 一种随机车流与桥梁耦合振动的分析方法[J]. 哈尔滨工业大学学报，2018，50（3）：46—52.

LI Y，WU Z W，CAI M，et al. An analysis method for coupled vibration random traffic flow and bridge[J]. Journal of Harbin Institute of Technology，2018，50（3）：46—52. （In Chinese）

[14]  陈水生，赵辉，桂水荣，等. 基于LS -DYNA公路桥车桥耦合的车辆模型研究[J]. 计算力学学报，2019，36（6）：747—756.

CHEN S S，ZHAO H，GUI S R，et al. Vehicle model research on vehicle bridge coupling of highway bridge based on LS -DYNA[J]. Chinese Journal of Computational Mechanics，2019，36（6）：747—756. （In Chinese）

[15]  DENG L. System identification of bridge and vehicle based on their coupled vibration[D]. Baton Rouge：Louisiana State University，2009：7—23.

[16]  YIN X F，FANG Z，CAI C S，et al. Non-stationary random vibration of bridges under vehicles with variable speed[J]. Engineering Structures，2010，32（8）：2166—2174.