锈损冷弯薄壁C形钢轴压短柱试验研究

徐善华 孙建设 聂彪

摘   要：研究了锈蚀对冷弯薄壁C形钢轴压短柱承载性能的影响. 通过板材单调拉伸试验，研究了锈损冷弯薄壁钢板材的力学性能退化规律;通过对5根锈损C形钢短柱进行轴压试验，分析了其破坏模式、变形特征和承载力，并讨论了锈损C形钢轴压短柱极限荷载的计算方法. 研究结果表明：锈损板材屈服平台变短甚至消失，屈服强度随锈蚀率的增大呈线性下降趋势;锈损C形钢轴压短柱的破坏模式为腹板局部屈曲，局部屈曲多发生在腹板最薄弱处;极限荷载随着平均厚度损失率的增大呈线性下降趋势;考虑钢材力学性能退化并利用厚度折减修正的有效宽度法和直接强度法均能较好地预估锈损C形钢轴压短柱的极限荷载，但修正后的直接强度法更接近试验结果，修正后的有效宽度法则偏于保守.

关键词：锈损;冷弯薄壁C形钢;轴压;短柱;极限荷载

中图分类号：TU392.1;TU317.1                   文獻标志码：A

Experimental Investigation on Corroded Cold-formed Thin-walled

C-shaped Steels Short Columns under Axial Compression

XU Shanhua1，SUN Jianshe1，2，NIE Biao1

（1. School of Civil Engineering，Xian University of Architecture and Technology，Xian 710055，China;

2. Shandong Province Metallurgical Engineering Co Ltd，Jinan 250101，China）

Abstract：This paper studies the influence of corrosion on the bearing capacity of cold-formed thin-walled C-shaped steel short columns under axial compression. Through the monotonic tensile test of the plate，the mechanical property degradation law of the corroded cold-formed thin-walled steel plate was studied. Five corroded cold-formed thin-walled columns were subjected to axial compression test. Failure mode，deformation characteristics and bearing capacity of the columns were analyzed. The calculation method of the ultimate load was discussed. The experimental results show that the yield platform of corroded steel becomes shorter or even disappears，and its yield strength decreases linearly with the increase of corrosion rates. The failure mode of the corroded C-shaped short column under axial compression is local buckling failure of the web，but local buckling occurs mostly at the weakest part of the web. The ultimate load decreases linearly with the increase of the average thickness loss rate. The effective width method and the direct strength method，considering the degradation of the mechanical properties of the corroded steel and thickness reduction，can predict the ultimate load of the C-shaped steel short columns under axial compression. However，the modified direct strength method is closer to the test results，and the modified effective width method is more conservative.

Key words：corrosion;cold-formed thin-walled C-shaped steel;axial compression;short column;ultimate load

相比热轧钢，冷弯薄壁型钢具有轻质高强、抗震性能好、截面设计灵活、受力合理且易于工业化等优点而被广泛应用[1].  但因其多为开口截面且壁厚较薄、板件宽厚比较大，稳定性问题更为突出，因此对冷弯薄壁型钢的研究主要集中在稳定性和屈曲理论等方面[2-3]. 长期暴露在工业环境中的钢材不可避免地产生一定程度的锈蚀，锈蚀不仅导致钢材截面面积损失和材料性能退化，而且降低结构的承载性能[4-7].

目前，关于锈损钢材力学性能和锈损钢构件承载性能的研究已获得较多成果. 张世骥等对锈损Q235钢板进行拉伸试验，发现锈蚀对钢板的抗拉强度、屈服强度均有影响[8]. 徐善华等指出锈蚀导致冷弯薄壁型钢材料强度和延性发生退化，且点蚀对延性的影响高于全面锈蚀，锈蚀对冷弯薄壁型钢材料性能的影响高于热轧型钢[9-10];讨论了锈损H型钢偏心受压柱的整体稳定承载性能参数随锈蚀率的变化趋势，分析了锈蚀导致偏心受压钢柱承载性能发生劣化的原因[11].  Karagah等对局部锈损H型钢柱进行轴压试验，得出翼缘锈蚀对承载力的影响比腹板锈蚀更显著[12]. 徐善华等通过低周往复荷载试验，研究了锈损H型钢柱的侧向承载力和耗能能力，发现翼缘锈损钢柱的耗能能力迅速下降[13]. Beaulieu等研究了锈蚀对角钢抗压承载力的影响[14]. 史炜洲等发现截面损失是影响锈损焊接H型钢梁承载性能的主要因素，翼缘或腹板锈蚀越严重，承载力越低[15]. Sharifi等研究了锈损钢梁剩余弯矩的计算方法，并给出了厚度损失和剩余弯矩之间的定量关系[16]. 聂彪等发现锈损钢梁的截面模量、名义屈服强度和极限承载力随锈蚀时间的延长逐渐降低，并且锈损钢梁的可靠指标或失效概率会急剧恶化[17]. Wang等分析了锈蚀对焊接钢节点抗震性能的影响，焊接区的锈坑加剧了梁翼缘的脆性断裂破坏，导致焊接钢节点的延性和耗能能力显著降低[18].  Cascini等发现由于冷弯薄壁型钢壁厚较薄可能会加剧锈蚀的危险性，且锈蚀与屈曲之间的耦合作用会显著地降低结构的承载能力[19]. 锈损钢构件的研究主要针对热轧钢，而冷弯薄壁型钢经过冷加工，其力学性能与热轧钢存在明显不同，但是目前对锈损冷弯薄壁型钢构件的研究鲜有报道. 因此，锈损冷弯薄壁型钢构件的承载性能是亟待解决的问题.

本文主要研究了锈蚀对冷弯薄壁C形钢轴压短柱承载性能的影响，通过板材单调拉伸试验，研究了锈损钢材力学性能的退化规律;通过对5根锈损C形钢短柱进行轴压试验，分析了锈蚀对轴压短柱的破坏模式、变形特征、临界屈曲荷载和极限荷载的影响，并讨论了极限荷载的计算方法.

1   试验方案

1.1   材性试验

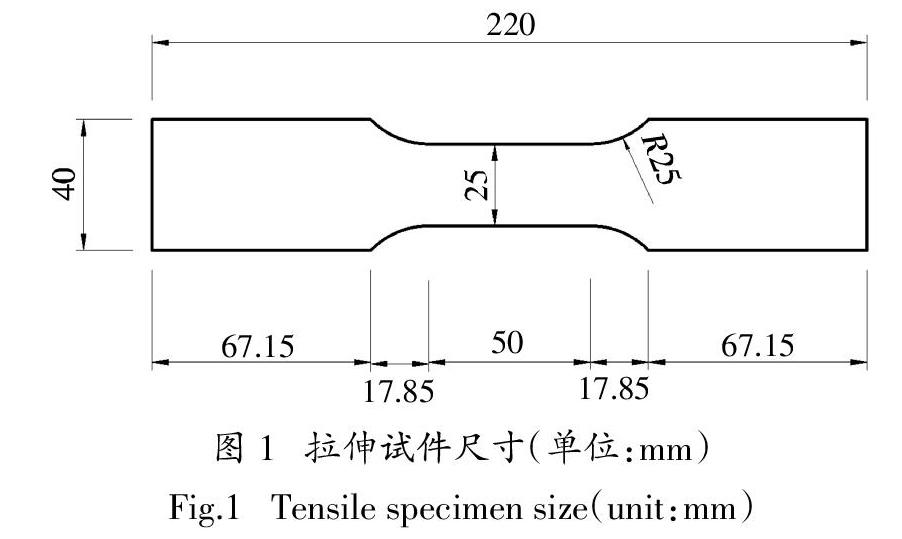
试件取自某工业厂房服役9年的冷弯薄壁C形钢檩条，原始截面尺寸为C200 mm × 65 mm × 15 mm × 2.5 mm，钢材强度等级为Q235. 从每根锈损C形钢的腹板中间部位线切割得到拉伸试件，如图1所示. 试件除锈后采用超声波测厚仪测量标距段内5个截面的厚度，各截面取5个测点，然后对各截面厚度取均值，并将5个截面均值中的最小值定义为最小厚度d. 试验装置采用DNS300型号电子万能试验机，按照文献[20]的要求进行单调拉伸试验，试件屈服前加载速率取为0.75 mm/min，屈服后加载速率取为5 mm/min.

拉伸试件的锈蚀率采用截面损失率η表征，按式（1）计算：

式中：d0为试件原始厚度（d0=2.5 mm）;d为最小厚度.

拉伸试件的应力-应变曲线如图2所示，主要表现为弹性阶段变短、屈服点下降、屈服平台变短甚至消失，仅AC1和AC3存在屈服平台. 表1给出了材性试验的力学性能参数，其中da为试件平均厚度，Es为弹性模量，fy为屈服强度（统一取残余应变为0.2%时的应力），fu为极限强度. 从表1可看出随着截面损失率的增大，钢材屈服强度显著降低，但极限强度降幅不大. 屈服强度fy与截面损失率η的拟合曲线如图3所示，fy随着η的增大呈线性下降趋势，其关系为式（2）.

fy = 280.02 - 473.88η        （2）

锈损试件表面粗糙不平，较薄处应力发展较快，导致截面应力分布不均匀是钢材力学性能退化的主要原因. 其次冷加工改变了钢材的力学性能，虽提高了钢材的强度，但同时降低了钢材的延性，使其力学性能更易受到锈蚀的影响.

1.2   试件设计

为消除整体屈曲的影响，短柱的长度不宜过长，但也不宜过短以免支座约束板件局部屈曲. 参考美国结构稳定研究文员会的建议[21]，短柱的长度L应符合式（3）要求：

3bmax ≤ L ≤ 20imin        （3）

式中：bmax为板件的最大宽度;imin为截面主轴的最小回转半径.

为保证试件在加载过程中均匀受力，在试件两端焊接尺寸为240 mm × 110 mm × 10 mm的端板. 试验前对试件截面尺寸进行测量，取4个测点的平均值，测量结果见表2. 表中符号定义如图4所示，其中L为试件长度，A为截面面积，h为腹板高度，b1、b2为翼缘宽度，a1、a2为卷边宽度.

1.3   厚度测量

锈损试件厚度的不均匀变化对轴压试件的屈曲位置和承载性能影响较大，因此需对试件进行厚度测量. 将试件沿长度方向均匀分成14个截面，同一截面取11个测点（腹板5个测点、两侧翼缘各2个测点、两侧卷边各1个测点），然后采用精确度0.01 mm的超声波测厚仪测量各测点的厚度. 试件厚度测量结果见表3，其中ta为试件平均厚度，ηa为试件平均厚度损失率，Cv为厚度变异系数.

试件的锈蚀损伤指标采用平均厚度损失率ηa表征，ηa按式（4）计算：

式中：t0为未锈损试件原始厚度（t0 = 2.5 mm）.

Cv可体现出锈蚀后试件厚度的离散程度及锈蚀的不均匀程度，按式（5）计算，由表3可知随着ηa的增大，Cv逐渐增加.

式中：σ為厚度测量结果的标准差.

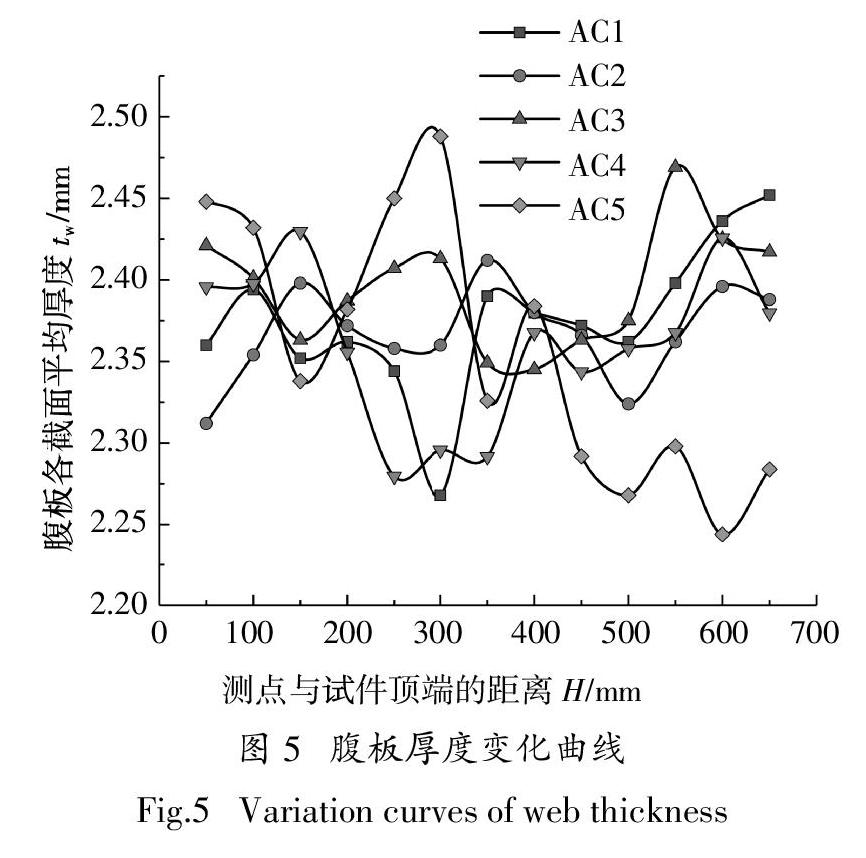
图5给出了腹板厚度沿试件长度方向的变化曲线，其中tw为腹板各截面5个测点的平均厚度，将tw最小值所对应的截面定义为腹板最薄弱处.

1.4   测点布置

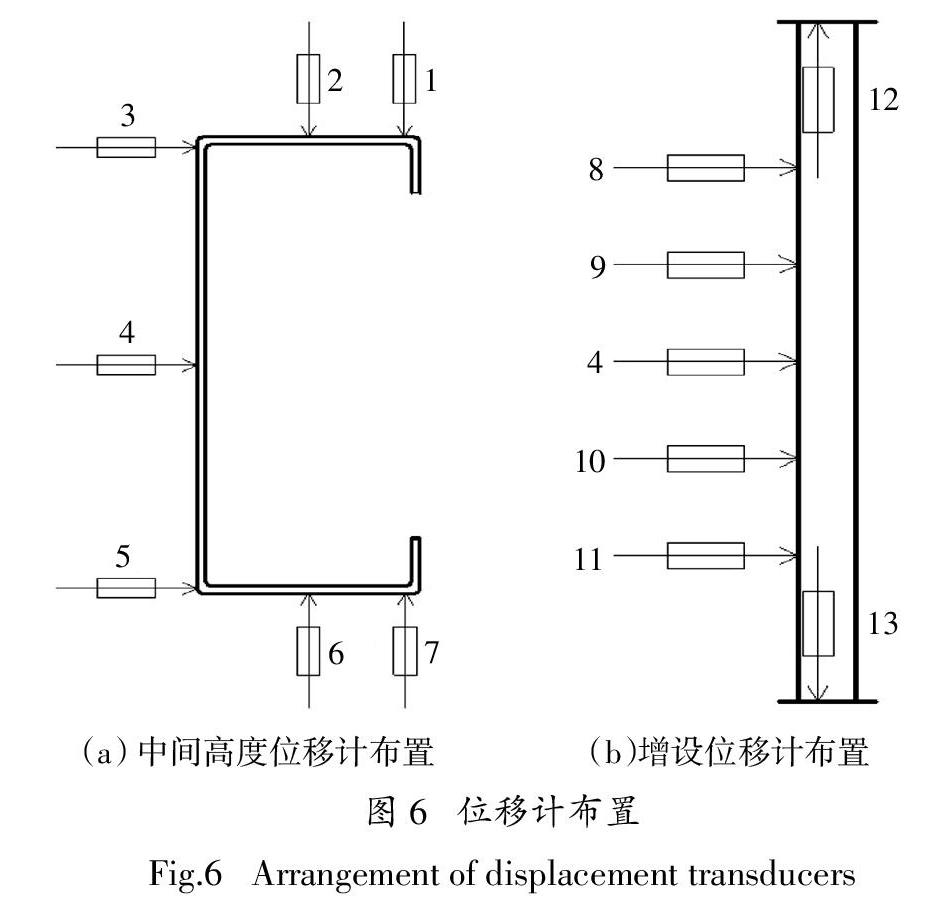
侧向位移计主要布置在中间高度处，如图6（a）所示. 由于锈蚀的随机性，锈损C形钢短柱屈曲位置不易确定，为反映试件可能发生的局部屈曲变形，在腹板中心线处增设4个侧向位移计，如图6（b）所示. 为测量试件的轴向压缩位移，上下端板形心各布置一个轴向位移计，编号分别为12和13.

为获得试件不同高度处的应力分布，除在试件中间截面处布置应变片外，另在距试件中间截面上下间隔100 mm和200 mm处增设4组应变片. 所有应变片均在C形钢内外侧对称布置，应变片具体布置及编号如图7所示.

1.5   加载方案

试验采用单刀铰支座，加载装置如图8所示. 试件安装时先进行几何对中，然后加载至0.15 ～ 0.5倍预估极限荷载，当试件4个角部应变的最大与最小值之比不超过1.15时，物理对中满足要求. 对中结束后，卸载至1 kN，然后开始正式逐级加载. 每级荷载不超过预估极限荷载的5%，当出现局部失稳或达到预估极限荷载的80%后，荷载增量取值减小. 试验进入卸载阶段，进行卸载曲线的测量，当荷载降至极限荷载的80%时，试验结束.

2   试验结果分析

2.1   试验现象

图9给出了试件的破坏模式. 随着荷载的增加，腹板沿试件纵向出现3 ～ 4个半波的局部屈曲，半波长度约等于腹板宽度. 当加载接近极限荷载时，腹板最薄弱处局部屈曲明显，最终破坏模式为腹板局部屈曲. 在极限荷载之前，翼缘和卷边变形不明显;达到极限荷载之后，翼缘有轻微侧向位移.

由图9可知不同锈蚀程度试件的破坏模式均为腹板局部屈曲，但锈蚀会影响试件的屈曲位置，多数试件在腹板最薄弱处破坏. 其中AC1、AC2、AC3和AC4在腹板最薄弱处附近破坏，AC5在腹板局部初始缺陷最大处破坏.

2.2   荷载-应变（位移）曲线

2.2.1   荷载-轴向位移曲线

试验荷载-轴向位移曲线如图10所示. 加载初期，荷载随位移的增加呈线性增长，加载至约极限荷载的80%时，曲线斜率显著降低. 在曲线下降段，随着锈蚀率增大，荷载下降速率逐渐增加，表明试件锈蚀后塑性变形能力降低，延性变差.

2.2.2   荷载-侧向位移曲线

腹板典型的荷载-侧向位移曲线如图11所示，侧向位移以内凹为负、外凸为正. 从图11可看出部分曲线的侧向位移出现正值，主要原因是随着荷载的增加，腹板沿试件纵向出现多个局部屈曲半波，达到极限荷载后，侧向位移均变为负值.

为研究锈蚀对侧向位移发展的影响，图12给出了破坏位置处腹板的荷载-侧向位移曲线. 由图12可知随着锈蚀率的增大，侧向位移的增长速率逐渐增加，主要原因是试件锈蚀越严重，腹板宽厚比越大，翼缘对腹板的约束作用降低，局部屈曲越容易发生，变形增长速率也逐渐增加. 另外随着锈蚀率的增大，达到极限荷载时所对应的侧向位移逐渐增大，说明屈曲后变形发展较充分.

2.2.3   荷载-应变曲线

腹板典型的荷载-应变曲线如图13、图14所示，拉应变为正，压应变为负. 从图可看出腹板中心线处内外侧对称应变差别较大，且在加载后期因发生局部屈曲，应变差值逐渐增大并出现应变反向现象.

为研究锈蚀对应变发展的影响，图15给出了腹板与翼缘相交处的荷载-应变曲线，曲线横坐标分别取E5与F5的应变均值、E7与F7的应变均值. 由图15可知随著锈蚀率增大，应变的增长速率逐渐增加，主要原因是试件锈蚀后截面面积减小.

限于篇幅，文中仅给出了腹板典型的荷载-应变曲线及荷载-侧向位移曲线. 翼缘和卷边内外侧应变差别较小，且在极限荷载之前未出现拉应变;翼缘的侧向位移在达到极限荷载之前均小于1.5 mm，且在试验过程中无明显畸变.

2.3   承载性能退化结果

表4给出了锈损轴压短柱的力学性能参数，其中ηa为试件平均厚度损失率;Cv为厚度变异系数;Δtu为极限位移;Ptu为极限荷载;Ptcr为临界屈曲荷载;σu为极限应力，按σu = Ptu/A计算，A为截面面积.

由表4可知极限位移Δtu和极限应力σu均随着平均厚度损失率ηa的增大而逐渐降低，说明锈蚀导致试件提前破坏，钢材强度得不到充分发挥. 主要原因是锈蚀导致试件表面粗糙不平，厚度较薄处局部应力较大，当局部应力达到一定水平后试件即发生破坏，剩余截面的强度无法充分发展.

极限荷载Ptu随着ηa的增大显著降低，当ηa从 4.74%增加至8.32%时，Ptu下降了18.37%. 图16为Ptu的退化曲线，可看出Ptu随着ηa的增大呈线性下降趋势，下降速率k1 = 660.95. 极限荷载下降如此之快的主要原因是锈蚀导致试件截面损失和钢材力学性能下降.

临界屈曲荷载Ptcr根据应变反向准则确定[22]，例：图14（a）中N2的最大压应变所对应的荷载即为Ptcr. Ptcr变化幅度较大，约为P tu的0.25 ～ 0.55倍，其与腹板的宽厚比和初始缺陷密切相关. 腹板局部初始缺陷越大，则该位置更易发生屈曲;锈蚀越严重，试件越薄，腹板宽厚比越大，则临界屈曲应力越低.

试件的理论临界屈曲荷载Pccr = σcr A，A为截面面积，σcr 为腹板（按四边简支的均匀受压板考虑）的弹性临界屈曲应力，按式（6）计算，式中泊松比取v = 0.3，弹性模量取Es = 1.85 × 105 MPa，腹板的弹性稳定系数取kw = 4.

由式（6）可知，锈蚀越严重，腹板宽厚比b/ta越大，则弹性临界屈曲应力σcr越低，临界屈曲荷载降幅越大. 经计算，Ptcr/Pccr的均值为0.566，说明将腹板简化为四边简支的均匀受压板将高估锈损试件的临界屈曲荷载，究其原因为锈蚀后腹板呈不均匀受压状态且翼缘对腹板的约束作用降低，弹性稳定系数kw宜适当减小.

3   极限荷载计算方法

《冷弯型钢结构技术规范》（征求意见稿）的有效宽度法考虑了畸变屈曲对部分加劲板件受压稳定系数的影响，弥补了现行规范[23]的不足. 由于有效宽度法计算过程繁琐，直接强度法（DSM）越来越受科研人员的青睐，其采用全截面特性计算冷弯薄壁型钢的极限荷载，并充分考虑了畸变屈曲的影响. 文献[23]第1.0.3条指出该标准未考虑受有侵蚀作用的冷弯型钢结构的特殊要求，因此，有效宽度法和直接强度法能否用于计算锈损C形钢轴压短柱的极限荷载还有待研究. 本文将考虑钢材力学性能退化和厚度折减对有效宽度法和直接强度法进行修正，使其适用于计算锈损C形钢轴压短柱的极限荷载.

3.1   有效宽度法

文献[23]中均匀受压板件的有效宽厚比按式（7）计算，其中计算系数ρ按式（8）计算，极限荷载按P cu = φfy Ae计算.

式中：b为板件宽度;t为板件厚度;be为板件有效宽度;k为板件受压稳定系数;k1为板组约束系数;σ1 = φfy，φ为轴心受压构件稳定系数，fy为屈服强度.

若将试件平均厚度ta与fy代入计算公式，得出的计算极限荷载Pcu1见表5，Pcu1与ηa的关系见图17. 文献[24]采用新修订的有效宽度法计算了202个未锈损的冷弯型钢轴压柱，得出试验结果与计算结果的均值为1.124，但本文的Ptu/Pcu1均值為0.990，标准差为0.034. 从图17可看出虽然Pcu1也随着ηa的增大呈线性下降，但其下降速率k2 = 537.12，比试验极限荷载的下降速率k1 = 660.95要小很多.

综上所述，采用有效宽度法计算锈损C形钢轴压短柱的极限荷载时，若按试件平均厚度进行计算将高估其承载力，因此需考虑厚度不均匀变化对极限荷载的影响.

文献[25]发现随着锈蚀率的增大，冷弯薄壁型钢的弹性模量Es逐渐降低，但新修订的有效宽度法未考虑弹性模量变化对有效宽厚比的影响，式（7）默认钢材的弹性模量为2.06 × 105 MPa. 文献[26]给出了有效宽度be的计算过程，be与Es的关系详见式（9），可看出be与■成正比. 为考虑弹性模量的降低对锈损试件极限荷载的影响，将式（10）代替式（7）计算有效宽厚比，其中E0 = 2.06 × 105 MPa，Es参照表1的实测结果. 此外，为考虑锈损短柱的截面损失和厚度不均匀变化，将式（10）中的厚度t均按式（11）计算.

修正后有效宽度法得出的计算极限荷载Pcur1见表5，P tu/Pcur1的均值为1.123，标准差为0.028. 图18给出了有效宽度法计算结果与试验结果的对比，可看出Pcur1的下降速率为kr1 = 694.19，与P tu的下降速率k1 = 660.95比较接近. 综上所述，修正后的有效宽度法能较好地预估锈损C形钢轴压短柱的极限荷载，并留有足够的安全储备.

3.2   直接强度法

《冷弯型钢结构技术规范》（征求意见稿）的附录给出了直接强度法计算轴压构件极限荷载的公式. 局部与整体相关屈曲承载力应按式（12）计算：

式中：σcr1为弹性局部屈曲临界应力;kw为腹板局部相关屈曲系数.

采用直接强度法计算锈损C形钢轴压短柱的极限荷载时，最重要的是计算Ncr1. 式（15）计算kw时考虑了板组效应，目前尚无锈蚀试件板组效应的相关研究，因此修正后的直接强度法未考虑板组效应. 另外，为考虑钢材力学性能下降的影响，屈服强度fy和弹性模量Es参照表1的实测结果;为考虑厚度不均匀变化对承载能力的降低，厚度t按式（11）计算.

图19给出了直接强度法计算结果与试验结果的对比，修正前后的计算结果见表6和表7，其中Pcu2为修正前的计算极限荷载，Pcur2为修正后的计算极限荷载. Ptu/Pcu2的均值为0.860，标准差为0.034;Ptu/Pcur2的均值为1.045，标准差为0.026. 因此，修正后的直

接强度法能较好地预估锈损C形钢轴压短柱的极限荷载（强度曲线如图20所示），其安全性提高，计算结果离散程度减小. 另从表6和表7可看出随着平均厚度损失率ηa的增大，试件的整体承载力Nne和局部屈曲临界荷载Ncrl逐渐下降. 修正后的Nne和Ncrl减小，λ1 = 增大，计算极限荷载Pcur2降低.

4   结   论

1）锈蚀导致冷弯薄壁C形钢的力学性能退化，屈服强度fy随着锈蚀率的增大呈线性下降趋势，应力-应变曲线主要表现为弹性阶段变短、屈服点下降和屈服平台变短甚至消失.

2）锈损C形钢轴压短柱的平均厚度损失率ηa小于10%时，试件的破坏模式为腹板局部屈曲. 试件锈蚀后腹板表面粗糙不平，局部屈曲多发生在腹板最薄弱处.

3）锈损C形钢轴压短柱的侧向位移和应变的增长速率随着锈蚀率的增大而逐渐增加，且锈蚀越严重，腹板宽厚比越大，局部屈曲变形越充分，屈曲后荷载与极限荷载的比值有增大趋势.

4）锈损C形钢轴压短柱的极限荷载、极限位移和极限应力均随着平均厚度损失率的增大逐渐下降，其中极限荷载呈线性下降趋势.

5）考虑钢材力学性能退化并利用厚度折减修正的有效宽度法和直接强度法均能较好地预估锈损C形钢轴压短柱的极限荷载，但修正后的直接强度法更接近试验结果，修正后的有效宽度法偏于保守.

参考文献

[1]    张中权. 冷弯薄壁型钢结构设计手册[M]. 北京：中国建筑工业出版社，1996：2—4.

ZHANG Z Q. Design manual for cold-formed thin-walled steel structures [M]. Beijing：China Building Industry Press，1996：2—4. （In Chinese）

[2]    李元齐，徐厚军. 我国冷弯型钢结构发展现状及展望[J]. 建筑结构，2019，49（19）：91—101.

LI Y Q，XU H J. Research and development of cold-formed steel structures in China[J]. Building Structure，2019，49（19）：91—101. （In Chinese）

[3]    彭雄，杨娜，王彬，等. 冷弯卷边槽钢轴压屈曲机理试验与数值研究[J]. 湖南大学学报（自然科学版），2013，40（8）：34—39.

PENG X，YANG N，WANG B，et al. Experimental research and simulation on lipped channel under axial compression[J]. Journal of Hunan University （Natural Sciences），2013，40（8）：34—39. （In Chinese）

[4]    史炜洲，童乐为，陈以一，等. 钢材腐蚀对住宅钢结构性能影响的评估[J]. 建筑结构，2013，43（16）：88—92.

SHI W Z，TONG L W，CHEN Y Y，et al. Assessment of influence of steel corrosion on behavior of residential steel structures[J].Building Structure，2013，43（16）：88—92. （In Chinese）

[5]    邱斌，徐善華. 锈蚀钢板力学性能的退化规律[J]. 机械工程材料，2014，38（10）：60—63.

QIU B，XU S H. Deterioration law of mechanical properties of corroded steel plates[J]. Materials for Mechanical Engineering，2014，38（10）：60—63. （In Chinese）

[6]    易伟建，雷国强.锈蚀钢筋混凝土偏心受压柱承载力试验研究[J]. 湖南大学学报（自然科学版），2008，35（3）：6—10.

YI W J，LEI G Q. Experimental research on the bearing capacity of corroded reinforced concrete columns[J]. Journal of Hunan University （Natural Sciences），2008，35（3）：6—10. （In Chinese）

[7]    聂彪，徐善华. 冷弯薄壁型钢腐蚀研究现状及展望[J]. 太原理工大学学报，2019，50（6）：743—748.

NIE B，XU S H. Research status and prospect of cold-formed steel corrossion[J]. Journal of Taiyuan University of Technology，2019，50（6）：743—748. （In Chinese）

[8]    张世骥，赵东拂，幸坤涛，等. 2 mm厚冷弯薄壁型钢腐蚀后材料力学性能研究[J]. 工业建筑，2016，46（4）：114—119.

ZHANG S J，ZHAO D F，XING K T，et al. Study on material mechanical performance of corroded cold-formed 2 millimetre thin-walled steel[J]. Industrial Construction，2016，46（4）：114—119. （In Chinese）

[9]    徐善华，李柔，苏超，等. 锈损冷弯薄壁型钢材料力学性能试验[J]. 哈尔滨工业大学学报，2018，50（12）：74—80.

XU S H，LI R，SU C，et al. Mechanical property tests on cold-formed thin-walled steel materials with rust loss[J]. Journal of Harbin Institute of Technology，2018，50（12）：74—80. （In Chinese）

[10]  XU S H，ZHANG Z X，LI R，et al. Effect of cleaned corrosion surface topography on mechanical properties of cold-formed thin-walled steel[J]. Construction and Building Materials，2019，222：1—14.

[11]  徐善华，王皓，薛南. 锈蚀钢材偏心受压钢柱承载性能退化规律[J]. 哈尔滨工业大学学报，2016，48（6）：157—163.

XU S H，WANG H，XUE N. Deterioration law of bearing properties for corroded eccentric steel columns[J]. Journal of Harbin Institute of Technology，2016，48（6）：157—163. （In Chinese）

[12]  KARAGAH H，SHI C，DAWOOD M，et al. Experimental investigation of short steel columns with localized corrosion[J]. Thin-Walled Structures，2015，87：191—199.

[13]  XU S H，ZHANG Z X，QIN G C. Study on the seismic performance of corroded H-shaped steel columns[J]. Engineering Structures，2019，191：39—61.

[14]  BEAULIEU L V，LEGERON F，LANGLOIS S. Compression strength of corroded steel angle members[J]. Journal of Constructional Steel Research，2010，66（11）：1366—1373.

[15]  史炜洲，童乐为，陈以一，等. 腐蚀对钢材和钢梁受力性能影响的试验研究[J]. 建筑结构学报，2012，33（7）：53—60.

SHI W Z，TONG L W，CHEN Y Y，et al. Experimental study on influence of corrosion on behavior of steel material and steel beams[J]. Journal of Building Structures，2012，33（7）：53—60.（In Chinese）

[16]  SHARIFI Y，RAHGOZAR R. Remaining moment capacity of corroded steel beams[J]. International Journal of Steel Structures，2010，10（2）：165—176.

[17]  NIE B，XU S H，WANG Y D. Time-dependent reliability analysis of corroded steel beam[J]. KSCE Journal of Civil Engineering，2020，24：255—265.

[18]  WANG H，XU S H，LI A B，et al. Experimental and numerical investigation on seismic performance of corroded welded steel connections[J]. Engineering Structures，2018，174：10—25.

[19]  CASCINI L，PORTIOLI F，LANDOLFO R. Probabilistic time variant assessment of thin-walled steel members under atmospheric corrosion attack[J]. Journal of Civil Engineering and Management，2014，20（3）：404—414.

[20]  金屬材料拉伸试验第1部分：室温试验方法：GB/T 228.1—2010[S]. 北京：中国标准出版社，2010：1—19.

Metallic materials-tensile testing-Part 1：Method of test at room temperature：GB/T 228.1—2010[S]. Beijing：Standards Press of China，2010：1—19. （In Chinese）

[21]  GALAMBOS T V. Guide to stability design criteria for metal structures[M]. 5th ed. New York：John Wiley and Sons，1998：78—143.

[22]  王春刚.单轴对称冷弯薄壁型钢受压试件稳定性能分析与试验研究[D]. 哈尔滨：哈尔滨工业大学，2007：26—32.

WANG C G. Stability behavior analysis and experimental study on singly-symmetric cold-formed thin-walled steel members under compression loading [D]. Harbin：Harbin Institute of Technology，2007：26—32. （In Chinese）

[23]  冷弯薄壁型钢结构技术规范：GB50018—2002[S]. 北京：中国计划出版社，2002：18—34.

Technical code of cold-formed thin-wall steel structures： GB50018—2002[S]. Beijing：China Planning Press，2002：18—34. （In Chinese）

[24]  王春刚，孔德礼，张耀春. 冷弯薄壁型钢构件承载力计算方法对比研究[J]. 建筑钢结构进展，2017，19（6）：51—59.

WANG C G，KONG D L，ZHANG Y C. Comparative study on calculation methods of bearing capacity of cold-formed thin-walled steel members[J]. Progress in Steel Building Structures，2017，19（6）：51—59. （In Chinese）

[25]  NIE B，XU S H，YU J，et al. Experimental investigation of mechanical properties of corroded cold-formed steels[J]. Journal of Constructional Steel Research，2019，162：1—12.

[26]  陈绍蕃.钢结构设计原理[M]. 4版. 北京：科学出版社，2016：384—398.

CHEN S F. Principles of steel structure design[M]. 4th ed. Beijing：Science Press，2016：384—398. （In Chinese）