矿石体重不同分析方法的对比探讨——以长山锌金多金属矿床为例

黄建，黄家龙，赵坦

(华东冶金地质勘查研究院，合肥 230088)

0 引言

在矿体储量计算的参数中，元素品位，块段的面积、体积以及矿体厚度等参数都可以比较准确地获得，但是体重这一参数却很难准确地获取。早期的勘查工作中的体重取值主要按样本可分的类型分别求取其平均值作为经验值参加储量的计算[1]。在20世纪80年代，有部分学者尝试建立数学模型进行分析，主要包括线性回归及理论计算[2-4]，但由于计算过于繁琐，应用受到一定的限制。随着计算技术的发展，应用基于最小二乘法的线性回归理论参与体重计算已经越来越普遍，是目前建模计算矿石体重的主流方法，且取得了较好的效果[1,5-10]。人工智能神经网络是一种发展较晚的算法模型，在20世纪90年代末期有人开始进行尝试用于矿石体重的分析[11-12]，进入21世纪以来相关理论研究和软件技术已经很成熟。

但是，在回归模型中尤其是多元线性回归模型，很多学者用体重数值直接参加回归计算，很少探讨用体重倒数参与回归进行优化；同时部分学者主张，对于多种硫化物矿石的矿床，因为多重共线性应该用扣减硫参与回归[6]。本文将针对这2点对多元线性回归模型进一步优化，并建立新的神经网络模型与之对比。

1 矿床地质特征

1.1 矿体地质特征

长山锌金多金属矿位于安徽省宣城市狸桥镇，矿体主要赋存于石炭系细晶灰岩和白云质灰岩的接触界面附近，沿层间构造滑脱面、构造裂隙充填产出，多呈似层状、透镜状，其主要赋存深度为1000～1400 m。矿体围岩为碳酸盐岩，岩性稳定，岩石组成成分简单。该矿床为多金属矿，主要工业矿种有铅、锌、金、银、硫及少量铜等，锌和金已到中型规模。

矿体矿石矿物为闪锌矿、方铅矿、磁黄铁矿、黄铁矿、黄铜矿、毒砂、自然金、自然银，以闪锌矿、方铅矿、黄铁矿为主，次为黄铜矿、磁黄铁矿、毒砂等。脉石矿物主要为方解石，少量白云石。

矿石结构主要为自形-他形晶结构、压碎状结构、显微固溶体分离结构、交代浸蚀结构。矿石构造主要为块状构造，其次有浸染状构造、纹层状构造。

1.2 矿石体重及成矿元素分析

本次选取41个样品进行小体重和主要成矿元素品位的分析测试，测试结果如表1所述。

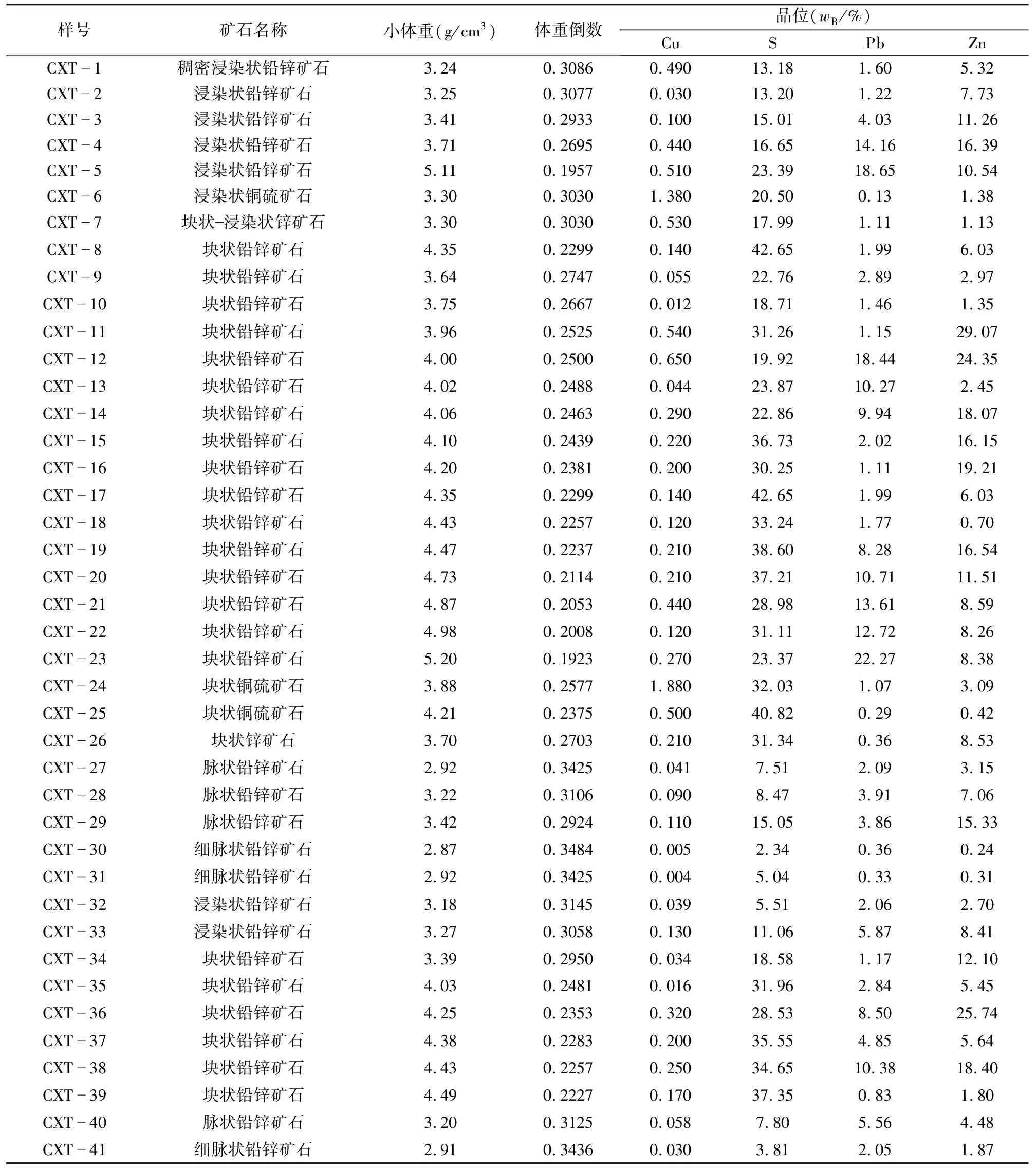
表1 主要成矿元素品位及小体重值Table 1 Content of the main ore element and the small volumetric weight values

测试结果显示，矿石体重范围为2.87～5.2 g/cm3，平均值3.88 g/cm3。本矿床矿石多为致密块状，湿度与空隙较小，不作校正。可以看出，矿石体重的变化范围大，应用传统方法计算矿床体重明显不适用，会给储量计算带来较大的误差。

测试结果显示，本矿床主要工业元素有Zn、Pb、Au、Ag、S、Cu等6种元素。在41个样品中，w(Cu)=0.004%～1.880%，平均值0.23%；w(Pb)=0.13%～22.27%，平均值5.31%；w(Zn)=0.24%～29.07%，平均值8.73%；w(S)=2.34%～42.65%，平均值23.45%；共生有较多的金和银矿，但因其品位相对很低，对矿石体重基本无影响，因而不予考虑参与体重预测。

主要成矿元素物相分析结果，如表2所述。

表2 主要成矿元素物相分析结果Table 2 Phase analysis of the main ore elemen

Cu元素。主要以黄铜矿的形式存在，多呈显微乳滴状分布在闪锌矿晶体中，为固溶体分离形成的产物。矿石中原生硫化铜占93.55%～97.37%(见表2)，次生硫化铜占2.46%～5.81%，矿石中以硫化铜为主，两者相加占94.57%以上，另外有少量的氧化铜。

Pb元素。主要以方铅矿形式存在，为粒状晶体，呈浸染状分布于矿石中，块状矿石中氧化矿物(铅钒、白铅矿、铅铁矾)的含量很高，占68.00%～74.86%，方铅矿占25.14%～32.00%(见表2)；脉状矿石(白云质灰岩中产出)中主要为方铅矿，占56.74%，氧化矿物中的铅占43.26%。由于矿体埋深较大，且矿石多较致密，因而原生矿中氧化铅的含量很少，岩矿鉴定中未见到明显的氧化铅矿物，因而推测氧化铅应为样品采出后至化验分析过程中氧化而来，主要的原生铅矿物相应为硫化矿。

Zn元素。主要以闪锌矿形式存在，为不规则粒状晶体，具固溶体分离结构，大部分晶体呈集合体赋存。矿石中的锌主要以其他形态锌矿物、硫化锌存在，占84.57%～95.28%(见表2)，以其他形态锌矿物中锌为主，其次是硫化锌中的锌，氧化物中锌占2.92%～5.96%。

S元素。主要以黄铁矿、闪锌矿、方铅矿形式存在。黄铁矿为不规则粒状或胶状晶体，晶体呈集合体赋存，有的晶体在闪锌矿中呈包裹体。矿石中的硫主要为硫化物，占69.56%～74.45%(见表2)；次为硫酸盐，占18.05%～20.71%；自然硫占7.43%～9.73%。

综上，各成矿元素均存在多种物相，赋存于多种矿物中，但主要还是赋存于硫化物中，考虑到本矿床埋深较大，矿石多为致密块状构造，因此氧化的元素物相应为采样后暴露空气中形成。

2 矿石体重与矿石品位的关系

冯适安[2]通过函数推导构建了铅锌矿矿石体重与元素品位的理论模型。通过进一步拓展，可以推广运用到其他多金属矿床。其模型如下：

当不考虑矿石原生的裂隙和湿度时，假设脉石矿物体重为固定常数D0，可以是单个脉石矿物，也可以是多个密度较为接近的脉石矿物。设d1、d2、…、di为各矿石矿物的比重，c1、c2、…、ci为各成矿元素在其所赋存的矿石矿物内的品位，假设这3个参数都为常数，设k1、k2…ki为常数。

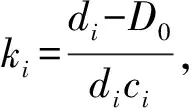
可以看出，在上述假设下，多金属矿床矿石的体重倒数与成矿元素品位之间存在线性关系，即：

上述模型是理想状态下得出的，比较简单。但是实际情况可能比较复杂，比如脉石由多种矿物组成，且其体重有较大差异，或者矿石矿物中成矿元素的品位存在一定变化，如闪锌矿中因为Fe2+和Zn2+可以以任意比例类质同象替代，其品位在同一矿床的闪锌矿中可能会存在较大变化。在这种情况下，可能需要更复杂的非线性数学模型来概括，甚至由于变量太多无法得出具有实用性的关系式，从这点来看，使用神经网络模型有一定优势。

另外，有学者[6]认为，当一种元素同时赋存于多种矿物中的时候，由于元素品位之间存在自相关性，比如方铅矿中的S和Pb元素，在已知Pb的品位时，可以估算出对应S的品位，因而认为诸如黄铜矿、闪锌矿、方铅矿等硫化物中金属元素和硫元素都参与小体重计算时，应该在全硫中将这部分的硫扣减掉(扣减后的剩余硫应该为正值)。但是这种做法是不正确的：首先因为有些硫化物(如闪锌矿)会有前述的类质同象，而且由本矿床物相分析结果可知，成矿元素并非全部以硫化物的形式存在，这样使得硫元素与成矿元素之间可能不具稳定的数学关系；其次，假设二者有确定的数学关系(如比较稳定的方铅矿)，也可以证明扣减硫和全硫参与线性回归时，其结果是一样的，证明如下：

设有一硫化物矿床，成矿元素有S和Pb，分别用全硫和扣减硫构建出y1和y2这2个体重的线性回归方程。其中w(Pb)、w(S)和w′(S)分别为铅、全硫和有效硫的品位，a、a0、a00、a1、a2、a11、a22均为常数，y1、y2代表体重，设铅和硫的相对原子质量分别为m和t。则有：

y1=a0+a1·w(Pb)+a2·w(S)

y2=a00+a11·w(Pb)+a22·w′(S)

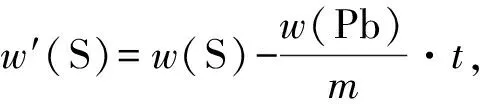
上述结论是假设方程的因变量为体重而得出来的，当因变量为体重倒数时，也可以得出相同的结论，因此多金属硫化物矿床的体重，其总硫无需扣减就可参与方程回归。该结论也将在下文的实例中得到证实。

3 多元回归预测模型

3.1 多元回归分析步骤

本次多元线性回归分析利用Excel加载的“数据分析”中的“回归”分析工具来进行，分析步骤如下：

(1)在Excel软件中，输入41个样本的体重值及Cu、Pb、Zn、S等4种元素的品位，同时计算体重倒数值。

(2)为验证前述矿石体重与品位的理论模型，本次分别以体重(y)和体重倒数(1/y)为因变量，4种元素为自变量，利用Excel软件设置好置信度(图1)，进行多元回归分析，得到模型和各变量的统计参数。

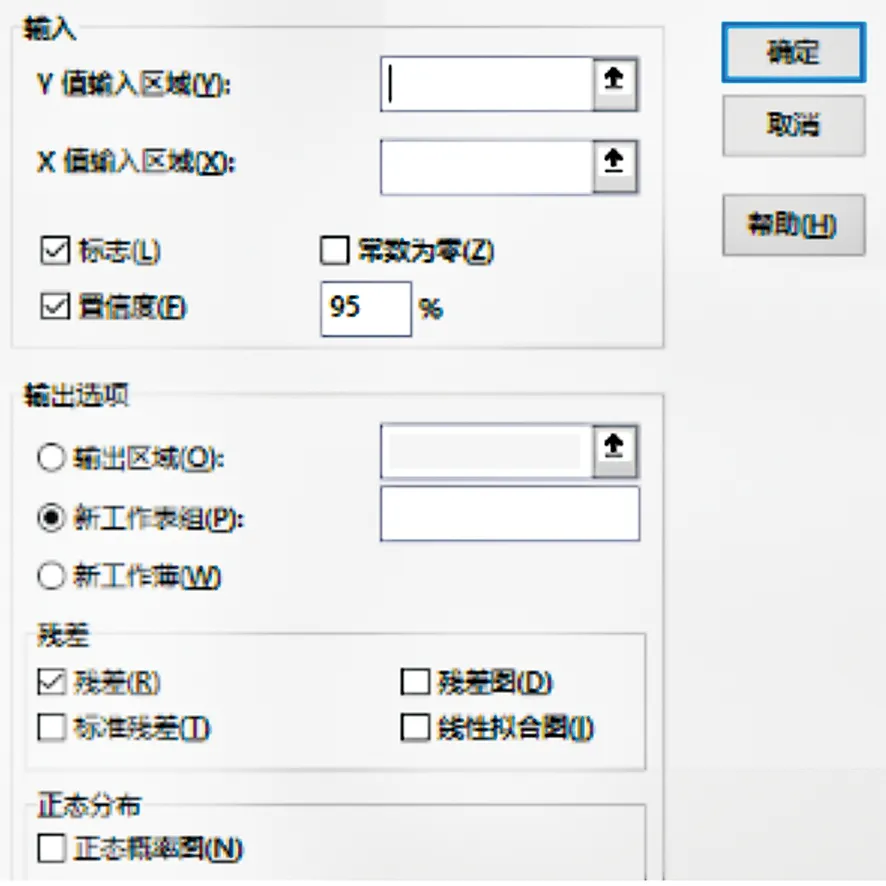
图1 Excel回归分析设置界面 Fig.1 Regression analysis interface set in Excel software

(3)对模型参数进行相关检验，包括R值、R2值、标准误差、回归系数、截距、F值以及t值等一系列参数。

(4)根据模型的检验结果，将不相关元素剔除，重新建立回归模型，并对新的模型再次进行检验，直到模型通过检验为止。

3.2 模型的建立和统计检验

数据导入后，将置信度设为95%，即取显著性水平α=0.05。分别将体重和体重倒数作为因变量进行回归分析，得到回归模型①、模型②(表3)和模型回归统计量(表4)。

在多元线性回归模型概述(表3)中，复相关系数R越大，表示小体重测定值与元素品位之间呈正线性相关越强；可决系数R2(RSquare)是测定多个变量间相关关系密切程度及其对因变量的联合影响程度的统计分析指标，其值越大则自变量对因变量的解释程度越高，模型的拟合越好；修正自由度判定系数(调整的)R2(AdjustedRSquare)用来衡量加入独立变量后模型的拟合程度，其值越大拟合程度越好；标准误差用来衡量拟合程度的大小。标准误差也用于计算与回归相关的其他统计量(表4)，此值越小，说明拟合程度越好[1]。根据以上判断标准，模型②略好于模型①。

此外，多元线性回归模型得出后，还需对其进行假设检验，主要包括2个方面，整体回归效应即回归方程的假设检验，一般用F检验，另外一个是偏回归系数即各自变量的假设检验，一般用t检验。回归模型①和②的F检验结果见表3，其自变量和截距的t检验结果见表4。

表3 多元线性回归模型概述Table 3 Summary of multiple linear regression model

可以看出方程①和②的F值分别为93.2737和126.4067，均远大于临界值2.633 5，说明模型方程的线性关系总体上是显著成立的。

回归模型通过F检验后，还要进行各自变量的t检验，表4中，根据各变量t统计值的绝对值大小和其临界值的比较结果，发现模型①的Cu以及模型②的Cu和Zn都接受了假设检验结果，而其余变量均拒绝了假设检验。说明这些元素在其相应模型中和因变量没有明显的相关关系，因此需要对模型进行进一步优化。

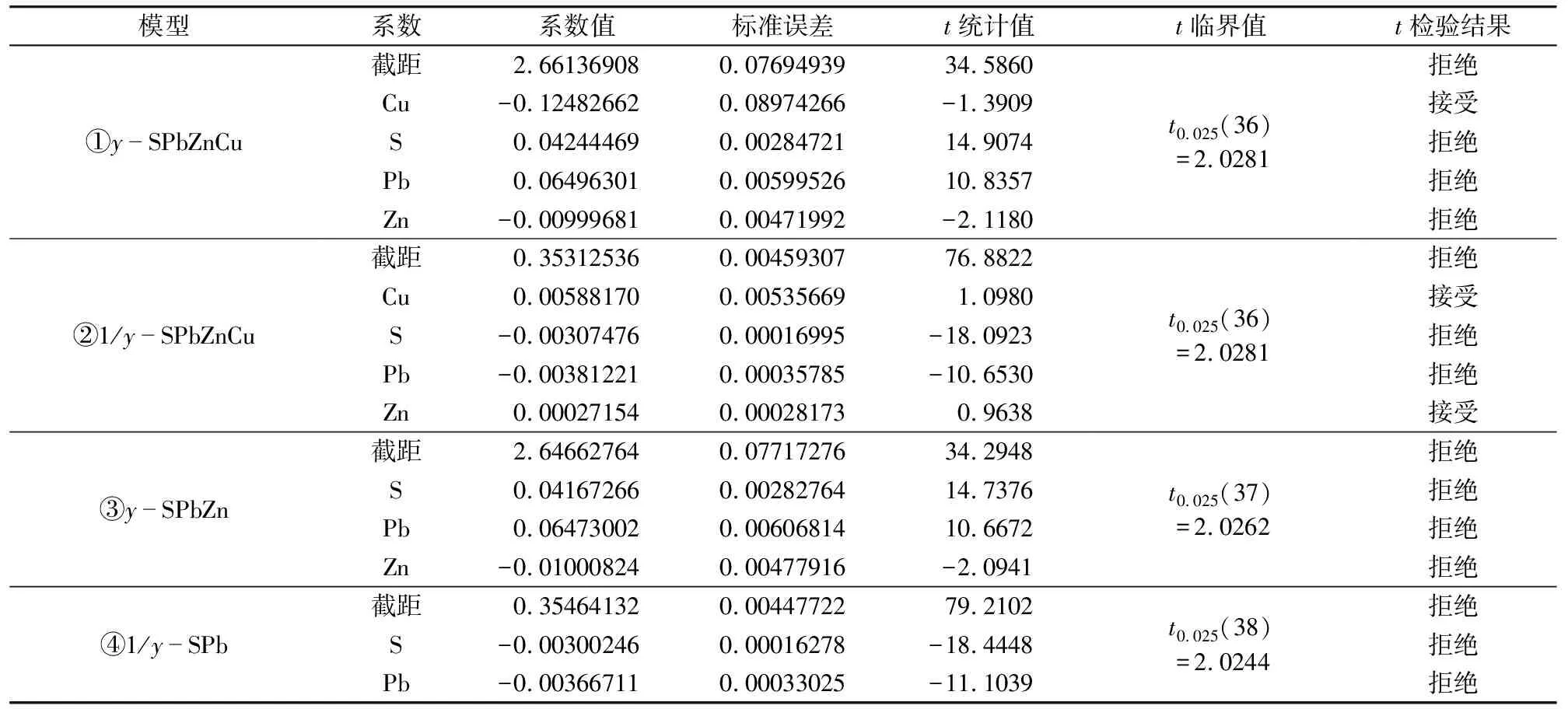
表4 多元线性回归统计量及其检验Table 4 Statistics and check of multiple linear regression

注：①y=a+a1·w(S)+a2·w(Pb)+a3·w(Zn)+a4·w(Cu)；②1/y=a-a1·w(S)-a2·w(Pb)-a3·w(Zn)-a4·w(Cu)；③y=a+a1·w(S)+a2·w(Pb)+a3·w(Zn)；④1/y=a-a1·w(S)-a2·w(Pb)。a、a1、a2、a3、a4分别为多元线性方程中变量的常数项。wB为元素的质量分数。

对模型①、模型②分别剔除Cu元素以及Cu、Zn元素后，重新优化分别得到回归模型③和模型④，其方程的显著性检验(F检验)和变量显著性的检验(t检验)结果见表3和表4。可以看出，这2个模型均通过了检验。因此，我们最终得到该矿床矿石体重和元素品位的2个拟合多元线性回归方程：

y=2.6466+0.0417·w(S)+0.0647·w(Pb)-0.0100·w(Zn)

模型③

1/y=0.3546-0.0030·w(S)-0.0037·w(Pb)

模型④

2个模型理论和实测的数据拟合情况，见图2。

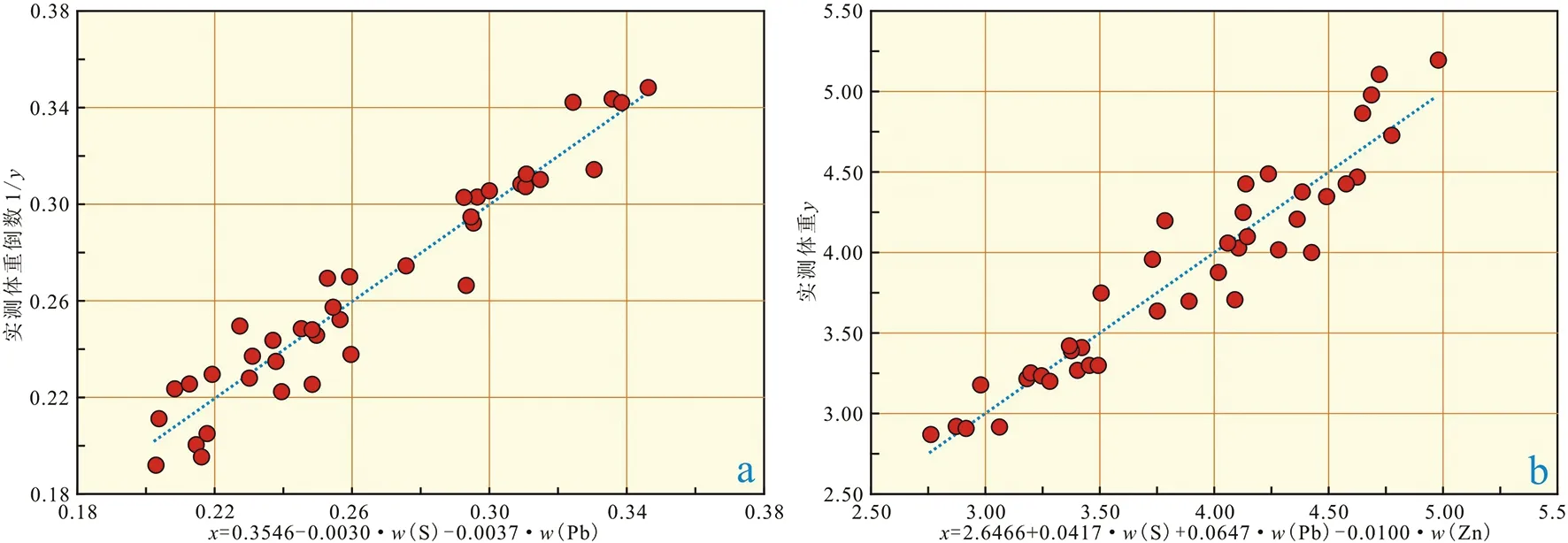
图2 回归模型拟合关系散点图Fig.2 Scattered point plot showing fitting relation of regression modela.体重倒数回归模型；b.体重回归模型

在图2中可见，2个模型都具有明显的线性趋势，而统计其误差数据发现，模型③的误差范围为0.05%～10.91%，均值3.96%；模型④的误差范围为0.05%～10.30%，均值3.63%，这说明模型④的整体效果要优于模型③，也验证了体重倒数和元素品位之间理论关系的可靠性。

4 神经网络预测模型

4.1 神经网络简介

人工神经网络(Artificial Neural Networks，简称ANN)是近年来兴起的对人脑进行信息接受和处理过程的数学模拟而得到的一种智能算法[13]。它由大量的、同时也是很简单的神经元广泛互连形成复杂的非线性系统，已经在信息处理模式识别、智能控制及系统建模等领域得到越来越广泛的应用[14]。与回归算法相比，该算法不需要建立已知的模型去验证，而是通过建立复杂的函数关系，只要变量之间存在相关关系即可。

目前应用最广泛、算法最成熟的人工神经网络算法是BP网络算法，该算法是一种采用最优化梯度快速下降法，经过网络训练后，预期样本输出与实际输出之间的均方误差最小。其主要结构包括输入层、隐含层(中间层)和输出层，向网络提供样本之后，人工神经元通过三层神经元的相互联系，在输出层获得网络的输入响应。之后，按照减小期望输出和实际输出之间均方查误差最小方向，逐层修正从输出层、隐含层之间的连接权重，最后再反馈到输入层[15]。

由于BP神经网络存在着收敛速度慢、稳定性不强等问题，有许多学者提出了改进算法，如共轭梯度法、牛顿法和Levenberg-Marquardt算法[16]。其中Levenberg-Marquardt全局优化算法，具有收敛速度快，拟合性能更强等优点，非常适用于网络训练，使得BP神经网络的每次迭代不是沿单一方向进行，同时通过自适应调整来优化权重，极大地提升了收敛速度，本文神经网络模型采用该种算法。

4.2 神经网络模型的建立

本次研究在MATLAB(R2016a)环境下神经网络拟合工具箱(Neural Net Fitting)中进行，该工具箱具有非常简洁实用的功能。具体操作分为3个步骤。

(1)将数据按照格式输入软件后，分别选择元素品位和体重为输入数据(Inputs)和目标数据(Targets)(图3a)。考虑到人工神经网络的特点，这里不将体重及其倒数分开，也不对元素进行优选，因为这些元素对体重理论上都是有贡献的，而用神经网络就是要通过训练建立这种隐含的(线性和非线性)关系。

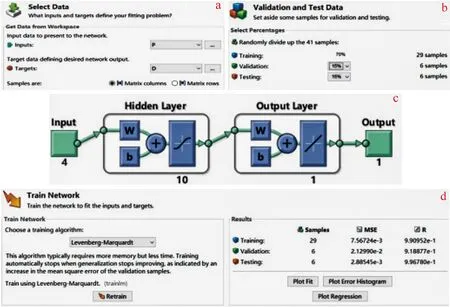
图3 神经网络拟合工具箱操作步骤Fig.3 Operation steps of neural network fitting toolbox

(2)选择网络训练(Training)、验证(Validation)、测试(Testing)3种类型数据的比例(图3b)。其中，训练数据是网络训练的主体，程序会据此生成一个模型，然后在验证数据中检验模型是否具有普适性，若没有普适性，会重新进行训练，如此往复循环，直到结果数据符合设定好的精度后停止训练；而测试数据不参与网络训练，但在网络训练结束时会参与整个模型的拟合精度计算，起到进一步验证的作用，这3类数据拟合效果都好时，整个模型才会有更好的可信度，减少偶然性。这3类数据采用70∶15∶15的近似比例，使程序按照这个比例对样本数据随机进行分配。

(3)设置隐含层的神经元个数，通过多次试验，确定隐含层神经元个数为10个。由此建立了网络结构，包括4个人工神经元的输入层(Input)、10个人工神经元的隐含层(Hidden layer)、1个人工神经元的输出层(Output layer)(图3c)；采用Levenberg-Marquardt改进算法对建立的网络进行训练(图3d左侧)。在图3d右侧界面，我们可以通过观察3种训练数据的均方差(MSE)和R值来判断训练结果的好坏，当数据不理想时，可以点击Retrain按钮再次训练，而系统会对数据再次随机进行分配。

通过多次训练后，模型目标输出与训练数据、验证数据、测试数据样本输出之间的相关系数分别是0.99095、0.91888和0.99678，与所有样本的相关系数为0.98895(图4)。

图4 神经网络模型各部分数据拟合关系图Fig.4 Diagram showing fitting relation of data of each part of the neural network model

训练结束后。统计神经网络训练结果和原始数据的误差，其变化范围为0.004%～7.742%，均值为1.826%。

5 模型对比探讨

5.1 最优模型的确定

对上述3个模型进行拟合精度的进一步对比，指标见表5。

可以看出体重回归模型、体重倒数回归模型和神经网络模型的R及R2值均依次增大，如前述这2个值越大说明拟合效果越显著，而神经网络模型的R及R2值明显高于回归模型。表5中平均绝对误差代表模型预测值与实际值绝对差值的平均值，平均相对误差为绝对误差占实际值百分比的平均值，均方根误差为预测值与实际值均方误差的平方根，这3个指标值越小表示模型精度越高。3个模型中这3个指标均越来越小，且神经网络模型指标明显小于回归模型。因此，综合来看，神经网络的各个指标值都明显优于多元回归模型，整体拟合精度高于多元回归模型，为最优模型；而在回归模型中，体重倒数回归模型拟合精度略优于体重回归模型。

表5 不同模型拟合精度对比Table 5 The fitting accuracy comparison for different models

另外，将41个样本按照体重倒数回归模型和神经网络模型预测值差值的绝对值从小到大排列为横轴，以不同模型相应体重为纵轴绘出的走势图(图5)可以看出，随着神经网络预测模型和回归模型结果偏差的增大，体重也有增大的趋势，当体重<4.0 g/cm3时，2种模型结果均与实际值相近，而当体重>4 g/cm3时，神经网络与实际值更接近，说明神经网络在体重较大时有更好的拟合效果。

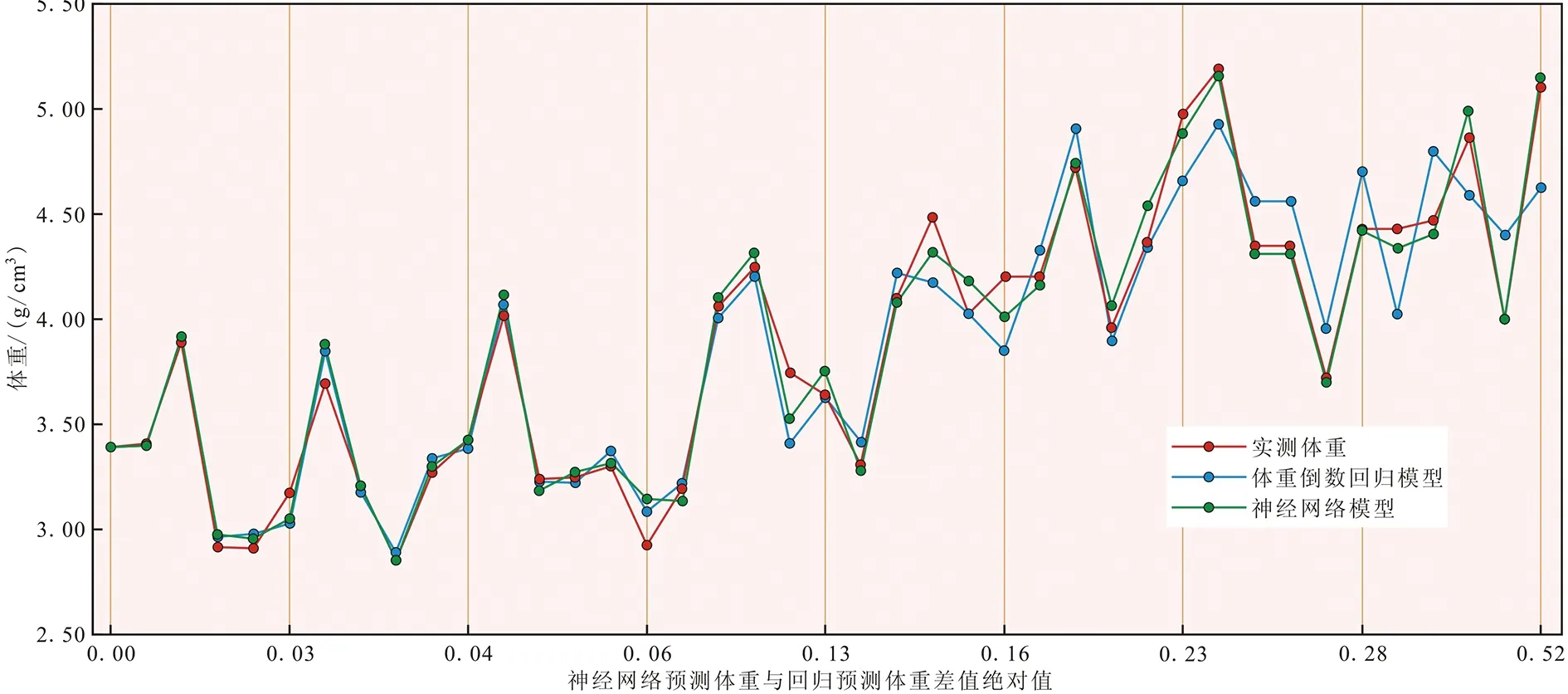
图5 不同模型预测结果与实际值比较图Fig.5 Comparison of actual results from different models

5.2 数据预测分析与应用

为了进一步验证体重倒数回归模型和神经网络模型，我们将地质勘查中所有的见矿单工程样品元素输入模型中，计算结果构成如图6所示。

图6横轴为按神经网络模型样品计算数据从小到大的排序，纵轴为预测体重。经对比可见，2种模型在整体趋势上比较接近，从而印证了模型的可靠性。按照前述结果，在数据可信度方面可以选择神经网络模型，进一步观察可以看出，在体重<3 g/cm3时神经网络输出数据略小于回归模型输出数据，而在3～4 g/cm3范围内神经网络输出数据略大于回归模型输出数据，>4 g/cm3后二者相互交错，规律比较紊乱，这一方面说明神经网络模型中体重与元素品位之间为非线性关系，同时也表明回归模型在一定体重范围(大致小于4 g/cm3)内与神经网络模型具有相似的精度，而在体重较大时，会出现较大的偏差。总体来说，神经网络模型在本矿床中有更广的概括度。

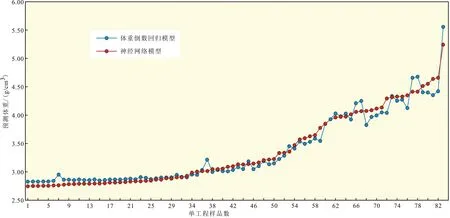
图6 单工程样品不同模型体重预测对比Fig.6 Volumetric prediction comparison of different models for single-engineered samples

因此，我们可以在计算储量时将划分的矿体块段各元素的平均品位输入神经网络模型中，通过训练好的程序快速计算出相应块段的体重，这样将使得矿床储量计算更加准确。

6 讨论

(1)本文中按照回归模型分析步骤，Zn和Cu元素均被剔除。究其原因，可能是因为Cu元素的含量较低，对体重的影响较小，而Zn元素在矿物内的含量不够稳定所致。虽然模型②(Cu和Zn元素未剔除)的R值略高，但这可能是一种过拟合的假象，显示多元线性方程无法表达出这2个元素与体重的隐含关系，因此神经网络在这方面表现出很强的优势。此外，想要提高回归模型精度，可能需要进一步研究闪锌矿的物质组分，由于闪锌矿中常含有一定量的Fe，因此补测Fe元素有可能会获得更好的结果。

(2)由于本次神经网络每次训练的样本分配都是随机选取的，因此仅训练一次可能无法达到理想结果，需要多次训练操作，也就是说，在有限时间内可能无法达到最优的效果，但是一般只要比回归模型有明显优势，就可以结束训练。

(3)从上述分析中可以看出，各种模型体重对矿石元素的依赖性都很强，选择有代表性的元素对获得较好的模型至关重要。因此在体重测试之前，应根据矿石全分析结果、矿物组成和主要成矿元素赋存状态等来确定对体重影响较大的元素。为节约成本，应主要选取可利用元素，因此无论是回归模型还是神经网络模型，对于脉石矿物简单的矿床最为适用，即脉石以一种矿物为主，或者密度接近的脉石矿物如方解石和石英，而矿石矿物分析一种稳定元素品位即可，但是矿物中的元素含量比例变化较大不稳定时，则需要考虑增加分析元素。此外还要考虑矿石是否致密且湿度稳定。

7 结语

(1)通过对模型的建立和优选，本次研究确定了2种多元回归模型，通过进一步精度对比优选，认为体重倒数与矿石元素之间存在更明显的线性相关，而利用MATLAB中神经网络工具箱建立的神经网络模型具有比回归模型更优的效果。

(2)在回归模型研究中，矿石中的锌元素含量比较高，但是没有通过模型检验被剔除，说明其对体重变化的解释能力较差，二者没有显著的线性相关关系，这可能与闪锌矿中Fe和Zn离子的相互替代有关，而神经网络模型因没有固定形式的数学模型受此影响较小。

(3)建立矿石体重和成矿元素之间的模型主要适用于脉石矿物种类少或主要脉石矿物的密度接近、矿石致密且湿度稳定的矿床(体)，同时成矿元素需要有较高的品位以保证能对体重产生影响。

(4)随着计算机技术的飞速发展，通过建立模型来分析矿石体重与元素品位之间的规律已越来越便捷，但是在便捷的同时应注意是否存在最优的模型，以更好地服务于矿山生产。本文中神经网络模型明显有更优的拟合精度同时操作界面简单，具有显著的应用价值。