基于BLUE与PCRLB的快速雷达资源管理*

罗 静，赵婵娟，方 明，汤继伟

(1.上海航天电子技术研究所，上海 201109;2.上海机电工程研究所，上海 201109)

0 引 言

相控阵雷达具有波束捷变能力，可以同时产生多个发射波束，分别独立地执行搜索、跟踪等任务[1]，波束驻留时间、波束的指向等参数值也可实时变化。在有限的雷达资源限制下，如何合理地对资源进行管理，使雷达作战能力最大化，具有重要的研究意义。

雷达资源管理主要分为目标跟踪和资源管理两个部分。资源管理部分利用目标跟踪反馈的目标信息对发射端资源进行实时分配。传统的资源管理方法主要有协方差控制[2]、基于信息熵值方法[3]。Alexey等人[4]将目标跟踪误差协方差作为评价函数，建立数学优化模型，对雷达的功率资源进行分配。该方法易受到滤波算法优劣性影响，因此Tharmarasa等人[5]提出将后验克拉美罗界作为目标跟踪精度衡量标准。严俊坤、秦童等人[6-7]将其作为评价函数，对雷达功率进行分配，后又提出一种波束和波束宽度的联合管理。后验克拉美罗界(Posterior Cramer-Rao Lower Bound,PCRLB)具有一定的预测性，通过计算上一时刻跟踪的贝叶斯信息矩阵(Bayesian Information Matrix,BIM)可以预测得到下一时刻的克拉美罗下界，为下一时刻雷达资源的分配提供了相关依据，可减少单次运算误差。

实际环境中，雷达跟踪问题大多是非线性量测下的跟踪滤波问题，多使用拓展卡尔曼滤波(Extended Kalman Filterr，EKF)算法、无迹卡尔曼滤波(Unscented Kalman Filter，UKF)算法、粒子滤波(Particle Filter，PF)算法和量测转换[8]等方法。EKF方法计算简单，但误差大；PF方法不受线性化误差或高斯噪声假定的限制，滤波精度高，但计算复杂度高，工程实际应用受限；UKF精度比EKF高，计算量较PF方法小；使用量测转换方法可以减少运算量，但传统转换测量过程中会产生误差，导致目标跟踪不一致性。针对这种情况，基于位置量测的无偏量测转换卡尔曼滤波算法[9]被提出，但该类型算法仍然存在误差的统计特性与实际不符等情况。之后最佳线性无偏估计器(Best Linear Unbiased Estimation,BLUE)被提出[10]，与UKF相比较，两者的跟踪精度近似，但BLUE算法计算量更小，更符合实时性的要求。综合计算量和跟踪性能，BLUE算法最佳[11]，可用于处理在极坐标系或者球坐标系下观测目标的跟踪问题，工作实时性好，跟踪精度高。

为进一步提高雷达资源管理实时性，本文提出了一种结合BLUE和PCRLB的快速资源管理算法。首先建立目标跟踪模型，使用BLUE算法进行目标跟踪，再快速计算PCRLB作为资源管理的依据，进行波束分配和驻留时间的优化。仿真结果表明，本文提出的算法在维持跟踪效果的同时可大幅降低运算量，更符合工程中实时性的要求。

1 基于克拉美罗下界的雷达资源管理

1.1 系统模型

假设雷达探测区域内有N个运动目标，雷达可以同时生成Q个波束照射目标。假设一个波束一次只能对一个目标进行照射，当Q>N即波束数目大于目标个数时，可使多余的波束执行搜索等其他任务；反之，当Q≤N时，需要对各个目标状态进行判断，选择被照射的目标以及确定波束的驻留时间。本文针对波束和驻留时间的联合管理展开研究。雷达通过资源管理模块对当前时刻目标信息进行处理，得到发射参数反馈给发射端，决定下一时刻的发射参数。

首先建立信号模型。假设雷达发射脉冲信号为s(t)，在k时刻有M个脉冲照射到目标，目标回波表达式为

exp(-j2πfd,k(m)t)+ωk(t,m)。

(1)

(2)

式中：ΔTk为波束驻留时间。式(2)说明目标回波信噪比与波束驻留时间、发射平均功率等参数有关。

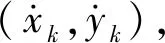
xk=Fxk-1+wk-1。

(3)

式中：wk-1～N(0,Q)为状态噪声，F为状态转移矩阵。

k时刻目标非线性观测方程为

(4)

目标观测向量为

(5)

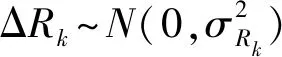
(6)

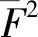
1.2 基于PCRLB的资源管理

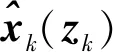
(7)

式中：E表示求取期望；J(xk)为目标状态xk的BIM，其逆即克拉美罗界CPCRLB(xk)，且满足

(8)

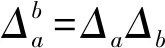
(9)

BIM计算涉及大量矩阵运算，为简便计算，Tichavsky[12]给出了一种迭代方法，将其表示为目标先验Fisher信息矩阵Jp(xk)和数据Fisher信息矩阵JD(xk)两部分之和，即

J(xk)=Jp(xk)+JD(xk)=

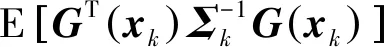
(10)

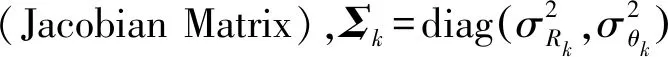
式(10)表明，J(xk)和JD(xk)均为驻留时间的函数，则对应的PCRLB也为驻留时间的函数。由于对角线上的元素分别为对应目标状态估计协方差提供一个下界，提取出目标跟踪精度误差方差的下界Cn：

Cn=CPCRLB(1,1)+CPCRLB(4,4) 。

(11)

式中：CPCRLB(1,1)和CPCRLB(4,4)分别为CPCRLB(xk)对角线上第一个和第四个元素。Cn为目标n的跟踪距离均方误差(Mean Square Error,MSE)提供了一个下界。

针对波束和驻留时间的联合管理展开研究，建立数学模型如下：

(12)

2 快速资源管理算法

结合式(10)～(12)发现，由于雷达观测是非线性的，使用传统跟踪算法诸如EKF或者UKF等方法对目标进行跟踪时，在每一时刻的资源管理求解中都涉及大量的雅可比矩阵的计算和求逆，导致运算量增加。针对此问题，本文提出一种结合BLUE和PCRLB的快速资源管理算法。

BLUE算法可用于解决非线性量测下的跟踪滤波问题，跟踪性能与UKF相当，但计算实时性更优。通过BLUE的卡尔曼滤波形式进行目标跟踪，在维持跟踪效果的前提下，提高了目标跟踪的实时性，同时避免雅可比矩阵计算，可快速计算PCRLB，为下文资源管理提供依据。

BLUE算法基本步骤如下：

(13)

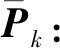
(14)

式中：Pk-1是k-1时刻的估计协方差矩阵。

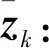
(15)

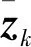
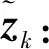
(16)

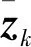
Step5 计算k时刻滤波增益因子Kk：

(17)

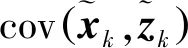
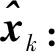
(18)

Step7 计算估计误差协方差矩阵Pk：

(19)

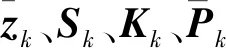
(20)

由上述假设经过推导[12]可得

(21)

式中：

(22)

计算S中对角线元素可得到

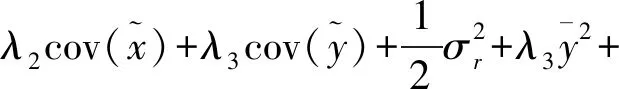
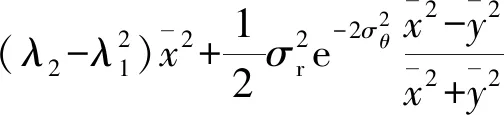
(23)

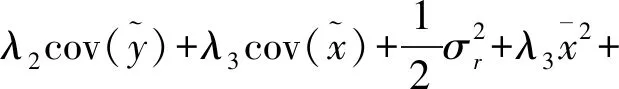
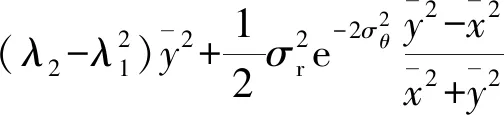
(24)

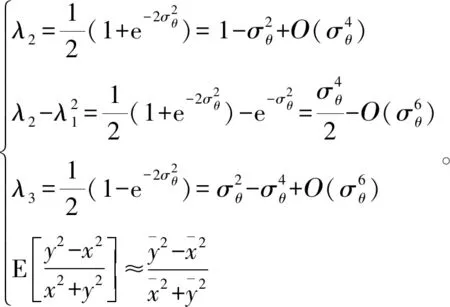
通过以上推导，计算转换后的量测误差的协方差矩阵为

(25)

将式(25)代入式(9)可得

(26)

相应地，可以得到信息矩阵JBLUE(xk)和克拉美罗界CBLUE：

JBLUE(xk)=Jp_blue(xk)+JD_blue(xk)=

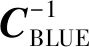
(27)

(28)

本文研究的波束和驻留时间的联合管理主要解决两个问题：一是如何选择下一时刻的跟踪对象；二是如何确定波束驻留时间。式(12)表示的模型直接求解难度大，对此，本文使用一种分步算法，分步解决上述两个问题。针对问题一，由式(10)可知，目标的先验信息矩阵与当前时刻的观测无关，仅反映过去时刻的目标跟踪效果，可求其逆用于选择下一时刻的跟踪对象。针对问题二，确定照射目标后，以目标PCRLB作为代价函数，驻留时间最短为目标函数，进行驻留时间的优化。

结合以上理论推导与分析，本文提出快速资源算法，具体步骤如下：

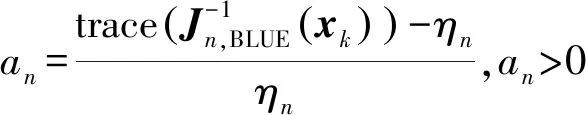
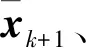
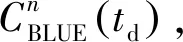
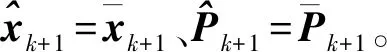
Step5 重复Step 1～4，完成跟踪。

同时，依据上述分析可知算法的计算量与lp3成正比，其中p为目标状态维数，l为可选驻留时间数目。

3 实验仿真与分析

采用仿真数据来验证本文算法的有效性。考虑到计算复杂性和结果直观性，设置2个波束对3个目标进行仿真，跟踪时间为60 s，驻留时间限制为0.01 s≤ΔTn,k≤0.45 s。脉冲重复周期Tpri=400 μs，脉冲宽度τ=10 μs，采样间隔为1 s。

设置目标初始协方差矩阵均为P0=diag[400,10,0.001,400,10,0.001]，初始信息矩阵均为J0=diag[0.5,1,0.001,0.5,10,0.001]，进行200次蒙特卡洛实验。将目标的均方根误差定义为

(28)

式中：Nmo为蒙特卡洛试验次数。

3.1 实验1：匀速直线运动

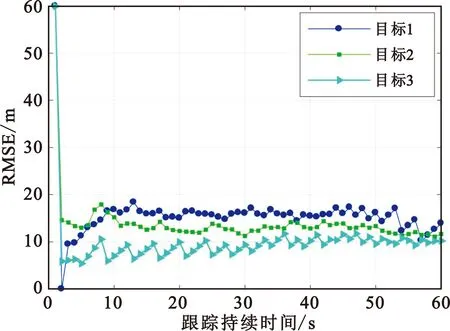
仿真场景如图1(a)所示，设置跟踪精度分别为300 m2、200 m2和150 m2。雷达位置即原点，三个目标均做匀速直线运动，目标1、目标2逐渐靠近雷达，目标3距离雷达较近，逐渐远离雷达。图1(b)为三个目标的跟踪误差均方根曲线图。

(a)三目标运动轨迹仿真图

(b) 目标跟踪RMSE曲线图图1 实验1仿真场景

图2为目标均方误差和PCRLB对比图。跟踪稳定后，目标MSE逐渐趋近PCRLB，由于算法以PCRLB作为比较准则，故MSE略高是合理的。以目标2为例，在0～10 s内，跟踪均方误差MSE产生小高峰，主要是由于初始条件相同情况下，算法倾向于将资源分配给跟踪效果最差的目标，导致其在跟踪初期未被跟踪或者分配驻留时间少。在第25 s时，MSE和PCRLB产生小尖峰，这是由于当前时刻目标未被波束照射，算法在此处以预测值代替滤波值。目标3初始距离雷达近，所需要的照射次数最少，导致曲线多起伏，目标逐渐远离时，为维持跟踪精度，照射次数增多，曲线起伏逐渐变小。

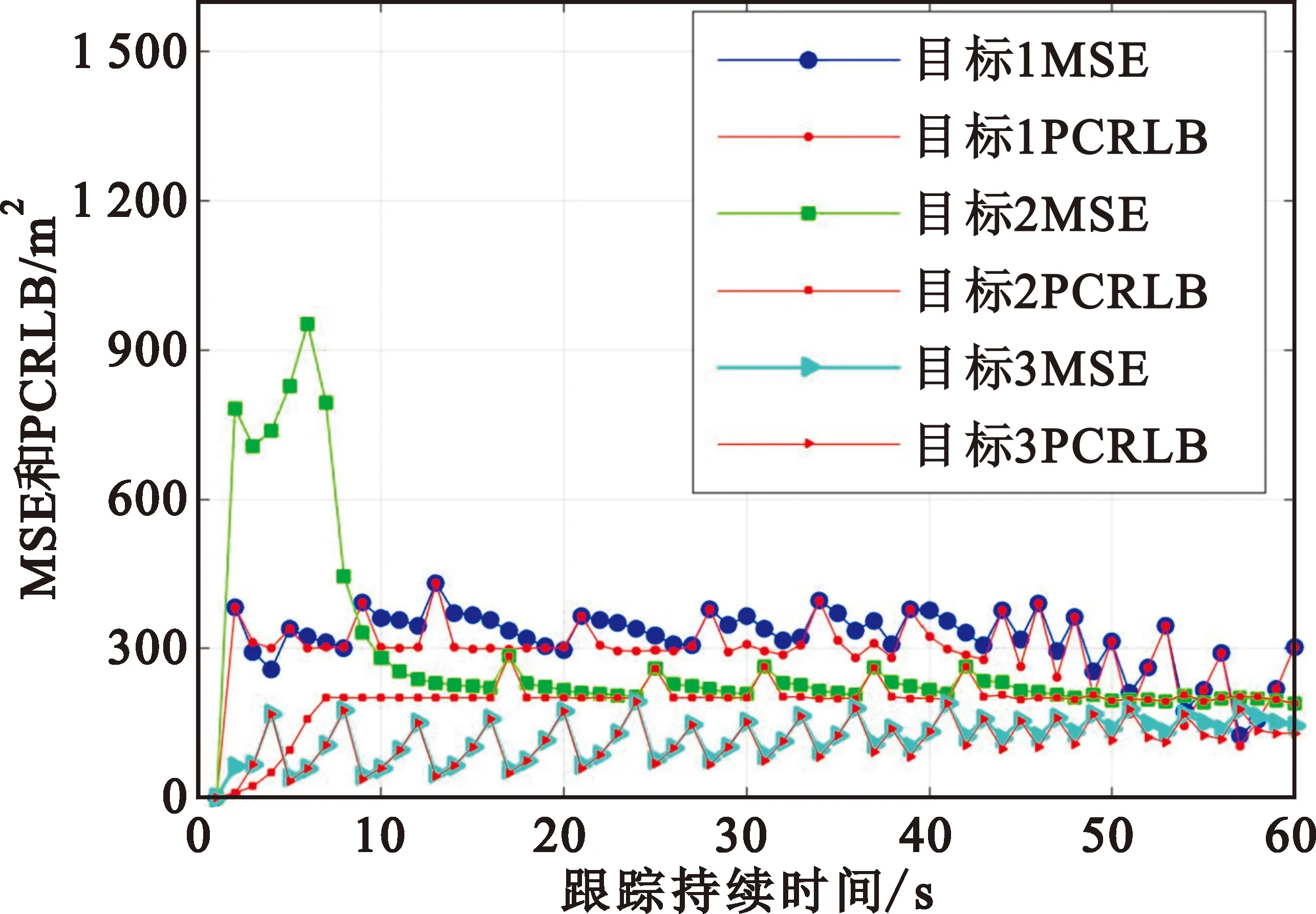
图2 实验1中目标MSE和PCRLB对比图

图3为算法优化后的驻留时间分布图，同一时刻雷达最多可对两个目标进行跟踪，驻留时间随目标靠近雷达而减少。同时，目标1和2与雷达距离近似，目标2期望精度高，所以所需的驻留时间高于目标1。目标2虽然距离雷达比目标1近，但是由于其期望精度高，所需要的驻留时间长。目标3逐渐远离雷达，所以波束照射次数逐渐增多，但由于距离雷达较近，驻留时间较少。与固定驻留时间相比较，本文提出算法可以在维持目标跟踪精度的同时，有效地对驻留时间进行实时管理，避免资源浪费。

图3 实验1中驻留时间分布图

选用基于UKF和PCRLB的传统资源管理算法作为对照组，使用相同的仿真初始条件和管理策略和方式，表1给出了本文快速算法和传统算法结果对比。可以看出，在具备i7平台的雷达资源调度模拟器上计算仿真，本文算法经过200次蒙特卡洛试验平均后，完成跟踪每一步的所需时间为1.8 ms，而传统方法每步跟踪所需的时间为20.9 ms，快速算法计算性能提高近11倍。

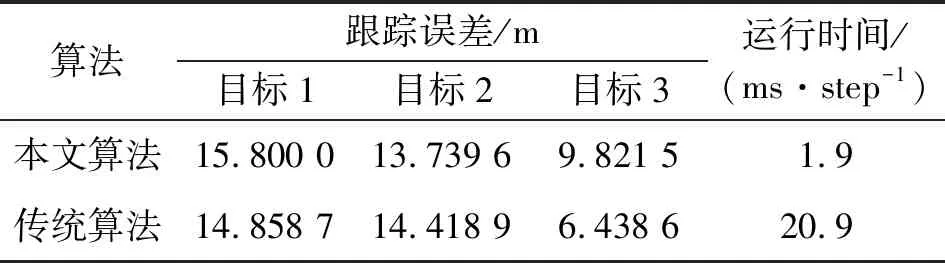
表1 本文算法和传统资源管理算法结果对比(匀速)

3.2 实验2：匀加速直线运动

仿真场景如图4(a)所示，目标加速度分别为沿x轴负向1g、y轴负向1g、x轴正向0.5g。图4(b)为三个目标跟踪RMSE曲线图。

(a) 目标运动轨迹仿真图(匀加速)

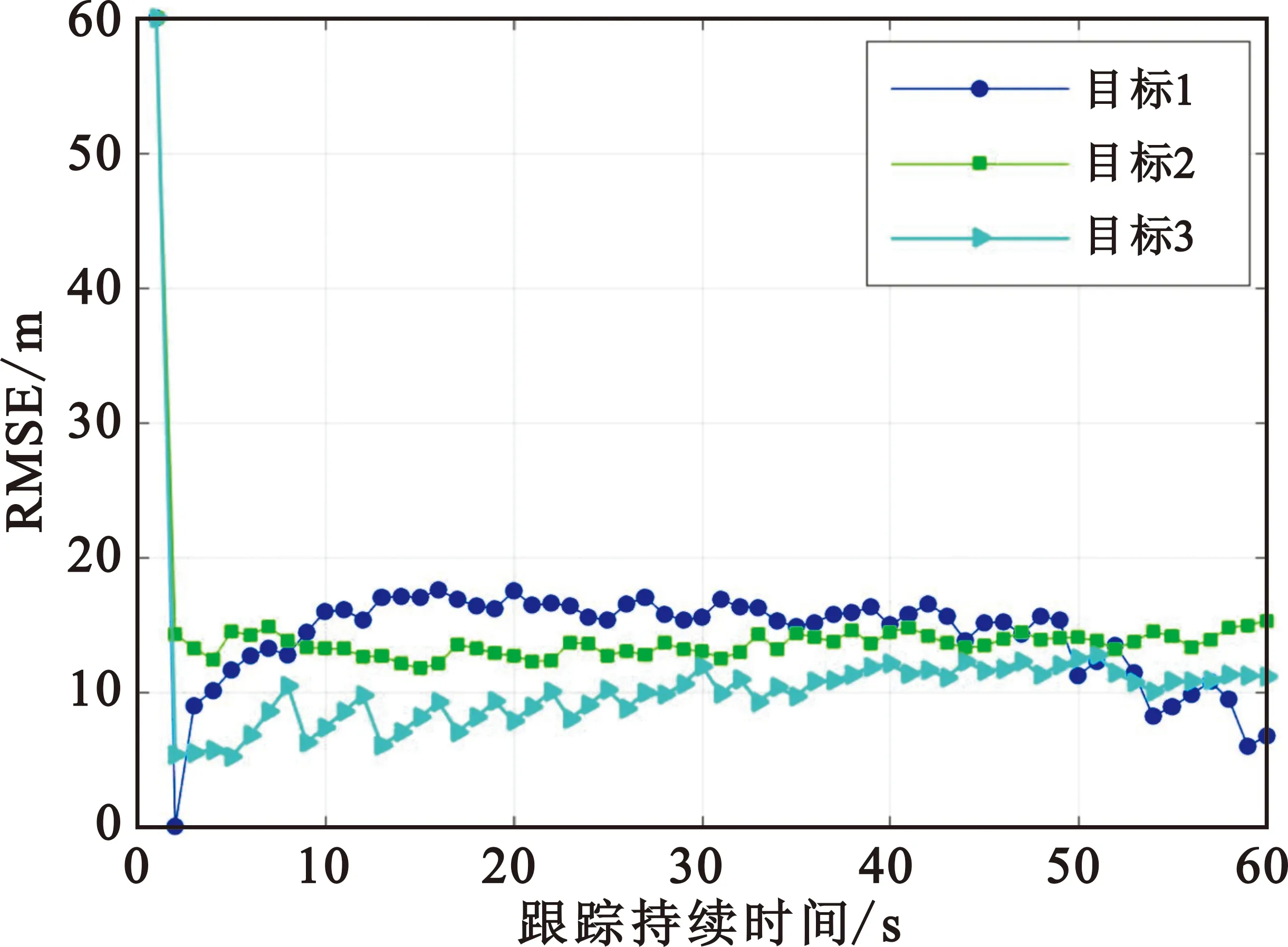
(b) 目标运动轨迹仿真图图4 实验2仿真场景

图5为目标MSE和PCRLB对比图。与匀速情况类似，由于波束数目小于跟踪目标数，在每一时刻的跟踪，都会优先选择跟踪效果较差的两个目标，导致曲线出现起伏。

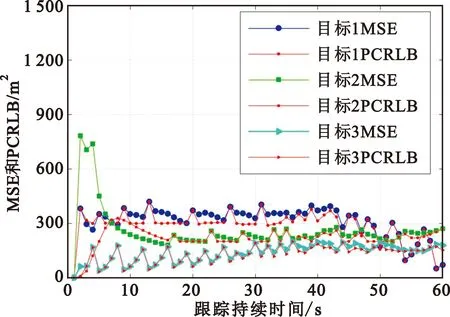
图5 实验2中目标MSE和PCRLB对比图

图6为匀加速目标的驻留时间分布图，图中黑色虚线为固定驻留时间0.2 s。目标2先靠近再远离雷达，对应的驻留时间的分布呈U型。目标1远离雷达，被波束照射的次数和照射的时间均减少，目标3则反之。结合以上分析可以看出，本文算法可以按照目标跟踪的需求，合理地分配驻留时间。

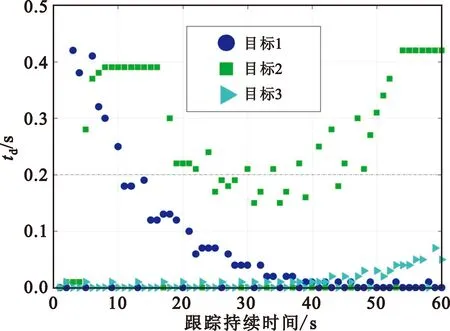
图6 实验2中驻留时间分布图

通过表2可看出，在具备i7平台的雷达资源调度模拟器上计算仿真，两种算法完成每一步跟踪的时间分别为1.8 ms和22.86 ms，本文所提算法对于匀加速运动的目标依然适用。综合算法分析，本文算法较传统算法运算速度高的原因主要有两点：一是BLUE作为跟踪算法实时性较UKF好，UKF滤波时，使用UT采样方法得到目标状态值、观测值预测，是一种以运算量获取高精度的方法；二是在计算PCRLB过程中，本文提出的快速算法避免了雅可比矩阵的重复计算，大幅减少了运算量，提高了运算的实时性。以上结果及分析说明算法有效可行。

表2 本文算法和传统资源管理结果对比(匀加速)

4 结束语

为提高雷达多目标跟踪任务情况下资源管理的实时性，本文提出了基于BLUE和PCRLB算法的雷达资源快速分配算法。使用BLUE算法对目标进行跟踪时，可得出更精确的转换后量测误差统计特性；同时，PCRLB为离散非线性滤波问题的均方误差提供了一个下界，可作为资源分配的代价函数。本文提出的快速资源管理算法通过BLUE算法跟踪目标，快速计算PCRLB，避免了传统过程中对雅可比矩阵的求解。以此为基础，建立了多目标雷达跟踪模型，并根据雷达跟踪效果和期望精度自适应地调整雷达的波束和驻留时间分配，实现了多目标雷达跟踪的资源自适应管理。最后结合试验仿真验证了该方法的可行性与高效性。

下一步将针对机动目标的实时跟踪问题，设计基于BLUE的交互多模型算法(IMM-BLUE)。