基于HOURGLASS网络语义关键点提取的光学图像空间目标姿态估计方法
李孟锡 任笑圆 王粲雨 逄 博,2 蒋李兵 王 壮
(1. 国防科技大学自动目标识别重点实验室, 湖南长沙 410073; 2. 杭州电子科技大学通信工程学院, 浙江杭州 310018)
1 引言
随着人类航天活动持续活跃,以卫星为代表的航天器在数目不断增加的同时,其所处的空间环境也变得日趋复杂。空间目标的三维姿态是反映其运动状态的重要参数,掌握准确的空间目标在轨姿态对于判断航天器工作状态、开展空间在轨操作、保障空间活动和太空资产安全具有重要的意义[1- 4]。近年来,以地基大口径望远镜、天基光学载荷等为代表的光学探测设备能力的不断提升,基于光学探测设备的空间目标三维姿态估计问题越来越受到研究人员的重视[5]。
目前,基于光学图像的空间目标姿态估计解决途径主要可归为两大类:(1)建立图像和姿态映射关系的方法[6-9];(2)根据特征关联解算姿态的方法[10-15]。第一类建立图像和姿态映射关系的方法通过构建目标在不同姿态下的图像模板库,然后将观测图像与模板库进行匹配,最终确定观测图像中目标的姿态[6-7]。随着深度学习被广泛应用在各个领域,李想[8]和徐云飞等人[9]开展了将深度学习应用于空间目标姿态估计的初步尝试,其基本做法是把姿态空间划分成不同的子空间,从而将姿态估计问题转换为分类问题或回归问题。然而,此类方法大多仅从二维观测图像出发,其估计精度取决于姿态空间的划分粒度。显然,随着估计精度要求的提升,这类方法需要更多的观测数据以实现姿态的精细化映射。考虑到空间目标的实测数据十分有限,此类方法在估计精度上存在天然的数据瓶颈。
不同于第一类建立图像和姿态映射关系的方法仅从二维观测图像出发的处理思路,第二类基于特征关联的方法是在已知目标三维模型的前提下,建立二维观测图像和三维模型之间的特征关联,然后根据特征关联结果解算目标的三维姿态。相比于第一类方法,这类基于特征关联的方法可解释性强且运算效率高。然而,目前主流的基于特征关联的方法大多都分解为特征提取和匹配关联两个阶段进行序贯处理[12],其在面对空间目标光学图像时,复杂多变的太空环境往往会导致观测图像出现降质从而显著降低图像特征提取的可靠性,影响后续特征关联匹配的正确率,并最终影响姿态估计结果的准确性。
针对上述空间目标光学图像姿态估计中存在的问题,本文提出了一种基于语义关键点提取的光学图像空间目标姿态估计方法,利用Hourglass网络端到端地提取包含语义信息的关键点,直接实现了光学图像中二维特征点与目标三维实体结构的关联映射,并在此基础上利用EPnP算法求解待估计的目标姿态值。仿真实验结果表明,其相比于现有方法能更好地兼顾算法估计精度和效率。
2 基于Hourglass网络语义关键点的空间目标姿态估计
如前所述,空间目标姿态估计的核心问题是建立二维光学图像特征点与目标三维实体结构的准确关联,其本质上是一个语义关键点提取的问题,即所提取的图像关键点中包含了与目标实体结构的映射关系。为此,本文引入深度学习领域中具备语义提取能力的Hourglass网络,其通过特定关键点对应特定通道的方法能够同时提取出关键点及其语义关联信息,可以为本文所研究的空间目标光学图像特征提取与特征关联问题提供端到端的一步解决途径。
本文所提方法的基本流程如图1所示,首先将空间目标光学图像输入至训练好的Hourglass网络,得到语义关键点,直接构建出光学图像中二维特征点与目标三维实体结构的关联映射,此时可把姿态估计问题转换为一个PnP问题。PnP为Perspective-n-Point的简称,是指已知三维空间和二维图像的n对特征点对之间的匹配关系,根据投影关系解算相机相对于目标的位姿的问题。基于Hourglass网络语义关键点提取的空间目标姿态估计方法流程图如图1所示。

图1 基于Hourglass网络语义关键点提取的空间 目标姿态估计方法流程图Fig.1 Flow chart of pose estimation method based on semantic key-point extraction via Hourglass network
2.1 基于Hourglass网络的语义关键点提取
Hourglass网络是一种可挖掘多尺度信息的网络,因其结构形如沙漏又被称为“沙漏网络”,常被用于人脸或人体关键点提取任务[16]。
Hourglass网络的基本组成为Residual模块,该模块的主要特点是在普通网络层中加入跳跃连接,其结构为由三个卷积层串联组成的普通网络层,中间交替插入ReLU,其结构如图2所示。

图2 Residual模块示意图Fig.2 Schematic diagram of Residual module
由Residual模块可构建Hourglass模块,二阶的Hourglass模块结构如图3所示,其内部包含两次下采样和两次上采样的过程,这种结构的设计可让网络提取到不同尺度下的特征信息。

图3 Hourglass模块示意图Fig.3 Schematic diagram of Hourglass module
针对本文所研究的问题背景,图4给出了本文采用的完整网络结构,它由两个二阶Hourglass模块堆叠形成,网络的输入是光学图像,其尺寸为H×W×3。因为在网络里有两次降采样的过程,所以输出关键点响应图的尺寸为输入图像尺寸的四分之一,为了让提取到的关键点具有语义性,每个通道响应图都只对应着特定的单一关键点,所以网络最终输出的关键点响应图尺寸为(H/4)×(W/4)×n,n为目标关键点数量。

图4 基于Hourglass模块的语义关键点提取网络结构图Fig.4 Key point extraction network structure diagram based on Hourglass module
结合空间目标光学图像的特点,在网络训练过程中,我们设计了基于l2范数的损失函数Loss(×),其表达式如下式所示,
(1)
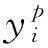
2.2 基于EPnP算法的空间目标姿态解算
由2.1节Hourglass网络提取出语义关键点后,便可获得三维空间和二维图像之间的匹配点对。此时,目标的姿态求解问题转换为PnP问题,本文利用EPnP算法[17]求解。
EPnP算法是目前解决PnP问题的常用方法,与其他求解方法相比其运算效率更高。EPnP的核心思想是在世界坐标系下选取四个不共面的控制点,然后根据投影模型解算出其在相机坐标系下的坐标,然后根据世界坐标系和相机坐标系下的对应点可解算出旋转矩阵R与平移向量t。具体来说,在如图5所示的坐标系定义下:
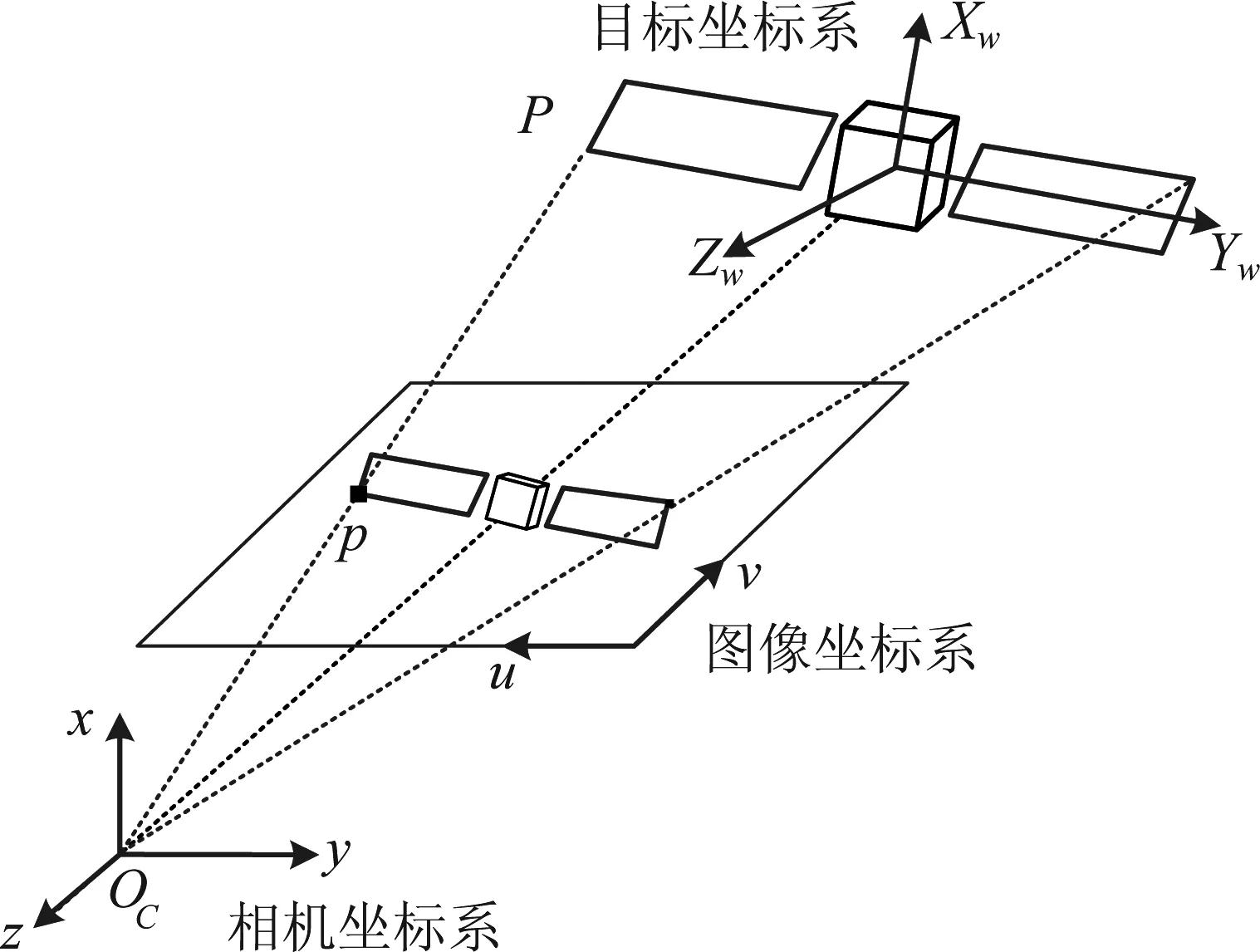
图5 摄像机坐标系和目标坐标系示意图Fig.5 Camera coordinate system and target coordinate system
设空间中某一点P在目标坐标系与摄像机坐标系下的齐次坐标分别是Xw=(Xw,Yw,Zw,1)T与x=(x,y,z,1)T,则存在以下关系:
(2)
将式(2)与经典的针孔成像模型联立可得到式(3):
(3)
其中,K为内参数矩阵,其只与摄像机的内部参数有关;H由摄像机相对于目标坐标系的方位决定,称为摄像机外部参数。所以对空间目标进行姿态估计的过程,就是已知摄像机的内参数矩阵求解出H中的R和t的过程。本文采用三维姿态角(俯仰角φ、偏航角θ和翻滚角γ)表示目标的三维姿态,目标三维姿态角定义如图6所示。
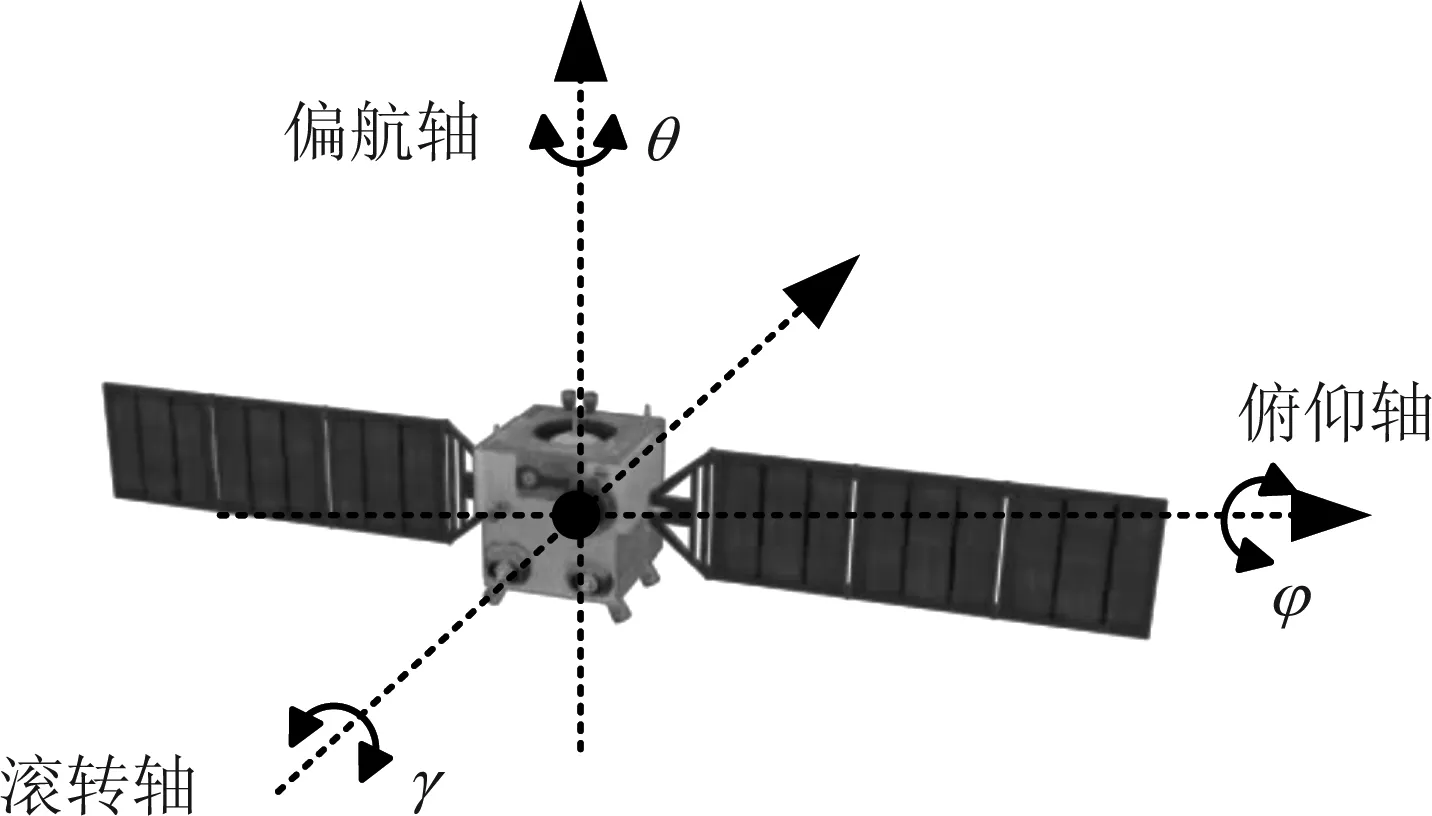
图6 三维姿态角定义示意图Fig.6 Schematic diagram of three-dimensional attitude angle
旋转矩阵R与三个姿态角(俯仰角φ、偏航角θ和翻滚角γ)之间存在如式(4)所示的转换关系:

(4)
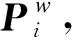
(5)
(6)
获得重心后,分别定义矩阵A和B
(7)
(8)
根据3D-3D相机位姿估计理论可知通过对H=BTA进行SVD分解便可求解姿态:
H=BTA=UΣVT
(9)
则旋转矩阵为:
R=UVT
(10)
平移量为:
(11)
3 实验结果与分析
3.1 实验数据集说明
因为实测图像数据难以获得且对应的空间目标真实姿态无法准确获知,所以本文利用仿真图像构造实验数据集来对本文姿态估计方法的性能进行验证。
实验数据集通过开源软件Blender对目标三维模型进行渲染仿真得到。在数据集构造过程中,我们对目标在{φ∈(-180°,180°],γ∈(-180°,180°],θ∈(-180°,180°]}的姿态角区间内每隔10°进行采样渲染,总共形成了46656幅仿真图像。在得到仿真图像后,还需要进一步标注出训练样本图像的关键点坐标以支持网络的训练。以“嫦娥一号”为例,我们选取出能反映目标结构特性和部件位置的12个关键点,其标注结果如图7所示。在具体的网络训练过程中,按照惯常做法,我们从实验数据集中随机挑选出其中的70%作为训练集,剩下的30%作为测试集。

图7 关键点标注示意图Fig.7 Schematic diagram of key-point marking
3.2 实验环境
实验测试的硬件平台主要参数为:Ubuntu 16操作系统,CPU为Intel(R)Core(TM)i-7800X,GPU为单块NVIDIA GeForce GTX1080 Ti显卡。深度网络实现框架为Pytorch1.1.0。
3.3 姿态估计结果与分析
利用本文方法进行空间目标姿态估计的过程如图8所示。输入图像首先通过Hourglass网络得到关键点响应图,关键点响应图表示关键点在各个位置上的置信度。显然,如果关键点在该位置上的置信度越高其对应的响应值也越大,所以对关键点响应图进行非极大值抑制操作便能得到关键点的准确位置。需要指出的是,关键点响应图的数目与选定的关键点数量相同,每个关键点响应图都对应着特定语义的关键点(如图8中的关键点响应图第一幅结果对应着主体上方左顶点)。通过这种方式,便使得由Hourglass网络提取到的关键点具有语义信息。因此,提取出语义关键点后便同时完成了特征提取和特征关联的操作,最后利用EPnP算法解算出目标的姿态。

图8 基于Hourglass网络的空间目标姿态估计的过程图Fig.8 Process diagram of space target pose estimation based on Hourglass network
3.3.1无降质情况下姿态估计结果对比与分析
下面给出利用本文方法进行姿态估计的定性结果图如图9所示。其中,图9(a)是输入图像,图9(b)是提取出的语义关键点,图9(c)是根据姿态估计值把目标对应的线框模型投影叠加在图像形成的结果。受篇幅限制,这里只展示了第一个关键点响应图(对应主体上方左顶点)的结果。

图9 空间目标姿态估计定性结果图Fig.9 Qualitative results of space target pose estimation
对实验结果从统计角度进行定量分析以评估算法性能优劣。设对目标三个姿态角(俯仰角、偏航角、滚转角)的估计误差分别为Δφ、Δθ、Δγ,而姿态真值和估计值对应的旋转矩阵分别为Rtrue和Rest,则选用总体姿态估计误差[18]作为误差评价指标,其定义如式(12)所示,其表征了三个姿态角估计误差的模距。
(12)
令平移量真值为ttrue,方法估计值为test,则平移量估计值的误差te为:
te=|ttrue-test|
(13)
为了客观度量本文姿态估计算法的性能,我们在3.1节所构造的仿真数据集上,不仅计算了本文姿态估计平均误差和平均消耗时间,还挑选了[12]和[19]两种具有代表性的基于特征关联解算姿态的方法进行比对。其中文献[12]使用的是点特征,基于ORB算子提取的轮廓点对图像和目标模型进行关联,进而求解出目标姿态;文献[19]使用了线特征,将观测图像中提取的直线特征与太阳能帆板结构进行关联,从而求解姿态的方法。在评价指标上,本文选用平均误差作为方法的评价指标,取所有测试样本估计误差的平均值作为最终的误差结果,实验结果如表1所示。
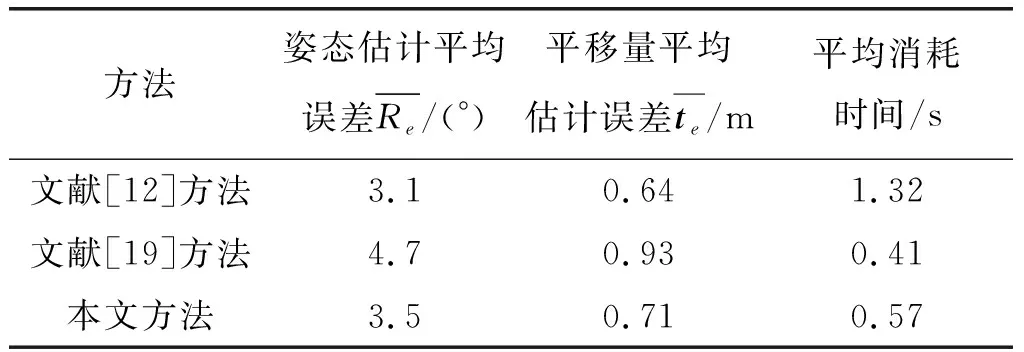
表1 三种方法的实验结果对比
从表中可以看出,文献[19]方法平均消耗时间最少,因为其只包含阈值分割和直线检测两个步骤,通过提取帆板直线特征然后建立特征关联,然而直线特征描述目标整体结构特征的能力有限,所以其准确率也最低,姿态估计平均误差为4.7°。为了提高姿态估计准确率,文献[12]通过构建候选空间的方法获得合适姿态初值,同时还提取复杂ORB特征描述子进行特征关联,虽然方法准确率较高,但其平均消耗时间为1.32 s,明显慢于其他两种方法,这说明该方法计算效率较低。本文通过提取语义关键点的方法同时完成特征提取和特征关联操作进而求解姿态,在获得了与文献[12]准确率相当的估计结果(姿态估计平均误差只相差0.4)条件下,其在计算效率上相比于文献[12]有明显的优势(算法平均耗时仅为其一半)。其原因在于,本文方法不需要进行模板匹配以构建候选空间的耗时操作。同时,相比于文献[19],本文方法姿态估计准确率上有较大的优势,并且仿真实验证明在理想条件下,其姿态估计最小误差为0.83°,这表明本文所提的语义关键点算法能反映目标整体结构。综上所述,本文方法相较于两种方法能兼顾算法的精度和效率。
3.3.2降质情况下姿态估计结果对比与分析
考虑太空实际观测环境的复杂多变性,观测图像往往因光照变化、高速运动等因素出现降质模糊,因此,我们进一步在3.1节所构造的实验仿真数据集上,加入不同程度的降质条件,从而进一步分析在降质情况下本文所提方法与前述两种方法的姿态估计性能变化情况。以“嫦娥一号”为例,其由光照和运动引起的降质情况示意图如图10所示。

图10 “嫦娥一号”图像降质情况示意图Fig.10 Images quality deterioration of “Chang’e-1”
下面再给出利用本文方法在降质条件下姿态估计的定性结果图如图11所示,图11(a)是输入图像,图11(b)是提取出的语义关键点,图11(c)是根据姿态估计值把目标对应的线框模型投影叠加在图像形成的结果。受篇幅限制,这里只展示了第一个关键点响应图(对应主体上方左顶点)的结果。与图9对比发现对图像进行降质后会对姿态估计结果产生一定影响。
下面测试本文方法在这两种典型的降质情况下的性能:对图像模糊性能测试时,利用式(14)的二维高斯函数对观测图像进行高斯模糊处理,高斯核半径设定为5像素,调节标准差σ从0.2到1,间隔为0.2;对光照变化性能测试时,调节光照相位角的范围从0°到90°,当光照相位角大于90°时,目标将不可见。测试结果如图12所示。

图12 图像降质性能测试结果图Fig.12 Performance result under images quality deterioration
(14)
在模糊性能测试中,三种方法的姿态估计误差随着高斯模糊标准差的增大而增大,说明图像模糊退化对所有方法均产生了影响;在没有降质前,即高斯模糊标准差为0时,本文方法与文献[12]姿态估计性能相当。但是,随着模糊的增强,文献[12]的平均姿态估计误差开始陡增。当高斯模糊标准差大于0.6时,本文方法明显优于文献[12]和文献[19](平均姿态估计误差最大相差10°)。
在光照变化性能测试中,随着光照相位角变大,姿态估计误差也增加,且光照变化对姿态估计任务的影响更大,在光照变化性能测试中,随着光照相位角变大,姿态估计误差也增加,且光照变化对姿态估计任务的影响更大,处在不同光照相位角下的目标如图13所示。需要指出的是,当光照相位角介于75°~90°之间时,目标主体大部分将不再清晰可见。在实际中,为了获得较稳健的估计结果,通常选择在稳定光照条件下(即保持目标主体基本可见)开展空间目标姿态估计任务。因此,本文的仿真实验中侧重对光照相位角在75°以内的情况进行分析。在理想光照条件下,本文方法与文献[12]姿态估计性能相当,当光照相位角大于45°时,即目标部分“淹没”在黑暗时,所有方法的估计误差都开始急剧增加,在复杂多变的光照条件下,与文献[12]和文献[19]相比,本文方法在准确率上有明显的优势(平均姿态估计误差最大相差20°)。

图13 不同光照相位角下的目标Fig.13 Targets under different illumination phase angles
文献[19]和文献[12]方法受图像降质影响较大,这是因为它们包含特征提取和匹配关联两个阶段,而图像降质会显著降低图像特征提取的可靠性,影响后续特征关联匹配的正确率,并最终影响姿态估计结果的准确性。本文方法则端到端地提取包含语义信息的关键点,直接实现了光学图像中二维特征点与目标三维实体结构的关联映射,所以受降质影响较小。综上所述,本文方法在降质条件下呈现出更好的鲁棒性和准确性。
4 结论
本文提出了一种基于语义关键点的空间目标姿态估计方法,在目标结构已知的前提下估计单幅光学观测图像中空间目标的三维姿态。本文所提的方法旨在解决太空特殊观测场景下特征提取性能受限而导致特征关联误差累积的问题,首先基于Hourglass网络提取出能反映目标整体结构的语义关键点,然后用EPnP算法求解获得目标姿态。实验结果表明,与其他主流方法相比,本文所提方法能较好地兼顾准确率和效率,并且对因太空特殊观测环境导致的图像降质表现出更好的适应性。考虑更多降质因素,进一步提升网络的泛化性能,是本文下一步工作的主要研究内容。

