基于响应面优化的堆石混凝土热学参数反分析

曾令福，邹 爽，陈兴梅，黄树新

(贵州大学土木工程学院， 贵州 贵阳 550025)

1 概述

堆石混凝土(Rock Fill Concrete，RFC)是一种基于自密实混凝土新兴的大体积混凝土，依靠自密实混凝土(Self-compacting Concrete， SCC)优良的自动密实功能填充堆石体间隙，将堆石体构造成密实、整体性好、强度较高的混凝土[1- 2]。目前主要运用于水利筑坝工程中，由于RFC中有较多大粒径的堆石(占到堆石混凝土总体积的55%左右，粒径范围300～1000mm)存在，使得热力学性能有区别于常规混凝土，混凝土热学参数取值对其温度场数值仿真分析结果精度密切相关，是混凝土温控防裂设计关键[3]。

RFC是一种非均质性较高的多相复合混合料，在数值模拟中，大多忽略RFC的非均质性，将其简化为均质各向同性的物体，在宏观上对其进行温度场及应力场数值仿真分析[4- 6]。采用简化方法可以方便建立有限元模型，但RFC各成分材料有不同的热学性能，模型的简化对温度场分析与实际情况存在差别。因此，需要选取能综合考虑各种因素，准确控制堆石混凝土热学性能的等效热学参数。

因其材料的特殊性，堆石混凝土热力学参数值难以用常规实验取得，由经验和理论推算所得参数与不能完全反映实际工程状况。依据实际工程监测资料建立数值模型对其热学参数进行反分析，是一种获取其参数的重要途径[7- 8]。

常用于参数反馈分析方法有神经网络、响应面法、遗传算法等。响应面方法由 Box 和Wilson[9]提出，此方法简单、可靠、操作性强，能较好地适应于解决非线性数据处理问题。Das[10]等人运用响应面模型，使数值模型的计算精度大幅提高。依据某堆石混凝土重力坝施工期实际温度数据，本文采用响应面法建立堆石混凝土热学参数与温度关系模型，根据响应面模型与实测数据建立反分析目标函数，并使用遗传算法搜寻最优组合参数，对堆石混凝土施工期热学参数进行反演分析，获取堆石混凝土的热学参数，验证此方法的合理性。

2 响应面法与优化计算

响应面方法(Response Surface Methodology，简称RSM)是近似模型的一种，是通过利用数值模型方法来逼近设计变量和响应变量之间的隐函数关系，创建响应面模型过程包括：样本数据采集、选择响应面近似模型和优化计算3步[11]。原理如下：

设y与设计变量x1，x2…xn之间的隐函数关系式为y=f(x1，x2…xn)，通过样本数据设计试验和待定系数法求得两者的近似函数模型，可表示为：

(1)

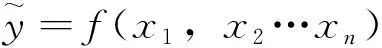
响应面近似模型只需要少量的试验样本点在小范围内就能比较准确地逼近因子和响应的函数关系，而且用简单的多项式表达出来，计算成本低，效率高。响应模型主要有一阶、二阶、三阶和四阶多项式，满足复杂的响应关系拟合，拥有良好稳健性[12]。

2.1 样本点设计

试验样本点可以来自试验设计、随机试验、物理试验等。目的是用来拟合设计因子和响应值之间的响应模型。经常使用的试验方法有中心组合设计(CCD， Central composite design)、正交设计(OA， Orthogonal arrays)、全因子设计(FFD， Full factorial design)等设计方法[13- 14]。本文采用由Box和Wilson提出CDD设计样本点，只需要较少的试验组数，通过变量因子的评估，用响应值可各因子优化，进而得到符合响应值的最佳组合值[6，15]

对于不同个数的试验因子，其试验样本数与因子个数之间的关系见表1。

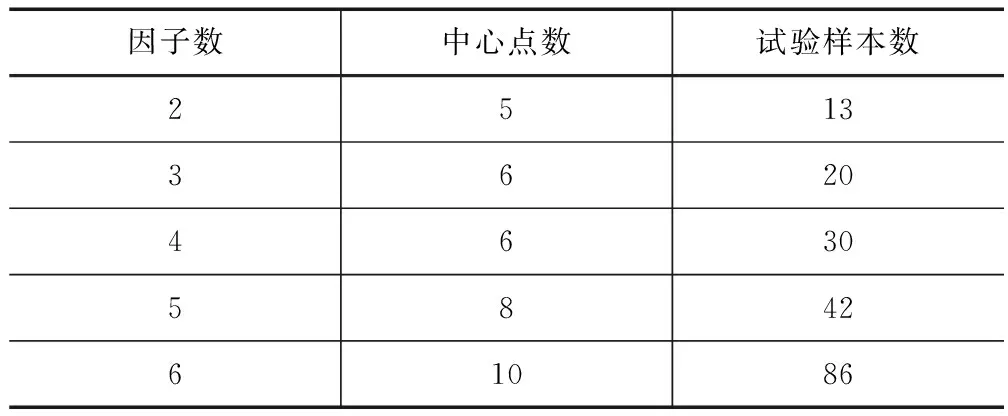
表1 中心组合设计因素与试验次数

本文选取二阶多项式函数拟合设计空间，二阶多项式响应面函数模型如下：

(2)

式中，y—响应值；xi、xj—试验参数物理量；α0、αj、αij—待定系数。

2.2 优化算法

本文选取遗传算法(Genetic Algorithm，GA)为目标函数进行优化计算，遗传算法是摹拟生物在自然环境中遗传繁殖机制以及进化规律演变而成的全局优化搜寻方法[16]。遗传算法在进化搜寻中自动获取和积累有关搜查空间的知识，无须借用外界信息，只凭借评价函数值作为搜寻依据，遗传过程根据评价函数值的大小评判可行解能否繁衍，评价函数值大的可行解能得到繁衍机率比评价函数值小的可行解大，保证了新解集的平均评价值大于旧解集的平均评价值。评价函数设计如下：

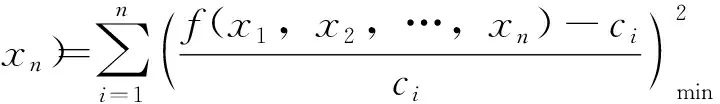
(3)

式中，F(x1，x2，…，xn)—评价函数；x1，x2，…，xn—可行解；f(x1，x2，…，xn)—近似数值函数模型计算值；ci—实际监测值。

为避免寻优不收敛，同时较少计算量，通过施加约束条件以提升计算速率，约束函数如下：

(4)

式中，ε—待优化问题的精度。

3 工程实例

某堆石混凝土重力坝强度等级为C9015，最大坝高30.80m，坝轴线长86.0m，顶高程1106.30m。河床段坝及左右坝肩基置于弱风化基岩上，河床高程1075.50m，坝基基础设置1m厚二级配C15常态混凝土垫层，上游面设有0.5m厚的自密实混凝土防渗层。将堆石混凝土看作是均质材料模型，第一仓堆石混凝土浇筑高程为1076.5～1078.5m，在坝断面0+048高程1077.5m处埋设有温度计T1-T3，温度计测点位置如图 1所示。

图1 温度监测位置

堆石混凝土底宽26.6m，顶面宽24.6m，每仓浇筑厚2m，左右取厚度的2.5倍，即5m，上游设置了厚0.5m的C15自密实混凝土防渗层，从而建立三维有限元模型，选用SOLID186单元定义材料，上游自密实混凝土防渗层单元尺寸为0.2m，堆石混凝土单元为0.4m，C15垫层单元尺寸为0.4，共划分13620个单元，66682个节点，首仓堆石混凝土计算模型如图 2所示。

图2 首仓堆石混凝土有限元模型

使用有限元软件的瞬态热分析计算温度场，堆石混凝土入仓温度为8℃，上下游面与钢模板接触，顶面采用第三类边界条件定义，结构内部热源主要为堆石混凝土水泥水化放热，堆石混凝土绝热温升采用指数式定义，m值取0.445。坝体各材料热学参数见表2。

在进行有限元模型计算时，堆石混凝土材料热学参数采用表2中的经验值计算温度场时，计算温度值与工程实际监测温度值存在较大差异，说明堆石混凝土热工参数经验取值与不符合实际情况。因此，需要依据实际监测温度值获取堆石混凝土热学参数。

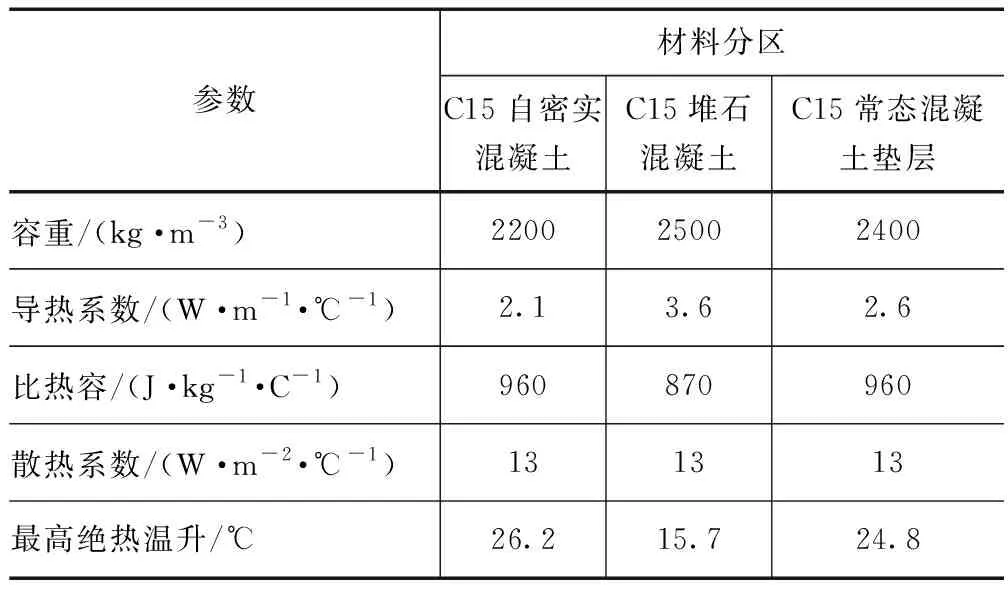
表2 材料参数取值

3.1 热学参数敏感性分析

混凝土内部不同龄期、位置的温度对热学参数敏感性不同，敏感性分析的作用是探究系统参数在细微变动时温度响应值的变化情况，排除影响不显著因子，减少试验计算量的同时提高近似模型的精确度。首先对堆石混凝土的4个热学参数进行CCD试验设计，即最终绝热温升、比热容、导热系数、及空气中表面散热系数，以第一仓堆石混凝土里面T2监测点的温度作为响应值。4因子设计30个试验样本，使用ANSYS计算各组试验样本的响应温度值，选用浇筑后第1、3、5d 12:00的温度值T21、T23、T25作为响应值。该试验样本计算见表3。

通过方差分析方法，设置各热参数显著性为0.05，依据响应面显著性判定标准来判断各热学参数对不同时间温度值响应的敏感程度。当热工参数P-Value小于0.05且越趋于0时，表示此热学参数对温度响应值的影响越大。反之，各热学参数P-Value值大于0.05且越大时，对其温度的影响越小。为使响应模型简单精准，通过该判定准则，对各热学参数的灵敏度进行显著性分析，排除影响不显著因子以提高模型的精度和质量。其各项热参数对温度响应值的灵敏性如图 3所示。

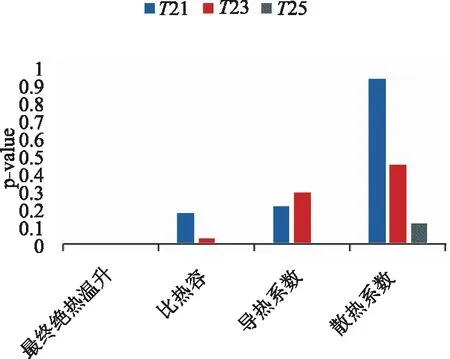
图3 参数显著性

通过各参数显著性分析可知，散热系数对结构内部T2测点1、3、5d影响都不显著，其余3个热学参数对温度响应都有不同程度的影响，因此，选取最终绝热温升、比热容和导热系数进行参数反分析。

3.2 响应面拟合

选取最终绝热温升、比热容和导热系数进行响应面模型拟合，使用3因素3水平的中心组合试验法设计20组试验参数，重复中心点6次。运用ANSYS软件计算各参数组情况下堆石混凝土温度值，选用第1、3、5d 12:00计算温度值作为反分析参数的响应，堆石混凝土热学参数取值区间见表3。

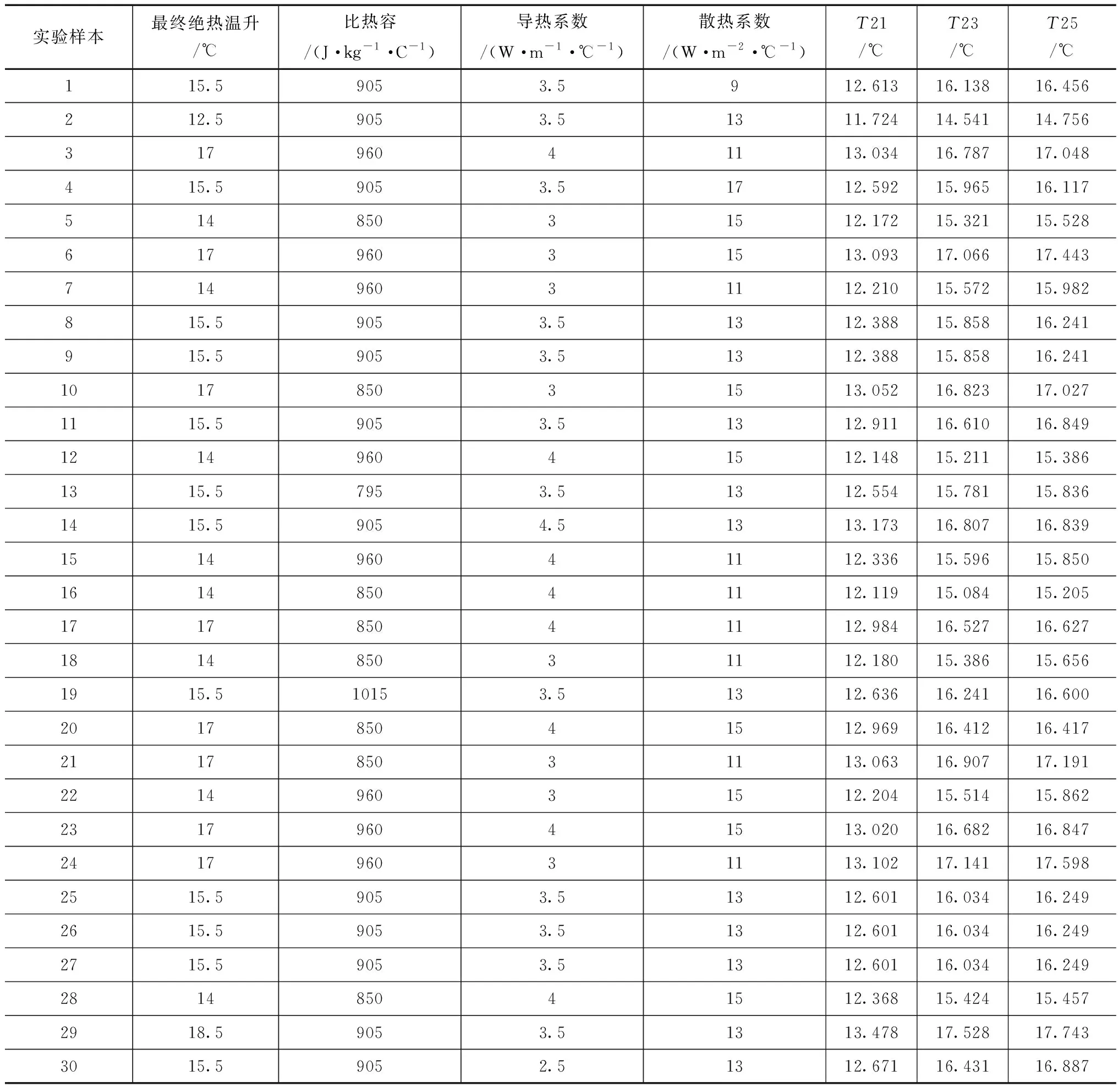
表3 试验样本

采用公式(2)进行响应面拟合，记最终绝热温升为A，比热容为B，导热系数为C。二阶多项式拟合的响应面数值模型如下：

T21=8.49328+0.39026×A+2.09769-3×

B-1.33233×C+9.24242-5×A×B

-0.042333×A×C-1.0-4×B×C

-1.46825-3×A2-1.58796-6×B2

+0.30779×C2

(5)

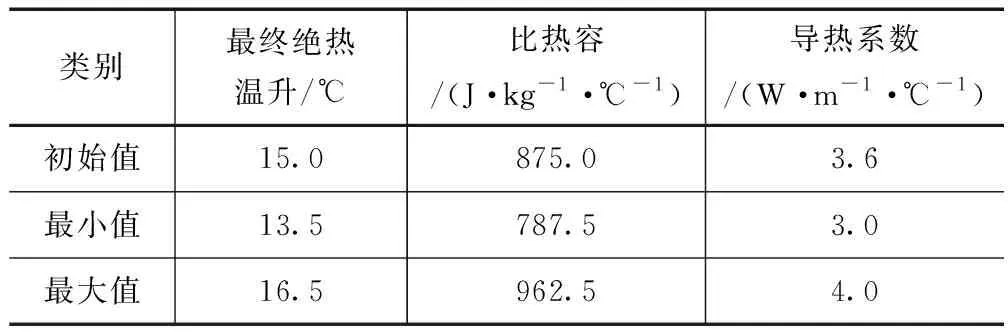
表4 参数取值区间

T23=2.33954+0.84975×A

+0.014464×B-2.19226×C

+2.49242-4×A×B-0.087583×A×C

-6.13636-5×B×C-9.37698-3×A2

-8.91677-6×B2+0.50011×C2

(6)

T25=3.38999+0.99390×A+0.023754

×B-1.97962×C+3.33333-4×A×B

-0.099167×A×C-1.31818-4×B×C

-0.015143×A2-1.38666-5×B2

+0.47721×C2

(7)

利用相关系数R-Squared、Adi R-Squared 及 Pred R-Squared 来评估模型拟合的精度。由表可看出，温度响应数值模型的拟合精度高，表明建立的温度响应面模型能够较好地表示出热学参数变量值与温度响应变量值之间的隐式函数关系。

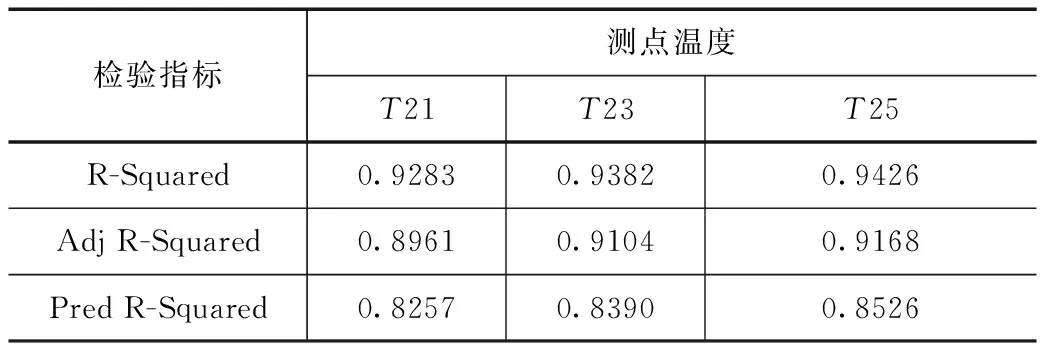
表5 拟合精度检验

3.3 求解反分析参数

依据响应面函数与工程实测温度值的差值平方和最小构造寻优目标函数如下式：

(8)

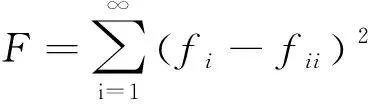
采用遗传算法进行优化求解，根据响应面函数模型，以达到目标函数最小值为优化求解目标，使反演参数得到最佳组合值，参数反分析结果见表 6。

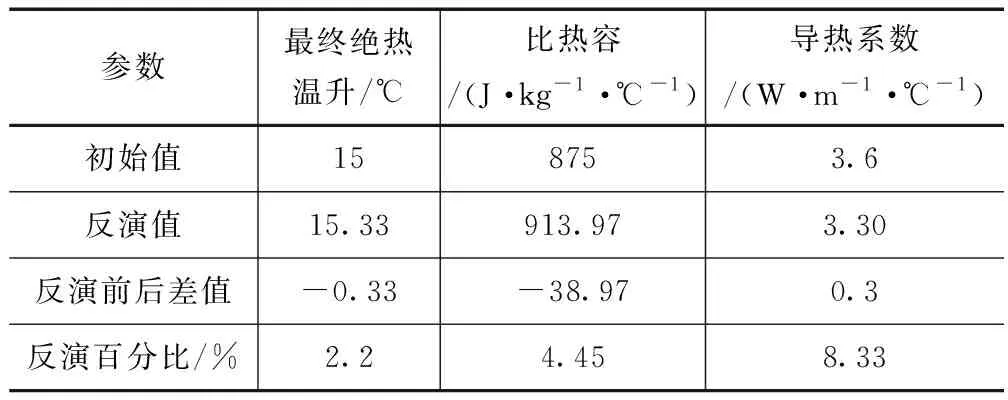
表6 反分析求解结果

根据反分析得到的优化参数对该仓堆石混凝土的进行有限元正分析，得到各测点各时的温度数据，并将反分析后参数计算的温度值与实测温度值对比见表7。

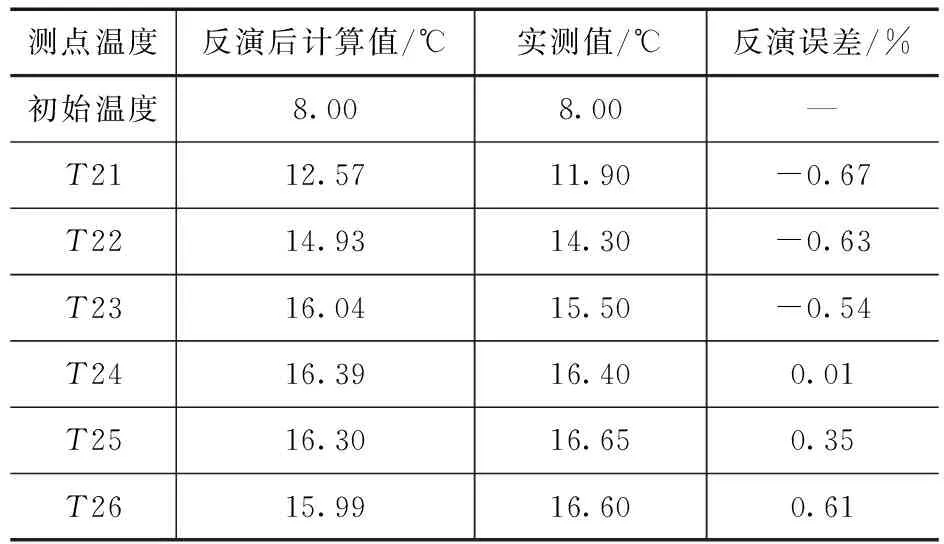
表7 反分析计算值与实测值对比

由表7可知，将反分析所得带入有限元计算后，堆石混凝土测点温度计算值与实际监测温度值基本吻合，反演误差在±1%内，T1测点有限元计算值与工程实际监测值如图 4所示。

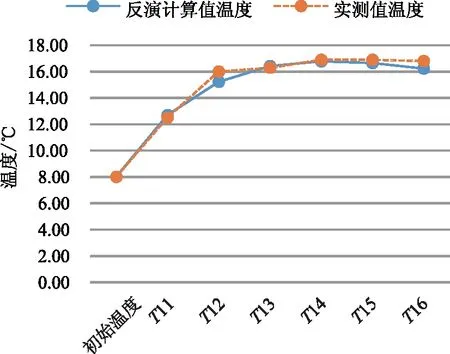
图4 T1测点计算值与实测值比较

由图4可知，测点T1的实测温度与对应的有限元计算温度值基本吻合，说明基于响应面技术反演分析堆石混凝土热学参数能表征其真实的热学性能，运用参数反演优化所得参数进行数值仿真可对堆石混凝土坝的设计施工提供一定的参考作用。

4 结论

(1)本文利用响应面模型理论，对堆石混凝土坝首仓内部测点T2进行参数敏感性分析，剔除了堆石混凝土表面空气散热系数影响不显著，符合经验认知。

(2)利用响应面方法，选取最终绝热温升、比热和导热系数建立能够反映出温度和参数之间隐式关系的响应面模型，根据拟合响应面模型相关评价指标，能够看出响应面数值模型具有较高精度。

(3)依据响应面模型建立了反分析目标函数，对堆石混凝土热学参数反演分析，得出相关的热学参数：即最终绝热温升为15.33℃，比热容913.97J/(kg·℃)，导热系数为3.30W/(m·℃)，将反演参数输入有限元正分析模型，得出测点有限元计算与实测温度基本吻合。计算表明，利用响应面法得到热学参数是可靠的，反演所得堆石混凝土热学参数值可为堆石混凝土坝的设计施工及裂缝预防提供参考。