Tunable optomechanically induced transparency and fast–slow light in a loop-coupled optomechanical system∗
Qinghong Liao(廖庆洪),Xiaoqian Wang(王晓倩),Gaoqian He(何高倩),and Liangtao Zhou(周良涛)
1Department of Electronic Information Engineering,Nanchang University,Nanchang 330031,China
2Key Laboratory of Opto-Electronic Information Acquisition and Manipulation of Ministry of Education,Anhui University,Hefei 230601,China
Keywords:hybrid optomechanical system,optomechanically induced transparency and absorption,normal mode splitting,fast light and slow light
1.Introduction
A cavity optomechanical system(COMS),[1,2]which describes the interaction between the mechanical resonator and the light via radiation pressure,has brought significant development in many different areas of physics.It is widely acknowledged that the COMS possesses diverse potential applications,such as quantum entanglement,[3,4]NMS,[5–7]ground-state cooling of mechanical modes,[8–11]electromagnetically induced transparency(EIT),[12–17]and optomechanically induced absorption(OMIA)[18]phenomena,etc.To a large extent,it promotes the development of photon transmission and quantum information processing.OMIT is a typical example of light-control light via mechanical motion.[5,19,20]Analogous to EIT,the OMIT resulting from the destructive interference of the anti-Stokes scattering field and the weak probe field plays an essential part in quantum information and communication processes.[21–24]In theory Agarwal and Huang have discovered that the optomechanical system becomes transparent to a weak detection field at resonant point when a strong pump field is applied to drive the optical cavity.[25–27]Furthermore,it has been also sequentially confirmed in experiments[28,29]and has received much attention in a hybrid COMS,[27]a quadratically coupled COMS,[26–30]a spinning COMS,[31]and in a parity-time symmetric microcavity system,[32,33]etc.Physically the phenomena of OMIA is also predicted in a hybrid optomechanical system.[18]
Due to the narrow transparency window accompanying with the abnormal dispersion,the most outstanding application of OMIT is considered as storage and light delay.[34–37]In the last few years,what has interested us extremely is the study on fast–slow light effect.[38–41]Various techniques have been developed to realize fast–slow light.One method is the use of the EIT technology,a quantum interference effect that can produce the dramatic change of the absorption and dispersion properties.Thus,the nonlinear susceptibility is enhanced and slow light is generated.[42,43]Akram et al.[44]have studied the fast and slow light effects in a hybrid COMS based on EIT technology.Another application among these ways is to control the group delayτof light pulses,[45]resulting in slow light(τ>0)and fast light effects(τ<0).Many schemes for studying fast–slow light have been proposed in the COMS.For instance,Zhan et al.[43]have observed that slow light can be achieved over an extensive range of parameters even at high temperature such as 200 K in a quadratically coupled COMS.Akram et al.[44]have found that adding atom–field coupling into the hybrid system can further enhance the fast light effect obtained by single optical-mechanical coupling.Additionally,the conversion between fast light and slow light has been done under the action of an external force.[46]It is reported that the transmitted probe beam can be delayed as much as 4µs and can be easily controlled by the power of the pump beams in a two-mode COMS.[47]More recently,Macke et al.[48]have found that both slow and fast light can be obtained by selecting particular phase components of the transmitted field in a zero-dispersion configuration.And Chen et al.[49]have observed that a tunable and controllable fast-to-slow light propagation can be achieved by controlling the driving amplitudes and phase of the phonon pump.In parallel,the research of the multiple-mode optomechanical systems has attracted much attention and many quantum phenomena have been studied in recent years.Xu et al.[50]have found that the EPs periodically emerge and the sidebands’spectrum can be modified significantly by tuning the relative positions of the nanotips.Hao et al.[51]have indicated that the controllable amplification of the probe light can be achieved,which is induced by the constructive interactions of photon,atom,and phonon.It has been determined that tuning the OPA parameters can considerably suppress quantum back-action noise and enable the device to reach sub-SQL sensitivity.[52]Furthermore,the sensitive impacts of the dark mode effect on the optical properties in a three-mode loop-coupled optomechanical system have been proposed in Ref.[53].Besides,Liu et al.[54]have investigated the squeezing transfers from a squeezed vacuum injected in one cavity to the output spectrum of the other cavity in the two-cavity optomechanical system.Lai et al.[55]have found that the ground-state cooling of the two mechanical resonators can be realized simultaneously under the optimal driving detuning and in the resolved-sideband regime.
Motivated by these developments,we theoretically consider a circular hybrid model,[3,56]where two optical cavities are coupled to a common mechanical resonator identically.[57–59]At the same time,the two optical cavities interact with each other through photon-coupled paths.The present work has the following distinct features:Firstly,the photon coupling strengths and related parameters can be precisely adjusted to realize controllable photon transmission.Secondly,we propose a pump–probe optical method to detect tunnel coupling strength.Thirdly,the conversion between slow light and fast light can be achieved by adjusting a variety of paths,which provides an excellent platform for the modulation of fast light and slow light.
The main research content is as follows:In Section 2 we give out the model of the hybrid COMS considered in our work and calculate the amplitude of the output corresponding to the weak probe analytically.In Section 3,we discuss the OMIT(OMIA)and give the explicit explanation for the mechanism.Furthermore,we study the influence of different factors on OMIT.A conversion between OMIT and OMIA adjusted by related parameters is emphasized.In Section 4,the group delay of the output field is also investigated.Finally,we present our conclusions in Section 5.
2.Theoretical model and solutions
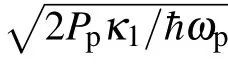
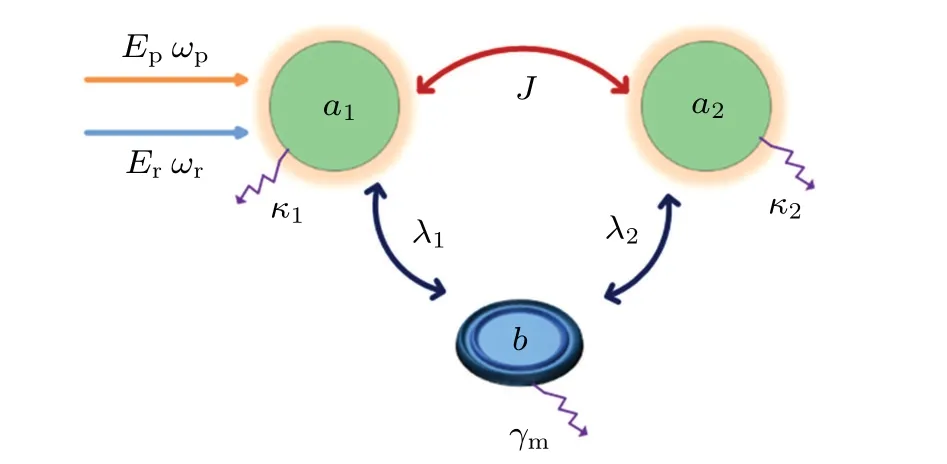
Fig.1.Schematic diagram of the loop-coupled hybrid optomechanical system composed of two optical cavities coupled to the same mechanical resonator.The two cavities are coupled directly with intercavity coupling strength J.The system is driven by a strong pump laser and a weak probe laser.
Introducing the rotating wave approximation at the pump frequencyωp,the effective Hamiltonian of the system reads[61,62]
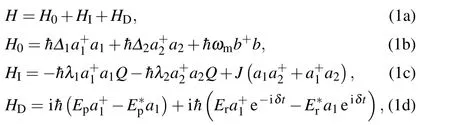
withδ=ωr−ωp.Here,H0represents the free Hamiltonian of the system,where aiand b are the annihilation operators describing the optical fields and the mechanical resonator,respectively.The frequency of the mechanical resonator isωmandΔi=ωci−ωpgives the detuning between the cavities(ωci)and the optical drive(ωp)frequencies.The second term HIdefines the interaction Hamiltonian.Cavity fields are coupled to the mechanical resonator via the linear optomechanical couplingλi(i=1,2).J is the coupling strength between the two cavities.The final term HDdescribes the interaction Hamiltonian between the optomechanical system and the control field as well as the probe field.
Based on the Hamiltonian in Eqs.(1a)–(1d),the Heisenberg equations including the corresponding noise and damping terms can be given by(¯h=1)
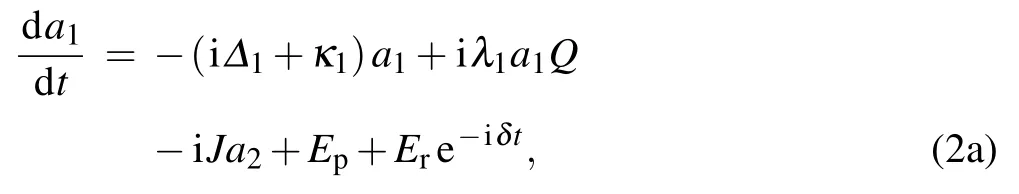
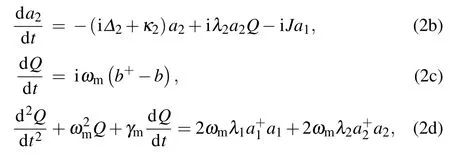
whereγmis defined as the decay rate of the mechanical resonator.The following ansatz is adopted to solve the Eqs.(2a)–(2b):

Substituting Eqs.(3a)–(3c)into Eqs.(2a)–(2d)and ignoring all the small-terms multiplication as well as the secondorder terms,we obtain
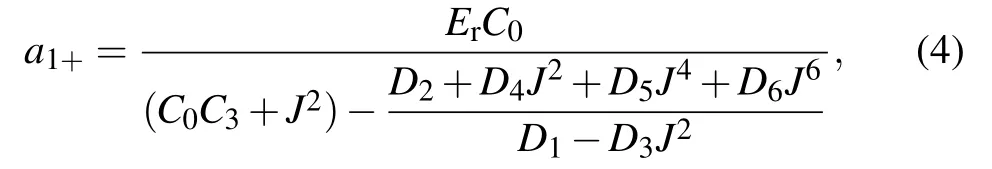
where

with
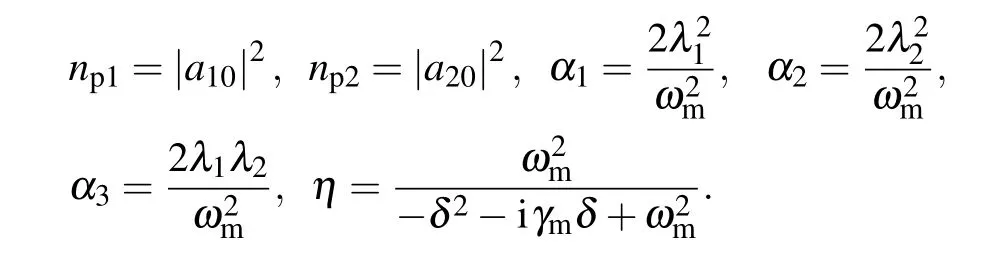

In general,the real part Re(εout)represents the absorption behavior and the imaginary part Im(εout)describes the dispersion properties of the probe field.[65]Furthermore,for a COMS,the rapid phase dispersion can cause the transmission group delay in the region of the narrow transparency window,which is confirmed as
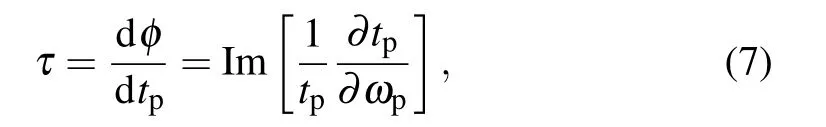
3.Optomechanically induced transparency and absorption in the loop-coupled hybrid optomechanical system
In the previous section,we derive the analytic results of the system evolution.In what follows,we numerically illustrate the dependence of the absorption properties of the probe field on the probe–cavity detuning for different system parameters.In order to better comprehend the response of the system to the probe field,the parameters realizable experimentally are chosen as[10]ωm=2π×947 kHz,ωc1=ωc2=1.77×1012kHz,γm=2π×0.14 kHz,κ=κ1=κ2=2π×215 kHz,andλ=λ1=λ2=250 Hz.
First of all,we seriously discuss the absorption of the probe field affected by different tunnel coupling strengths in Fig.2.If two passive optical cavities are weakly coupled for J<κ,the photon exchange rate is slower than the cavity fields decay rate and there only appears a shallow transparency window aroundΔr=0.At this time,the absorption spectrum behaves like OMIT characteristic in a single-mode COMS,where the normal modes are not split and the absorption spectrum of the probe field is mainly caused by the optomechanical interactions.Specifically,the sideband absorption peaks decrease with the increase of tunnel coupling strength J.When the coupling strengths are increased up into the strong regime,i.e.,J>|κ1+κ2|/2=κ,the photons exchange before the cavity field decays.We obtain that the absorption of the probe spectrum becomes distorted and splits into two normal modes.This is due to the fact that with the increase of J,the interaction between the two cavities plays a dominant role,which disturbs the absorption spectrum.Compared with Fig.2(a),it should be pointed out that there exists a rapid transition from absorption dip to peak and at the resonant point in Fig.2(b).We achieve double transparency windows which are produced by the strong tunnel coupling and the effective optomechanical coupling strengths between the two cavities and the mechanical resonator.Our numerical results also show that the absorption profile reverses from the peak to the dip atΔr=0 when the tunnel coupling is satisfied J=4κ.This indicates that the conversion from absorption to amplification can be achieved by adjusting tunnel coupling strength.Specifically,the sideband peaks of absorption appear respectively on the two sides ofΔr=0.The distance of the sideband peaks depends linearly on the tunnel coupling J while the heights of them show inversely proportional to J as illustrated in Fig.3.Therefore,it provides a simple and effective method to measure the tunnel coupling strength by just measuring the distance between the two sideband peaks.
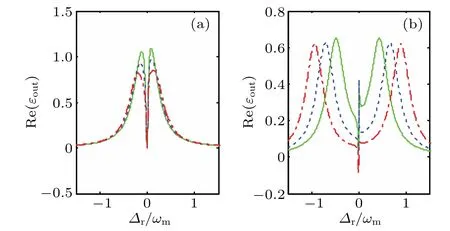
Fig.2.The real part of the output field Re(εout)as a function of the probe–cavity detuningΔr/ωm with different tunnel coupling values.(a)The weak tunnel coupling is given by J=0.4κ(green solid line),J=0.6κ(blue dashed line),J=0.8κ(red dashed-dotted line).(b)The strong tunnel coupling is set as J=2κ(green solid line),J=3κ(blue dashed line),J=4κ(red dasheddotted line).The corresponding parameter is Ep=4πkHz.

Fig.3.(a)The logarithm of the heights of two side peaks of absorption varies with the tunnel coupling strengths.(b)The logarithm of the distance between the two side peaks of absorption as a function of the tunnel coupling strength.Other parameters are the same as those in Fig.2.
In the following,we shall research the effects of the strong pump field with different values when the tunnel coupling is chosen as J=2κ.As we known,the effective optomechanical coupling can be enhanced by increasing the driving strength,which can lead to the increase of the mean photon number.In Fig.4(a),there are two asymmetric sideband peaks.Moreover,the left absorption peak is higher than the right one.Besides,the heights of the two asymmetric absorption peaks is proportional to the driving strength.When the driving strength becomes larger,the left absorption peak moves further away from the resonant point,whereas the right one becomes closer to the point of resonance.In the case of the resonant point,we can see clearly that the absorption is turned into amplification slightly as the driving strength increases.This can be explained by the interaction between photons and phonons.And the quantum interference between the Stokes field and the detection field results in the amplification effect.When the driving amplitude continues to increase,the switch from absorption to amplification appears.As shown in Fig.4(b),it keeps absorption state for Ep=17.08 kHz but turned into amplification for Ep=17.1 kHz.Due to the stability condition,there exists a critical value for the driving intensity.Further,the absorption properties are very sensitive to the driving strength atΔr=−ωm.This boundary point gives an idea to get unilateral models for amplifiers.

Fig.4.The real part of the output field Re(εout)as a function of probe-cavity detuningΔr/ωm for different driving strengths:(a)Ep=4πkHz(green solid line);Ep=8πkHz(blue dashed line);Ep=12πkHz(red dasheddotted line);(b)Ep=17.08πkHz(black dashed line);Ep=17.1πkHz(pink dashed-dotted line).
Next,we plot the probe absorption spectrum as a function ofΔr/ωmfor different decay rates of cavities in Fig.5.It is found that the distance between the two sideband of the absorption peaks gets larger with the increasing of the cavity decay.Meanwhile,the sideband peaks of absorption decrease.Likewise,amplification phenomenon can still be found and becomes more obvious with the increase of decay rate.
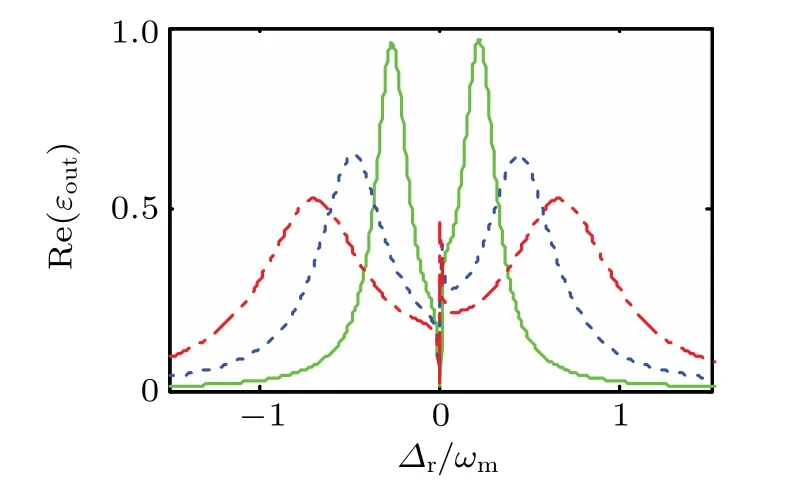
Fig.5.The real part of the output field Re(εout)as a function of probe–cavity detuningΔr/ωm with differentκ:κ=π×215 kHz,κ=2π×215 kHz,κ=3π×215 kHz for green solid line,blue dashed line,and red dasheddotted line,respectively.The other parameters are the same as those in Fig.2.
4.The fast–slow light effects in the loop-coupled hybrid optomechanical system
We have investigated the optomechanically induced transparency and absorption of the loop-coupled hybrid optomechanical system.In what follows,we illustrate the group delay of the probe light as a function of the probe–pump detuningδ with different tunnel coupling J,using the same parameters as in the previous section.Now,we consider the phase dispersion curves of the output probe field.The rapid phase dispersion can generate the transmission group delay.It can be seen clearly from Fig.6(a)that there is a transparency window combined with a steep negative phase dispersion at the resonant point,which will result in a tunable group delay of the transmitted probe beam.[47]From Fig.6(b),we obtain that the group delay is positive with a maximum value of 0.57 ms when the tunnel coupling strength is J=1.5κ.Further,in the region J>2.5κ,the group delayτbecomes negative.The reason for these interesting phenomena is that the fast–slow light effects of the transmitted probe field depend on the phase dissipation of the transmitted probe field,and the phase of the transmitted probe field suffers a fast shift with the change of the tunnel coupling strengths.Therefore,as long as the appropriate value ofωmis selected and the value of J is slightly changed,the regulation of fast and slow light can be realized.
Then,in order to further investigate the effect of optomechanical coupling strengthsλon the fast light and slow light,we present the group delay in Fig.7.It can be seen by dashed(λ=250 Hz)and dashed-dotted(λ=375 Hz)curves that the switch between fast light and slow light will occur at the resonant point.Also,the group delay can be further enhanced with different optomechanical coupling strengths and the optimal location moves to left with the increase of the optomechanical coupling strengths.In the hybrid optomechanical system,the pulse advancement can be increased by continuously increasing the optomechanical coupling under a constant tunnel coupling.Hence,we can achieve the high phase dispersion which leads to the higher pulse advancement by employing both coupling parameters.
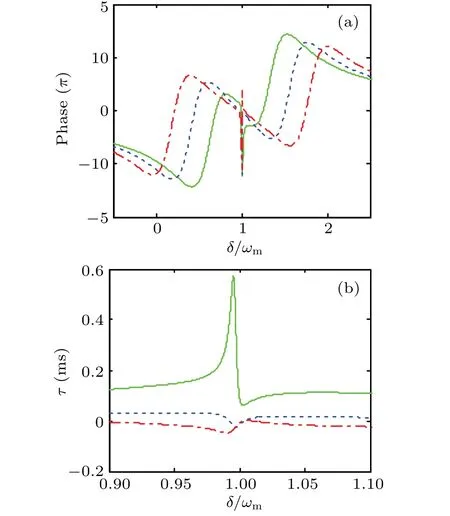
Fig.6.(a)Phase of the transmission and(b)group delayτas a function ofδ/ωm for different tunneling amplitudes:J=1.5κ(green solid line),J=2.5κ(blue dashed line),J=3.5κ(red dashed-dotted line).We use the other parametersλ=250 Hz,κ=2π×215 kHz.
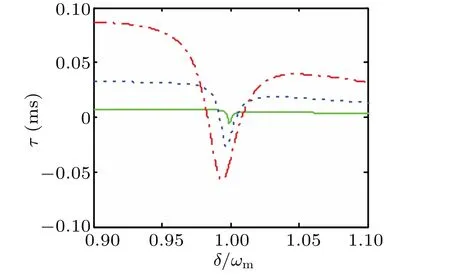
Fig.7.Group delayτas a function ofδ/ωm for different optomechanical coupling strengths:λ=125 Hz(green solid line);λ=250 Hz(blue dashed line);λ=375 Hz(red dashed-dotted line).Other parameters are the same as those in Fig.6 besides J=2.5κ.
Next,it is natural to wonder how this group delay behaves whenλ1/=λ2.Here,we defineξ=λ1/λ2.Figure 8 shows that the output of the probe field maintains slow light in the region of 1<ξ<4,but a conversion from slow light to fast light appears atξ=4.45.Our numerical results also manifest that,whenξ>6,the influence ofξon group delay gradually stabilized.Meanwhile,the fast light manifests more obviously.From this figure,we can see that the effect ofξon group delay is mainly concentrated in 4<ξ<6.Therefore,the tunable slow and fast light effects can be easily realized by adjusting the optomechanical coupling strengths in this optomechanical system.
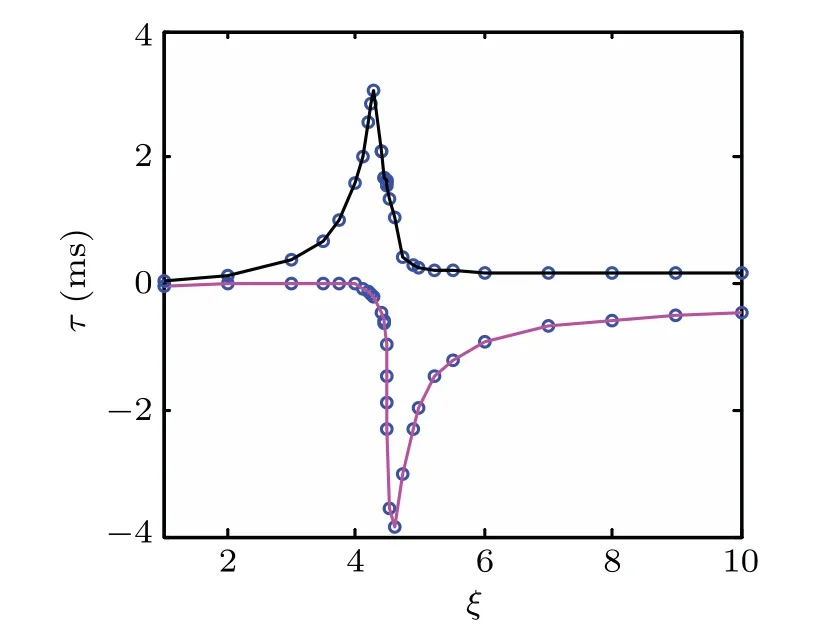
Fig.8.The maximum(black line)and minimum(pink line)of group delayτ as a function ofξin the region ofδ≈ωm.Other parameters are the same as those in Fig.7.
Finally,it would be interesting to study the influence of the driving strengths Epon the output field group delay which is induced by the mechanical resonator.In Fig.9,we can see clearly that the group delay converts from positive to negative values and tends to be stable whenδ/ωm>1.05.We find that the group delay dip becomes shallower and narrower with the decrease of driving strengths.As the driving strength increases,the group delay dip moves further from the resonant point and the group delay is enhanced.At this time,it is accompanied by the transition between fast and slow light.So the adjustability of group delay caused by quantum interference between the probe field and the anti-Stokes field[67]can be dynamically adjusted by controlling the driving field strengths.
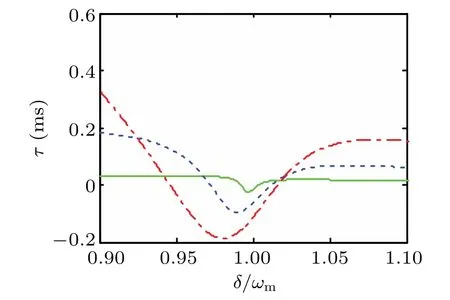
Fig.9.Group delayτas a function ofδ/ωm for different driving strengths:Ep=4πkHz(green solid line);Ep=8πkHz(blue dashed line);Ep=12πkHz(red dashed-dotted line).The other parameters are the same as those in Fig.6 besides J=2.5κ.
5.Conclusion
In conclusion,we have investigated the optomechanically induced transparency of the loop-coupled hybrid system that composes of two optical cavities coupled to a common mechanical resonator for different tunnel couplings.Both OMIT generated by optomechanical interactions and NMS caused by the strong photonic coupling can be observed in this study.We also observed that the amplification phenomenon can occur under the combined action of the optomechanical coupling and the strong tunnel coupling.Furthermore,the intensity and distance of the sideband absorption peaks can be controlled by selecting appropriate parameters.Our research indicates that the conversion between slow light and fast light can also be achieved by modulating optomechanical coupling strengths appropriately.Moreover,the group delay can be enhanced by manipulating the optomechanical coupling strengths.These optical response characteristics can be used to realize the fabrication of optical devices such as the full-photon switch and have a broad application prospect in high-precision measurement and macro-quantum phenomenon research.
- Chinese Physics B的其它文章
- Origin of anomalous enhancement of the absorption coefficient in a PN junction∗
- Protection of isolated and active regions in AlGaN/GaN HEMTs using selective laser annealing∗
- First-principles study of plasmons in doped graphene nanostructures∗
- Probing thermal properties of vanadium dioxide thin films by time-domain thermoreflectance without metal film∗
- An improved model of damage depth of shock-melted metal in microspall under triangular wave loading∗
- Signal-to-noise ratio of Raman signal measured by multichannel detectors∗

