Detection of multi-spin interaction of a quenched XY chain by the average work and the relative entropy∗

Xiu-Xing Zhang(张修兴),Fang-Jv Li(李芳菊),Kai Wang(王凯),Jing Xue(薛晶),Guang-Wen Huo(霍广文),Ai-Ping Fang(方爱平),and Hong-Rong Li(李宏荣),‡

1Department of Physics,Weinan Normal University,Wei’nan 714099,China

2School of Physics,Xi’an Jiaotong University,Xi’an 710049,China

Keywords:nonequilibrium thermodynamics,spin chain,multi-spin interaction

1.Introduction

In recent years,quantum thermodynamics has become a thriving research field.[1–12]The theory of quantum thermodynamics aims at investigating how the concepts of heat,work and temperature can be extended to the quantum realm.It provides us the opportunity to understand the microscopic foundations of the laws of thermodynamics.In addition,it also spurs the designation of various quantum thermal devices,such as quantum heat engines,[13–19]quantum refrigerator,[20–22]and quantum batteries.[23,24]

At present,much focus has been put on the investigation of thermodynamics in the quenched quantum systems.[25–38]On the one hand,with help of ultra-cold atomic techniques,one can measure the probability distribution of work done on quenched gases of two-level systems.[39,40]These experimental results stimulate researchers’interest in the quenched systems.On the other hand,following a quench the quantum fluctuations will be generated,which has enriched the system’s phase diagram.[41,42]Thus,thoroughly investigating the critical behavior of a quenched system may open up a deep underlying connection between the quantum phase transition(QPT)and the quantum thermodynamics theory.Along this line,many works have been carried out.[34–37]Dorner et al.[34]investigated thermodynamics in a quenched transverse Ising model and found that the irreversible entropy production exhibits sharp peaks near the critical point.In Ref.[35],the work statistics has been studied in the quenched anisotropic XY model.It shows that the work fluctuation exhibits nonanalytical behavior when the quench is done across quantum critical point.Wang and coworkers[37]investigate the influence of the DM interaction on the nonequilibrium thermodynamics in the XY chain.Their results indicate that the critical behavior induced by the DM interaction can be revealed via the behavior of the work statistics and the irreversible entropy production.Moreover,it is also found that the work statistics in the vicinity of criticality is connected to the critical Casimir free energy.[43,44]

In the previous studies of nonequilibrium thermodynamics in spin chain systems,only the nearest-neighbor spin interaction is considered.[26–28]Besides the two-spin kind of interactions,however,multi-spin interactions may also exist in spin chains.[45–48]It has been proved that the phase transition points can be changed by the multi-spin interaction.[48]Consequently,some physical quantities,such as the entanglement,the quantum discord and the geometric phase,exhibit singular properties at the phase transition point.[48]A question then arises:how can we detect the multi-spin interaction in a spin system?Moreover,it has been shown that the average work changes greatly around the phase transition points of the spin system and can signal out the appearance of phase transitions.According to this point,the average work is expected as a detector of phase transitions in the nonequilibrium systems.[34–37]With the same reason,we expect that the average work and relative entropy may be used to detect the multi-spin interaction in the quenched systems.Starting from this point,we here investigate the nonequilibrium thermodynamics in the spin chain system,in which both the nearestneighbor spin interaction and the three-spin interaction are included.We analytically evaluate the statistical properties of the average work and the relative entropy under different sudden quenching parameters.The results show that the average work and the relative entropy can be used as the detector of the multi-spin interaction in the nonequilibrium system.Furthermore,the QPT that occurs in the nonequilibrium process can also be revealed.

The rest of this paper is organized as follows.In Section 2,we briefly review some key concepts about the nonequilibrium thermodynamics.In Section 3,the XY spin chain with multi-spin interaction is diagonalized and the characteristic function is obtained.In Section 4,main results and related discussions are presented.A summary is given in Section 5.

2.Nonequilibrium thermodynamics

In this section,we will review the key concept about the nonequilibrium thermodynamics and the formalisms that will be used in the rest of this paper.We consider a quantum system,whose initial state can be described by the Gibbs state

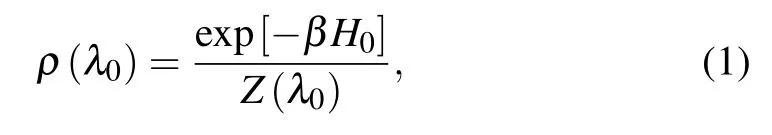
whereλ0is the initial value of the system parameterλ;Z(λ0)=Tr[exp[−βH0]]is the partition function;H0corresponds to the initial system Hamiltonian;andβ=1/T(kB=1)is the reciprocal temperature.

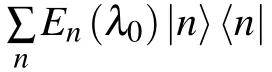
The work distribution of this non-equilibrium process is[9]

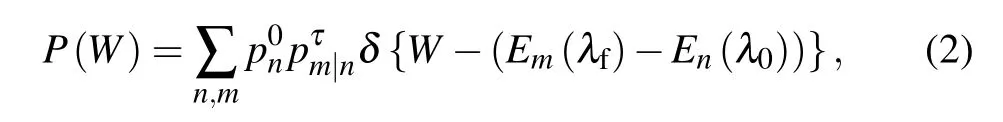
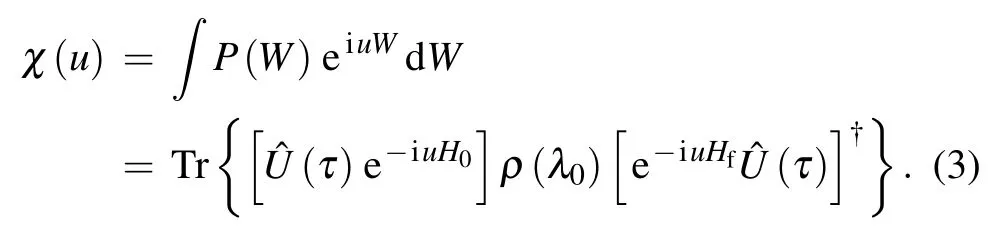
The Fourier transformation of the work distribution(2)is[10]Hereχ(u)is called the characteristic function.In the case of a sudden quenchˆU(τ)=1,[10]soχ(u)can be simplified to

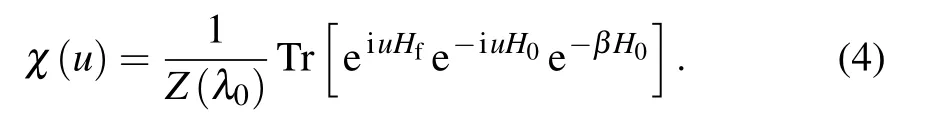
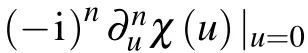
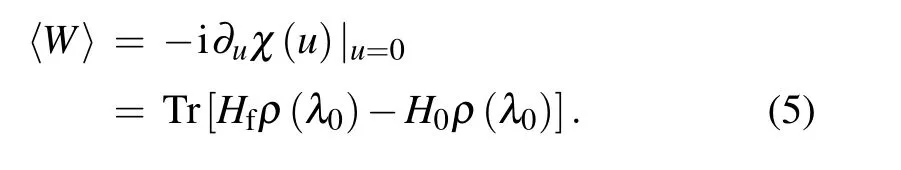
Consequently,the variance of the work distribution can also be obtained as

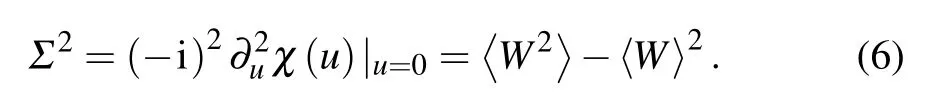
In order to know more about the nonequilibrium process,we also introduce the relative entropy to describe the distinction between the pre-quenched and post-quenched states[23–25]

where the relative entropy between density matricesρandκ is defined as

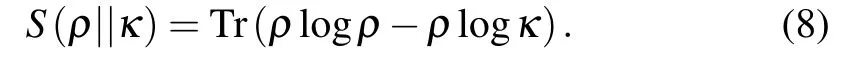
From Eq.(8),one knows that the relative entropy S(ρ||κ)≥0.The magnitude of S(ρ||κ)increases with the difference betweenρandκ.It has been proved that in the sudden quenching process,the relative entropy can be obtained as[23,24,26]

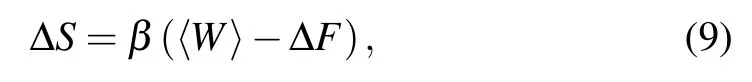
whereΔF=β−1ln[Z(λf)/Z(λ0)]is the free energy difference between the post-quenched and the pre-quenched states.

3.The XY spin chain with multi-spin interaction

The model under consideration is a spin-1/2 chain,in which both the nearest-neighbor spin interaction and the threespin interaction are included.Meanwhile,a transverse magnetic field is homogeneously applied to each spin of the chain.At time t=0,the Hamiltonian of this system is

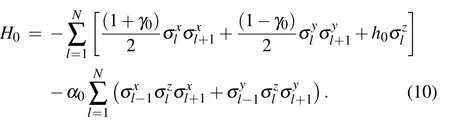
The Hamiltonian(10)can be fully diagonalized after carrying out the Jordan–Wigner transformation,the Fourier transformation and the Bogoliubov transformation.[49]We firstly introduce the Jordan–Wigner transformation

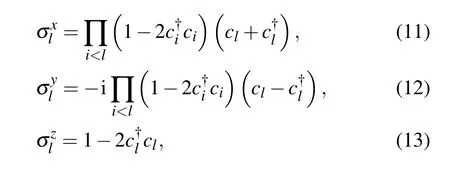
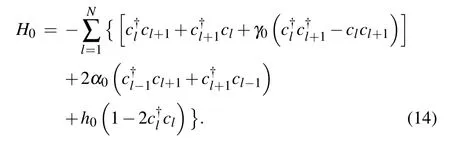
Based on Eqs.(14),we apply the Fourier transformation[49]

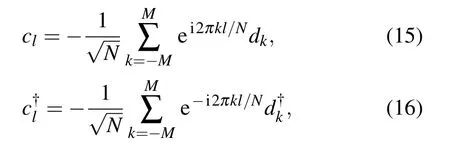
with M=N/2 for N even and M=(N−1)/2 for N odd.

From Eqs.(14)–(16),one gets

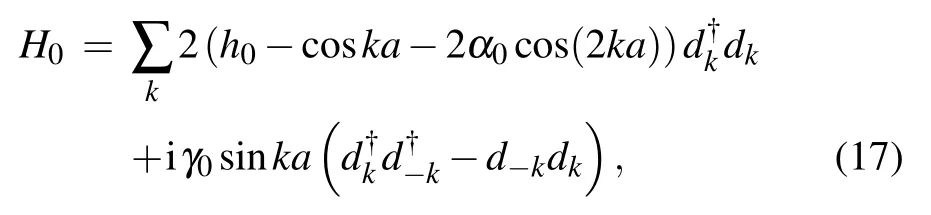
In order to fully diagonalize the Hamiltonian(17),we introduce the Bogoliubov transformation[49]

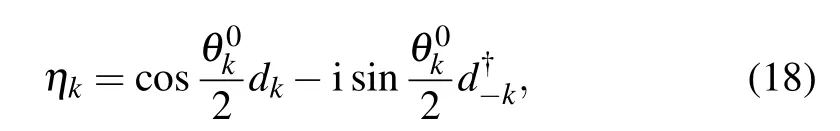
By substituting Eq.(18)into Eq.(17),the Hamiltonian(10)can be fully diagonalized as

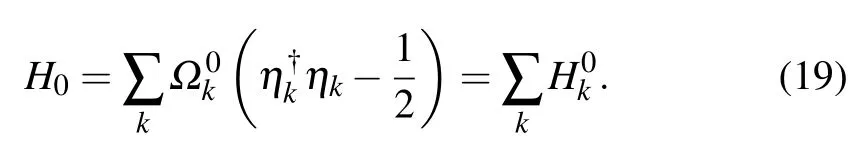
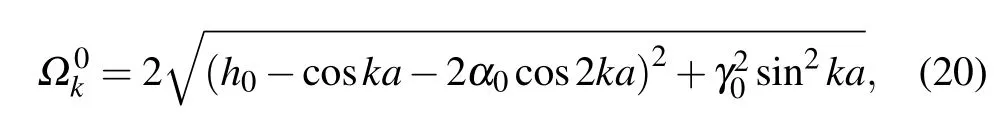
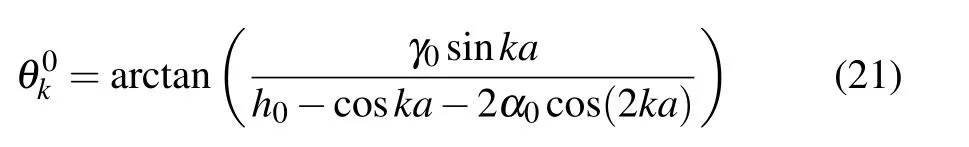
with a=2π/N.

After carrying out the sudden quenching operation,the system Hamiltonian changes to Hf.Using a similar diagonalization procedure outlined above,the quenched Hamiltonian can also be fully diagonalized as

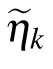
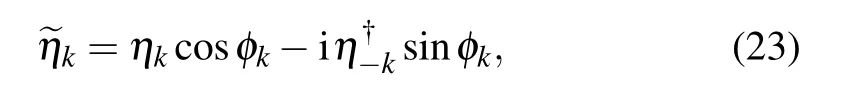
According to Eqs.(3)and(26),the characteristic function can be obtained as follows:

with

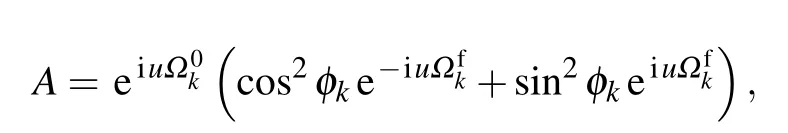
where A∗is the conjugate of A.From Eq.(28),both the Tasaki–Crooks and the Jarzynski relations can be verified.[5–8]Combining Eqs.(5)and(28),we obtain the analytical expression of the averaged work as follows:

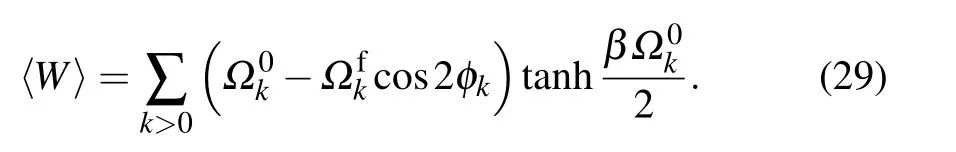
Furthermore,the fluctuation of the work distribution can also be obtained as follows:

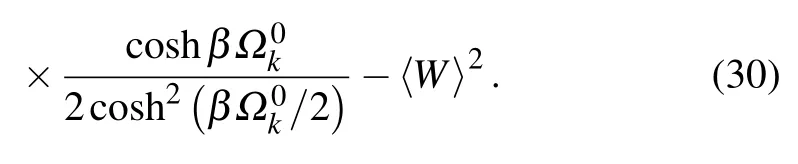
In addition,from Eqs.(9)and(29),the expression of the relative entropy can also be obtained as

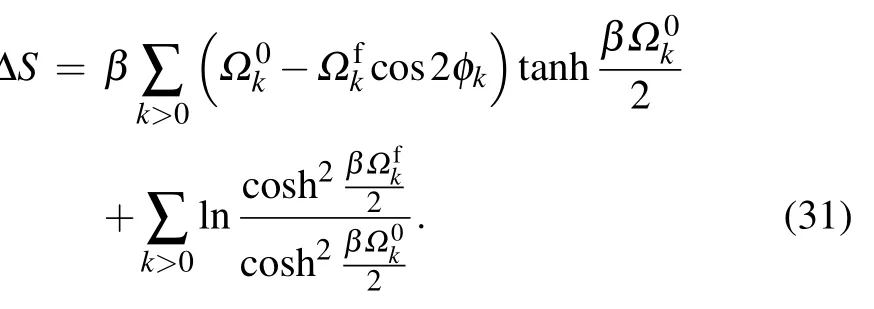
We here note that the expressions for the average work(29)and the relative entropy(31)are identical in form to the corresponding equations obtained in the Ising[2]and the XY models.[35]The difference comes from the dispersion relation and the Bogoliubov angle under different quenching conditions.Based on Eqs.(29)and(31),we will investigate the behavior of the average work and the relative entropy in the following section.

4.Results and discussion

In this section,we investigate the behavior of average work and relative entropy under different quenching conditions.There are three parameters in this system,i.e.,the anisotropic parameterγ0,the external field h0and the multispin interactionα0.Sinceγ0can not change the critical behavior of the XY model,we will concentrate on the behavior of the average work in the following two cases:(a)γ0and α0are fixed,h0is the quenching parameter,(b)γ0and h0are fixed,α0is the quenching parameter.

From Eq.(29),the averaged work under external field h0quenching is

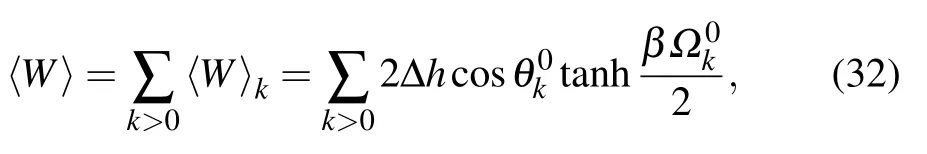
withΔh=h0−hf.

Similarly,the averaged work under multi-spin interaction α0quenching can be expressed as

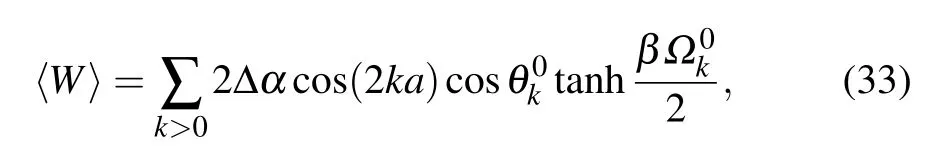
withΔα=αf−α0.

From Eqs.(32)and(33),we can see that〈W〉is proportional toΔλ=|λf−λ0|,withλ=h,α.Thus the〈W〉will be mainly decided by the system initial Hamiltonian.Based on Eqs.(32)and(33),the behavior of〈W〉under sudden quenching can be investigated.

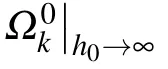
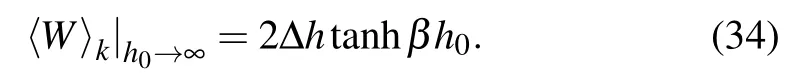
In combination with Eq.(32),we can know that〈W〉approaches NΔh in the h0→∞limit.This result is consistent with the asymptotic behavior that appears in the figures.In addition,〈W〉exhibits sudden change behavior during the evolution.The sudden change appears in the vicinity of the system’s QPT points which will be further proved in Fig.2.Moreover,Fig.1 also shows that the change ofγ0has no influence on the position of sudden change point,which further proves thatγ0does not change the QPT point of the system.[49,50]

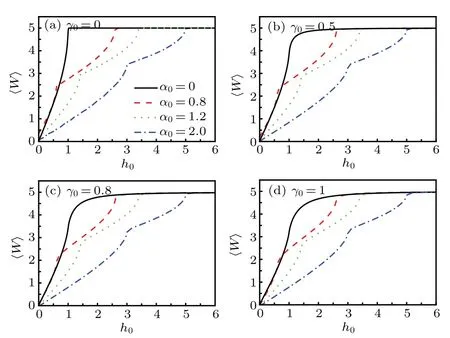
Fig.1.The average work as a function of h0 under variousα0 for Δh=0.01,with(a)γ0=0,(b)γ0=0.5,(c)γ0=0.8,and(d)γ0=1.The other parameters are chosen as N=500,β=100.The symbols shown in the subset of Fig.1(a)are applicable to all the curves.

In order to see more clear about the relations between〈W〉and the QPT,we investigate the evolution behavior of∂〈W〉/∂h0.From Eqs.(29)and(31),we obtain the first derivation of〈W〉to h0,

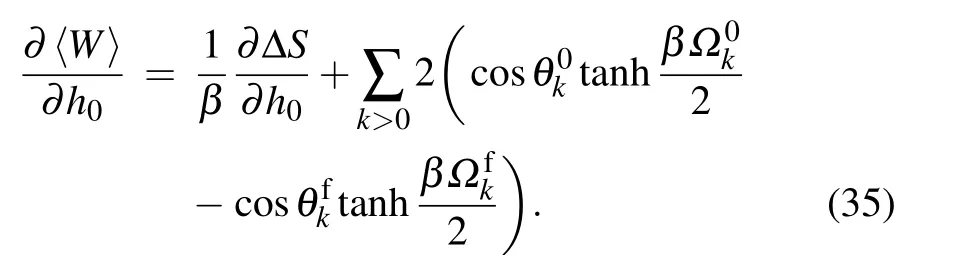
From Eq.(35),we infer that the evolution of∂〈W〉/∂h0and ΔS may have some similarities.

Based on Eq.(35),one can investigate the evolution of∂〈W〉/∂h0with h0,as shown in Fig.2.The plotting parameters are the same as those in Fig.1.It is seen from Fig.2 that whenα0=0,∂〈W〉/∂h0displays peaks at h0=1 for arbitraryγ0.When the three-spin interaction is switched on(α0/=0),the peaks have 2α0displacement from h0=1.This result corresponds exactly to the critical line determined by h0±1−2α0=0.[48]Moreover,one also knows that the peak positions in Fig.2 are identical with those of the sudden change points in Fig.1.Combining Figs.1 and 2,we infer that〈W〉can be used as a detector of QPTs and multi-spin interaction at finite temperature in the non-equilibrium system.

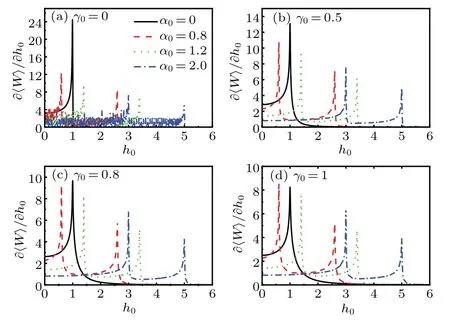
Fig.2.The first derivation of average work as a function of h0 under variousα0 forΔh=0.01.The plotting parameters are the same as those of Fig.1.The symbols shown in the subset of Fig.2(a)are applicable to all the curves.

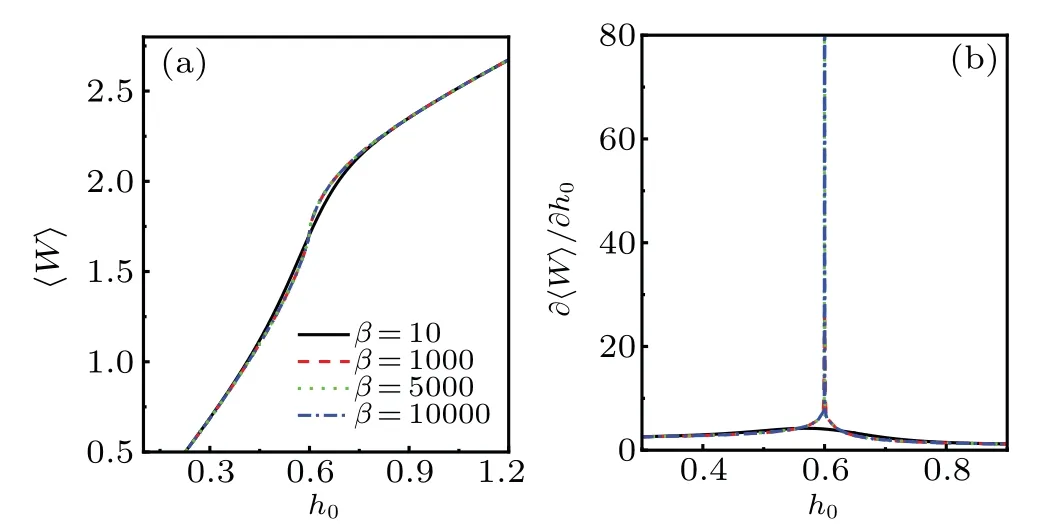
Fig.3.The average work〈W〉and its first derivation∂〈W〉/∂h0 as a function of h0 under variousβ.The other parameters are chosen as(a)γ0=1,α0=0.8,and N=500.The symbols shown in the subset of Fig.3(a)are applicable to all the curves.

In Fig.3,the influences of temperatureβon the evolution of〈W〉and∂〈W〉/∂h0are investigated.The other parameters are chosen asγ0=1,α0=0.8,and N=500.It shows thatβ hardly affects the evolution of〈W〉and∂〈W〉/∂h0except in the vicinity of critical points.At the critical points,the peaks of∂〈W〉/∂h0are sensitive to the decreasingβ.This proves that the QPTs phenomenon is sensitive to the thermal fluctuation.In fact,the critical behavior of∂〈W〉/∂h0can be predicted by Eq.(32)in the large N limit.From Eq.(32)we can obtain

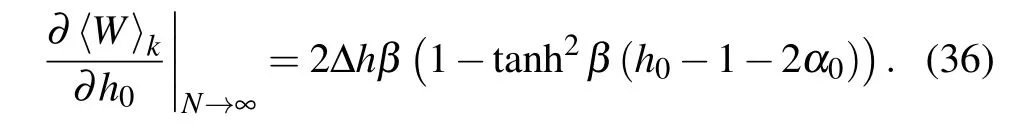
Equation(36)indicates that∂〈W〉k/∂h0will exhibit a peak if h0−1−2α0=0.This result is consistent with the peaks appearing in Figs.2 and 3(b).

In Fig.4,〈W〉as a function ofα0under variousγ0for Δα=0.01,with h0=0,0.5,1 and 3 are given.The other parameters are chosen as N=500,β=100.It shows that〈W〉decreases with the increasingα0for fixedγ0and h0.There exists sudden change phenomenon during the evolution.The sudden change point has h0/2 displacement fromα0=0.5.Theγ0just influences the magnitude of〈W〉rather than the sudden change point position.From Eq.(32)we know that the influences ofγ0on〈W〉will be suppressed for large h0andα0,which leads to the near superposition of the curves in Fig.4(d).

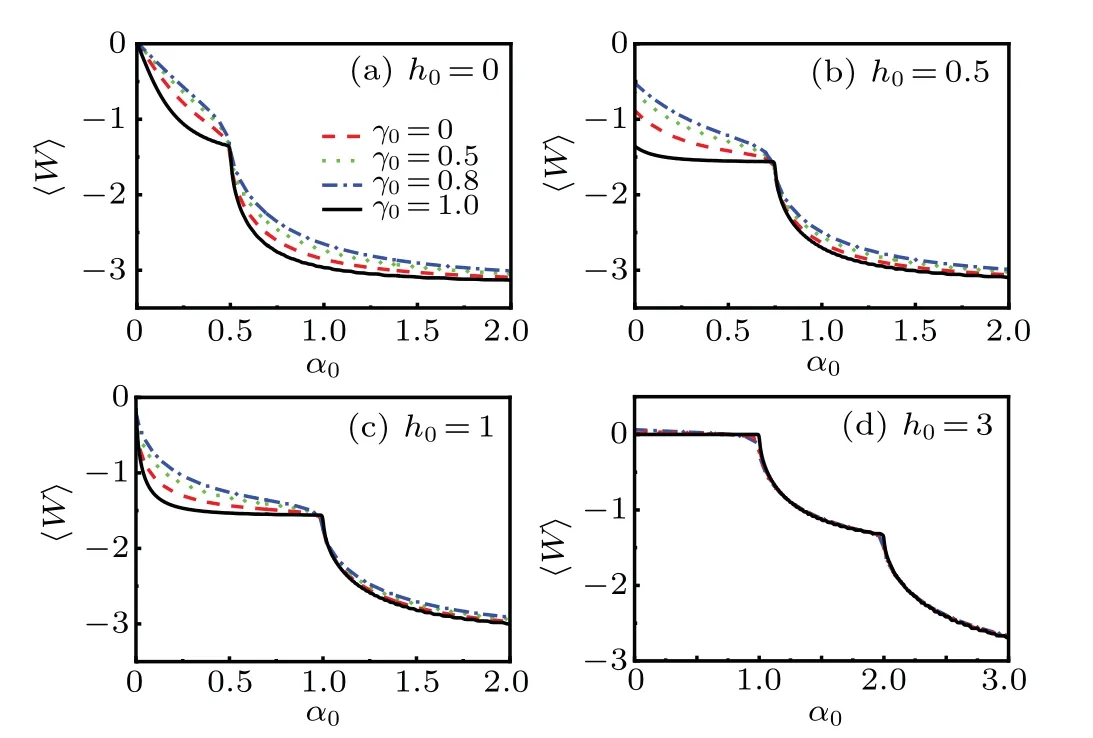
Fig.4.The average work as a function ofα0 under variousγ0 for Δα=0.01,with(a)h0=0,(b)h0=0.5,(c)h0=1,and(d)h0=3.The other parameters are chosen as N=500,β=100.The symbols shown in(a)are applicable to all the curves.

The relations between the pre-and post-quenched states can be revealed through the investigation of the relative entropy.From Eqs.(9)and(28),the expressions of relative entropy under different quenching parameters can be obtained.From Eq.(9),the relative entropy under h0quenching can be expressed as

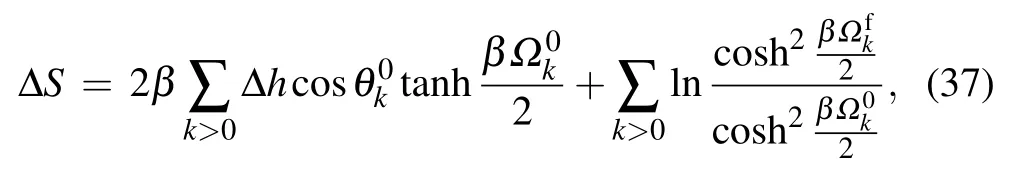
The relative entropy under external fieldα0quenching is

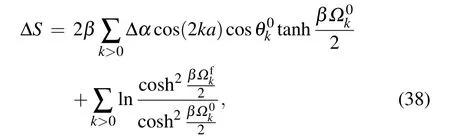
Figure 5 plots the relative entropyΔS as a function of h0under variousα0forΔh=0.01,withγ0=0,0.5,0.8 and 1.Other parameters are chosen as N=500 andβ=100.It shows thatΔS displays a peak at h0=1 whenα0=0.The peak has a 2α0displacement from h0=1 whenα0/=0.This result is similar to that of∂〈W〉/∂h0in Fig.2 and is consistent with the critical line h0±1−2α0=0 in Ref.[48].SinceΔS describes the entropy distance between the initial equilibrium state and the final quenched one.The sharp peaks indicate that a small change of external field will lead to a dramatic change in the equilibrium state near the critical points.[34,37]Further,the multi-spin interaction suppressesΔS and leads to the decreasing of the peaks.Based on Fig.5,we say thatΔS can also be used as the detector of QPT and the three-spin interaction.

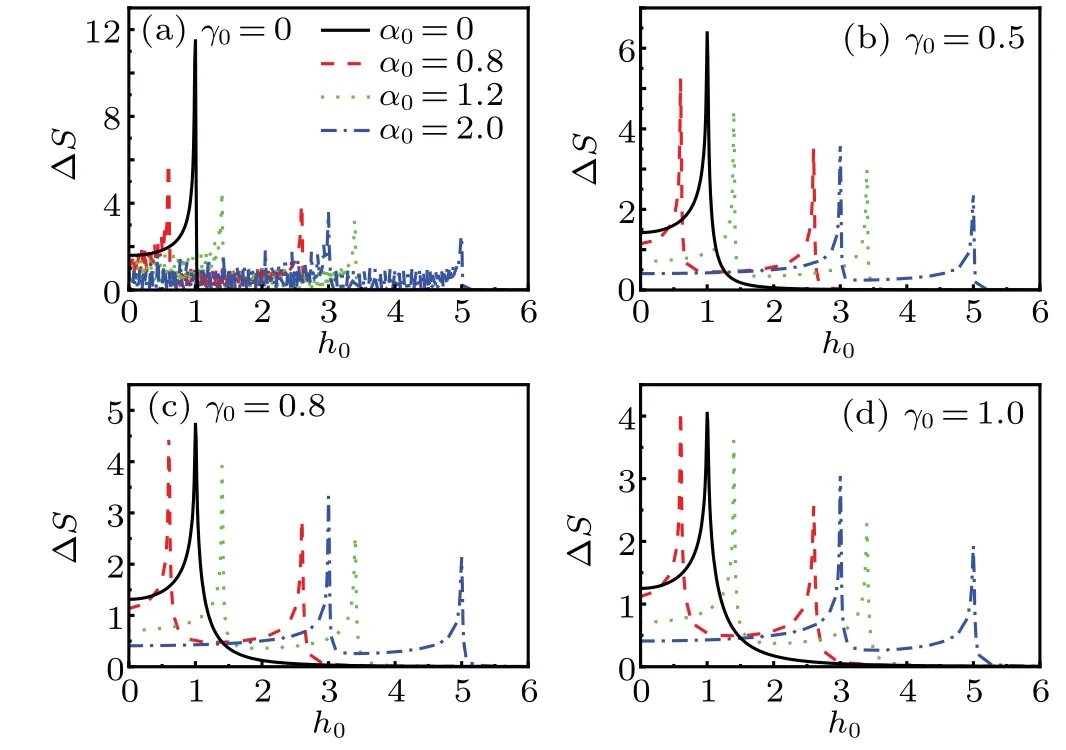
Fig.5.The relative entropy as a function of h0 under variousα0 for Δh=0.01,with(a)γ0=0,(b)γ0=0.5,(c)γ0=0.8,and(d)γ0=1.The other parameters are chosen as N=500,β=100.The symbols shown(a)are applicable to all the curves.

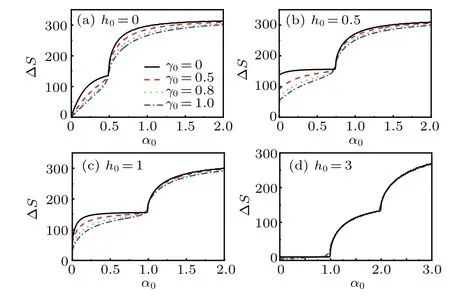
Fig.6.The relative entropy as a function ofα0 under variousγ0 for Δα=0.01,with(a)h0=0,(b)h0=0.5,(c)h0=1,and(d)h0=3.The other parameters are chosen as N=500,β=100.The symbols shown in(a)are applicable to all the curves.

In Fig.6,ΔS as a function ofα0under variousγ0for Δα=0.01 with h0=0,0.5,1 and 3 are given.Other parameters are chosen as N=500,β=100.We can see thatΔS increases with the increasingα0and saturates to constant values.There also exists sudden change behavior during the evolution.For h0=0,the sudden change point locates atα0=0.5 as shown in Fig.6(a).For h0/=0,h0andα0jointly influence the phase transition process and lead to the displacement of sudden change point.

In Fig.7,the influences ofβon the evolution ofΔS with h0andα0are investigated.The other parameters are chosen as N=500,(a)γ0=1,α0=0.8 and(b)γ0=0.8,h0=1.It shows thatΔS exhibits peaks(sudden change behavior)during the evolution with h0(α0).The peak values decrease with the decreasingβ.This indicates that at high temperature the thermal fluctuation dominates the quantum one,which leads to the elimination of the QPT phenomenon.

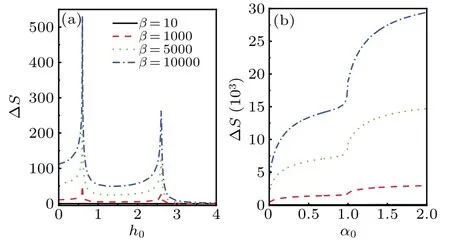
Fig.7.The relative entropy as a function of(a)h0 and(b)α0 under variousβ.The other parameters are chosen as(a)γ0=1,α0=0.8;(b)γ0=0.8,h0=1,and N=500.The symbols shown in(a)are applicable to all the curves.

5.Summary

In summary,we have studied the non-equilibrium thermodynamics of a quenched XY spin chain with multi-spin interaction in a transverse field.The spin chain is driven out of equilibrium through sudden quenching.The analytical expression of the average work〈W〉and the relative entropyΔS are obtained under different quenching conditions.The influence of the external field h0,the multi-spin interactionα0and the temperatureβon the properties of the〈W〉,the first derivation of〈W〉and theΔS are investigated.Our results show that at finite temperature they exhibit sudden change or sharp peaks during the evolution with the quenching parameters.The locations of sudden change and the sharp peaks correspond to those of the quantum phase transition(QPT)points.In addition,our results show that the positions of sudden change and peaks are obviously shifted away from the original ones(h0=1).The magnitude of multi-spin interaction dominates the displacement of the sudden change and the peaks.Based on these results we infer that the average work and the relative entropy can be used as a detector of QPT points and the multi-spin interaction in the non-equilibrium system.

As a comment,by comparing the sudden change(peak)locations of the average work(the relative entropy)with the critical points which are identified by pairwise quantum discord and classical correlation in Ref.[48],we find that the sudden change(peak)locations of the average work(the relative entropy)are around the critical points.In previous investigations,[48,50–53]it has been shown that quantum discord,entanglement and fidelity or their derivatives with respect to parameters in the Hamiltonian display the singular behavior at critical points and can be used to detect QPTs.Therefore,we believe that these parameters can also be used to detect three-spin interaction in nonequilibrium systems.