含飞轮储能微网的新型频率控制

颜玉玲，梅容芳，黄余，黄白涛

（1.宜宾职业技术学院电气信息系，四川宜宾，644004；2.新能源电力系统国家重点实验室（华北电力大学），北京 102206）

目前，储能系统已广泛应用于微电网中。微电网中最重要的储能系统有电池储能系统（battery energy storage system，BESS）、超级电容（super capacitor，SC）和飞轮储能（flywheel energy storage system，FESS）[1]。BESS可以存储和提供大量的能量，但由于内部的化学过程，其斜坡率受到限制[2]。SC也可以存储和提供大量的电能，但其储能容量较低。FESS的斜坡率大于BESS[3]而小于SC，而储能容量大于SC而小于BESS。此外，与BESS不同，FESS的寿命很长，因此完全适用于微电网的频率变化补偿[4]。近年来，大规模无轴设计的FESS大大提高了FESS的容量。如文献[5]中提出了一种低速无轴无轮毂大规模FESS，其能量和功率分别为100 kW·h和100 kW。此外，基于永磁同步电机（permanent magnet synchronous motor，PMSM）的高速FESS设计也引起了众多研究者的关注。

目前，许多研究工作都集中在FESS的应用上，其中大部分是用于实现风力涡轮机和光伏（photovoltaic，PV）等可再生资源的输出功率平滑[6]。FESS可以补偿它们的输出功率波动。文献[7]引入了飞轮储能矩阵系统来平滑风电场输出功率。该协调控制策略的目标是多个FESS单元的协同控制，以产生一个参考功率值。PMSM和感应式电机（induction motor，IM）是FESS中常用的电机。此外，其他一些研究人员也将开关磁阻电机（switched-reluctance motor，SRM）归为常用类型电机[8]。基于IM的FESS是一种低成本的解决方案，但其控制系统比基于PMSM的控制系统复杂。文献[9-10]分别提出了基于IM的FESS风力平滑的磁场定向控制（field-oriented control，FOC）和直接转矩控制（direct torque control，DTC）方法。文献[11]提出了基于小波模糊神经网络的风力发电机扰动平滑控制方法。同样，文献[12]在FESS结构中采用了绕线转子IM，该结构具有人工神经网络控制器。虽然在双馈馈电系统中，变流器的额定功率降低了，但损耗却增加了。文献[13]集成了基于IM的FESS和基于DFIG的风力发电机，通过基于最优能量函数的控制策略，最大限度地传递风力发电的能量，并增强其低压通过特性。此外，许多学者研究了FESS在电力系统和微电网调频的应用。如在文献[14]提出了一种模糊PD控制器，用于风力发电机组的频率调节。模糊规则表的设计是该方法的一个挑战。在M端变流器中实现了频率控制器。同时，也没有从启动模式到补偿模式转换的协调系统。文献[15]提出了一种用于频率调节的混合FESSBESS结构。功率分配由中央控制器处理，所需功率的高频部分分配给FESS。该系统需要对测量的功率进行数据传输。同时，FESS的控制方法也是基于传统的FOC。文献[16]提出了一种用于含同步发电机和风力机组的微电网的频率调节方法。传统方法中，频率是由G侧变流器测量，但用于M侧变流器的控制回路。测量频率的传递可能面临噪声。另一方面。由于M端变流器的频率控制回路必须先向直流端口注入功率，所以频率控制是间接进行的。然后G侧变流器必须将同样的注入功率传输到电网以固定直流端口电压。因此，它可能会导致补偿延迟和更多的频率偏差。

从实际角度来看，另一个值得注意的问题是FESS控制系统中启动和补偿模式之间的协调[17]。当FESS连接到微电网时，它必须在充电模式下启动，以达到额定速度。然后，模式转变为补偿模式，以调节频率。控制系统模式的不协调，可能导致系统不稳定。基于此，本文提出了一种用于微电网频率调节的新型FESS控制方法，以减小频率偏差和直流端口电压的波动。该方法支持低电压变化下的启动、补偿模式和模式转换。与传统控制方法比较，该方法在G侧变流器中引入了频率控制器，以提高FESS斜坡率，减小频率随负载变化的偏差，而M侧变流器的三层控制系统则减小了直流端口电压的波动[18-19]。

1 控制系统设计

1.1 孤岛微电网的典型结构

图1为含飞轮储能微网的典型结构图。

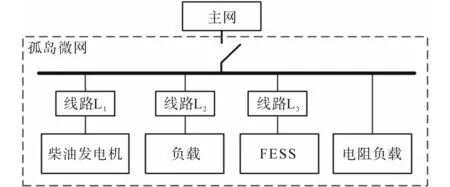
图1 含飞轮储能微网的典型结构图Fig.1 Structure of the typical microgrid with FESS

如图1所示，该微电网由发电单元、负载、储能系统和电阻负载组成。图2为FESS的拓扑结构。

从图2可以看出，FESS的直流端口电压取决于PC：

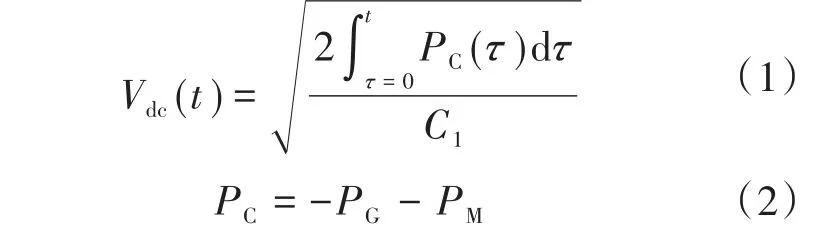
在传统的FESS调频控制方法中，当微网频率降低时，M侧变流器将所需的功率从IM转移到直流端口。G侧变流器将相同的功率从直流端口转移到微电网，以调节直流端口的电压。FESS的传统控制系统如图3所示[20]。

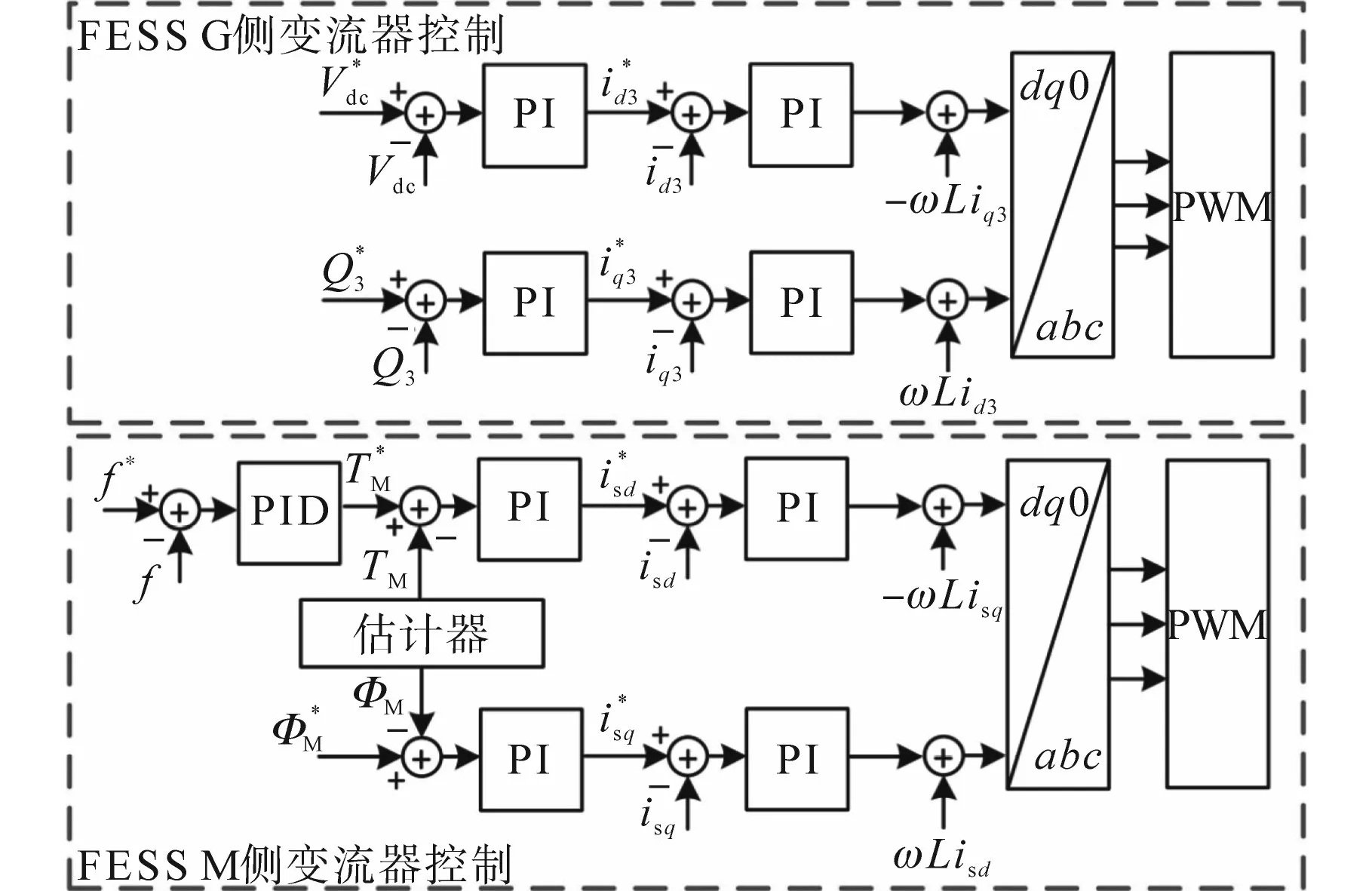
图3 FESS G侧和M侧变流器的经典控制系统Fig.3 Conventional control system for G-side and M-side converters of FESS

图3中，ω为飞轮转速的测量值；TM为电磁转矩；ΦM为感应电机磁通；Q3为FESS G侧变流器的输出无功功率；f为微网的频率；L为滤波器的电感；id为d轴的输出电流；iq为q轴的输出电流。在M侧变流器控制系统中，PID控制器通过微网实测频率与额定值的比较，生成IM的参考TM。将TM的基准输入到传统的FOC系统中驱动IM。此外，G侧变流器的目的是调节直流端口电压和控制向电网注入无功功率。

1.2 本文所提控制法

图4为本文所提控制方法的方框图。

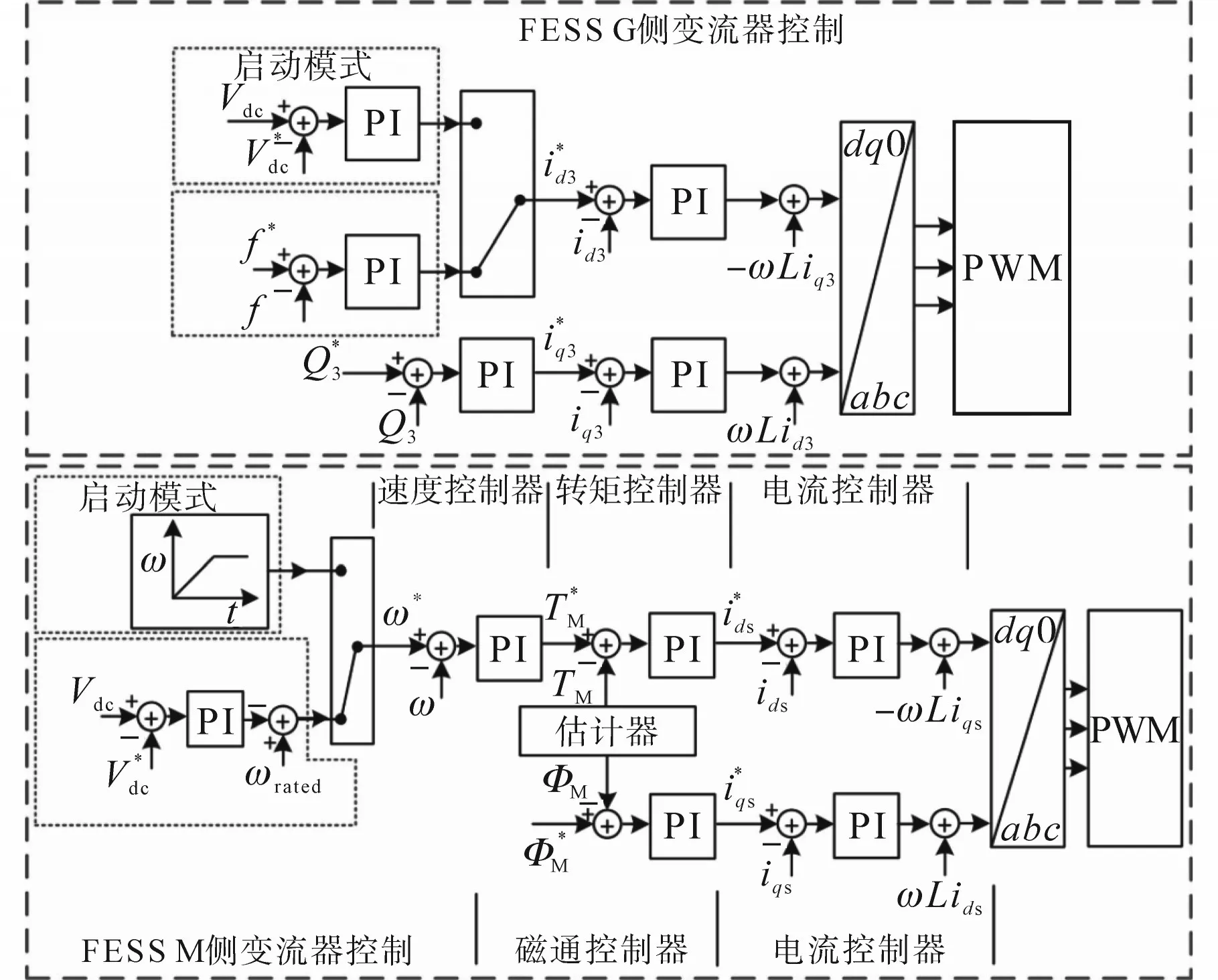
图4 FESS G侧和M侧变流器的所提控制系统Fig.4 Proposed control system for G-side and M-side converters of FESS

在该控制系统中，FESS具有两种模式：启动模式和补偿模式。启动模式下，M侧变流器给飞轮充电，使其达到额定转速。当FESS连接到微网时，运行在启动模式，因此，根据图4，M侧变流器通过速度控制器来控制飞轮转速，参考速度先是上升，然后是恒定速度，在这种模式下，M侧变流器从直流端口吸收飞轮所需的功率，G侧变流器从微电网吸收所需的电力，用于直流端口电压调节。在启动模式结束时，FESS达到额定转速，其由启动模式变为补偿模式。

与传统控制系统不同，本文提出控制系统的补偿模式，G侧变流器通过吸收或注入来自微电网的功率来调整微电网的频率，而M侧变流器通过吸收或注入飞轮需要的功率来控制直流端口电压。如图4所示，在所提出的G侧变流器控制系统中，i*d3在启动模式下由直流端口电压调节器产生，补偿模式下由频率调节器产生。为了避免模式转换时的摆动，直流电压调节器和频率调节器的输出必须相等。从图4可得，M侧变流器在d轴上采用了4个级联控制层。在FOC方法的基础上，在d轴和q轴上采用了两个基于PI电流控制器来产生脉宽调制（pulse width modulation，PWM）单元的参考电压。参考电流（i*ds和i*q3）分别由基于PI转矩控制器和磁通控制器产生。与传统的控制系统不同的是，采用基于PI速度控制器来产生转矩控制层的参考转矩。在启动模式下，速度控制器的参考速度为一个斜坡（从零到额定速度）。但是在频率补偿模式下，参考转速等于额定转速减去直流电压控制器的输出。在从启动模式到补偿模式的过渡过程中，该方法大大减小了直流端口电压的振荡。在过渡时刻，基于PI直流端口电压控制器的输出为零；因此，过渡前后ω*的值等于额定转速。

当突变负载影响微电网时，由于柴油发电机调速器系统的低速响应，频率降低。因此，由图4可知，FESS的G侧变流器的频率控制器增加i*d3，向微电网注入所需的失配功率。与传统频率控制系统位于M侧变流器控制系统（见图3）不同，本文控制系统中频率控制器位于G侧控制系统。它具有更快的功率注入或吸收，有效减少微电网的频率偏差，所需的功率由直流端口电容提供，然后由M侧变流器的直流端口电压控制器从IM向直流端口注入相同的功率来调节直流端口电压。为了克服由此产生的直流端口电压波动，本文在M侧变流器控制系统中引入了级联直流端口电压控制器和速度控制器，如图4所示。因此，该控制系统的优点是频率偏差小，直流端口电压变化小。G侧变流器的开关脉冲由PWM单元产生，由两个电流控制器d轴和q轴供电。d轴电流控制器的参考电流由PI控制器产生，在补偿模式下调节微网频率，在启动模式下控制直流母线电压。q轴电流控制器的参考电流由PI控制器产生，控制微电网的无功注入。

2 系统稳定性分析与参数选择

2.1 孤岛微电网的线性化模型

本节研究上述微电网的线性化模型，以确定稳定微电网的PI系数，并对线性化模型和工作点附近的小信号分析进行比较。G侧变流器及其控制系统如图5所示。直流连接电压（Vdc）不是恒定的。

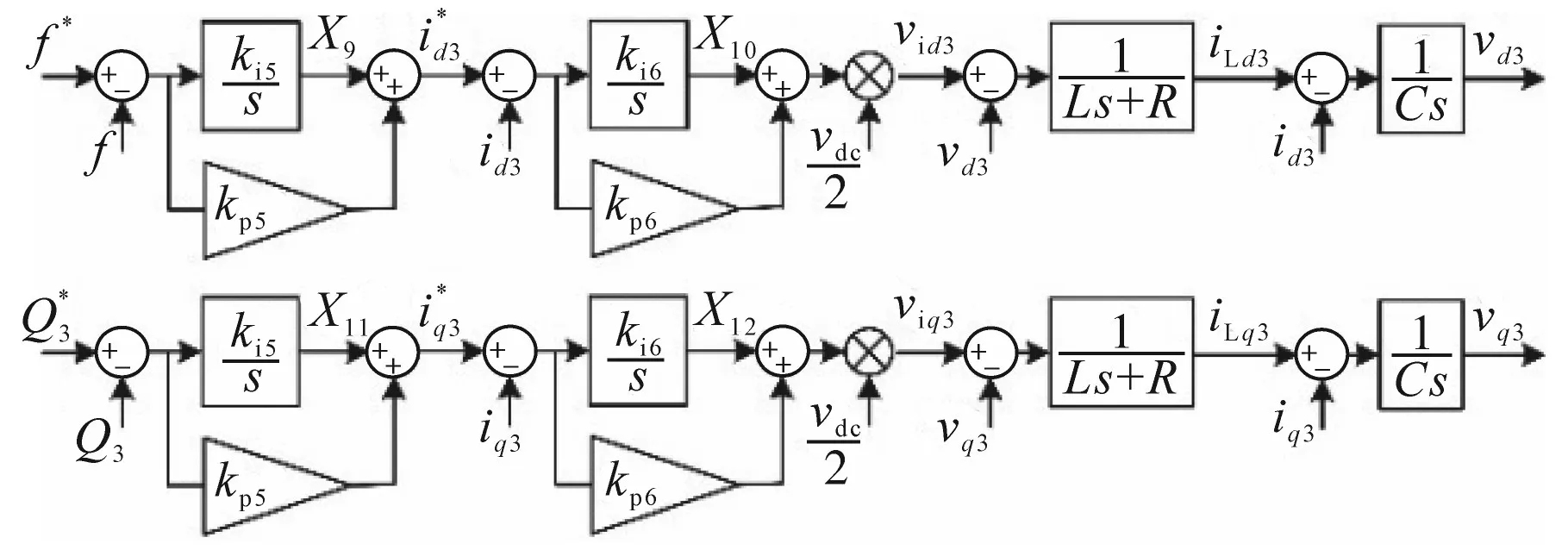
图5 G侧变流器及其控制系统Fig.5 G-side converter and its proposed control system

依据图5中变量X9，X10，X11，X12，则d轴方程为

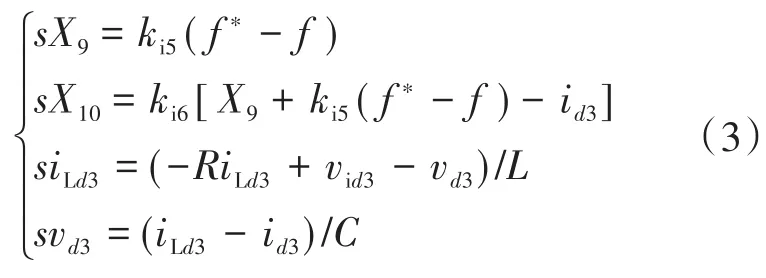
根据泰勒展开式，可得：

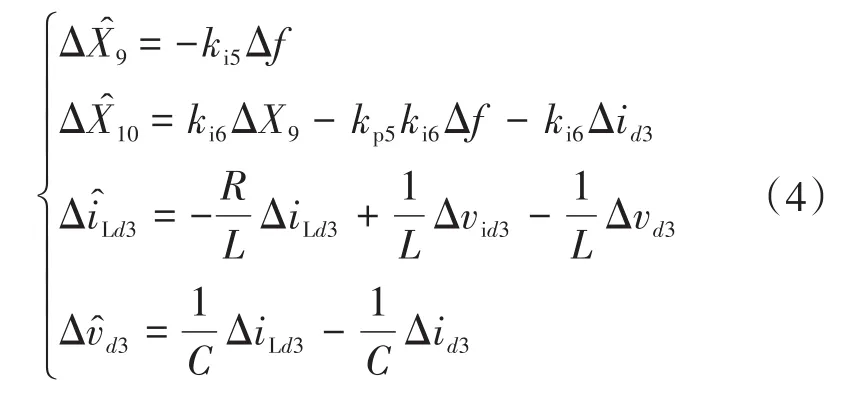
式中：C为滤波器电容。

q轴方程可以写成类似的形式。故G侧逆变器（ΔXGS）的状态空间变量向量由下式表示：

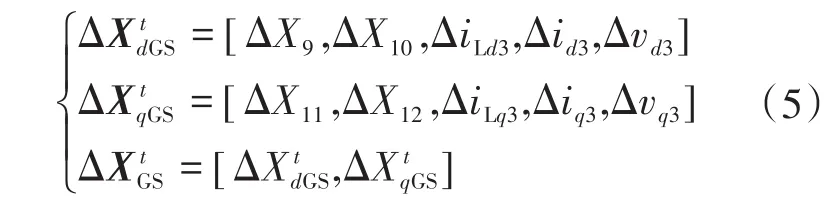
M侧变流器及其拟控制系统和线性化的IM模型如图6所示。

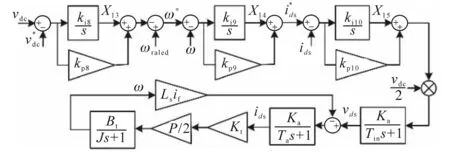
图6 M侧变流器及其控制系统和线性化的IM模型Fig.6 M-side converter，its proposed control system and linearized IM model

图6中有变量X13，X14，X15，则d轴方程为

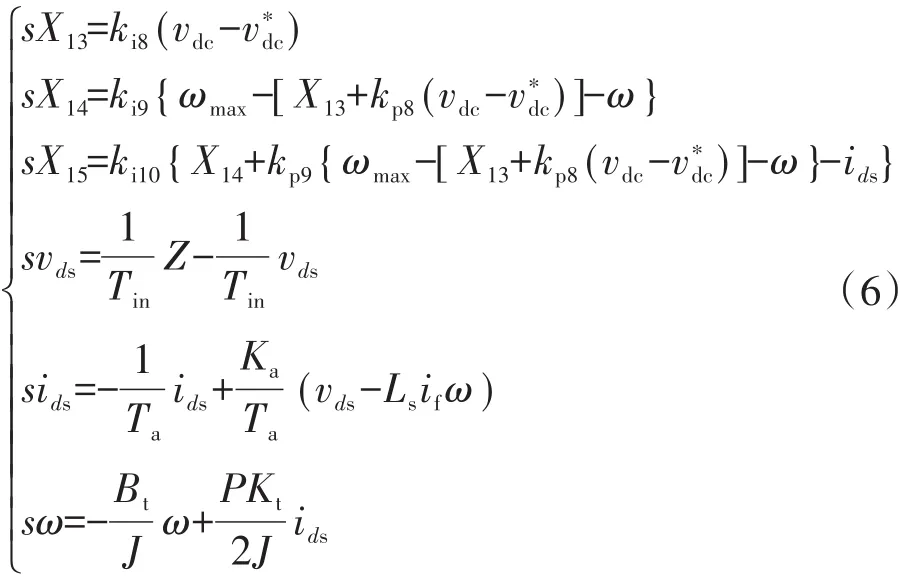
据泰勒展开式，可得：

q轴方程可以写成类似的形式。故G侧逆变器（XMS）的状态空间变量向量为

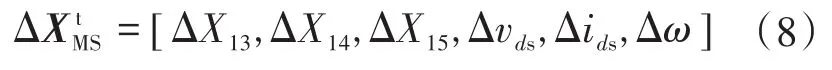
各模块的输出电流可按如下方式确定：

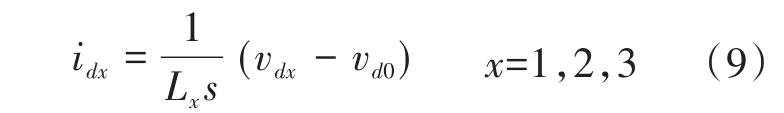
其中

得到：

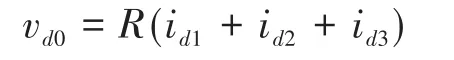
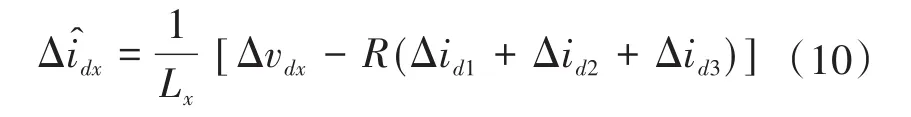
假定v2dc=X16，则FESS直流端口电容方程可表示为

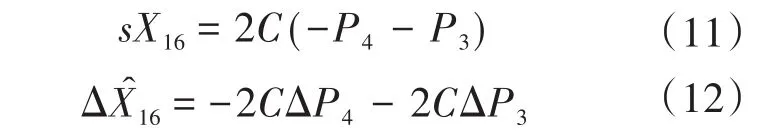
同样，由于v2dc=X16，可得：

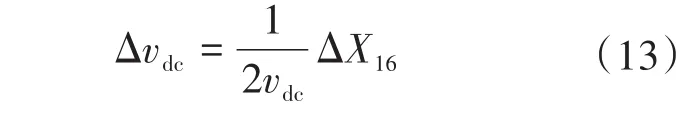
2.2 线性化微网控制系统设计与稳定性分析

考虑上述方程的状态变量向量，线性化后的微网状态变量方程为

因此，微电网的状态空间方程可以写成这种线性形式：

该线性化模型的参数设计和性能评价，可通过根轨迹图中状态矩阵A的特征值来确定。每个特征值可能与几个状态变量有关。利用灵敏度分析，可以确定不同状态变量在每个特征值中的参与程度。经典法与本文所提方法的根轨迹图如图7所示。

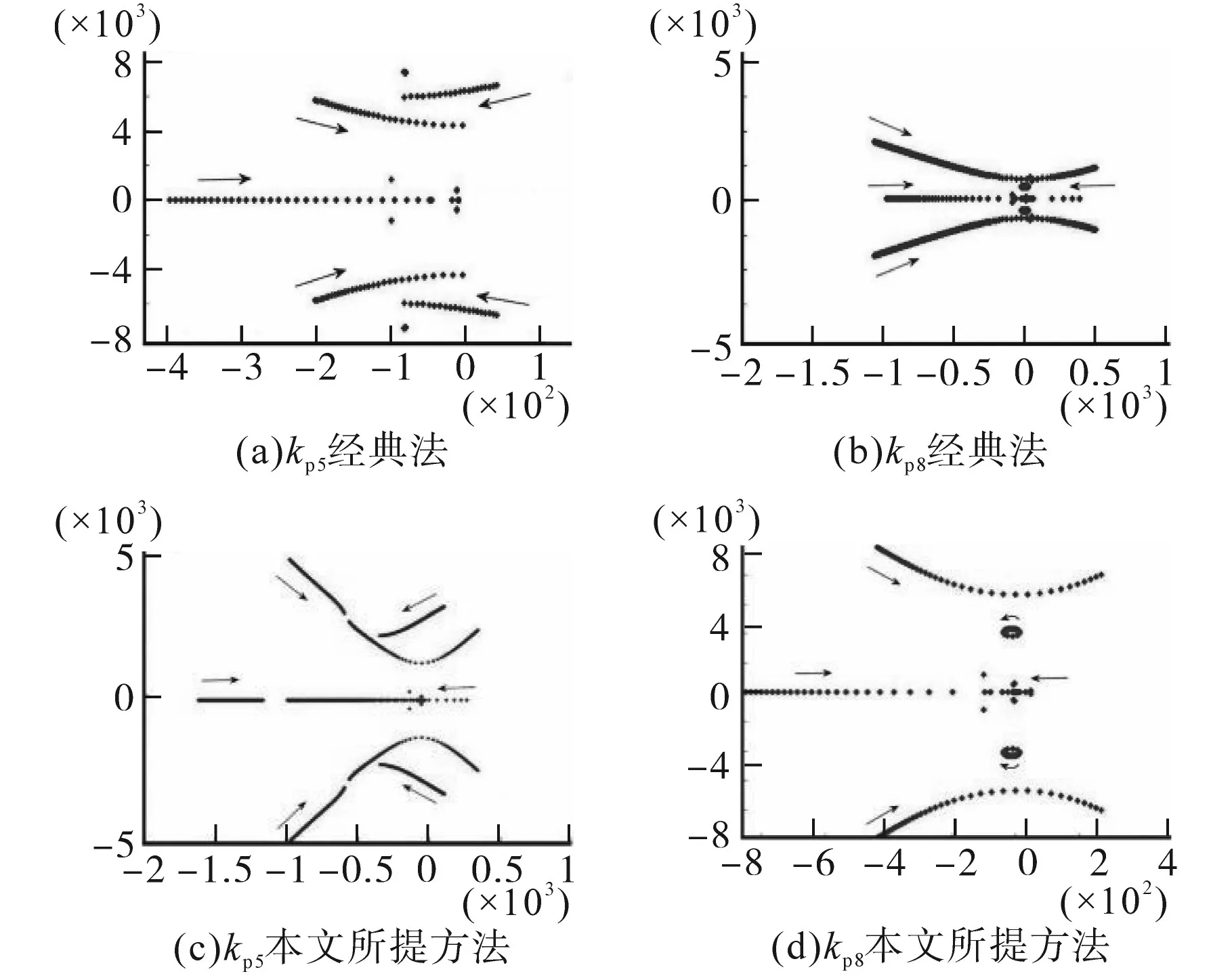
图7 经典方法和提出方法的根轨迹Fig.7 Root locus of the classical method and the proposed method

由图7可知，低频特征值主要与FESS的频率控制器或直流电压控制器等功率控制层参数有关。低频模态对系统稳定性的影响最大。图7c显示了根轨迹图中特征值随所提方法的频率控制器（kp5）比例增益的变化轨迹。当kp5从0.01增大到1时，两种低频模态均受到较大影响。其中一个会导致kp5＞0.65的系统不稳定。另一个会导致kp5＜0.11时系统不稳定。因此，为kp5找到了稳定裕度。为了在这个时间间隔内找到kp5的最优值，使用基于遗传算法的优化来达到最小的超调量和稳定时间。在图7d中，模式的轨迹可以看作是本文方法的直流端口电压控制器（kp5）的比例增益从0.01～1的函数。在这种情况下，模态的灵敏度变得更高。图7a和图7b为常规方法相同的结果。可以看出，传统方法的变化范围比本文方法大，因此本文方法的控制器系数的稳定范围更大。

3 实验验证

为验证本文所提方法的可行性与有效性，实验系统典型微电网的实验设置如图8所示。实验系统额定功率为3 kW，线路电压为有效值220 V。FESS、柴油发电机模拟器（DGE）和负载模拟器（LE）的参数分别出自文献[21-23]中。为了优化PI系数，首先用Matlab/Simulink软件对系统进行了仿真。然后，根据小信号模型和灵敏度分析，对PI系数进行了优化设计，限于篇幅，具体优化方法可见文献[24-25]。

图8 典型微电网的实验设置Fig.8 Experimental setup of the typical microgrid

3.1 负载变化场景

为了验证本文所提方法的有效性和优越性，本文给出了周期性三角形和阶跃负载变化在以下场景下的实验结果。

场景一：无FESS频率控制，将DGE，LE和电阻负载接入孤岛微电网。起初，负载功率为800 W，同时将负载模拟器的有功功率和无功功率置零。在t=45 s时，LE模拟1 600 W的步进负载变化。图9为DGE和LE的有功功率。在t=55 s，一个3 200 W的三角周期性负载接入，LE和DGE的有功功率如图10所示。

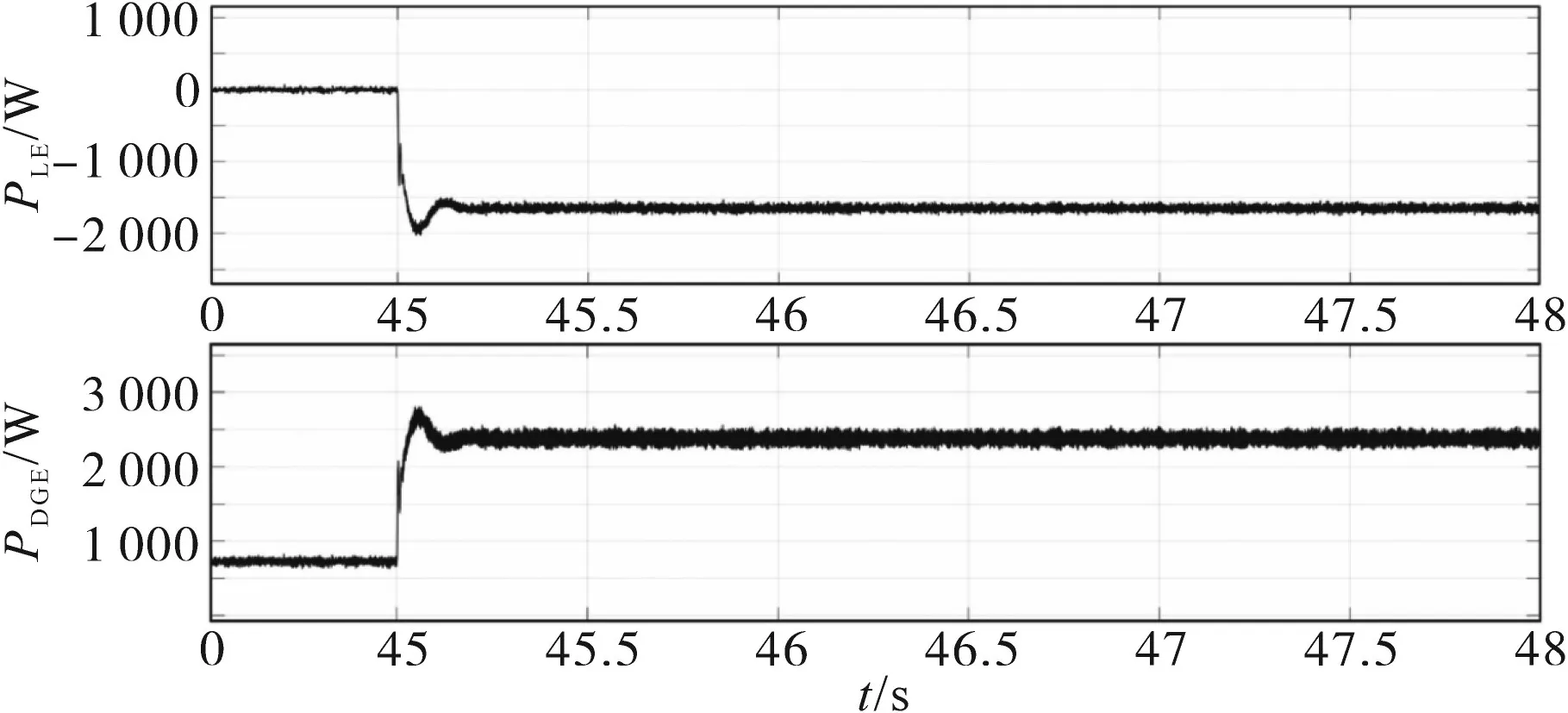
图9 场景1阶跃负载变化时LE和DGE的有功功率Fig.9 Active powers of LE and DGE for step load change in scenario 1

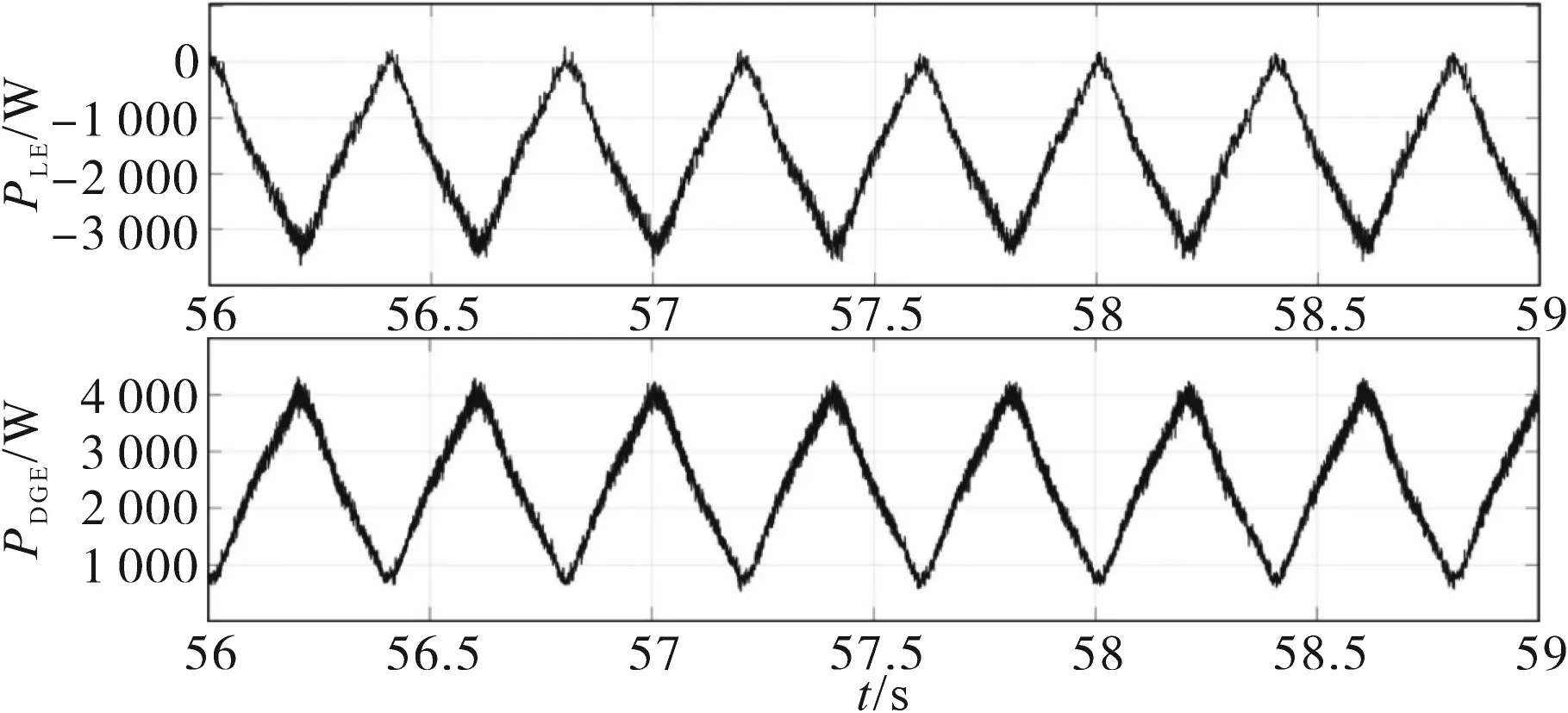
图10 场景1三角周期负载变化时LE和DGE的有功功率Fig.10 Active power of LE and DGE in scenario 1 with triangular cyclic load variation

场景二：采用经典方法。

场景三：采用本文所提方法。

在场景二和场景三中，分别使用经典和本文所提的控制方法将FESS增加到场景一的系统中。首先，电阻负载功率为800 W，将LE的有功、无功功率设置为零，FESS仅因空载损耗而吸收功率。在t=45 s时，LE模拟1 600 W的步进负载变化。

图11，图12分别为采用常规方法和本文所提方法的阶跃负载变化时FESS，LE，DGE的有功功率。

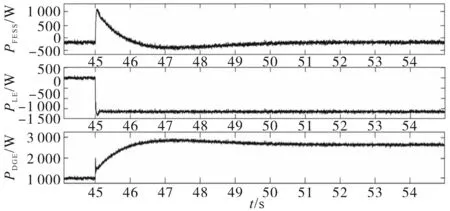
图11 阶跃负载变化时FESS，LE，DGE的有功功率（常规方法）Fig.11 Active powers of FESS，LE and DGE for step load change（conventional method）

图12 阶跃负载变化时FESS，LE，DGE的有功功率（本文所提方法）Fig.12 Active powers of FESS，LE and DGE for step load change（proposed control method）

从图11和图12中可以看出，FESS可快速注入所需的功率，并在两种方法中防止频率下降。然后，DGE功率缓慢增加，FESS重新充电。此外，可以看出，本文所提方法下FESS的功率注入比传统控制方法要快。

在t=45 s时，DGE注入功率突然减少，同时频率也下降。在t=55 s时，LE增加周期负载，采用经典法和本文所提法的FESS，LE及DGE有功功率如图13和图14所示。FESS提供了减少频率变化所需的主要功率。比较图13和图14可得，本文所提方法下FESS针对LE变化的响应速度更快，这为DGE能够缓慢增加功率提供了条件，这也更符合柴油发电机的输出特性。

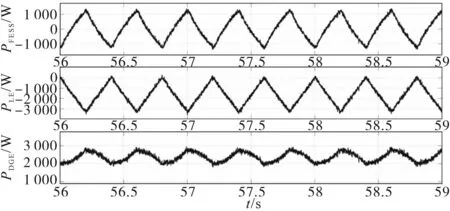
图13 三角周期负载的FESS，LE及DGE有功功率（经典法）Fig.13 Active powers of FESS，LE and DGE for triangular periodic load（conventional method）

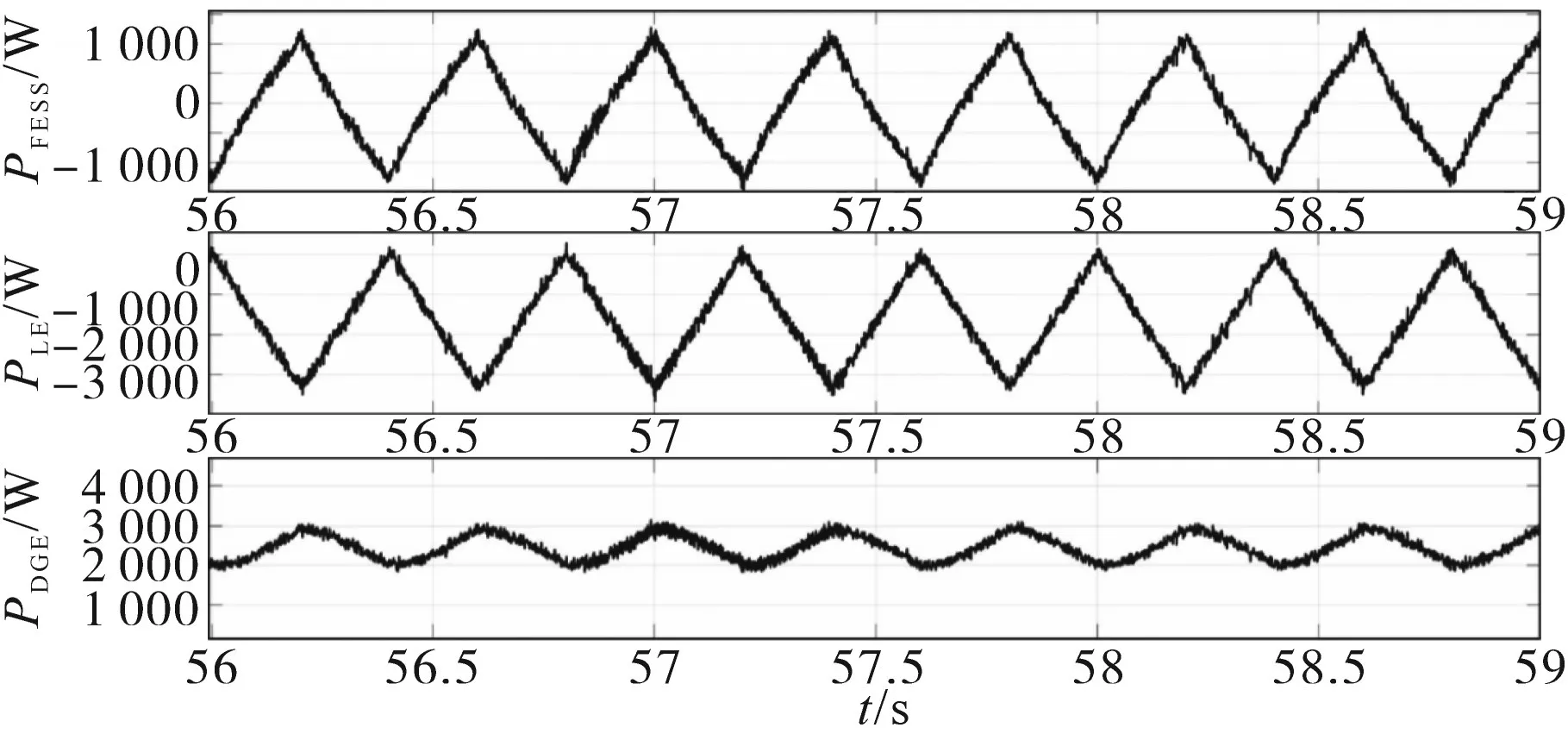
图14 三角周期负载的FESS，LE及DGE有功功率（本文法）Fig.14 Active powers of FESS，LE and DGE for triangular periodic load（proposed control method）

3.2 频率变化分析

在最坏的情况下，阶跃负载变化时的频率变化如图15所示。考虑柴油发电机模拟器的惯性常数为1 s，因此，在场景一中，在无FESS的情况下，DGE的频率下降到49 Hz左右，并在使用调控系统的5 s左右恢复到50 Hz（见图15）。

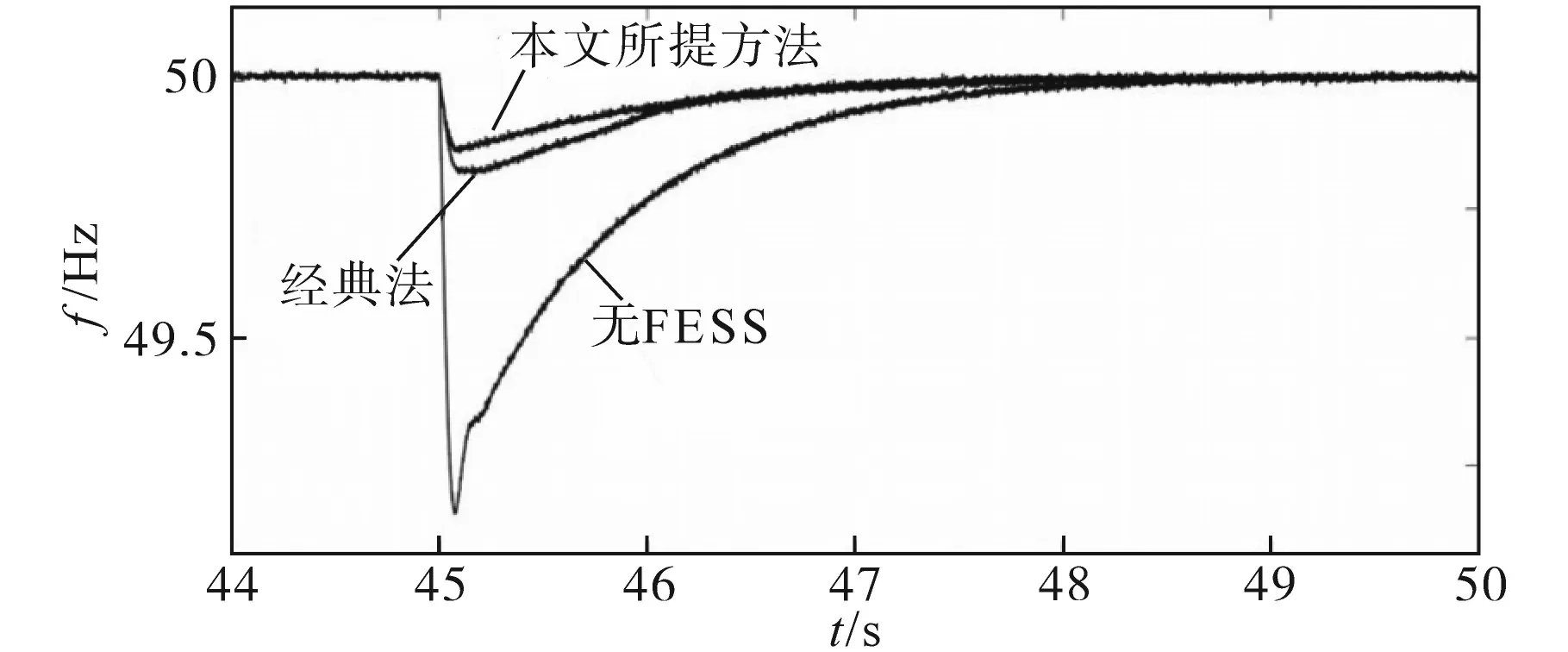
图15 不同场景下阶跃负载的频率变化情况Fig.15 Frequency variations for step load change in different scenarios

从图15可以看出，所提出的FESS控制和经典控制法相比，频率下降显著降低，分别为49.88 Hz和49.81 Hz左右。由于G侧变流器的功率注入速度快，该控制方法的频率下降更小。

图16为本文所提方法和经典方法下直流端口电压随阶跃负载变化的变化情况。由于所提出的M端变流器为三层控制系统，故所提出的控制方法可以减少直流端口电压的波动，而经典方法下当负载发生阶跃变化时，M侧变流器的频率控制回路向解耦回路注入所需的功率并增加其电压，然后G侧变流器的直流端口电压调节器将功率注入到微电网，并恢复直流端口电压到600 V。在该控制方法中，当负载发生阶跃变化时，G侧变流器可以快速提供所需的功率，从而降低直流端口电压。由于三层M端变流器控制系统快速地从IM中提供所需的功率，并恢复直流链路电压到600 V，因此电压降小于传统方法。

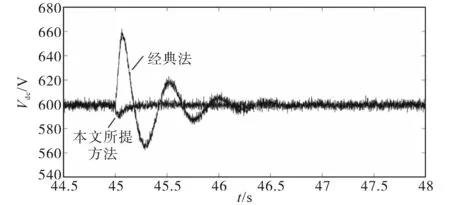
图16 场景2和场景3中阶跃负载变化时的直流端口电压变化Fig.16 DC-link voltage variation for step load change in scenarios 2 and scenarios 3

3.3 直流端口电压分析

直流端口电压的变化可以用来评估所提出的控制系统在FESS运行中启动和补偿模式协调的性能。当FESS连接到微电网，在t∈ [0 s，20 s）期间以飞轮转速控制模式运行。在t=20 s时，工作模式变为补偿模式控制频率。

图17为采用本文提出的控制方法和传统控制方法在模式改变过程中直流端口电压的变化情况。

图17 模式切换过程中直流端口电压变化Fig.17 DC port voltage variation during mode switching

由图17可以看出，使用所提出的模式协调系统，直流端口电压变化明显减少，这就消除了FESS的速度基准的突然变化。

3.4 损耗、延迟和噪声的影响

在实际应用中，FESS的控制系统可能会受到损耗、噪声和延迟的影响。在传统控制方法中（如图3所示），计算微电网频率由G端变流器组成的微控制器，但必须在M端变流器控制器中使用。因此，频率值必须从G端变流器微控制器转移到M端变流器微控制器。这种数据传输可能会导致控制系统的延迟和噪声。与传统的控制方法不同，所提控制方法的频率调节器位于G侧变流器中。因此，频率值不需要从G端变流器转移到M端变流器，这就消除了传输延迟和噪声。另一方面，使用具有150 MHz CPU时钟频率、高带宽和精确的LEM传感器和快速响应IPMs的DSP微控制器，使得硬件和软件的时间常数大约几μs，这与其他时间常数相比是微不足道的。

为了防止噪声对控制系统的影响，在PCB设计中必须注意一些情况，包括多边形的使用，模拟地和数字地在一点上的连接，屏蔽板，电线和连接器，地面阻抗降低使用最佳的地面尺寸和使用屏蔽和屏蔽双绞线铜电缆的信号和电源供应。为了减小电磁干扰噪声，必须使用EMI滤波器。此外，采用线性驱动电路的增量式旋转编码器可以很大程度上保护速度测量免受噪声的影响。在FESS中，总损耗包括无源元件的功率损耗、半导体的开关和传导损耗以及感应电机的损耗（包括飞轮的轴承摩擦）。当飞轮在待机状态下以3 000 r/min的转速旋转时，FESS（G侧变流器的输入功率）的输入功率为215 W。因此，FESS待机模式损耗（也称为自放电）为215 W。从图12可以看出，在负载阶跃变化（t＜45 s）之前，FESS的输出功率为-215 W，这是由DGE提供的FESS备用功率损耗。负载阶跃变化后，微电网的FESS功率损耗是由从微电网传递到微电网的飞轮功率提供的。另外，当FESS功率下降时，备用功率损耗再次由微网提供。

4 结论

本文提出了一种适用于FESS微网的频率控制方法，所提出的G侧变流器控制系统具有更快的功率注入和更低的频率偏差，而M端变流器为三层控制系统，减少了直流端口电压的变化。此外，还设计了一种模式协调系统，使得系统在从启动模式到频率补偿模式的过渡过程中更加稳定。另外，本文还提出了该类微电网的线性化模型，以实现控制器的优化设计。最后，通过实验验证，结果表明该控制方法减小了微电网阶跃负载变化对微电网的频率偏差和FESS直流端口电压的影响；当FESS的工作模式由速度控制模式转变为频率控制模式时，所提出的模式协调系统可以减少直流端口电压的波动。