近距离开采巷道矿压及覆岩运动规律研究

刘晋琦

（山西临汾西山能源有限责任公司，山西 太原 030053）

近距离煤层在我国分布较广，由于下煤层开采受到上部煤层的制约，所以造成下煤层开采较为复杂，同时由于上部煤层开采扰动使得下煤层巷道围岩变形较为严重，所以解决近距离煤层下煤层开采巷道变形成为了近距离煤层开采重要的课题。此前付国华[1]分析了近距离煤层开采覆岩运移特征，给出了一种全新的控制覆岩运移的方法，不仅能够解决现有煤层开采顺槽内错、外错布置的缺点，同时有效解决了下煤层开采巷道变形严重的问题。董兴迎[2]通过研究近距离煤层群采空区下煤层开采矿压规律通过理论分析对下煤层工作面初次来压、周期来压步距等进行分析，为近距离煤层采空区矿压显现规律研究做出一定参考。本文以光道矿为研究背景，对近距离煤层下煤层巷道稳定性进行研究，为近距离煤层开采提供借鉴。

1 矿井概况及模型建立

光道煤矿位于山西洪洞县，矿井面积为15.7 km2，现开采煤层9号，10号，设计年产量120万t。9101工作面主要开采太原组9号煤层，两侧工作面均已完成开采，当完成9101工作面开采后进入9102工作面，由于9102工作面收到上煤层回采的影响，巷道变形较大，为了降低巷道变形，需要对巷道围岩的变形进行研究。在完成上部煤层开采后，下煤层巷道的围岩应力重新分布，当上部煤层进行回采后，此时巷道的底板应力出现变化使得下煤层巷道顶板处于应力叠加区域，造成下煤层巷道顶板变形严重。为了研究下煤层巷道围岩变形情况，选定FLAC3D数值模拟软件对围岩矿压现象情况进行研究。

首先进行模型的建立，根据光道矿9101工作面实际地质条件，建立模型长宽高分别为240 m、200 m和68.4 m，对模型进行网格划分，在进行网格划分时，适当将下煤层巷道进行细化分，便于应力云图的清晰呈现，划分完成后共有174 900个单元，节点共有184 518个。对模型上端部施加覆岩自重，根据计算施加应力为9.2 MPa，对模型的四边进行约束固定，限制四边的垂直、水平方向位移。数值计算的物理模型如1所示。

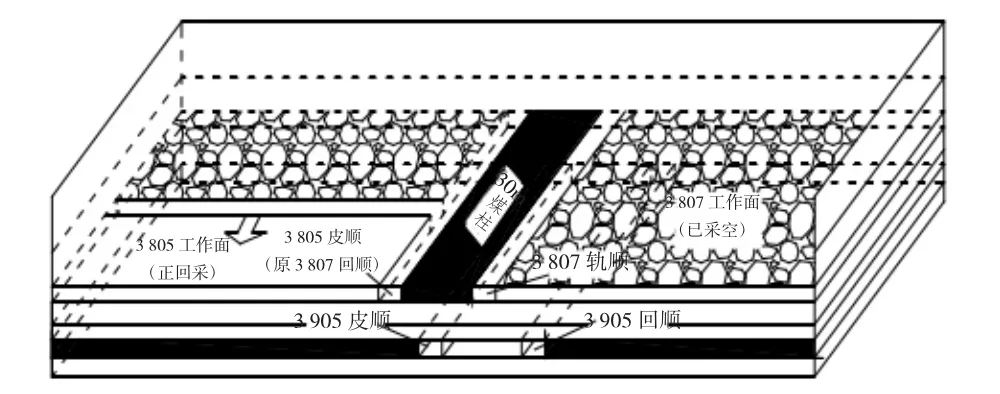
图1 数值计算的物理模型示意图

为了保证模拟计算的精度及准确性，通过力学实验对煤岩的力学属性进行测定，后对模型进行物理参数的设定。物理参数设定如下页表1所示。

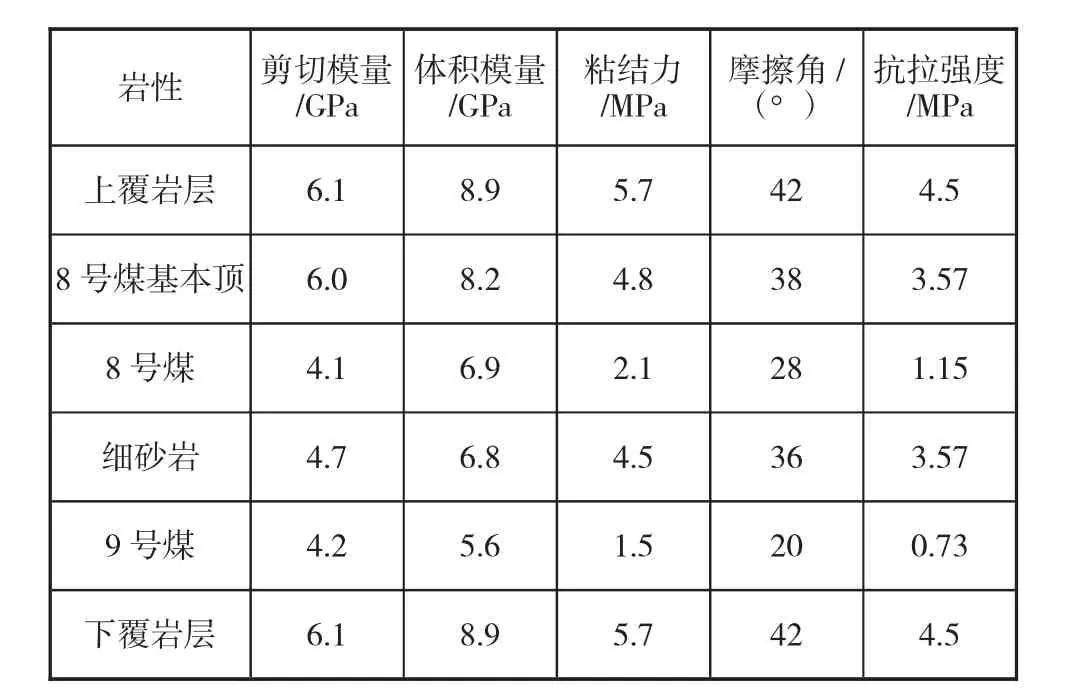
表1 煤岩物理参数参照表

2 模拟分析

完成岩层各参数负值后对命进行力学计算，煤层与采空区交接应力分布云图及底板应力分布如下页图2所示。

如图2-1所示可以看出，煤与采空区交汇处采空区下部出现应力降低现象，在此区域应力值为2 MPa，明显低于原岩应力，而在采空区与煤交汇处的煤下方应力出现集中现象，在煤与采空区交接位置约10 m的距离出现应力最大值为24 MPa，此时应力集中系数为2.4 MPa，由此可以看出在进行下煤层巷道布置时需要将其布设在采空区与煤岩交汇处采空区的下端，同时下煤层巷道的布设方向应当与上煤层巷道类似，这样下煤层巷道的围岩变形大的问题才能从根本解决问题。

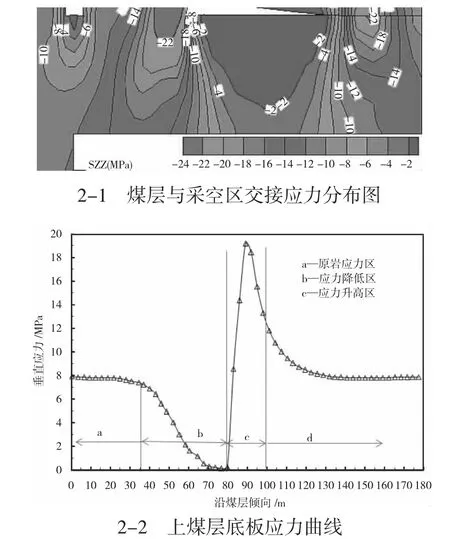
图2 模拟分析图

根据图2-2可以看出，上煤层巷道随煤层走向可分为三个阶段，分别为原岩应力区、应力降低区及应力升高区，在沿煤层倾向0~35 m的区段是属于原岩应力区，沿煤层倾向35~79 m的区段是属于应力降低区，在此区段内底板的应力值小于原岩应力，沿煤层倾向79~99 m的区段属于应力升高区，在此区段内应力集中现象明显，最大的应力集中系数为2.4，沿煤层倾向99~180 m的区段属于原岩应力区，可以看出在进行下煤层巷道布置时，应当避开c区段，使得下煤层巷道布置于b区段。

在进行上部煤层回采时，对下煤层巷道的围岩变形情况进行分析，在巷道沿轴线位置分别布置测站，测站每10 m一个，共设21个测站，同时在每个测站分别布设顶板、底板、两帮位移监测器，同时每个断面布置12个测点，测点布置分别为对角（测点1、测点3）、中线（测点2），分别监测巷道的顶底板及两帮变形，由于测点较多，所以本文仅展示回采距离工作面40 m的围岩变形曲线（如图3所示）。

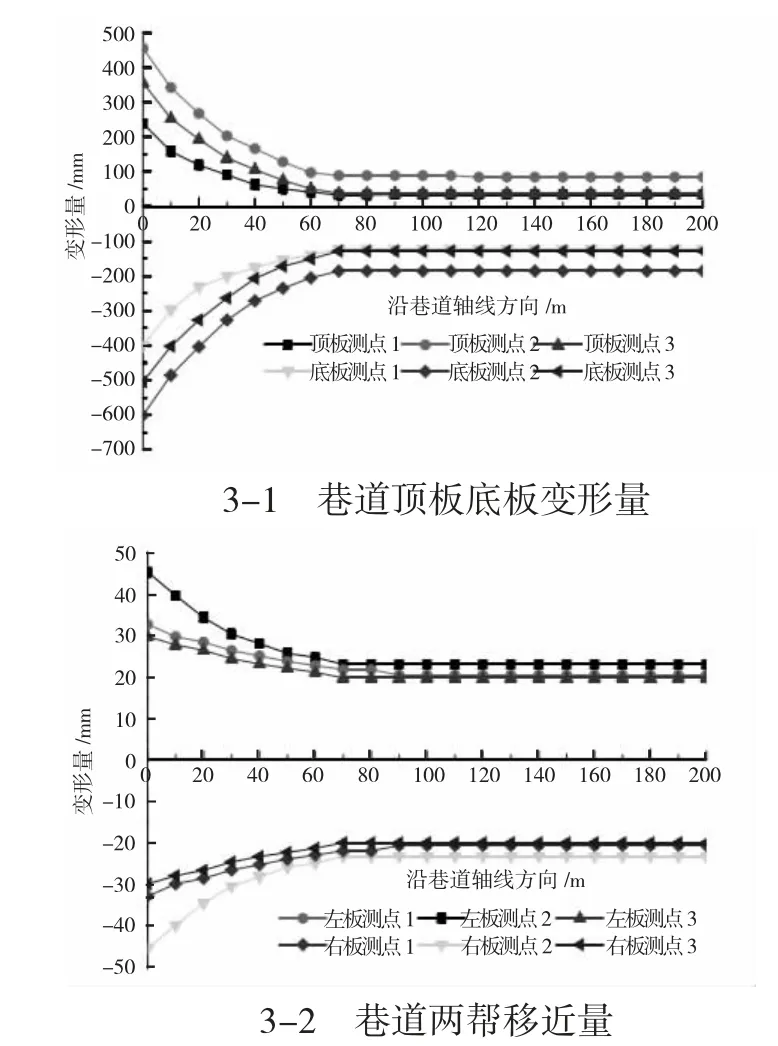
图3 巷道围岩变形曲线

根据研究可知，随着工作面的不断推进，下煤层巷道的变形量逐步变大，当回采至40 m时，此时下煤层巷道变形量最大，此时顶板的下沉量达到452 mm。底板的底鼓量增大至608 mm，两帮的移近量最大值达到92 mm，同时从图3中可以看出，巷道断面的变形大致呈现出对称的特点，巷道断面轴线为巷道中线位置，在测点2位置时巷道变形量最大，而测点1与测点3的变形量几乎类似，同时观察巷道围岩变形量随巷道轴向方向距离的增加呈现先减小后平稳的趋势。根据模拟分析发现当工作面回采距离为0~60 m的范围时，下煤层巷道变形量最大，而当工作面回采大于60 m时，巷道变形量较小，巷道较为稳定，回采对下煤层巷道稳定性影响较小。对距离工作面不同距离下巷道围岩变形进行分析，位移变形曲线（如下页图4所示）。

图4可以看出，当在工作面前方60 m时，巷道顶板下沉量为80 mm，底板底鼓量为116 mm，左帮右帮移近量为41 mm，巷道底板的底鼓量大于巷道顶板的变形量，但两者均较小，所以在工作面前方60 m的范围时巷道不受回采工作面影响，当在工作面前30 m时，巷道顶板下沉量为150 mm，底板底鼓量为215 mm，左帮右帮移近量为45 mm，在此阶段内的巷道变形大于工作面前方60 m的变形量，在工作面后方30 m时，巷道顶板下沉量为595 m，底板底鼓量为711 mm，左帮右帮移近量为63 mm，由于水平应力的剪切作用使得变形量快速增大，在工作面后方60 m时，巷道顶板下沉量为721 m，底板底鼓量为734 mm，左帮右帮移近量为67 mm，在此范围内的变形量均为最大值。由此看出，随着距离工作距离的增加，巷道顶板、底板、两帮变形量均呈现逐步增大的趋势。

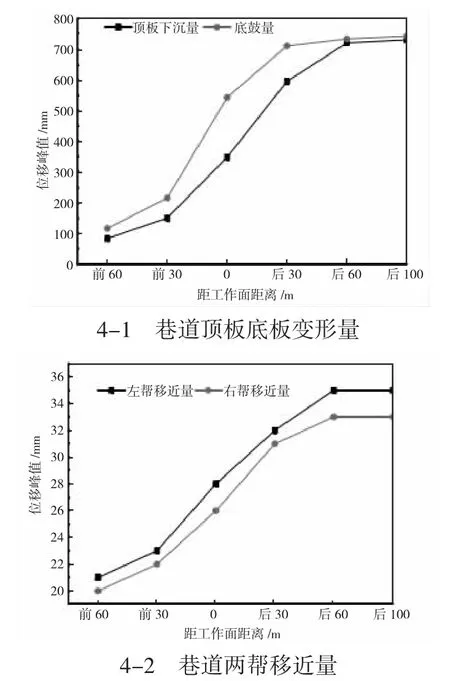
图4 巷道表面位移变形曲线

3 结论

1）通过对煤层与采空区交接应力分布及底板应力分布进行模拟分析，确定了下煤层巷道的合理布置范围。

2）根据模拟分析发现当上煤层工作面回采距离为0~60 m的范围时，下煤层巷道变形量最大，而当工作面回采大于60 m时，巷道变形量较小，巷道较为稳定。

3）通过模拟发现，随着距离工作距离的增加，巷道顶板、底板、两帮变形量均呈现逐步增大的趋势。