ARIMA-RF 组合模型的销售预测研究

袁 远，郭天添

（江苏科技大学 计算机学院，江苏 镇江 212100）

0 引言

随着人们消费水平的提高，服装行业的销售量呈爆炸式增长，这些数据中往往隐藏了大量有价值的客户信息。企业要想维系新老客户的关系，掌握客户需求，就要从这些数据中获取用户喜好，从而更有效地预测客户期望并及时作出反应。因此，从海量信息中获取有价值的数据并加以利用成为企业提高核心竞争力的必要手段之一［1］。

销售预测研究具有一定的商业应用价值和学术研究价值。销售预测不仅能帮助企业合理制定销售计划、去除库存，还能减少不必要的支出，提升利润空间。在为企业创造利润的同时，可避免大量不必要的资源浪费。因此，销售预测一直都是研究热点，很多学者对销售预测方法进行了研究，并提出一系列改进方法，以提高预测的准确性，如文献［2］通过时间序列模型ARMA 先进行月预测，然后通过PERT（计划评审技术）获得月预测的期望值，再对两者结果进行加权，得到最终预测结果；文献［3］通过使用鲁棒损失函数和小波核函数解决数据集呈正态高斯分布以及幅值波动较大的问题，以有效减少销售时序中的噪音和奇异点问题，并增强其鲁棒性；文献［4］通过对历史销售数据特征的观察，发现其包括线性和非线性两部分，结合AR⁃MA 模型预测数据集的线性部分和BP_AdaBoost 模型预测数据集的非线性部分，然后叠加两者预测结果作为新的预测值，可避免ARMA 模型预测精度低的问题，同时解决了神经网络模型导致局部极小值的问题。销售预测的核心算法一直在改进，通过阅读国内外文献，发现相关算法在销售预测方面存在的问题，并对其进行改进，对于提高销售预测模型质量与预测准确性具有重要意义［5］。本文通过学习与借鉴国内外文献，采用时间序列模型中预测效果较好的ARIMA 模型对线性信息进行预测，然后利用对非线性信息学习能力较强的随机森林对ARIMA 模型预测残差进行矫正，通过构建ARIMA-RF 组合模型对历史销售数据的线性和非线性特征进行预测。

销量预测方法通常可分为定性分析法与定量分析法，目前主流预测算法包括神经网络算法［6］、遗传算法［7］、时间序列算法［8］、随机森林算法等［9］。本文采用结合时间序列算法中自回归综合移动平均模型与随机森林模型的组合模型，根据历史数据进行销售预测［10-11］，利用随机森林算法较强的线性学习能力优化时间序列模型的预测结果残差。通过构建的组合模型与单个模型对比结果，发现组合模型的预测结果更加精确。

1 相关理论

1.1 ARIMA 模型

ARIMA（自回归—滑动平均混合模型）是一种时间序列方法［12］。ARIMA 是包括非平稳情况的ARMA 模型，也是对ARMA 模型的扩展。由于销售数据受节假日、电商节等因素影响，历史销售数据并非相对平稳的时间序列数据，实际场景下很多序列因为与社会经济和商业有关，从而表现出非平稳行为，包含趋势和季节模式的序列在本质上也是非平稳的，因此提出了ARIMA 模型，通过应用数据点的有限差分处理使序列平稳化，并把移动平均模型、自回归模型与差分法相结合，从而得到ARIMA 模型（p、d、q）。p、d和q 为整数，分别为ARIMA 模型的自回归、进行差分的阶数和移动平均，具体公式如式（1）所示。

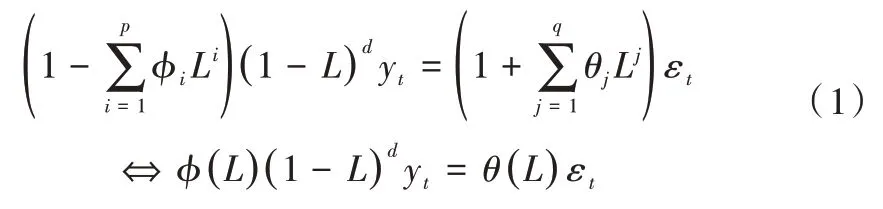
其中，L 是滞后算子，d∈ℤ,d>0。

虽然ARIMA 模型可能在某些特殊情况下表现不佳，但其可在构建过程中进行优化，以体现针对不同时间序列的灵活性，仍使其成为一种非常优秀的预测方法［13］。ARIMA不仅考虑了数据特征在时间序列方面的规律性，而且减轻了其他影响因子对实验结果的影响，所以ARIMA 模型针对长短期预测结果的准确率都表现较为优异［14］。其中心思想是把历史数据集的时间序列作为变量，其取值随着时间而变化，虽然某个时间序列的值具有不确定性，但从宏观角度来看，完整的时间序列还是表现出一定规律性。因此，首先将不平稳的时间序列转换为平稳的时间序列，然后通过因变量对模型的滞后值、随机误差项值和随机误差项的滞后值进行回归［15］。建模公式如式（2）所示。

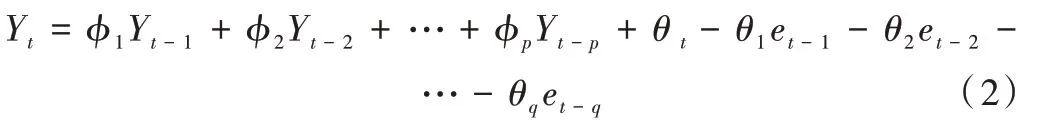
其中，φ表示AR 的系数，θ表示MA 的系数，其建模流程如图1 所示。

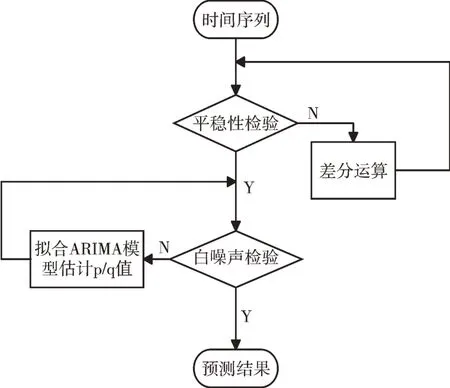
Fig.1 Time series ARIMA modeling process图1 时间序列ARIMA 建模流程

首先进行平稳性检验，通过对时间序列散点图的观察初步进行判断；然后进一步对单位根进行检验，判断其是否平稳，若不平稳则需要利用差分等方式将其平稳化；之后进行模型识别与定阶，确定滞后系数和模型。可通过检验模型残差序列［16］判断其有效性，因为在模型构建过程中，容易在滞后项阶数选择时出现偏差。模型构建完成后，再根据历史销售数据预测未来一段时期的销售量。此外，通常会利用一些固定指标对模型进行判断。ARIMA（p，d，q）模型的判断指标为AIC，具体公式如式（3）所示。

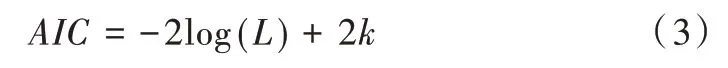
式中，L 为极大似然估计值，惩罚函数为2k，如果模型中有截距或常数项，k=p+q+1，否则k=p+q。

1.2 随机森林模型

随机森林模型通过训练多棵决策树，将每棵决策树的投票结果汇总作为预测值，其中每棵树都是基于一个独立随机向量的值产生的［17］，森林中每棵树的建立都涉及两次随机过程：第一次随机过程是在训练集构造过程中使用Bootstrap 方式从原始数据中进行有放回的抽样，这样获得训练集的最大特点在于有一部分数据会重复出现在训练子集中，有一部分则不会出现，不会出现的这部分数据称为袋外数据OOB（Out-of-Bag），大概占到原始数据的三分之一，也被用来估计森林的强度和相关度；第二次随机过程在于特征选择的随机性，在基分类器决策树构建过程中不断从所有属性特征中选择一部分按照一定衡量标准进行排序，组成决策树的每一个节点，从而大大增加了决策树构建的随机性。两次随机过程带来的优势在于：第一次随机过程使得构建的决策树对数据有了不同侧重点，保证树与树之间尽可能相对独立；第二次随机过程使得每棵树的特征组合呈现多样性，基分类决策树对不同特征有了不同的关注度，更能作出准确判断［18］。两次随机性的加入，使得随机森林能够防止过拟合情况出现，模型泛化能力更强，对噪声更具鲁棒性，从而使整体预测精度得以提升。

随机森林模型是对多棵决策树的集成算法，模型利用Bootstrap 随机抽样以及节点随机划分完成对多棵决策树的构建，然后由这些决策树进行投票，以投票结果作为最终分类或回归结果。主要流程如图2 所示。

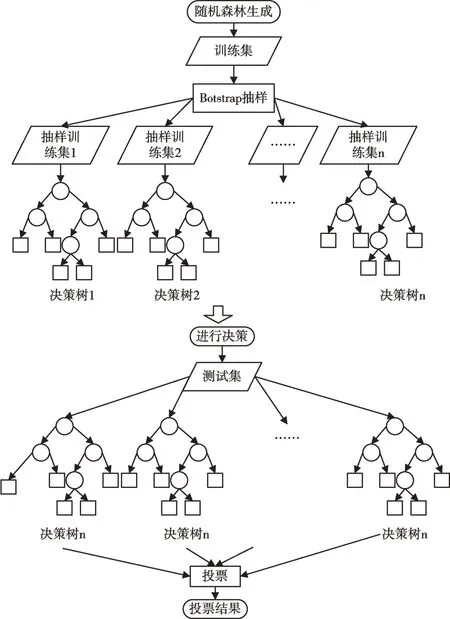
Fig.2 Random forest generation and decision process图2 随机森林生成及决策流程

Gini 系数是随机森林的重要性度量指标［19］。每棵决策树投票结果都为其所对应特征的投票结果，在解决分类问题时，以Gini 系数和信息增益划分特征值，而处理回归问题时，则采用最小二乘拟合法或计算方差法划分数据集中的特征。Gini 系数衡量树节点的不纯性公式如式（4）所示。

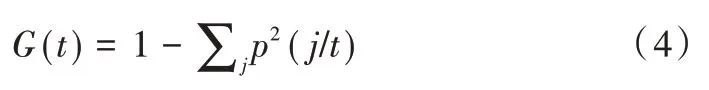
其中，t为决策树节点特征，p2(j/t)表示j类目标在其对应节点的比例。最小二乘偏差法适合回归树构建，误差公式如式（5）所示。

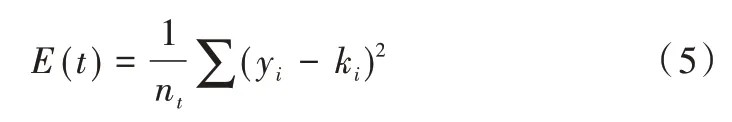
式中，nt为节点数据实例数，kt为实例数据目标值，kt=(∑yi)/nt，节点t的最小二乘偏差标准为使式（6）最大。

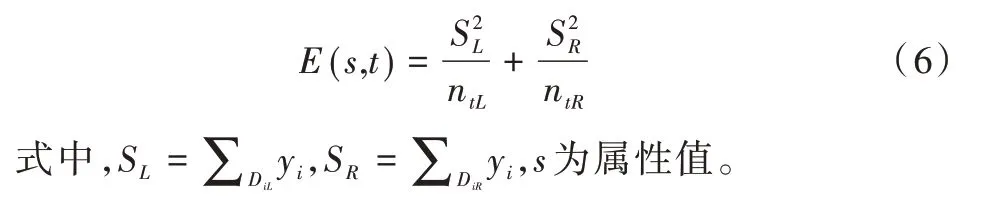
2 组合模型

2.1 组合模型原理

对于现实背景下的问题，组合模型通常可提高预测结果的准确率［20］。常见组合模型方法有：①平均法。对于组合模型中的输出值取平均值；②投票法。根据模型对应的投票数决定是否采用该模型或对多个模型进行组合等［21-22］。时间序列模型受非线性特征及随机变量等影响因子影响较大，而对于商家地理位置、外部天气情况、客流量等非线性信息无法很好地进行处理，所以大部分时间序列预测模型都是根据历史趋势预测未来走向。机器学习模型对数据量较大、特征维度较高的历史销售数据能处理得更好，其中随机森林更是经典的机器学习模型，近年来在处理现实背景下的实际问题中具有更好的效果。实验通过对随机森林模型不断调参，增强其学习能力。随机森林模型是从分类拓展到回归应用的集成模型，其按照输入的最小误差进行划分，对于外部天气情况、是否节假日、客流量等非线性特征的影响更为重视，而这些影响体现在时间序列预测模型残差中，需要对ARIMA 预测模型残差进行优化，以提高实验模型的预测准确度。

ARIMA 模型对于特征维度多、需要预测未来较长时间周期的情况相比其他时间序列模型表现更佳［23］，因此本文选择ARIMA 时间序列模型预测销量，并对其品牌的历史销量数据进行预测分析。随机森林模型在机器学习模型中的表现也尤为出色，可综合两者优势组合成ARIMA-RF 模型以提高预测精度。

2.2 ARIMA-RF 组合模型设计

整个组合模型主要分为以下几部分：数据预处理、ARIMA 模型预测、随机森林训练和ARIMA 预测数据矫正。组合模型设计如图3 所示。

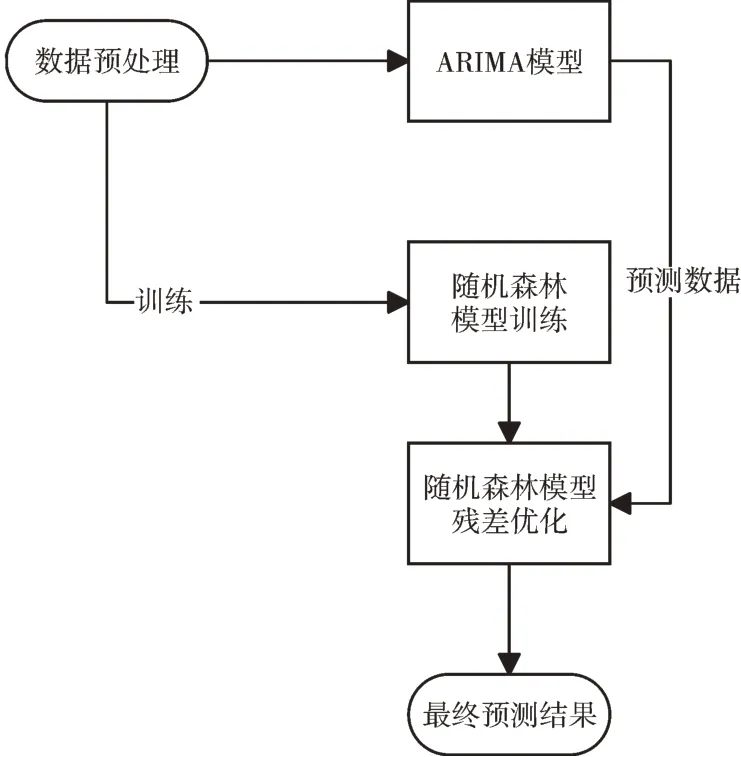
Fig.3 Combinatorial model design图3 组合模型设计

首先在数据预处理部分，对于销售预测而言，一批干净、完整的优良数据是保证模型准确、可靠的基石，而获取的历史数据通常不规则，且包含异常值和噪声干扰，因此需要事先对现有数据进行一系列预处理。通过调研业务，深入理解变量间的关系，清洗数据集并处理缺失值、离散值和分类变量，并根据数据特征选择合适的模型作小范围的数据验证，之后再针对性地对模型进行优化。首先针对实际业务场景，构建合适的预测模型；然后观察销量突变现象，分析相关影响因子；最后处理异常离散值，降低不良影响。取数据集中2015 年一整年的测试数据观察销售量时序分布情况，如图4 所示。

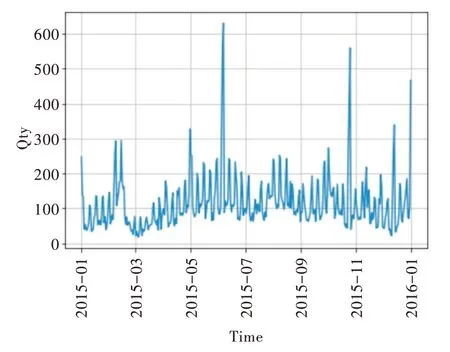
Fig.4 Time series distribution under day dimension图4 以天为周期维度的时间序列分布

通过观察发现，以天为统计周期的历史销售数据过于分散，天与天之间并没有明显的周期性特征，难以捕捉相关规律。出于对业务数据的理解，考虑挖掘以周为循环周期的变化趋势。对于周的划分，在销售时间上将销售数据的日期换算成对应农历周。这是由于服装与其他快销产品不同，其销售情况受温度季节影响较大。而农历24 节气对应地球公转周期，农历周相比公历的月份周更能准确反映不同阶段的气温变化，这在以年为周期维度拟合趋势时能更明显地体现出隐藏的温度变化趋势。因此，新建农历周换算表，映射具体date 对应的农历周份。

ARIMA 模型预测则是将历史销售数据的n 个特征用时间序列表示，针对这些历史时间序列进行特征根校验，在判断平稳性后构建AIC 指标最小时的ARIMA 模型，预测未来某一阶段的时间序列集合，最后计算模型预测结果与实际值的误差。之后，通过训练随机森林模型对误差值进行矫正优化，在随机森林训练过程中，可发现特征之间的联系，从而判断哪些特征对预测结果的影响微乎其微，并将这些无关特征值去除。最后通过实验发现，一些重要特征对预测值影响较大，数据特征相关图如图5 所示，其中像素块越红，代表相关性越强。

实验最后通过训练完成的随机森林模型提纯ARIMA模型的误差值，修正ARIMA 模型预测结果，得出新的预测值，根据本文设计好的评价指标对比单个实验模型预测结果，以期达到更高的预测精度。

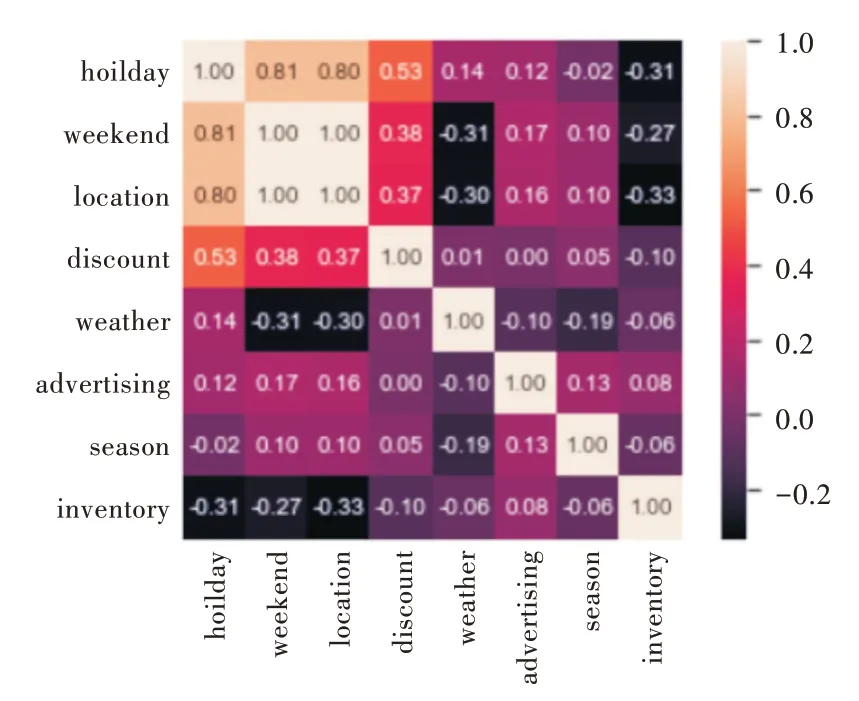
Fig.5 Data feature correlation graph图5 数据特征相关图

3 实验与分析

3.1 实验数据处理

本文以某快销服饰品牌上海门店2015 年1 月-2019 年12 月的实际销售数据作为分析数据，同时利用Python 通过网络爬虫从国家气象局网站抓取了上海市2015 年1 月-2019 年12 月的历史天气数据。基于上述数据建立预测模型，预测该品牌在上海市未来一年每日的销售数据。企业可根据预测数据优化运营，降低库存与成本，并提升流程效率。原始数据如表1 所示。每条数据都是一件服装完整的销售记录，例如sku 标识了服装唯一id，color 标识颜色，season 标识服装目标售卖季节，salenum 标识服装售卖件数，tag_price 标识吊牌销售价格，saleprice 标识实际销售价格，以及产品库存、是否节假日、是否为电商款等多种属性。将2015-2018 年的数据作为训练集，2019 年全年的数据作为测试集。训练集用来对组合模型进行训练，测试集的预测结果用来与真实销售数据进行销量对比分析，从而计算组合模型的预测精度。

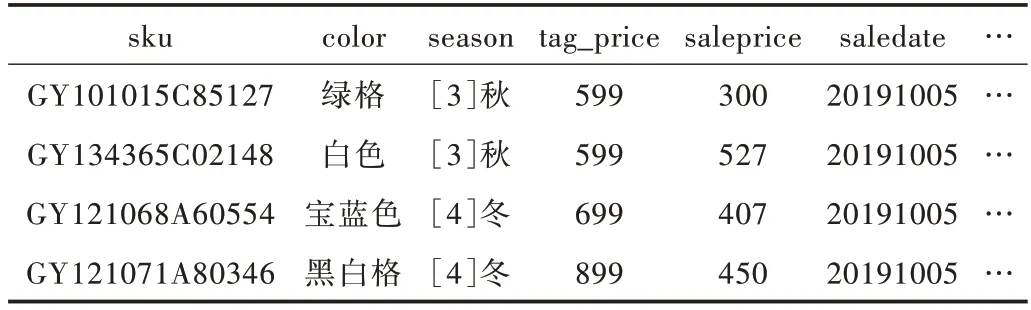
Table 1 Raw data overview表1 原始数据概览

3.2 评价指标

模型建立后需要通过一定方法进行评估，以衡量该模型是否高效。在实际应用中，通常将验证数据集代入模型中运行，获取实验结果并与实际值作比较，根据不同指标衡量模型表现，以此评估模型优劣。通常采用如下指标：

（1）平均绝对误差。MAE（平均绝对误差）表示预测结果与实际结果之间差值绝对值的平均数，该评价指标是对绝对误差损失的预期值。计算公式如式（7）所示，其中a代表预测值，b代表实际值。

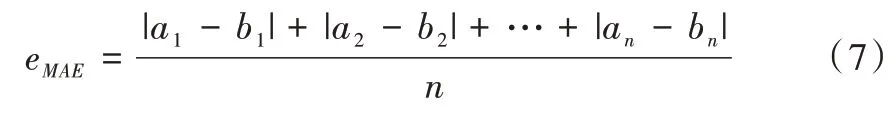
（2）均方根误差。RMSE（均方根误差）表示预测结果与实际结果误差的平方同序列长度之比的平方根，该指标对应于平方误差的期望。计算公式如式（8）所示。

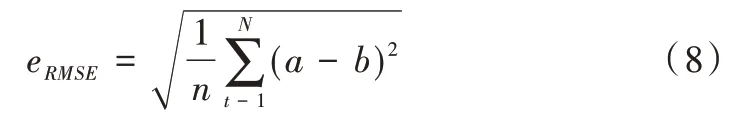
其中，n 为预测序列长度，a 为真实销售数量，b 为预测值。虽然RMSE 可以评判模型预测结果平方误差大小，为衡量模型优劣提供一定的科学依据，但其不能作为衡量模型优劣的决定性指标，理应同时考虑其他指标情况，综合比对模型，从而得到更具说服力的结论。

3.3 实验结果对比

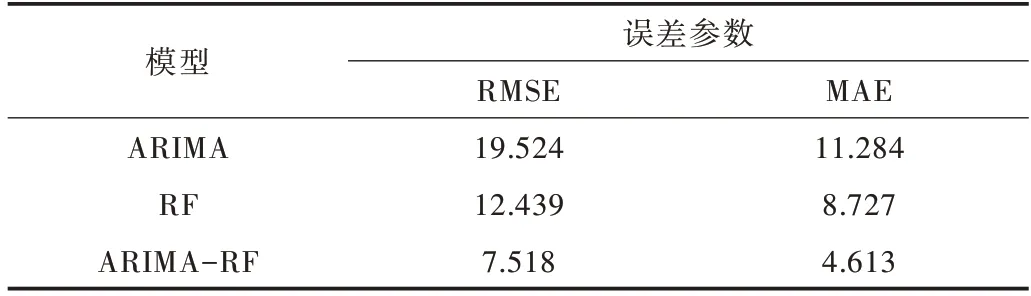
Table 2 Comparison of prediction results of different experimental models表2 不同实验模型预测结果比较

从表2 中可以看出，ARIMA-RF 组合模型相比单一模型，平方绝对误差与均方根误差都有所下降，销量预测精度总体上优于单一模型。说明ARIMA-RF 组合预测模型发挥了两种模型的优势，相较于单一模型预测效果更佳，更适用于本文的商业环境。

4 结语

本文以某快销服饰品牌上海门店近5 年的销售数据为基础，依次构建了RF 模型、ARIMA 模型以及优化后的ARI⁃MA-RF 组合模型。在相同数据集的基础上通过实验比较预测结果的各项评价指标，发现ARIMA-RF 组合模型的RMSE（均方根误差）和MAE（平均绝对误差）均优于单一模型的实验结果，证明了ARIMA-RF 模型对于商业环境下的服饰销售预测具有更高精度，同时分析其实用性，以期在更多领域加以应用。由于实际销售情况会受到很多其他外界情况影响，所以实验效果还存在进一步提升的空间。