基于CAE-DNN 的多工序质量预测方法
杨 静,董宝力
(浙江理工大学机械与自动控制学院,浙江杭州 310018)
0 引言
传统产品过程质量管控以抽样检查和统计方法为主,存在管控滞后问题,无法根据监测到的过程质量数据及时反馈产品信息[1]。随着产品复杂度提高,过程质量数据急剧增多且存在噪声数据[2]。针对多工序生产过程质量数据的多特征、多噪声特性[3],建立产品质量预测模型,可以更好地利用产品过程质量数据对生产过程进行实时监控与分析,对保证产品生产质量具有重要意义。
多工序质量预测研究较多,梳理出以下研究内容:针对加工样本数据不足和加工误差难监测等问题,研究赋值型误差传递网络多工序加工质量预测方法[4];采用PSO 算法优化支持向量机参数,用于质量预测模型的寻优[5],但该方法未考虑数据本身对模型性能的影响;在多工序质量预测中采用尺寸关联和偏最小二乘算法提取关键特征[6],但未考虑数据噪声和小样本问题;针对数据特征复杂、高维、多噪声和异常值等问题,采用PCA 与改进的RNN 构建产品质量预测模型[7];考虑数据类型的不同,在质量预测模型训练阶段采用半监督堆叠自编码器(SS-SAE),自适应调整训练策略[8]。多工序质量预测需要综合考虑过程质量数据,但针对多特征、多噪声的研究较少。
深度学习是产品质量预测的一种机器学习方法,利用深度置信网络(DBN)进行无监督特征学习,将学习到的特征输入质量预测模型[9];采用DFAEs 进行无监督学习,完成轴承故障模式识别[10];采用Autoencoder-BLSTM 混合模型,对航空发动机寿命进行预测[11]。以上研究中未考虑数据噪声问题,不适于多工序过程质量预测。
本文以多工序制造为研究对象,针对多工序制造过程质量数据多特征、多噪声特性,提出一种基于收缩自编码器—深度神经网络CAE-DNN 的质量预测模型。通过训练CAE 特征提取原始数据中存在的噪声,提升DNN 预测模型的鲁棒性,增加BN 层、Dropout 和L2 正则化。以天池TFTLCD(薄膜晶体管液晶显示器)的生产过程质量数据为例,研究建立多工序质量预测模型。TFT-LCD 生产及工序复杂,产品关键工序影响因素众多。同时,由于过程质量数据测量、采集精度、设备工况漂移等因素,不可避免地产生大量噪声数据。由于生产过程相对稳定,采集到的过程质量数据较为相似,有效样本少。因此,在多工序的过程质量预测研究中,需要重点研究过程质量数据的多特征、多噪声等问题。
1 收缩自编码器
自编码器[12]是一种基于无监督学习的神经网络,可将高维数据映射为低维数据,相关研究表明自编码器亦可用于数据降噪[13-14]。自编码器主要由编码网络和解码网络构成,层级结构包括输入层、隐藏层和输出层,隐藏层输出即为压缩后的特征,其拓扑结构如图1 所示。
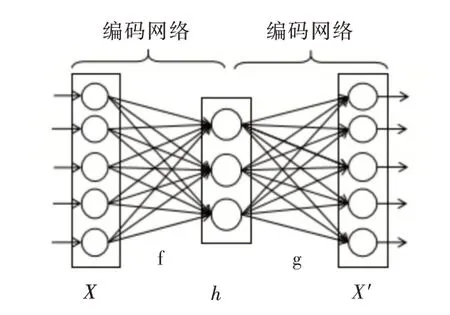
Fig.1 Autoencoder network structure图1 自编码器网络结构
编码网络对输入的过程质量数据X进行编码,得到编码特征h,解码网络将h解码为X',期望重构出原始输入X,公式如下:

其中:f 和g 为激活函数。
收缩自编码器(CAE)由Rifai 等[15]提出,它在普通自编码器的损失函数上添加了一个正则惩罚项。相较于其它类型的自编码器[16-17],CAE 不仅可以很好地重建输入信息,而且对一定程度下的扰动具有不变性[18],即能够减少模型对噪声数据的敏感性,使得模型具有更强的鲁棒性。CAE 主要是通过惩罚隐藏层表达式的Jacobian 矩阵的F 范数来达到抑制数据噪声的目的,公式如下:

收缩自编码器目标函数如下:
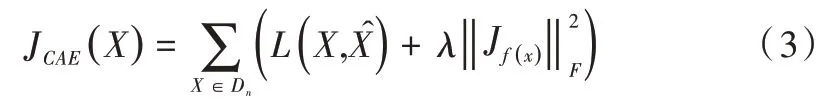
其中:L为均方差损失函数,λ为控制惩罚力度的超参数。
2 CAE-DNN 混合质量预测模型
CAE 的预训练是一个不断学习数据特征、进行特征提取的过程,同时也为DNN 提供合理的初始参数。如图2 所示,在CAE 完成预训练后,对CAE 的权重和偏置初始化,最后一层网络参数随机初始化,利用特征提取层提取的特征完成过程质量预测。在过程质量预测模型训练中采用反向传播算法微调网络参数,提高预测模型性能。本文在预测模型训练阶段对整个网络的参数进行优化,加快网络训练速度,避免只对最后一层网络参数进行调整而陷入局部最优解。

Fig.2 CAE-DNN hybrid model structure图2 CAE-DNN 混合模型结构
由于神经网络的复杂性以及数据集中存在噪声数据,在训练过程中经常会发生过拟合现象,导致网络模型在训练集上的精度远远高于测试集,且网络模型越复杂越容易发生过拟合现象。为降低DNN 的复杂度,改善DNN 的过拟合现象,本文加入BN(Batch Normalization)层、Dropout 和L2 正则化。
(1)BN 层也是网络中的一层,能够将隐藏层输出分布强制转换为均值为0、方差为1 的标准正态分布,使得非线性激活函数的输出值处于输入比较敏感的区域,从而避免发生梯度消失问题[19]。
(2)Dropout 在深度学习网络训练过程中,将神经网络的神经元按照一定概率从网络中丢失[20-21]。Dropout 一方面简化神经网络结构,减少训练时间,另一方面每个神经元都以一定的概率出现,使两个相同的神经元不能保证同时出现,权值更新不再依赖于固定神经元的共同作用,改善了DNN 的过拟合现象。
(3)L2 正则化是在原始损失函数基础上添加一个正则项,即各层权重Wj的平方和,使显著减少目标值方向上的参数相对保留完好,对无助于目标值方向上的参数在训练过程中因正则项而衰减。
由于特征参数的量纲各不相同,为了消除不同量纲对模型性能的影响,在数据输入模型前要对数据作归一化处理,将数据映射到0~1 之间,公式如下:

其中,xi,j为第i个输入样本的第j个特征值分别为样本数据中第j个特征的最大值和最小值,xnorm为归一化后的特征。
3 实例分析
3.1 数据集说明
本文选取天池工业AI 大赛—智能制造质量预测中关于TFT-LCD 的过程质量数据。数据包含各工序的机台温度、气体、液体流量、功率、制成时间等因子。过程质量数据总共500 样本,合计8 029 个字段,表1 是其中部分质量预测数据。第1 个字段为ID 号码,TOOL_ID 字段表示使用的机台种类,剩余字段的名字用于区分不同工序,字母X 前的数字表示工序编号,X 后的数字表示该工序中的参数编号,如210X1 表示210 工序中的第1 个参数。

Table 1 Example of experimental data表1 实验数据示例
3.2 数据集处理
数据处理使用Python3.7、Sklearn 和TensorFlow2.2 等工具。对样本数据整理发现,过程质量数据集存在大量的重复数据、单一值以及大量缺失值,需对数据进行一定的预处理。
在Python3.7 环境下,借助Pandas 模块处理异常值、去除重复字段、单一值字段和缺失值字段。如对数据中存在突然增大和较小的值采用均值进行填充和替换,如图3(a)所示,处理后的数据分布如图3(b)所示。此外,用来表示机台的字段采用One-hot 编码数值化。上述预处理后的有效特征变量为3 353 个。
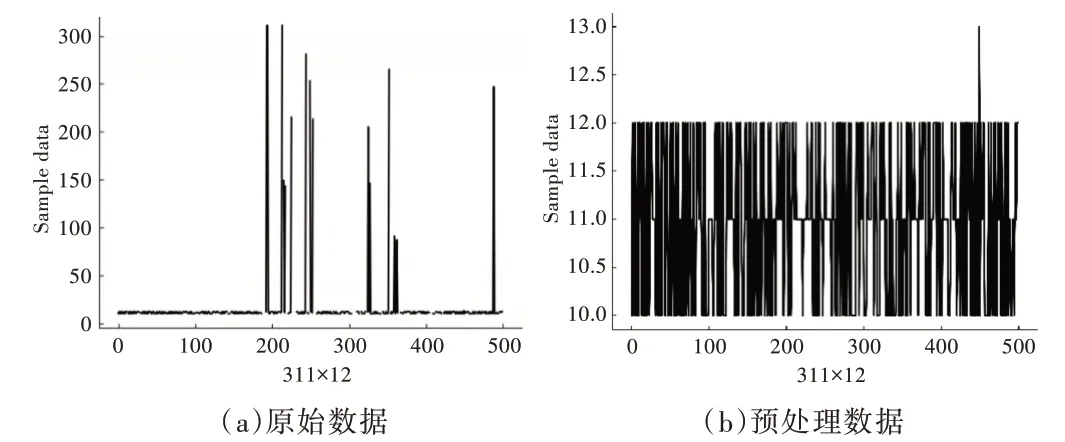
Fig.3 Feature data distribution图3 特征数据分布
3.3 参数设置
经预处理后的有效特征为3 353,随机选取400 条数据作为训练集,剩余数据作为测试集。对划分后的数据集进行反复试验,最终选择CAE 网络结构为{3 353,1 600,500,64,500,1 600,3 353},学习率lr=1×10-4,惩罚力度参数λ为0.05,批尺寸bach_size=50,迭代次数epochs=5 000,DNN 的网络结构为{3 353,1 600,500,64,16,1},学习率lr=1×10-4,Droptout 数据特征保留率keep_prob=0.9,批尺寸bach_size=50,迭代次数5 000。本文采用激活函数Relu,评价指标采用均方误差(Mean Square Error,MSE),公式如下:
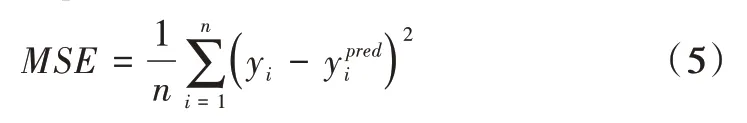
未添加BN 层和全局平均池化层的预测模型为FCAE-DNN,图4 为本文所用模型与CAE-DNN 模型在相同参数条件下的训练过程。实线为训练过程曲线,虚线为测试过程曲线。根据收敛速度,F-CAE-DNN 更具优势,但随着训练次数的增加,F-CAE-DNN 在测试集上的误差有缓慢增加趋势,而CAE-DNN 则趋向于一个稳定值;根据模型的泛化性能指标,CAE-DNN 在训练集与测试集上的MSE值分别为0.015 5 和0.018 3,F-CAE-DNN 的MSE 值分别为0.014 9 和0.027 8,CAE-DNN 在测试 集上的MSE 值小于后者,具有更好的泛化性能。
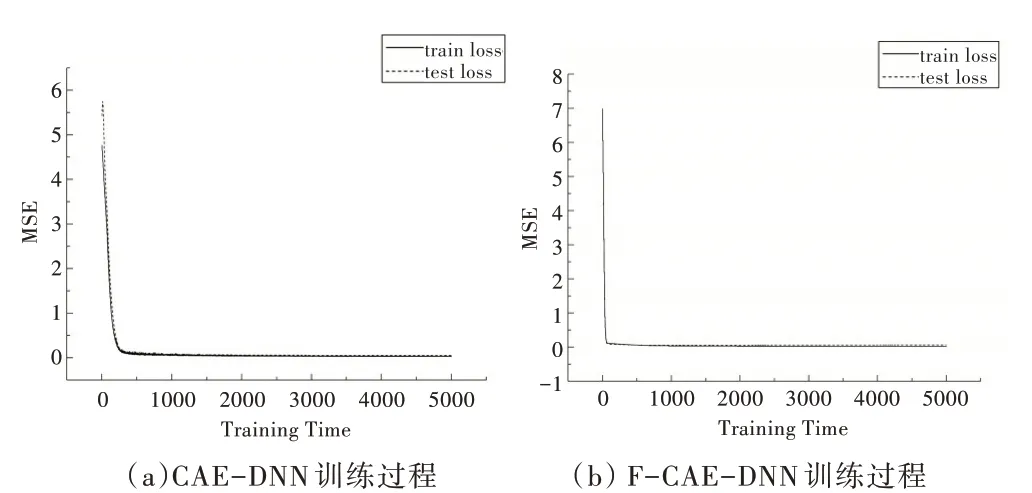
Fig.4 Training process comparison图4 训练过程比较
预测模型训练完成后,将测试数据集输入模型进行验证。预测结果如图5 所示,其中实线表示测试样本的实际值,虚线表示测试样本的预测值,从图中可以看出预测值与实际值非常接近,模型预测精度较高。
3.4 结果比较
为了定量分析模型性能,本文采用均方误差(MSE)和每百个样本的预测速度(每百个样本预测耗时)进行模型对比。将上述实验结果分别与自编码器—深度神经网络(AE-DNN)、深度神经网络(DNN)、PCA-BP 神经网络、PCA-SVR 进行比较验证。
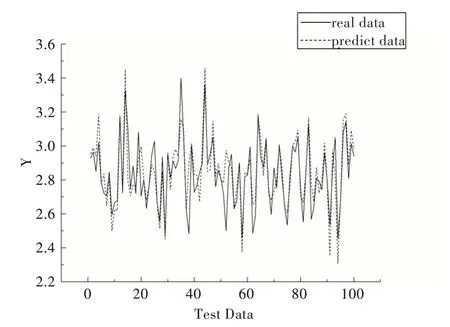
Fig.5 Comparison of CAE-DNN quality prediction results图5 CAE-DNN 质量预测结果比较
(1)在AE-DNN 中,AE 的损失函数中无正则惩罚项,其它层与CAE 对应层相同,隐藏层采用Relu 作为激活函数。
(2)在DNN 中,无预训练,隐藏层采用Relu 作为激活函数。
(3)在PCA-BP 中,降维后的数据维度设置为64,BP 网络全连接层数设置为3 隐层,激活函数使用Relu,各层节点数为{64,16,1}。
(4)PCA-SVR 中,降维后的数据维度设置为64,选用高斯核函数,采用网格搜索寻找最优参数并使用5 折交叉验证,超参数设置为{C=0.1,gamma=1}。
不同模型预测结果分别如图6—图9 所示,不同实验方法结果对比如表2 所示。
从图6—图9 可知,与其它4 种预测模型相比,CAEDNN 的样本实际值(实线)与预测值(虚线)拟合程度最好,表明其预测精度最高,PCA-SVR 实际值与预测值偏差最大;由于噪声数据影响,与CAE-DNN 对比的4 种模型存在部分实际值与预测值有较大误差情况,而CAE-DNN 每个样本预测结果都比较精确,抗噪声能力较强。表2 的模型预测性能评价指标反映出CAE-DNN 与其它4 种模型对比具有较好的预测精度。
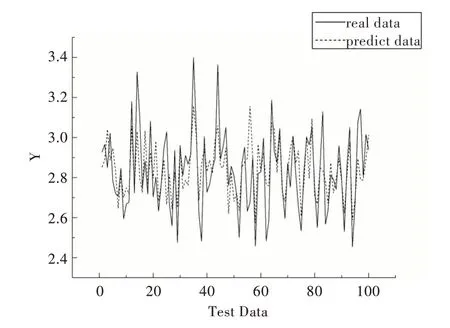
Fig.6 Comparison of AE-DNN quality prediction results图6 AE-DNN 实际值与预测值对比
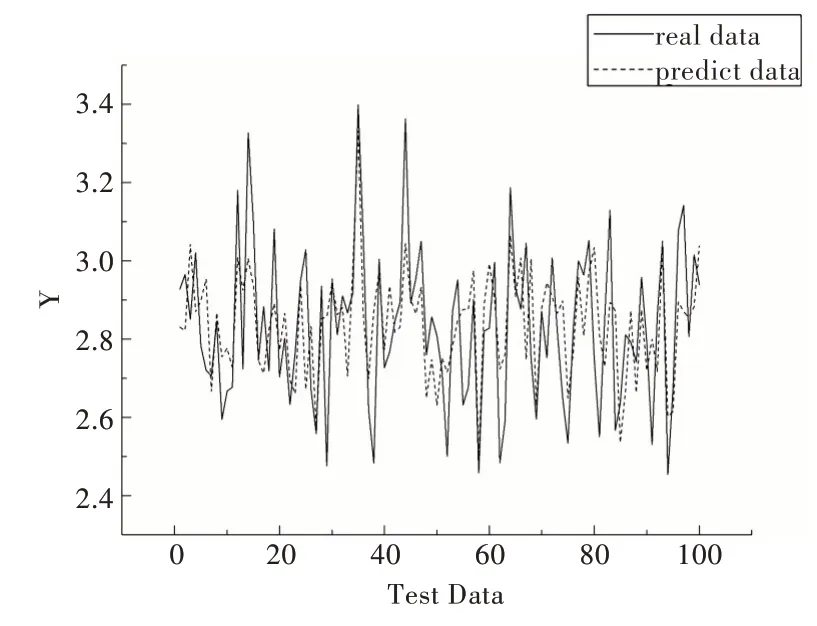
Fig.7 Comparison of DNN quality prediction results图7 DNN 实际值与预测值对比
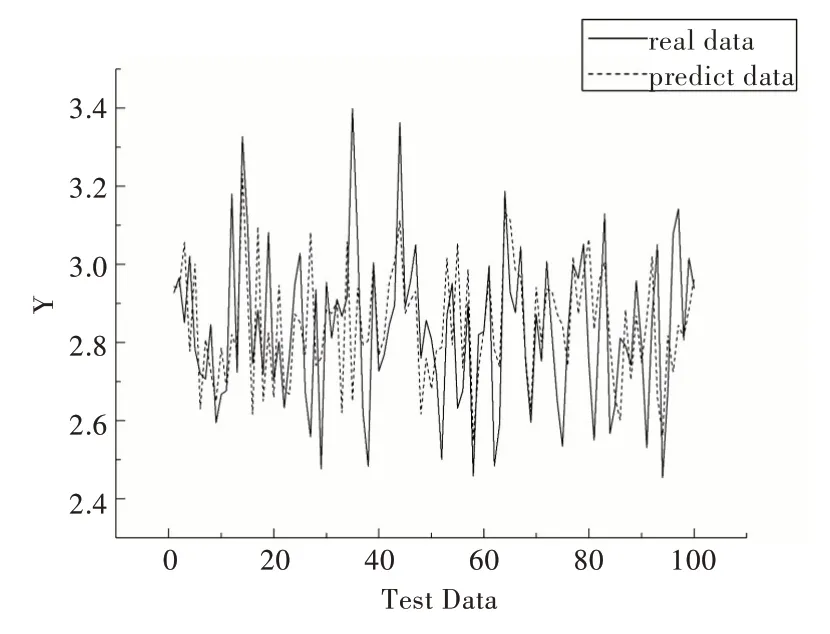
Fig.8 Comparison of PCA-BP quality prediction results图8 PCA-BP 实际值与预测值对比
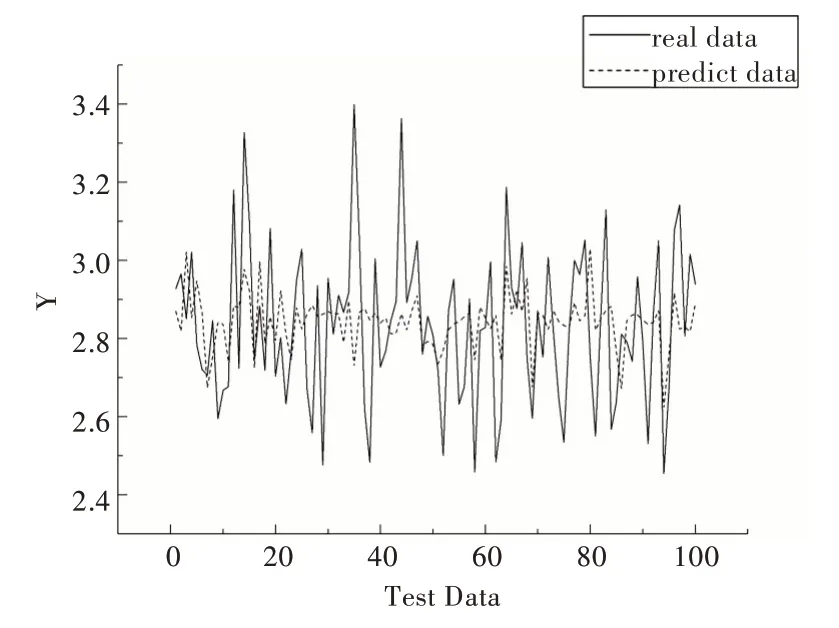
Fig.9 Comparison of PCA-SVR quality prediction results图9 PCA-SVR 实际值与预测值对比
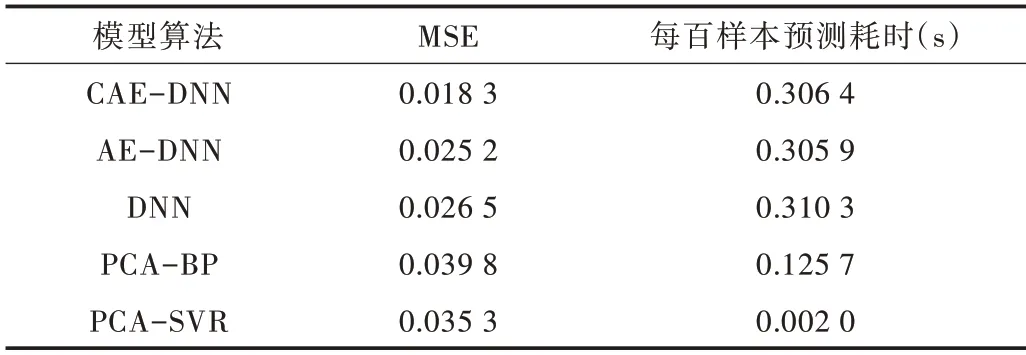
Table 2 Comparison of results of different experimental methods表2 不同实验方法结果比较
通过比较实验得出本文的M1DC-CAE 模型具有以下优点:
(1)CAE-DNN 与AE-DNN 相比,加入正则惩罚项使模型对输入数据在一定程度下的扰动具有不变性,可以减少模型对噪声数据的敏感性,使预测精度提升27.68%。
(2)AE-DNN 与DNN 相比,通过AE 的预训练可以为DNN 提供一个较为合理的初始参数,从而提升预测精度。
(3)与F-CAE-DNN 相比,BN 层、Dropout 和L2 正则化的加入共同改善了CAE-DNN 的过拟合问题,提高了模型的泛化能力。
(4)与PCA-BP 和PCA-SVR 相比,CAE-DNN 特征提取和逻辑推理能力强,更适合处理多工序生产过程质量数据。
结论:本文实验所涉及的质量预测模型中,CAE-DNN的预测精度和性能相对最好,拟合复杂工序过程质量数据非线性程度最高。
4 结语
针对多工序制造数据多特征、多噪声特性,本文提出一种基于CAE-DNN 的多工序产品质量预测方法,并在天池智能制造数据上展开实验。CAE 的预训练为DNN 提供了一个合理的初始化参数,同时抑制了噪声数据,提高了预测精度。经算例验证,相比AE-DNN、DNN、PCA-BP、PCA-SVR 等方法,本文的质量预测模型具有更好的预测精度,对实现生产过程质量的实时预测具有重要意义。但本文方法效率不佳,不适用于实时性要求很高的场合。后续将继续优化神经网络结构,提高神经网络计算效率。

