非恒定流驱动下床面形态变化特征

王 乐,Alan J S Cuthbertson,张尚弘,王永强

(1.华北电力大学水利与水电工程学院,北京 102206；2.School of Science and Engineering,University of Dundee, Dundee DD1 4HN,UK；3.长江科学院水资源综合利用研究所,湖北 武汉 430010)

冲积河流中存在着形态各异、结构复杂的床面形态,如沙垄、交错边滩等,当床面形态出现时,会产生形态阻力,构成对近床面水流结构的扰动,影响泥沙输移的强度及特征[1-3]。实际上,河流系统中的泥沙运动及河床演变主要发生在以洪水为代表的强非恒定流过程中。目前,围绕明渠非恒定流开展的研究主要集中在3个方面。第一,明渠非恒定流水动力学研究,如Graf和Qu[4]以洪水中的水动力要素为关注对象,通过理论及实验方法分析水流参数极值出现的先后顺序；周俊伟等[5]运用量纲分析得到了以微分结构表达的摩阻改进公式。第二,非恒定流作用下泥沙运动特征为主的研究,如刘春晶等[6]的实验表明非恒定流的推移质输沙强度与水流强度变化存在不同步的现象；程小兵等[7]、马爱兴等[8]由实验观测认为非恒定流不存在传统意义上的饱和输沙与平衡输沙,输沙率始终存在滞后现象；吴国茂等[9]分析了Lee等[10]和Bombar等[11]的输沙数据后提出一个综合水沙运动的非恒定性系数来进行拟合；段自豪等[12]分析实验结果得出非恒定流作用下的泥沙颗粒更易起动的结论；Wang等[13]在实验中证实了非恒定流非均匀沙床中不同粒径组间最大输沙强度的滞后性。第三,非恒定流河床演变的研究,如Martin和Jerolmack[14]模拟了流量增加或减小时的河床响应,基于床面形态陡度不变且输沙无绳套特性的矛盾假设建立了床面形态调整时间的预测模型；孙东坡等[15]研究表明黄河下游主槽冲刷总量随含沙量增大而减小,滩地淤积量随含沙量增大而增大；Waters和Curran[16]实验观测到沙波在小洪水事件中形成；Redolfi等[17]用理论模型描述了洪水波中交错边滩随时间的变化特征；赵维阳等[18]分析三峡大坝下游的河床形态时发现,随着来沙量减少,河床呈冲刷态势,洲滩面积也在同步减少。显然,现阶段以非恒定流输沙成果居多，而非恒定流河床演变的研究则只关注某一特定类型的床面形态(如交错边滩)或以河道断面形态为主,真正涉及多尺度洪水过程与多类型床面形态的关联性研究并不多见[19-20]。

鉴于此,本文拟通过水槽实验来生成一系列具有典型代表性的单波非恒定流过程,探究实验动床在不同尺度非恒定流驱动下的床面形态变化特征,定量分析非恒定流洪水尺度与床面形态尺度之间的响应关系,研究成果将为揭示洪水作用下的河床形态变化趋势及河流演变规律奠定基础。

1 非恒定流与床面形态尺度的量化

1.1 非恒定流的定量描述

非恒定性参数(ΓHG)是描述非恒定流的基本参数,是基流与洪峰流间的水深差(ΔH)与洪水总历时(ΔT)的函数,其表达式为

(1)

式中:u*b为基流剪切流速,m/s；ΔT=ΔTR+ΔTF,ΔTR、ΔTF分别为洪水上升段与下降段历时。另外,洪水过程的总水量也会影响到泥沙运动及河床形变。因此,Yen和Lee[21]提出了非恒定流的水流做功概念,其表达式为

(2)

式中:Vol为洪水过程中所包含的总水量,m3,不包括基流量；Hb为基流水深,m；B为水槽宽度,m。此外,Wang[22]用形态参数来判别对称性与非对称性三角形洪水过程,其被定义为洪水上升段和下降段历时的比值,即

(3)

当η=1.0时为对称性洪水过程；当η≠ 1.0时则为非对称性洪水过程。

1.2 床面形态尺度的定量表达

研究非恒定流对床面形态的影响,需要统计分析河床高程数据来确定不同类型的床面形态多维尺度。一般而言,定量描述床面形态大小的参数主要包括波长(λ)、波高(D)以及陡度(ψ)[1]。波长用于表征相邻2个波峰所代表的最大高程点(或2个相邻波谷所代表的最低高程点)之间的水平距离；对应的波高定义为上述2个波峰所指代的空间范围内高程最高点(波峰)与最低点(波谷)之间的垂直间距；陡度为波高与波长的比值,即

(4)

显然,波长、波高是有量纲参量,陡度为量纲一参数,三者被广泛用于描述沙垄等水沙界面普遍存在的床面形态。

2 实验方法介绍

2.1 实验设备及仪器

实验在英国赫瑞瓦特大学水力学实验室的大型水槽内进行。水槽长22 m,宽0.75 m,高0.50 m,断面为矩形,底板为不锈钢,边壁由透明玻璃制成。如图1所示,该水槽为水流循环的封闭系统,坡度可手动调节,水泵设置在水槽入口底端,可输出最大流量为100 l/s,水槽下游出口处布设有可调节的百叶窗尾门。实验中使用的测量仪器包括测试段上下游的电子水位计、超声波流量计、调坡仪及变频器等主要设备。其中,流量由超声波流量计测得,其测量精度可以达到±0.01 l/s。实验用沙分为A、B、C、D 4种,其中,d为沙粒直径。

图1 研究床面形态的水槽实验及主要观测仪器Fig.1 Experimental flume and main equipment employed for studying bed forms developed over a mobile bed

2.2 实验水沙条件

实验水流为典型非恒定流洪水。非恒定流洪水系列分为3个序列,即表1所给出的U1、U2、U3序列,主要考虑不同的形态参数、非恒定性及水流做功对床面形态变化的影响,以实验序列U1为例(见表1),在非恒定流实验组S1a—S1c中,其他参数保持不变,η由0.4增大到2.5；同理,实验组V1a—V1e中只有Wk变化,而在实验组U1a—U1e中ΓHG变化。实验用沙参照了Lee等[10]的实验设计,泥沙粒径范围为1.0～2.8 mm,中值粒径d50=1.95 mm。

表1 实验中的非恒定流条件Table 1 Summary of unsteady flow hydrographs in the present experiment

2.3 实验步骤及河床高程测量

实验前,水槽内铺设厚度均匀的平整沙床(其厚度为11 cm)；实验初期,为使水流能够浸润测试沙床而不造成扰动,将水槽下游的尾门关闭,调控水泵生成最小流量(Q=3.0 l/s),待床面被水流浸没后,打开尾门,缓慢增大水泵输出流量,直至达到基流水平(Q≈17.0 l/s),基流运行约30 min后,使用非恒定流控制系统生成预设洪水过程；非恒定流测试结束后,继续运行基流,并缓慢关闭尾门,以产生回水效应,这样既可保护床面形态，又可增加水深,有利于借助声学多普勒水流仪(Acoustic Doppler Velocimeter,ADV)来测量河床高程,精度可达到±0.1 mm。

3 结果与分析

3.1 非恒定流作用下形成的床面形态

形态参数变化的非恒定流作用下形成的床面形态如图2所示。显然,浅滩或深槽犬牙交替式分布在动床两侧,形成了交错边滩类型为主的床面形态(S1a,S1b)。在3种形态变化的非恒定流洪水作用后,河床高程整体降低,并没有出现局部净淤积(河床高程变化量Δz>0)的情况；冲刷最大深度(≈40 mm)出现在非对称型洪水S1b作用的沙床下游段,与流量梯度差异对最大输沙率的影响有关。具体而言,上升段历时较短的洪水过程涉及的正向流量梯度较大,附加应力增大导致局部河床冲刷更为强烈。

图2 实验序列U1洪水作用下的床面形态与高程变化Fig.2 Detailed bed elevation maps measured for post-hydrograph bed surface in representative tests within experimental series U1

非恒定性变化的洪水过程(U1a,U1c,U1d)对床面形态的影响见图2。随着洪水非恒定性降低,即洪峰流量减小且洪水历时延长,水流对河床的冲刷能力降低,其塑造大尺度床面形态的能力逐渐减弱。相应地,床面形态类型也发生了变化,由较为规则的交错边滩逐渐变为非规则的边滩/沙垄混合的床面形态。图2也呈现了水流做功变化的洪水过程(V1a,V1c,V1d)对床面形态的影响,随着Wk的减小,河床冲刷深度相应减小；同样,对应的床面形态类型也发生了类似变化,由交错边滩逐渐变为较规则的沙垄(如V1d)。

3.2 非恒定流参数对床面形态尺度的影响

实验中各类床面形态的波长、波高、陡度与非恒定流基本参数间的关系详见图3。显然,床面形态的波长并没有随洪水形态变化而表现出明显的趋势性变化,波长维持在1.8～2.8 m范围内；然而,实验观测得到的床面形态波长与ΓHG、Wk表现出一定关联性,具体来说,随着水流的ΓHG增大,波长逐渐减小；随着Wk的增大,波长缓慢增大。相比于形态参数与水流做功,洪水的非恒定性对床面形态波长的影响更为明显。

图3 非恒定流形态、非恒定性及水流做功参数对床面形态波长(平均值+标准偏差)的影响Fig.3 Impact of hydrograph shape,unsteadiness,and total water work on bed-form wavelength (averaged value±standard deviation)

图4所点绘的床面形态波高与非恒定流参数关系表明,随着洪水非恒定性及水流做功的增大,波高也在逐渐增大(图4(b),图4(c))，其中,波高与洪水非恒定性具有显著正相关性。洪水形态与床面形态的波高之间无明显的响应关系。

基于平均波长与波高可得到对应的床面形态的陡度,其与非恒定流参数的关系由图5呈现。显然,床面形态的陡度随着水流非恒定性的增大而增大,两者有显著相关性；陡度随着水流做功的增大而缓慢增大,两者也具有相关性。而在洪水形态变化时,床面形态的陡度并没有呈现趋势性变化,两者之间无明显关联,说明洪水形态对床面形态陡度的影响较微弱。

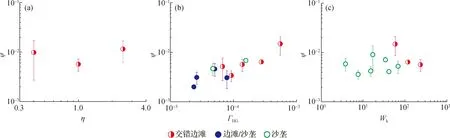
图5 非恒定流形态、非恒定性及水流做功参数对床面形态陡度(平均值+标准偏差)的影响Fig.5 Impact of hydrograph shape,unsteadiness,and total water work on bed-form steepness (averaged value±standard deviation)

值得注意的是,不同尺度洪水作用下,床面形态尺度与类型之间存在着良好的对应关系,当波长与波高变化较小时,床面形态也基本相似,如不同形态洪水影响下形成的交错边滩(图3(a),图4(a))；当波长与波高变化显著时,床面形态类型会发生相应改变,如洪水非恒定性及水流做功变化而驱动形成的交错边滩、沙垄等床面形态,见图3(b)、图3(c)、图4(b)及图4(c)。

图4 非恒定流形态、非恒定性及水流做功参数对床面形态波高(平均值+标准偏差)的影响Fig.4 Impact of hydrograph shape,unsteadiness,and total water work on bed-form height (averaged value±standard deviation)

3.3 非恒定流驱动下床面形态尺度的响应

综上所述,非恒定流基本参数(η,ΓHG,Wk)中,ΓHG与Wk对床面形态的尺度(波长、波高、陡度)有影响,而洪水形态的影响微弱。对于床面形态尺度而言,陡度是一个床面形态的综合描述参数,包含了波长与波高,且陡度是无因次量。因此,有必要重点分析包含有非恒定性与水流做功的非恒定流综合判数与床面形态尺度的综合描述参数(即陡度)之间的关联性,建立表征两者响应关系的定量表达式。

由前文分析知,非恒定性对床面形态尺度影响最大,水流做功的影响次之。基于此,可将2个参数的相对影响用一个综合判数来表示,其形式为

(5)

图6 非恒定流综合参数ΓHGWk0.4与床面形态陡度的关系Fig.6 Relationship between hydrograph combined parameter ΓHGWk0.4 with bed-form steepness ψ

(6)

由拟合关系(6)知,床面形态陡度作为反映床面形态的综合无因次量,其与回归分析得到的非恒定流综合判数紧密关联,拟合线性关系式时,相关系数(R2)达到0.82。当然,式(6)是基于本研究有限实验数据所得,是否适用于更复杂的野外河流形态演变情形,还需要更多实测数据进一步验证。

4 结 论

本文运用非恒定性、水流做功、形态参数来量化多尺度非恒定流洪水过程,研究非恒定流驱动下床面形态演变特征,通过波长、波高及陡度来定量表征床面形态尺度。得到以下主要结论:

(1)在系列洪水作用下实验动床表面分别形成了交错边滩、沙垄及沙垄/边滩相混合的过渡型床面形态,交错边滩常在非恒定性参数与水流做功均较大的洪水作用下形成,而沙垄形成所对应的洪水条件正好相反。

(2)非恒定性参数对床面形态的陡度影响最大,其次是水流做功参数,而洪水形态的影响较为微弱；通过回归分析得到了非恒定流的综合判数,其与床面形态陡度具有良好的关联性,可建立表征非恒定流对床面形态陡度影响的定量描述关系。