莲藕主藕体弯曲破坏离散元仿真分析
焦俊,张国忠,2,杜俊,2,刘浩蓬,2,查显涛,2,邢赫,2
1.华中农业大学工学院,武汉 430070; 2.农业农村部长江中下游农业装备重点实验室,武汉 430070
莲藕(NelumbonuciferaGaertn),简称莲,别名莲菜、荷藕等,是一种用途十分广泛的水生经济作物,也是我国种植面积最大的水生蔬菜[1]。我国莲藕种植主要分布于湖北、江苏、山东、安徽、福建、湖南、浙江等省。近年来,我国莲藕种植区域逐步扩大,种植面积亦呈稳定增长态势。莲藕具有很好的食用和药用价值,莲藕和莲子可供食用,花粉、荷叶、莲芯等也都可以作为菜肴、饮料及保健食品。莲藕地下茎为主要食用部位,其由主藕、支藕组成,无序生长于水下淤泥中,斜植交叉,无规律随机分布。其中,主藕由3~7节膨大节间组成,总长度可达1.2~1.4 m,质量达3.0~4.0 kg[2]。为保证成品合格率,现阶段莲藕采收多用人工挖掘,先由人工脚踏摸索出藕枝大致位置及生长方向,再用手持高压水枪沿莲藕外侧环绕切割、粉碎淤泥,随后人工辅助拔出主体莲藕,使其与淤泥分离[3]。受限于莲藕生长无规律及子藕旁支错综复杂等问题,拔出过程中若部分莲藕枝节仍埋于淤泥中,易发生弯曲、断裂,泥水会经断裂处进入内孔,致使莲藕品质受损。提高效率并减少收获过程对莲藕的损伤与破坏是当前莲藕机械化采收领域亟待解决的技术难题。
采用三维建模以及数值计算仿真软件对采挖作业进行仿真分析,是优化改进机械化收获技术与设备的有效途径[4-6]。莲藕作为一种狭长枝节状的多孔质生物物料,其力学仿真模型缺乏研究。近年来,有关农业物料力学特性的研究如肥料、马铃薯[7]、三七种子等散粒以及茎秆类农业物料的离散元建模和仿真参数标定的报道逐渐增多。于庆旭等[8]采用逆向工程技术对三七种子进行了三维建模,通过碰撞试验、斜面试验、圆筒提升堆积试验标定其接触参数,并开展非规则散粒物料的仿真模拟。马文鹏等[9]以苜蓿种子休止角与堆积角开展双指标多目标寻优计算得到其离散元接触参数,并通过槽轮式排种器进行试验验证。张涛等[10]采用抽板试验测定了玉米秸秆径向堆积角,以其为目标采用正交试验标定了接触参数。廖宜涛等[11]以不同直径的饲料油菜薹期收获茎秆为对象,结合圆筒提升堆积试验以及弯曲破坏仿真试验分别标定其接触参数以及粘结参数,建立茎秆的离散元力学模型。
本研究以鄂莲5号莲藕为对象,采用物理试验测定其主藕体本征参数、接触参数以及内孔尺寸,利用三维反求技术获取主藕体轮廓以及放样切割内孔方法完成主藕体三维建模,采用EDEM内置的Hertz-Mindlin with bonding粘结模型建立主藕体离散元模型,进而开展弯曲破坏规律仿真分析,以期为莲藕机械化收获过程仿真研究以及莲藕损伤、破坏途径与因素的分析提供参考。
1 材料与方法
1.1 试验材料
试验材料为湖北省广泛种植的莲藕(NelumbonuciferaGaertn)鄂莲5号。选取第二节主藕体为对象进行仿真分析,取样区域与部位如图1所示。

图1 莲藕取样区域Fig.1 Sampling diagram of lotus root
1.2 本征参数测量
1)轴向压缩试验。为测定主藕体弹性模量、剪切模量、泊松比等本征参数,选取莲藕表层和心部等部位制作5 mm×5 mm×5 mm立方形标准试样,在TMS-Pro质构仪进行平板轴压缩试验(图2)。设置压缩速度为10 mm/min、加载位移为4 mm,重复10次,通过测量试样单轴压缩前后高度与直径变化量并参考文献[12]方法计算获得主藕体弹性模量、剪切模量、泊松比等本征参数。

图2 单轴压缩试验Fig.2 Uniaxial compression test
2)主藕体-钢摩擦系数测定[10]。采用斜面法获取主藕体-钢摩擦系数。试验前根据前期莲藕外形尺寸抽样调查结果,选取横截面长轴为(70±5) mm、短轴为(60±5) mm的第二节莲藕,去除两端,选取中间部位制备成长100 mm筒状主藕体试样。静摩擦系数测量时,为保证试样在斜面上仅能产生滑动,将2节主藕体沿垂直纵轴方向插入直径5 mm、长20 mm钢条,形成并联结构摆放(图3A),缓慢推动斜面至其发生滑动,记录该时刻斜面与水平面夹角,重复20次取平均值,计算得到主藕体-钢静摩擦系数。测量主藕体-钢滚动摩擦系数时(图3B),取1节试样沿轴向方向放置于斜面上,按照静摩擦试验方法试验,试验同样重复20次,最后取平均值计算滚动摩擦系数。

A:滑动试验 Coefficient of static friction test; B:滚动试验 Coefficient of rolling friction test.
3)主藕体-主藕体摩擦系数测定。目前尚无对主藕体间摩擦系数测量的文献报道。本研究参照GB/T 10006―2021《塑料 薄膜和薄片 摩擦系数的测定》标准,采用摩擦系数测试仪进行测量。测量时,沿主藕体周向均匀切取若干个规格为8 cm×20 cm×1 cm切片,并采用粘结剂将切片内表面均匀依次密布粘在滑块以及试验台上,使其外表面相对所采用粘结剂对主藕体外表面无渗透硬化作用(图4)。粘贴完毕后,驱动滑块以100 mm/min的速度相对试验台直线运动,牵引方向与摩擦方向平行,以模拟主藕体间滑动、滚动等相对运动情形,测量计算主藕体间滚动摩擦、静摩擦系数。试验时控制试验时间,确保试验环境条件恒温恒湿,保持主藕体以及切片水分恒定,试验前后采集同一部位小块主藕体试样,采用水分测定仪测定其含水率,均稳定保持在75%±5%。

图4 主藕体-主藕体摩擦系数测定Fig.4 Measurement of friction coefficient between main lotus root and main lotus root
4)主藕体碰撞系数测定。为测定主藕体-钢碰撞恢复系数,制备与前述摩擦试验规格一致主藕体试样,在其表面涂上粉末以用于标记碰撞点。基于压缩试验结果以及防止试验时损伤主藕体,调整台架高度H为 20 cm(图5)。试验时主藕体莲藕在高度H处经限位环投放,自由落体至与碰撞板发生碰撞后做抛物线运动落入沙箱。同一试样多次重复试验后取其集中落点并采集落点距碰撞点水平距离S1,以及无底座时主藕体落入沙盘的水平距离S2,按照式(1)计算碰撞后水平、垂直方向分解速度vx、vy,按照式(2)计算主藕体-钢碰撞恢复系数[13]。
(1)
(2)

图5 碰撞模型Fig.5 Model of collision
为测定主藕体间碰撞恢复系数,开展主藕体间对心碰撞试验。试验时,在纵轴高度20 cm处释放主藕体,其与下方固定状态主藕体试样碰撞,以下方主藕体试样上表面轴向切线方向为横轴,垂直方向为纵轴,建立如图6所示坐标系,采用高速摄影仪记录上方主藕体碰撞后沿纵向弹跳高度,计算二者比值得到主藕体间碰撞恢复系数[14]。

图6 主藕体对心碰撞试验Fig.6 Central collision test between mainlotus root and other main lotus root
5)主藕体本征与接触参数。经以上试验得到主藕体本征与接触参数,结果如表1所示。
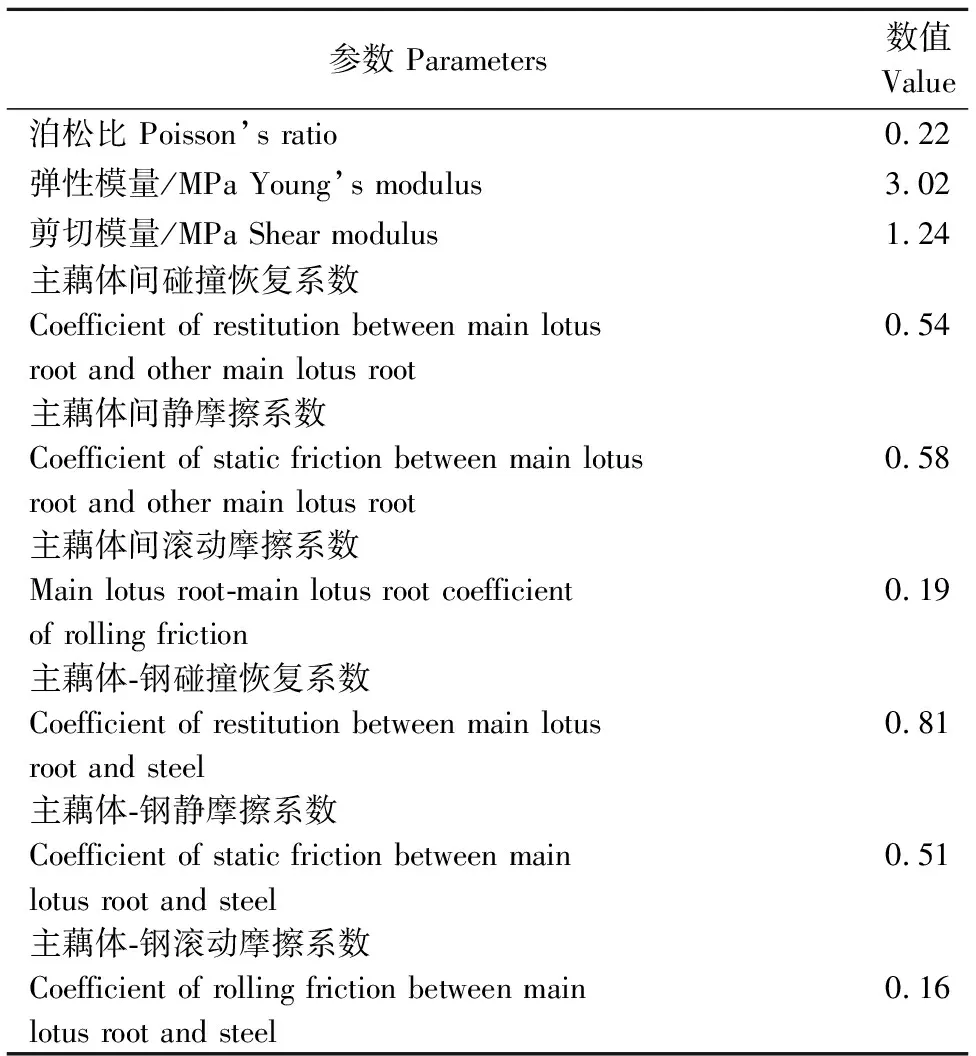
表1 主藕体本征与接触参数 Table 1 Intrinsicand contact parameters of main lotus root
1.3 主藕体仿真模型建立
1)三维模型获取。主藕体结构不规则,其形状参数直接影响粘结模型中粘结键数量以及粘结结构。为此,采用逆向工程技术,通过EinScan-pro手持式3D扫描仪对其扫描,封装点云数据,从而得到精确主藕体轮廓模型[7]。采用Geomagicstudio 3D软件,将点云数据转换为多边形,删除尖状物、填充孔,去除多余特征,针对反映主藕形状特征的轮廓锐化处理,生成栅格,拟合曲面得到主藕NURBS轮廓曲面模型。由于主藕体内部存在贯通内孔(图7),其多孔质结构直接影响物料机械强度,故将主藕体内孔依次标号后统计测量分析其形状参数(表2),导入Solidworks三维软件,放样切割得到主藕体三维实体模型。

图7 主藕体截面Fig.7 Cross section of main lotus root

表2 主藕体内孔尺寸 Table 2 Size of inner hole of main lotus root mm
取颗粒半径3 mm,以外表面轮廓向内缩放2倍颗粒半径距离建立壁面,将主藕体模型分为内外两层,用于后续建立外表皮以及心部的颗粒材料(图8)。
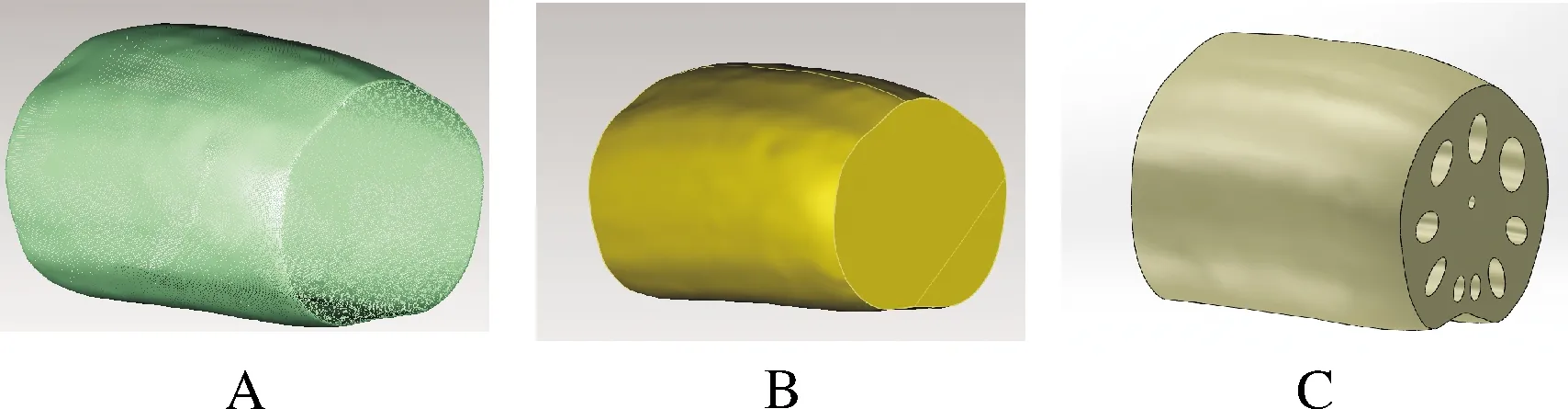
A:点云数据 Point cloud data; B:轮廓曲面模型 Profile surface; C:实体模型 Solid model.
2)颗粒填充与粘结。将主藕体颗粒模型分为心部与外表皮颗粒模型。如图9A所示,外表皮模型利用Workbench构建单层Prism网格模型后导入Fluent中,利用udf计算得到空心六边形密排面(图9B),构建双层prism网格模型后分别导出内外表面以及整体节点坐标信息,筛选去除重复坐标信息后得到中层节点信息,将其作为正六边形中心,最终得到完整密布形外表皮颗粒模型,后处理输出外表皮XML文件[15]。
设置壁面模型为Hertz-Mindlin无摩擦(no slip)模型,采用落雨法生成心部颗粒,设置box为physical,作为颗粒工厂生成心部颗粒后,利用平板向下压缩,保证颗粒密实堆积,而后主藕体内层几何模型由初始Virtual状态变为physical状态,沿壁面外形束缚颗粒。压缩过程中存在部分颗粒进入内孔,设置内孔模型以100 mm/s速率沿轴向直线运动,同时设置接触几何与多余颗粒接触,采用Remove particle API,清理内孔中多余颗粒,后处理输出心部XML文件。提取2份XML文件中心部与外表皮颗粒坐标信息,输入XML文件中得到完整填充文件,将完整填充文件输入EDEM。
若壁面弹性模量过大,会造成颗粒间短时间难以达到平衡状态,而过小也会造成颗粒在加载压实过程中穿透壁面使得颗粒无法贴合非球形壁面。为获取反映莲藕形状特征的精准粘结模型,取壁面弹性模量为颗粒弹性模量的1/10,在颗粒间无明显重叠下重新排列填充直至达到平衡状态,最终得到主藕体颗粒模型(图9C)。

A:网格模型 Mesh model; B:六边形基础模型 Hexagon base mode; C:完整模型 Complete model.
1.4 主藕体弯曲破坏离散元仿真
1)主藕体弯曲破坏试验。如图10A所示,采用TMS-Pro质构仪(FTC公司)进行主藕体弯曲破坏试验,选用质构仪自带长(A)×宽(B)×高(H)×厚(R,刃口)为50 mm×10 mm×60 mm×3 mm刀头(图10B),以10 mm/min速率对主藕体施加载荷,记录加载过程中随加载位移变化的弯曲破坏力曲线,试验规格与前述摩擦试验一致,固定支撑两点间距为50 mm,参照文献[11]重复试验10次,统计显示最大破坏力平均值为315 N。由图10C可知:(1)起始时,主藕体在加载过程中经过原点到A间为塑性形变阶段,此时局部出现由斜裂纹扩展导致的剪切破坏以及轴向拉裂纹扩展而出现的劈裂破坏[15];(2)随后,在A-B阶段出现应力集中现象,裂纹扩展迅速,对外表现为局部脆性断裂;(3)而后,在B-C阶段主藕体开始断裂,裂纹扩张至藕心部,应力增加;(4)最后,压头继续加载,藕体迅速断裂,表现为典型楔入断裂。

A:弯曲破坏试验 Bending failure test; B:弯曲刀头示意图 Curved tool head; C:典型主藕体弯曲破坏应力-应变曲线 Typical bending failure curve of main lotus root.
2)粘结模型及参数计算。弯曲破坏试验显示主藕体产生劈裂现象,故视其为脆性材料。由于Hertz-Mindlin with bonding模型是1个粘结接触模型,常用于模拟断裂问题,故用其来模拟主藕体弯曲破坏过程[17]。Hertz-Mindlin with Bonding模型中颗粒间力学特性满足梁弹性理论[18],如式(3)所示:
(3)
其中,Kn、Ks分别为法向接触刚度、切向接触刚度,N/m;Fn为法向应力,成对颗粒接触后产生切向应力增量ΔFs叠加在切向应力Fs上[19]。颗粒间受力以式(4)随时间步长迭代计算得到[20]:
(4)

离散元模型需要标定的参数:法向粘结刚度kn,N/m3;切向粘结刚度ks,N/m3;切向临界应力τmax,MPa;法向临界应力σmax,MPa;粘结半径R,m。为节约仿真计算时间,球形颗粒物理半径r为3 mm,接触半径取4 mm,粘结半径一般为接触半径的1.2~2.0倍,粘结半径R取5 mm[21]。根据梁理论,计算得到粘结键之间的法向临界应力和切向临界应力:
(5)
式(5)中,当拉伸应力、剪切应力超过上述最大值后,粘结键断裂。
3)主藕体弯曲破坏离散元仿真单因素试验。按照前述测定的结果,开展主藕体弯曲破坏仿真试验(图11)。由于Hertz-Mindlin with bonding模型中法向粘结刚度、切向粘结刚度、法向临界应力、切向临界应力的粘结参数均对仿真结果存在影响,为探索其影响规律,设置外表皮、心部、外表皮粘结参数一致,采集初始段曲线,对法向粘结刚度x1、切向粘结刚度x2、法向临界应力x3、切向临界应力x4,分别设置106、107、1083个水平(表3),重复10次,开展主藕体弯曲破坏仿真单因素试验[22]。

图11 主藕体弯曲破坏仿真试验Fig.11 Bending failure simulation of main lotus root
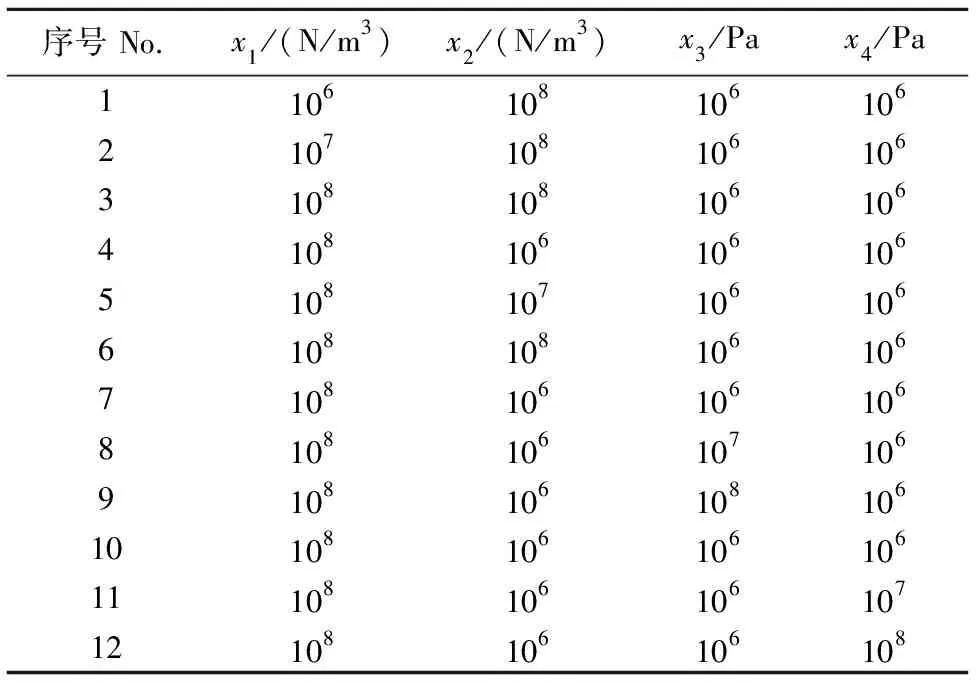
表3 单因素试验 Table 3 Single factor test
试验时,设置颗粒接触模型为Hertz-Mindlin with bonding模型,在外表皮颗粒、心部颗粒以及外表皮-心部颗粒间分别添加粘结键,输入粘结参数,设置几何壁面弹性模量为7.94×1010MPa,基于该模型对时间步长敏感,取低于10%时间步长,取整后为3×10-5s进行运算。
由图12可知,法向、切向粘结刚度对曲线位移值以及第一峰值影响显著,法向临界应力、切向临界应力对曲线峰值以及位移值影响不显著。根据单因素试验获得法向粘结刚度、切向粘结刚度、法向临界应力、切向临界应力参数上下限区间如表4所示。

表4 粘结参数编码 Table 4 The code of bonding parameter
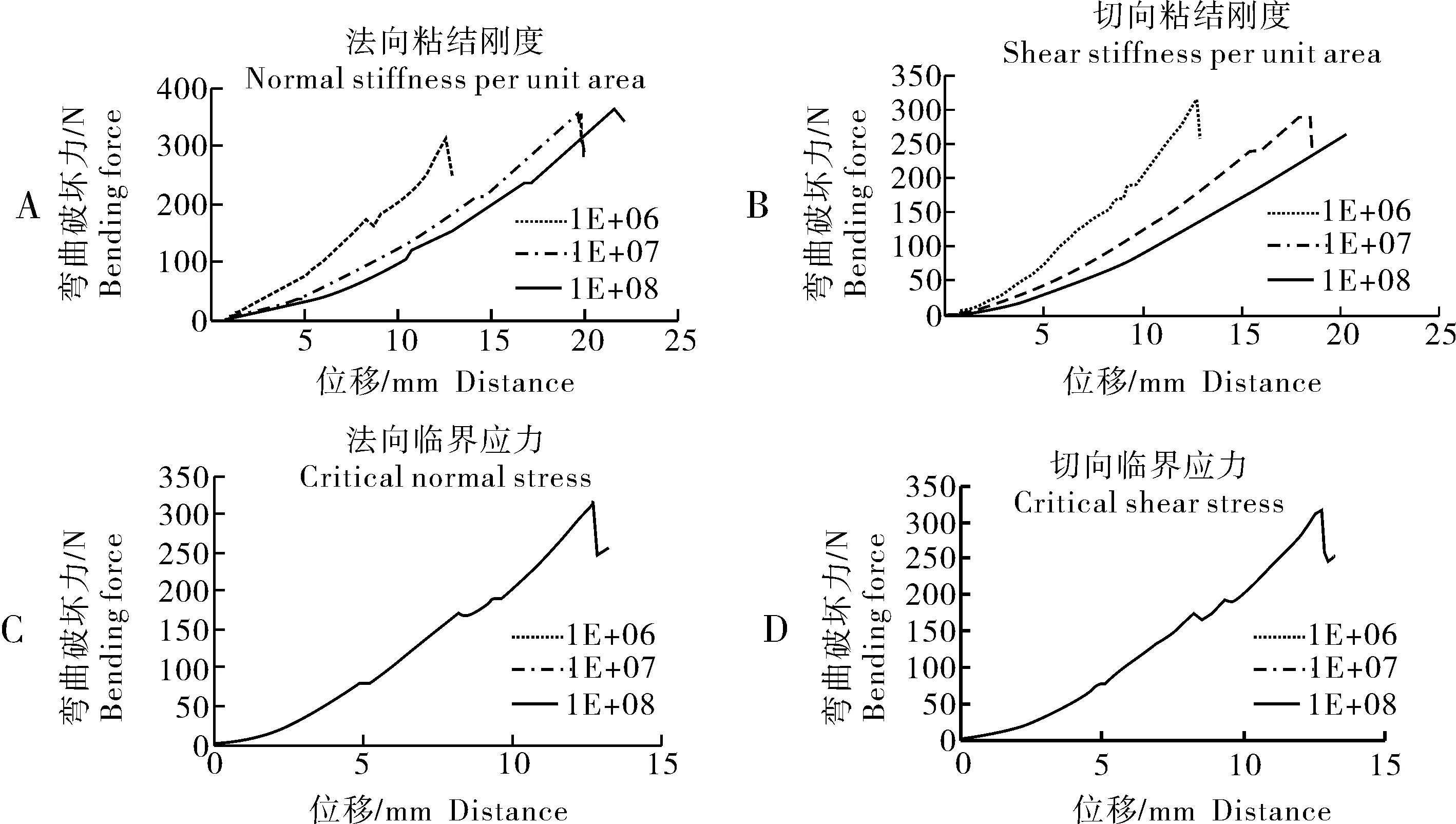
图12 单因素试验Fig.12 Single factor test
4)主藕体弯曲破坏离散元仿真二因子试验。根据单因素试验结果,为进一步获取上述因素对弯曲破坏曲线的影响规律以及二次效应(弯曲性)是否显著[23],开展了5个中心点的二水平因子试验。
5)最速下降法。为快速趋近实际弯曲破坏曲线及关键破坏点,从二因子试验获取的一阶响应曲面方程中心点出发,取沿垂直于拟合曲面等高线的直线为最速下降路径,取步长与回归系数成正比,按照最速下降法寻找法向粘结刚度、切向粘结刚度、法向临界应力、切向临界应力的最优解。
2 结果与分析
2.1 一阶响应曲面分析
由单因素试验可知,刚度参数同时对曲线第一峰值以及位移值影响显著,为精确衡量仿真曲线与实测曲线相似性,采用式(6)以仿真以及实测曲线中第一峰值与位移点组成的坐标点,计算坐标间欧拉距离(ED)作为衡量仿真与实测试验相对误差的指标。
(6)
式(6)中,Sa、Sb分别为仿真、实测曲线坐标点,Fa、Fb分别为仿真、实测曲线第一峰值,Da、Db分别为仿真、实测曲线位移值。
试验指标包含峰值以及位移点,两者度量单位不一,需采用式(7)所示的阙值比较法进行无量纲化处理。
(7)
由式(6)和式(7)可得无量纲化的欧拉距离ED0。
(8)
以表4所示参数上下限数值设计二水平因子试验(表5)。由表6可知:主效应x1、x2对ED0参数影响显著(P<0.01),主效应x3、x4、弯曲性(纯二次效应)以及其余交互作用均对ED0参数影响不显著(P>0.05),弯曲性不显著证明一阶响应曲面方程具有适合性。使用最小二乘法,利用规范变量以一阶模型拟合得到关于ED0参数一阶响应曲面方程:
ED0=2.24-7.20×10-9x1-1.06×10-8x2+ 3.75×10-17x1x2
(9)

表5 二水平因子试验 Table 5 Regular two-level factorial design

表6 一阶曲面响应模型方差分析 Table 6 Analysis of variance of first order surface response equation
2.2 最速下降法分析
由一阶响应曲面方程可知,x1、x2对ED0参数为负效应。非显著项x3、x4取中间水平。以一阶响应曲面方程中系数最大的x2作为基准值,取0.70 MPa为基本步长,由式(10)所示规范向量x1、x2与自然向量z1、z2关系,设计最速下降试验(表7)。
(10)

表7 最速下降试验 Table 7 Steepest ascent
由表7可知,在步长为原点+3Δ处ED0参数最低,该粘结参数下第一弯曲峰值为269.72 N、位移值为7.14 mm,与实测试验数据相对误差分别为2.56%、2.00%,总体误差为2.28%,可以认为此时法向粘结刚度、切向粘结刚度、法向临界应力、切向临界应力等粘结参数为最优解,仿真与实测弯曲曲线对比如图13所示。
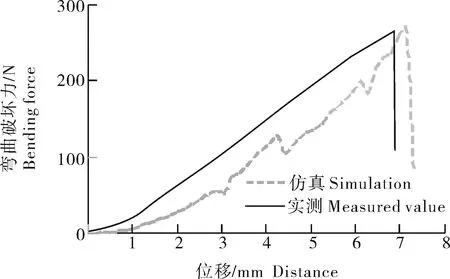
图13 仿真-实测曲线Fig.13 Curve of simulation-test
3 讨 论
本研究建立了鄂莲5号主藕体离散元模型,使用Hertz-Mindlin with bonding模型对其弯曲破坏模型进行了仿真分析,采用单因素试验、二因子试验、最速下降法得到法向粘结刚度为5.814×108N/m3、切向粘结刚度为3.450×108N/m3、法向临界应力为3.80 MPa、切向临界应力为3.12 MPa。第一弯曲峰值269.72 N、位移7.14 mm,相较实测曲线相差2.56%、2.00%。 对仿真模型各关键参数分析显示,法向刚度粘结系数与切向粘结刚度对于第一弯曲力峰值以及峰值位移点影响显著,而法向临界应力与切向临界应力对第一峰值以及位移点影响不显著,其中法向刚度大于切向刚度,第一弯曲力峰值大于第二弯曲力峰值。
本研究仅对主藕体弯曲破坏塑形变形阶段进行了仿真模拟分析,后期需要进一步对藕节以及主藕、藕节联合体的受力破坏进行研究。此外,本研究未分析截面藕孔分布以及对藕体破坏性能的影响,后续也需进一步开展研究。

