基于网格空间规划的配电网时空负荷自动预测计算方法

朱 力，李 成，肖 康，刘云鹏

（1.国网襄阳电力公司，襄阳 441000；2.武汉飞脉科技有限责任公司，武汉 430070）

0 引言

现阶段的配电网具有智能化特征，通过集成传感技术、通信技术、存储技术等智能化操作方式调控电力资源，按照不同用电特征，满足不同用电类型的日常需求。但居住用电、商业用电以及工业和农业用电等，由于在社会环境中的分工不同，所以对于电力资源的需求存在明显的差异性，加上不同用户面对的社会大环境也不一致，在复杂用电方式、不同用电量的影响下，配电网的日常工作面临着较大困难，配电网的时空负荷序列，逐渐呈现出不规则、无规律的变化趋势，影响配电网的正常工作。而配电网自身在自然环境和自身因素的影响下，也容易出现故障而产生异常时空负荷，影响整体电力资源分配工作[1]。综合考量上述可能存在的问题，研究能够预测配电网时空负荷的方法。

现有的配电网时空负荷自动预测计算方法，对于内部环境因素与外部环境因素考虑的不够充分，在固定的预测周期内，获得的数据存在缺失、遗漏、重复等问题，影响对真实负荷分布状态的预测，在预测负荷的时间属性与空间范围时，难免会出现数据偏移的现象，本次研究引入网格空间规划理念。网格空间规划不仅仅是简单的区域划分，该理念是在充分考虑环境因素的基础上，结合外部因素的影响程度，对不同的数据进行空间位置划分，得到不同类型的划分结果，是一种精细化的区间划分方法，对于解决该问题有较好的应用前景。下面针对网格空间规划，提出全新的配电网时空负荷自动预测计算方法。

1 配电网时空负荷自动预测计算方法

1.1 提取负荷的时间属性

负荷是对负荷功率变化规律的简单描述，通过负荷的时间特性在不同周期的时间尺度上体现。研究针对负荷时间属性的基本特征，采用核密度优选法完成提取，获得不同损耗选的特征规律。该方法假设负荷为随机变量u，随机变量在定义域[x，y]中的T个样本，用序列u1，u2，…，uT表示。设置f（u）为参数u的概率密度函数，则该计算公式为：

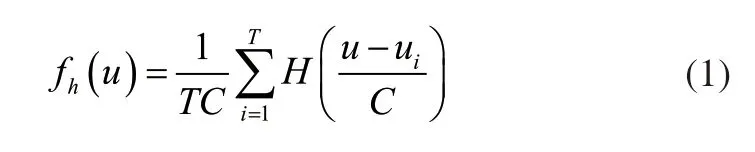
式(1)中：C表示带宽；H表示核函数；ui∈ uT，表示第i个随机变量[2]。由于该函数需要具备连续性特征，所以将单峰平滑概率密度函数作为高斯核函数，计算公式为：

上述公式中的γ＞0，表示一个常数值。通过上述过程第一步确定光滑性较好的核函数。设置样本数据标准差优化核函数的自适应性，得到：

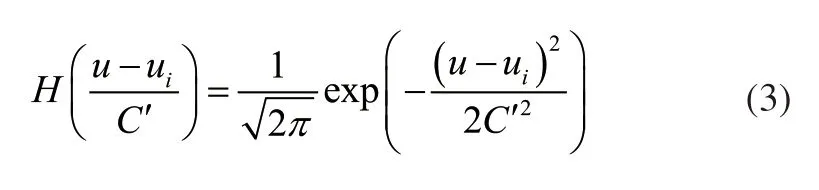
式(3)中：C'表示调整后的带宽。此时将式(3)的结果代入式(1)，得到新的概率密度函数为：

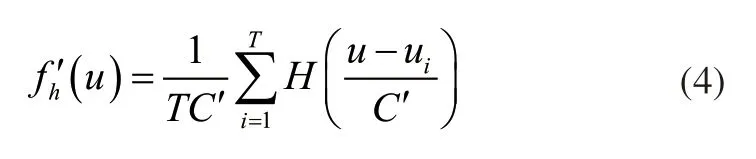
完成上述步骤后，以核密度估计的计算结果为依据，利用MATLAB软件处理T个类型不同的样本，针对其中概率密度最大的样本，以约束检验的方式完成数据分析，当检验结果具有预期的代表性特征时，则输出该数据，完成负荷的时间属性提取工作。若检验结果不具有代表性，则设置一个能够存放样本的矩阵，用EC（a，b）表示，其中a与b分别表示行和列。利用该矩阵在同一周期内，采集多个较为近似的负荷样本值，将其中相对能代表特性的数据作为综合代表性数据。获取样本中的异常数据类型并修正，然后再次进行判断，将概率密度最大的样本，作为同属性样本的代表。直接输出具备代表性的样本，得到负荷的时间属性。

1.2 提取负荷的空间属性

将配电网负荷看作集中分布在线路末端的数据，利用相邻的两个测量点之间的电位差的纵分量，描述电压损失值。采用负荷距离的方式近似描述供电半径，则负荷供电半径与电压电流之间的关系，可以通过下列公式计算获得：

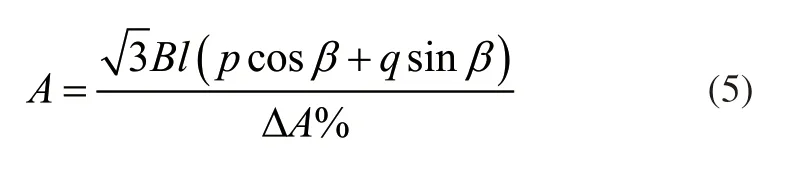
式(5)中：A表示配电网的额定电压；B表示流过配电网线路的电流；l表示不同空间内的线路实际长度；p和q表示电阻和电抗；β表示功率因数；△A表示电压动态变化比例[3]。已知配电网的横截面积、几何间距会影响电阻和电抗，则调整上述公式，得到负荷的分布形式：

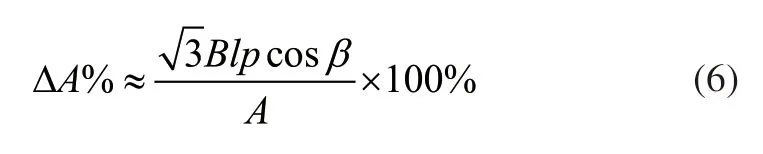
根据负荷的分布形式提取三相不平衡特性，这一过程中假设相电流、三相不平衡度分别为BD和Dφ，三相电流的均值为BD，则三组参数的计算结果为：

式(7)中：相存在D=1，2，3的条件，与B1，B2，B3对应。由于BD，max=3、BD，min=0，所以设置φD,max=2，φD,min=-1。根据不平衡度概念可知φ1+φ2+φ3=0，则其中3相电流的提取结果为：

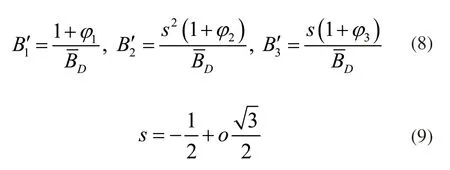
式中：s表示相的约束条件；o表示电压层末端负荷[4]。通过上述计算过程，完成配电网负荷空间属性的提取工作。

1.3 多级聚类自动规划网格空间

根据配电网时空负荷时间与空间属性特征的提取结果汇总电力信息，构建电力负荷集合，利用K-means聚类算法多级聚类时空负荷。该算法假设电力负荷集合中，共存在X个时空负荷数据样本，利用X=（X1，X2，…，Xn）描述集合中的n个对象。K-means算法初始化k个聚类中心，用Z1，Z2，…，Zk表示，存在1≤k≤n。根据上述设置准备数据，计算聚类中心与样本之间的实际距离，公式为：

式(10)中：d表示属性维度；Xi表示集合中的第i个样本；Zj表示第j个聚类中心；Xit、Zjt表示第t个属性。其中1≤i≤n、1≤j≤k、1≤t≤d。按照顺序计算每个聚类中心与样本之间的距离，得到k个群簇，用R1，R2，…，Rk表示。此时根据上述公式计算内部因素影响下的距离；当计算存在外部影响因素时，引入影响因素权重系数iω，根据式(10)得到能够满足外部影响因素干扰的新的欧式距离公式：

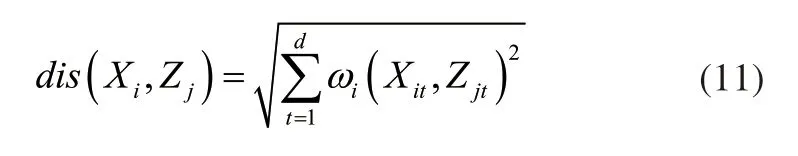
K-means算法选择第一个特征向量，将数据聚在空间相近或者是空间功能相近的类的集合当中，按照上述过程得到一级聚类结果[5]。一级聚类完毕后选择第二个特征向量，按照同样的过程得到二级聚类结果。以此类推，通过选择不同数量的特征向量，完成不同级数的聚类，根据多级聚类自动规划网格空间，实现对不同配电网服务区域的分割。

1.4 概率模型计算用电调整预测区间

假设各个用电区域的行为是相互独立的，那么根据区域参数和需求行为，构建概率模型计算用电需求。按照城市空间结构提取用电类型，包括居民用电、商业用电、工业用电、农业用电以及其他用电。假设所有用电行为服从泊松分布，则用电概率为：

式(12)中：r表示范围限制参数；θ表示固定常数；μr表示泊松分布参数。假设Wa，b、Ia，b表示用电区域和用电时段，则计算公式为：

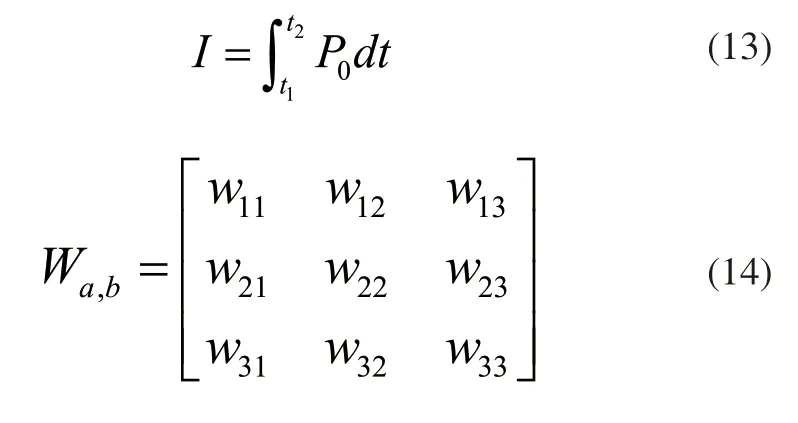
公式中：t表示时间；w表示位置坐标[6]。已知用电需求之间不具有相关性，所有用电均为独立行为，所以根据蒙特卡洛随机抽样理论，根据式(12)～式(14)构建配电网的配电概率模型，公式为：

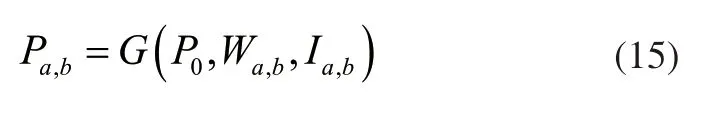
式(15)中：Pa，b表示位置在第a行第b列的配电概率计算结果。根据上述计算结果，调整网格空间的规划区间范围，实现基于网格空间规划的配电网时空负荷自动预测计算方法。

2 预测与分析

2.1 设置预测结果评价指标

2.1.1 点预测精度评价指标

针对预测区域内的所有预测节点，采用绝对百分比误差指标（APE）和平均绝对百分比误差指标（MAPE），评价单个节点负荷预测精度。两个指标的一般计算表达式为：

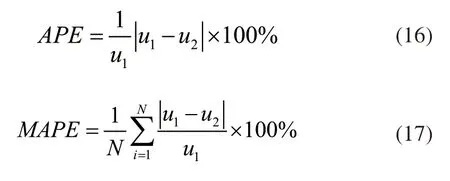
公式中：u1表示负荷的真实值；u2表示负荷的预测值；N表示负荷预测值的数量。根据上述两组公式，评价点预测精度。

2.1.2 区间预测精度评价指标

在点预测精度评价的基础上，评价整个区间的预测精度，为了保证评价结果具有说服力度，采用预测区间覆盖概率指标（PICP）、预测区间归一化平均宽度指标（PINAW）、覆盖密度指标（CDI）评价区间预测精度。其中第一类指标评价实际值落在预测区间内的概率，第二类指标调整区间宽度，第三类指标衡量对预测区间的覆盖程度。三组指标的计算公式为：

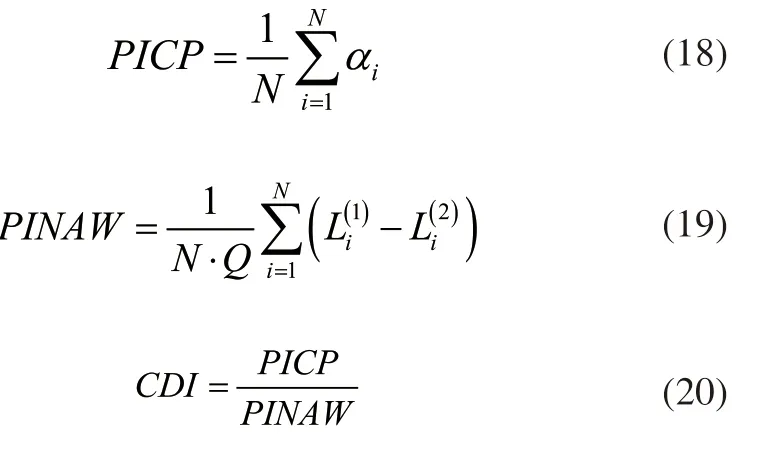
式中：ai表示评价第i个预测区间对实际值的覆盖程度指标；Q表示实际值最大值与最小值之间的差值；表示第i个区间的预测上限、下限条件。假设目标i为vi，当目标位于之间时，存在条件ai=1；若vi不在限制范围之内，则存在条件ai=0。所以PICP指标和CDI指标的计算结果越大，越能说明预测区间的覆盖程度和覆盖密度越高。根据上述计算两组计算公式获得不同的评价指标，根据指标衡量预测方法的应用效果。

2.2 区域配电网年度用电时空负荷分布预测

2.2.1 区域介绍

以某一城市区域作为算例，预测该区域配电网年度用电时空负荷分布情况。该区域共有12条主干道路、2个交通中心、24个主要公共建筑。走访当地的电力企业，获取该区域的配电网电力时空负荷分布数据，样本数据时间为2019年，并调查该区域这三年期间的人口总数、平均气温以及GDP指数。已知预测过程中影响时空负荷分布预测效果的因素存在内部与外部两个因素，所以在开始预测前，为了将可能产生的影响降至最低值，利用曲面插值拟合的方法，根据建筑类型与主干道路之间的距离，绘制一个趋势图，如图1所示。

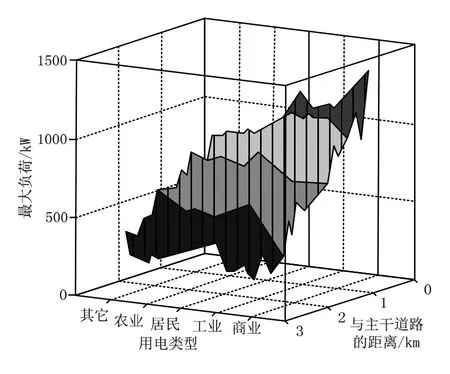
图1 建筑类型与主干道路距离变化趋势

图中x轴描述不同的建筑类型；y轴描述建筑与主干道路之间的距离；z轴描述不同年份的最大用电负荷。根据该变化趋势可知，商业和工业建筑的用电需求最大，且距离主干道路越近，需要的电量也越大。

2.2.2 网格空间规划

根据已知数据和图1，本文提出的预测计算方法多级聚类时空负荷，该过程如图2所示。

图2 多级聚类过程

本文方法根据不同的负荷时空属性进行多级聚类，得到上述多级聚类结果。其中图2(a)根据时空负荷的位置敏感度，将数据聚为4类；图2(b)是根据负荷的时空类型，将数据聚7类；图2(c)是根据图2的趋势变化情况，将数据聚为11类。根据上述聚类过程，本文方法进行网格空间规划，得到图3所示的网格空间规划结果。

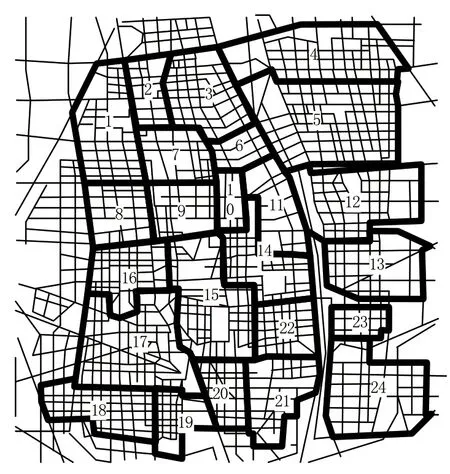
图3 网格空间规划结果

根据上述规划结果可知，按照不同的用电空间负荷。将24个用电建筑划分为不同的用电网格区间，每个区间都代表了不同的配电网时空负荷总量。

2.3 预测结果评价

2.3.1 点预测精度评价

结合式(16)和式(17)的点预测精度评价指标，评价图3所示的区间负荷预测结果，如图4所示。

根据图4可知，当平均绝对百分比误差指标MAPE的值在2%～6%时，多级聚类选择的时空负荷比例最大，超过了40%；当MAPE的值超过6%，多级聚类选择的时空负荷比例约为2%，说明多级聚类结果是可信的，说明图3的预测点具有较高的精度。

图4 时空负荷预测点评价

2.3.2 区间预测精度评价

根据上述结果随机提取4个区域的人口总数、平均气温以及GDP指数真实值。根据本文构建的概率模型，得到负荷属性集合U和网格空间规划的概率值P，其中第一组中：Xpop和Ppop的值为919.05和0.0345；Xtem和Ptem的值为17.41和0.0345；XGDP和PGDP的值为6729.52和0.0345。第二组中：Xpop和Ppop的值为925.77和0.4518；Xtem和Ptem的值为17.53和0.4518；XGDP和PGDP的值为6782.48和0.4518。第三组中：Xpop和Ppop的值为932.52和0.0345；Xtem和Ptem的值为17.68和0.0345；XGDP和PGDP的值为6835.62和0.0345。根据三组结果得到95%、97%以及99%三个置信度，结合式(18)～式(20)的指标，评价置信度为95%、97%、99%时的区间预测精度，结果如表1所示。

根据表1的评价结果可知，随着置信度的增加，PICP指标的计算结果不断增大，说明预测区间的覆盖度随着预测结果可靠性变化而变化，这是实验测试人员想要看到的结果。根据PINAW指标的计算结果可知，置信度的增加同样影响了预测区间宽度，说明PICP指标的提高是以增大区间宽度为代价的。所以根据CDI指标选择预测区间宽度，发现当置信度为95%、97%以及99%时，CDI的值均超过了1.5，预测范围根据真实数据自动变化，证明了本文研究的预测方法具有自动计算功能。

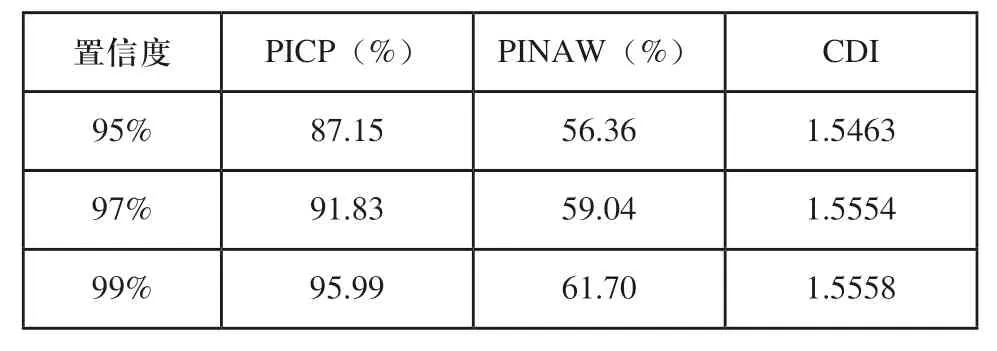
表1 区间预测精度评价结果

3 结语

研究以传统时空负荷自动预测计算方法为参考，利用网格空间划分的方法提高了预测精度，为配电网的电力调度工作提供可靠的数据来源。但此次研究没有将提出的方法与多组传统方法进行对照，今后在时间与资金条件都允许的条件下，可以展开对照实验，根据不同方法之间的预测差异，进一步优化本文的预测方法，为用电负荷管理工作提供更可靠的技术支持。