微型晶体谐振器激光调频作动平台的探针末端定位误差分析

吴彦霖,李刚炎,方 豹

(武汉理工大学 机电工程学院，湖北 武汉 430070)

微型晶体谐振器的主要作用是在电子产品中提供时钟频率。近年来，随着5G技术的发展，市场对于尺寸更小、频率更高、稳定性好的微型晶体谐振器的需求量大增[1-2]。微型晶体谐振器的谐振频率在出厂前需要进行微调，使之达到需要的标称值，这是保证品控的关键工艺。激光调频技术是将传统的激光打标技术应用于微型晶体谐振器的减薄调频中，与传统的镀膜调频法和离子束真空减薄法等加工技术相比，具有清洁、精度高、灵活高效等优点，更适于大规模现代化生产。微型晶体谐振器激光调频作动平台的探针末端与微型晶体谐振器电路部分直接接触，并与起振条构成调频回路，接触点的定位精度直接影响产品的调频质量[3]。因此，为提高激光调频作动平台的调频精度，更好地进行品控，必须建立探针末端定位误差模型，分析各主要参数对误差的影响，以降低损耗，提高误差补偿效率。

国内外学者在几何误差建模方面进行了深入研究，提出了多种空间模型的建立方法[4-7]，其中，多体系统理论考虑各零部件所产生的误差因素和耦合关系，可以从整体精度反推各零部件的精度，在机床的几何误差研究中广泛使用，而在半导体加工设备研究领域应用较少[8]。

笔者针对微型晶体谐振器激光调频作动平台的加工工艺和结构特点，对初始加工位置时的探针末端定位误差，运用多体系统理论建立探针末端定位误差模型，运用蒙特卡洛法分析各参数的影响，从而为微型晶体谐振器激光调频作动平台的设计和调试提供理论依据。

1 探针末端定位误差模型

1.1 多体拓扑结构的低序体阵列描述

采用低序体阵列描述多体系统拓扑结构，可将复杂的部件简化为典型体[9]，使得多体系统的拓扑结构更简洁，便于建立误差模型，进行仿真计算。微型晶体谐振器激光调频作动平台结构如图1所示，主要由底板、龙门架、探针、X轴导轨、Y轴导轨、Z轴导轨、固定基座和待加工微型晶体谐振器等组成。加工时，每两根探针对应一根起振条，与同一个微型晶体谐振器的电路部分接触形成回路，起振条固定在机箱中；探针固定在龙门架上，控制各关联轴运动使微型晶体谐振器与探针接触。

图1 微型晶体谐振器激光调频作动平台结构示意图

由于闭环多体系统可以转化为带有特定约束的开环多体系统，因此以开环多体系统为研究对象[10]。取处于初始加工位置，探针与待加工微型晶体谐振器于最佳首触点恰好接触时的微型晶体谐振器激光调频作动平台为研究对象，对探针末端定位误差建模。将微型晶体谐振器激光调频作动平台抽象成多体系统拓扑结构，设底板为惯性体B0，选典型体1为B1体，然后沿远离B1的方向，按自然增长数列，依次为典型体编号，如图2所示。

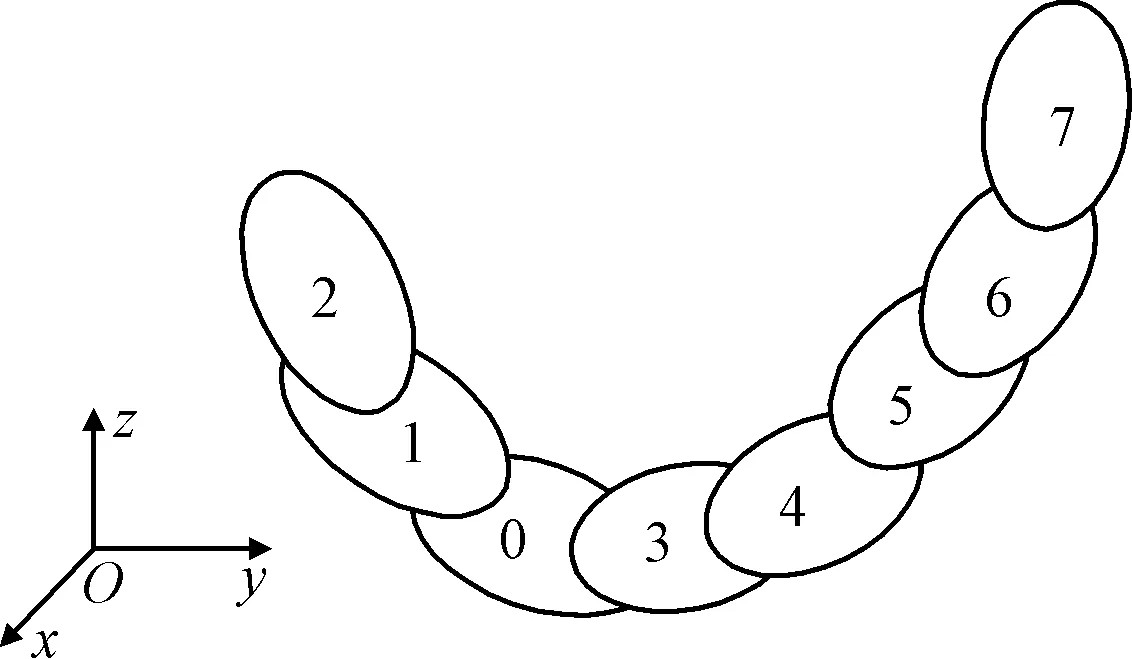
图2 微型晶体谐振器激光调频作动平台的拓扑结构

任选Bj为系统中任意典型体，典型体Bj的n阶低序体的序号定义为：

Ln(j)=i

(1)

式中:L为低序体算子；i和j为典型体的代号，并称体Bj为Bi的n阶高序体，它满足：

Ln(j)=L(Ln-1(j))

(2)

L0(j)=j

(3)

Ln(0)=0

(4)

当体Bi为体Bj的相邻低序体时，有：

L(j)=i

(5)

依此可以得到图2中的多体系统各阶低序体阵列序号，以及整个多体系统拓扑结构的低序体阵列，如表1所示。

表1 微型晶体谐振器激光调频作动平台的低序体阵列

1.2 探针末端定位误差建模

在惯性体B0和典型体Bj、惯性体Bi上分别建立与体固联的静坐标系O0-x0y0z0和动坐标系Oj-xjyjzj、Oi-xiyizi，则点Oj相对点Oi的位置及其变化表征了典型体Bj相对于典型体Bi的平移运动情况，右旋正交基矢量组xjyjzj相对右旋正交基矢量组xiyizi的姿态及其变化表征了典型体Bj相对于典型体Bi的旋转运动状况。典型体Bj相对于其相邻低序体Bi的位置和姿态等价于坐标系Oj-xjyjzj和Oi-xiyizi的相对位置和姿态，进而将多体系统中各体的研究转为对各体坐标系的研究[8]。

对于坐标系Oj-xjyjzj和Oi-xiyizi,用矩阵Tijp和矩阵Tijs来分别描述理想状态下空间点在各坐标系中静止位置坐标变换和运动位置坐标变换，用矩阵ΔTijp和矩阵ΔTijs来分别描述实际状态下空间点在各坐标系中静止位置坐标变换和运动位置坐标变换，位置坐标变换矩阵均采用4×4阶矩阵，参数为欧拉角。将用于描述理想静止和运动的齐次矩阵称之为理想特征矩阵，把用以描述实际静止和运动误差的齐次变换矩阵称为误差特征矩阵。有沿轴平动和绕轴转动两种运动均会产生与其运动量相关的6项误差Δαij、Δβij、Δγij、Δxij、Δyij、Δzij，以沿X轴平动为例，其几何意义如图3所示。

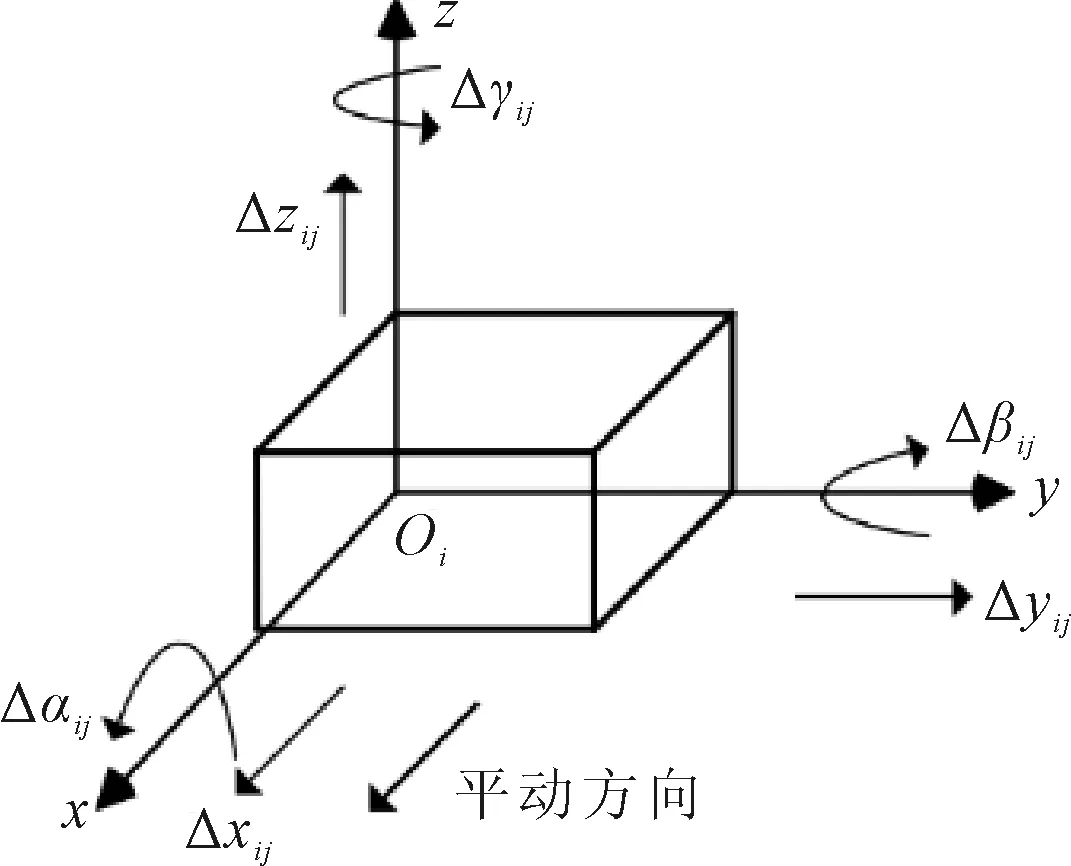
图3 沿X轴平动的6项运动误差的几何意义

在微型晶体谐振器激光调频作动平台的加工过程中，激光与被加工件之间是非接触加工，且加工位置为微型晶体谐振器的音叉部分，探针接触位置为电路部分，因此热效应对探针末端影响极小；探针接触微型晶体谐振器接触面积极小，且接触后相对静止，弹性变形误差影响小，因此所研究探针末端定位误差主要考虑系统的原始误差。根据多体系统理论，微型晶体谐振器激光调频作动平台的体间固定位置误差特征矩阵Tij为：

(6)

由表1中微型晶体谐振器激光调频作动平台的低序体阵建立相邻体间的理想误差矩阵Tij及实际误差特征矩阵ΔTij，为表达更加清晰，矩阵中的下标p、s分别表示静止和运动误差，其中变换矩阵为I4×4时，是指6项运动误差相对很小或者没有。

(1)龙门架固定在底板上，典型体1与典型体0的理想静止误差T01p、理想运动误差T01s、实际静止误差ΔT01p和实际运动误差ΔT01s均相对很小，记作I4×4。

(2)探针固定在龙门架上，典型体2与典型体1的理想静止误差T12p和实际静止误差ΔT12p相对很小，记作I4×4；其理想运动和实际运动的齐次变换矩阵分别为：

(7)

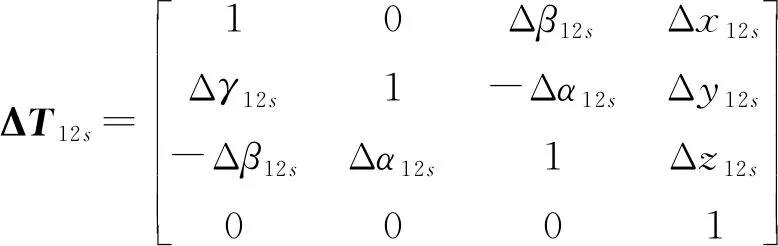
(8)

(3)X轴导轨固定在底板上，典型体3与典型体0的理想静止误差T03p和实际静止误差ΔT03p相对很小，记作I4×4；其理想运动和实际运动的齐次变换矩阵分别为：

(9)

(10)

(4)Y轴导轨安装在X轴导轨上，典型体4与典型体3的理想静止误差T34p相对很小，记作I4×4；其理想运动和实际静止、运动的齐次变换矩阵分别为：

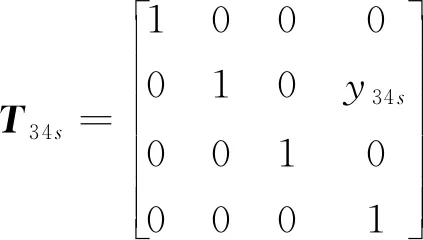
(11)

(5)Z轴导轨安装在Y轴导轨上，典型体5与典型体4的理想静止误差T45p相对很小，记作I4×4；其理想运动和实际静止、运动的齐次变换矩阵分别为：

(14)

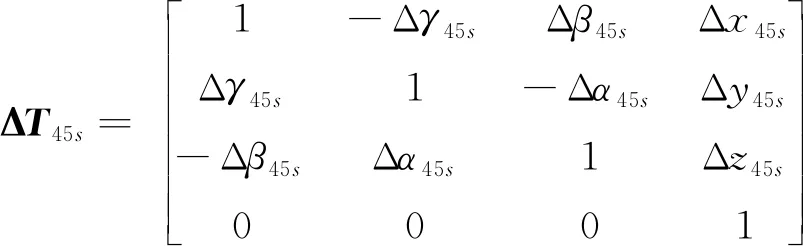
(16)

(6)固定基座安装在Z轴导轨上，典型体6与典型体5的理想静止误差T56p、理想运动误差T56s和实际运动误差ΔT56s相对很小，记作I4×4；其实际静止误差的齐次变换矩阵分别为：

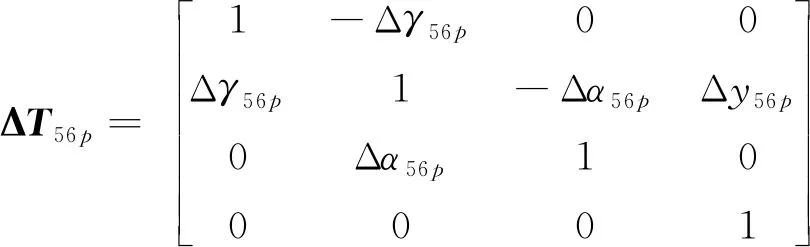
(17)

(7)待加工微型晶体谐振器通过真空负压装载在固定基座上，典型体7与典型体6的理想静止误差T67p、理想运动误差T67s和实际运动误差ΔT67s相对很小，记作I4×4；其实际静止误差的齐次变换矩阵为：

(18)

在多体系统中，惯性体B0和各典型体Bj上均建立起与其固定联接的右手直角笛卡尔三维坐标系，为了简化模型，将在平动、转动过程中产生的误差，通过不同位置矢量的同一实际首触点转化到惯性体坐标系中，从而推导出微型晶体谐振器激光调频作动平台的探针末端定位误差模型。

在理想状态下的初始加工位置，成排探针的第三根探针末端与首排首列微型晶体谐振器的电路部分最佳加工位恰好接触，该点为该探针末端与首排首列微型晶体谐振器的最佳首触点；将探针坐标系中的最佳首触点位置矢量表示为Pt(xt,yt,zt,1),待加工微型晶体谐振器坐标系中的最佳首触点的位置矢量表示为Pw(xw,yw,zw,1)。最佳首触点对于每个微型晶体谐振器均为定点，理想状态下，在广义坐标系O0-x0y0z0中各微型晶体谐振器上的最佳首触点与其对应的探针末端最佳首触点重合；但因各误差因素影响，在广义坐标系中的各微型晶体谐振器上的实际最佳首触点Pw0(xw0,yw0,zw0,1)与对应探针的最佳首触点Pt0(xt0,yt0,zt0,1)难以重合。

结合表1中微型晶体谐振器激光调频作动平台的低序体阵列，待加工微型晶体谐振器上实际最佳首触点在广义坐标系O0-x0y0z0中的齐次坐标变换矩阵[9]为：

Pw0=T07Pw

(19)

T07=T03T34T45T56T67

(20)

其对应探针末端实际最佳首触点位置矢量在广义坐标系O0-x0y0z0中的齐次坐标变换矩阵为：

Pt0=T02Pt

(21)

T02=T01T12

(22)

设E为探针末端定位误差模型，则：

E=Pt0-Pw0

(23)

Ex=xt0-xw0

(24)

Ey=yt0-yw0

(25)

Ez=zt0-zw0

(26)

根据多体系统理论，各典型体固联坐标系间的变化用参数为欧拉角的4×4阶齐次矩阵表示，其表达式为：

Tij=TijpΔTijpTijsΔTijs

(27)

最终得到微型晶体谐振器激光调频作动平台的探针末端定位误差模型为：

E=T02Pt-T07Pw

(28)

2 基于蒙特卡洛法的探针末端定位误差分析

2.1 基于Matlab的探针末端定位误差仿真

根据某型号的微型晶体谐振器尺寸及加工需求，激光调频作动平台的探针末端x、y、z方向的定位精度分别为300 μm、100 μm、100 μm。实际运动误差难以测出，且相对较小，因此通过实验估测加工该型号微型晶体谐振器所用的激光调频作动平台的实际静止的误差取值范围，各误差分量在一定范围内波动，可以利用蒙特卡洛模拟法产生随机数以仿真实际中的误差变化。基于微型晶体谐振器激光调频作动平台的探针末端定位误差模型，使用Matlab软件对微型晶体谐振器激光调频作动平台的静止误差进行编程，仿真进行了250 000次，得到探针末端实际首触点的模拟结果如图4所示，误差的平均值和标准差如表2所示,负号表示该点的误差方向与广义坐标系相反。

表2 探针末端首触点的误差平均值和标准差

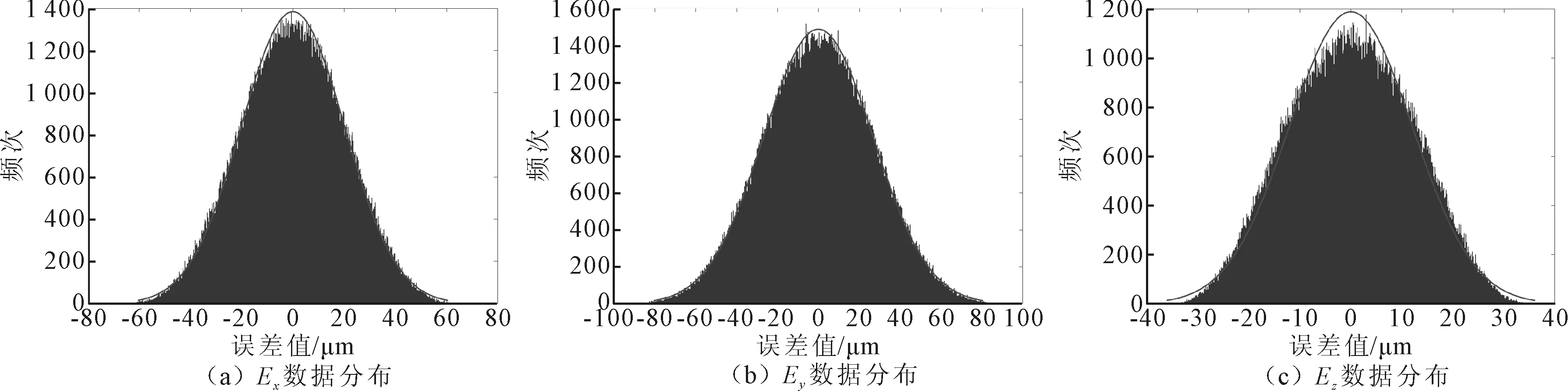
图4 探针末端实际首触点的Ex、Ey和Ez误差分布

2.2 探针末端定位误差仿真分析

由图4可知，探针末端定位误差的x、y、z方向误差均基本符合正态分布特征，各误差数据大部分被正态分布曲线所覆盖，且轮廓与正态分布曲线贴合，因此利用误差数据的正态分布特征来分析误差特征及其应用是合理的。同时，x和y方向的正态分布曲线覆盖率和轮廓贴合均优于z方向。从表2可知，Ex的平均误差值最大，Ey的标准差最大，Ez的平均误差和标准差均最小。加工该型号微型晶体谐振器的激光调频作动平台的定位精度和重复定位精度如表3所示。

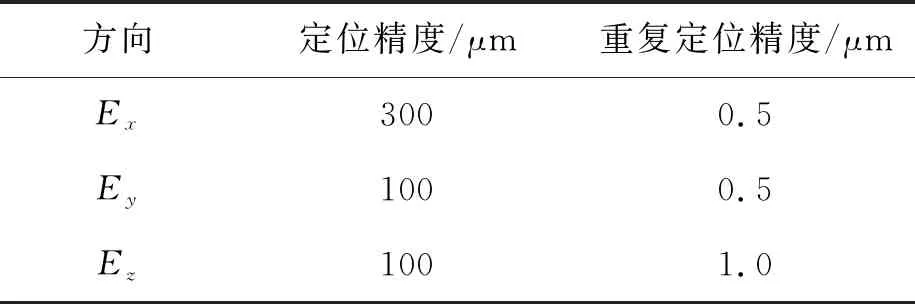
表3 调频作动平台定位精度和重复定位精度

由表3和仿真结果分析可知，调试时以各探针末端共成平面为基准，y方向和z方向为主要调试对象，x方向和y方向均校正完毕后再修正z方向，在初始加工位置主动折弯探针30 μm可提高加工效率并减少损耗。

3 结论

笔者根据微型晶体谐振器激光调频作动平台的加工工艺和结构特点，针对微型晶体谐振器激光调频作动平台的探针末端定位问题，从探针末端与微型晶体谐振器的理论最佳首触点出发，运用多体系统理论得到相邻典型体间的理想静止、运动和实际静止、运动的齐次变换矩阵，建立了探针末端定位误差模型。对于平台误差难以精确测量的问题，利用Matlab软件编程，运用蒙特卡洛模拟法对平台静止误差取值范围进行分析，得到探针末端实际首触点的x、y、z方向的仿真结果，分析仿真结果并结合实际，为设备调试提供指导，并为提高平台的精度和品控提供理论依据。