深部富水岩石拱形隧道地震响应解析解

禹海涛，陈功

(1.同济大学土木工程防灾国家重点实验室，上海，200092；2.同济大学岩土及地下工程教育部重点实验室，上海，200092；3.同济大学地下建筑与工程系，上海，200092)

随着我国西部交通基础设施建设的不断推进，地下工程发展迅速，目前已建设大量山岭隧道，这些隧道具有埋深大、地层条件复杂等特点。近年来地震频发，如日本阪神地震[1]、中国台湾地震[2]、中国汶川地震等[3]均对山岭隧道造成了不同程度损坏，引起了研究者和工程设计人员的广泛关注。在实际工程中，岩石隧道往往采用拱形断面形式，其地震响应特征与圆形隧道相比较复杂。而对于穿越富水地层的隧道，地下水的存在往往会使其地震响应更加复杂，因此，研究深部富水岩石拱形隧道的地震响应具有实际意义。目前，针对隧道结构的抗震研究以数值模拟或模型试验为主。如AMOROSI 等[4]采用有限元方法研究了黏性地层中圆形隧道的横向地震响应；PARK 等[5]通过在隧道地震响应分析中引入拟静力假定，提出了一种简化的三维有限元分析方法；YU等[6−8]采用多尺度方法分析了长隧道在一致和非一致地震作用下的动力响应规律；袁勇等[9−12]基于多台面振动台模型试验，研究了长大隧道在非一致激励下的地震响应机制；对于拱形隧道，信春雷等[13]通过振动台模型试验研究了跨断层拱形隧道的减隔震方法，施有志等[14]建立三维有限元模型研究了大断面拱形双隧道的地震响应特征。采用数值方法进行隧道地震响应分析耗时较长，同时计算结果易受地层的本构参数、地层−结构相互作用方式、人工边界等多因素影响，而模型试验方法成本较高且费时费力，故这2种方法均不便于直接应用于实际工程设计。目前工程设计通常采用拟静力法如自由场变形法、地层−结构相互作用法进行隧道地震响应分析。自由场变形法将地震动的自由场变形直接施加在衬砌上，然后计算结构的内力。基于此方法，KUESEL等[15]为旧金山的明挖与暗挖矩形隧道提出了一个通用的设计标准。但隧道会改变地层的地震动特性，使得自由场变形法计算得到的结果往往误差较大，因而，工程设计一般采用精度更高的地层−结构相互作用法。目前，许多研究者基于该方法提出了计算地震响应的解析方法。BOBET 等[16−18]考虑了隧道深埋与浅埋以及地层排水与不排水等条件，推导了圆形隧道的地震响应解析解。针对矩形隧道，HUO等[19−20]对深埋条件下矩形隧道进行了解答。此类解析方法具有使用方便、计算效率高、参数易选取等优点，在实际工程中备受设计人员青睐，但目前研究仅限于圆形或矩形等简单截面形状。本文基于地层−结构相互作用的拟静力方法，综合考虑地层不排水(undrained)与全排水(drained)这2 种典型工况以及地层−结构交界面上不滑移(no-slip)和全滑移(fullslip)这2种接触条件，使用保角映射方法，推导深部富水岩石拱形隧道地震响应解析解。通过与有限元模拟结果对比分析，验证本文解析解的有效性。在此基础上，应用该解析解对地层−结构相对刚度比、地层−结构接触条件、地层排水条件、衬砌厚度等因素对深埋拱形隧道地震响应的影响规律进行分析。

1 模型假定与控制方程

本文针对地震剪切波作用下的深部富水岩石拱形隧道结构进行研究。隧道−地层相互作用体系和坐标系如图1所示，其中，Eg和El分别为地层和衬砌的弹性模量，vg和vl分别为地层和衬砌的泊松比，τ为地震荷载拟静力等价的远场剪应力，φ为衬砌任一位置点关于x轴的夹角，δ为衬砌厚度。

图1 远场剪应力作用下的深部富水岩石拱形隧道Fig.1 Deep arch tunnel subjected to far-field shear loading

1.1 基本假定

在推导计算中进行如下假定：

1)地层与衬砌沿纵向的应变均为0，计算模型满足平面应变假设。

2)采用多孔介质模型计算地层，地层为饱和各向同性线弹性体，衬砌为各向同性线弹性体。

3)鉴于隧道埋深较大，在地震响应分析的拟静力方法中，可将地震荷载简化为远场剪应力。

4)衬砌厚度相比隧道高度可以忽略，采用壳体模型计算衬砌受力。

衬砌的控制方程可以由弹性力学中壳体的一般理论得到[23−24]。

1.2 控制方程

1.2.1 地层

根据多孔介质理论[21]，平面应变条件下地层的应力可以通过Airy应力势函数φ表示。在图1所示的xOy坐标系下有

式中：σgx，σgy和τgxy为地层中任一点的应力分量，σgx′和σgx′为地层中任一点的有效应力分量，以受拉为正；u为地层中任一点的孔隙水压力。在平面应变条件下φ和u满足如下关系

式中：K为地层的渗透系数；γw为水的重度；ζ为地层中任一点体积含水率的变化量；t为时间；∇2为Laplace算子。

对饱和地层的地震响应进行分析时，通常假设地层不排水和全排水这2个极端工况，以简化分析过程[16−17,22]。对于不排水工况，即在地震作用的瞬间，地层中的超孔压没有来得及消散，此时地层中流体的体积变化为0(ζ=0)。则土骨架的体积应变为0，有

将式(3)代入式(1)，有

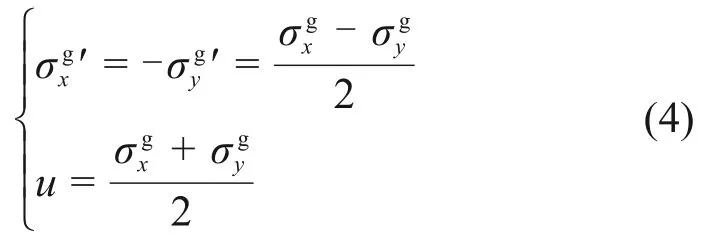
对于全排水工况即地震引起的超孔压完全消散，u为0，计算模型等价于地层无水条件，式(2)均退化为∇2(∇2φ)=0。

采用复应力势函数φ(z)和ψ(z)表示Airy应力势函数，则在不排水与全排水条件下，饱和地层的应力与位移可以表示为[22]

式中：z=x+iy，i为虚数单位；Gg为地层的剪切模量。对于不排水条件，κ=1，对于全排水条件，κ=3-4vg；vg为地层的泊松比。

1.2.2 衬砌

衬砌的控制方程可以由弹性力学中壳体的一般理论得到[23]。

式中：T与M分别为衬砌单位纵截面上的轴力与弯矩；s为衬砌的弧长；δ为衬砌的厚度；El与vl分别为衬砌的弹性模量与泊松比。衬砌的平衡方程为

将式(6)代入式(7)，可以得到衬砌受力与位移之间的关系：

式中：σlρ和σlθ为衬砌与地层的法向和切向接触应力；ulρ和ulθ分别为衬砌的法向和切向位移；K为衬砌上任一点的曲率；K′=dK/ds。衬砌受力与位移如图2所示。

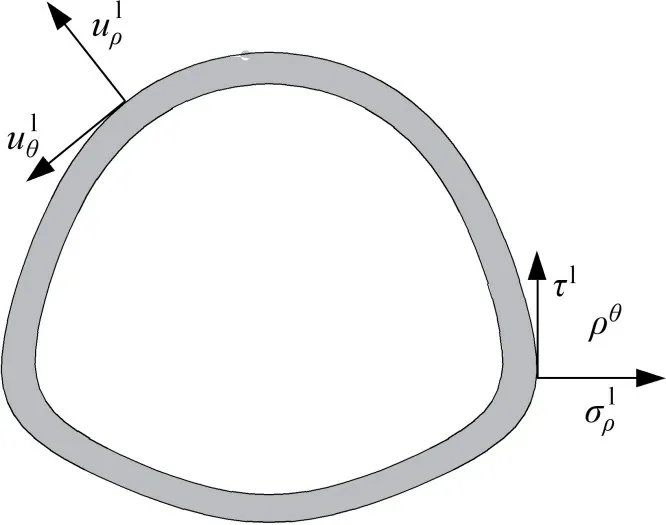
图2 衬砌受力与位移Fig.2 Stresses and displacements of liner

1.2.3 边界条件

对于远场边界条件，根据拟静力假定，地震剪切波可以简化为远场剪应力，剪应力为[17−19]

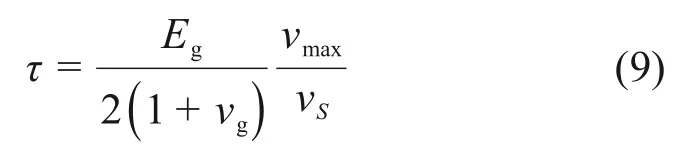
式中：vmax为地震动的峰值速度；vS为场地剪切波速。地层与衬砌不滑移时，即地层与衬砌的应力与位移在接触面上连续，有

地层−结构完全滑移即地层与衬砌的法向应力与法向位移在接触面上连续，且切向应力为0时，有

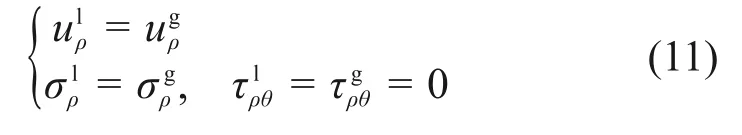
2 解析解

2.1 保角变换

使用保角变换方法，将z平面上的拱形隧道映射成ζ平面上的单位圆Θ=eiθ，建立地层的应力与位移的解析表达式。保角映射的一般表达式为[25]

式中：R和Ck为实常数。将ζ平面上的极坐标ζ=ρeiθ代入式(12)，可以得到z平面上一个正交坐标系{ρ,θ}，如图3所示。

图3 {ρ,θ}坐标线Fig.3 Coordinate lines of{ρ,θ}

地层受远场剪应力τ作用，地层的复势函数可以表达成如下形式[25]：

式中：ak和bk为实数；i 为虚数单位。为了简化分析，在计算中只考虑级数中的前N项，本文取N=100，并记

根据弹性力学中的转轴公式，{x,y}坐标系与{ρ,θ}坐标系下的应力与位移有如下关系：

将式(12)与式(16)代入式(7)，可以求解出{ρ,θ}坐标系中地层−结构交界面上的应力与位移分量：

式(17)中应力位移均为φ1(Θ)，ψ1(Θ)及其导数与共轭函数的线性组合。因此，和ugθ关于Θ的Laurent 级数展开式的各阶系数可以表示为Xk的线性组合：

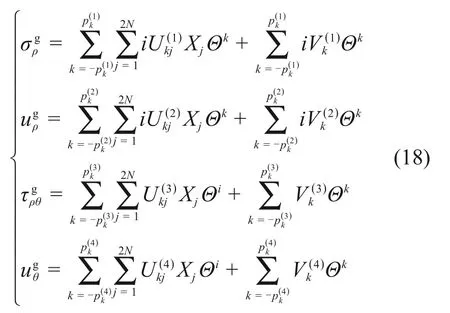
式中：为k阶Laurent 系数中Xj的系数；为常数项。

式(18)给出了{ρ,θ}坐标系下地层−结构接触面上地层的应力与位移，可结合衬砌的控制方程与边界条件建立σρg，，ugρ和ugθ之间的关系式。为此，将式(8)改写成{ρ,θ}坐标系下的微分方程，有

式中：A*k和Kk分别为1/|ω′(Θ)|和K的各阶傅里叶系数；i 为虚数单位；1/|ω′(Θ)|和K可以由式(13)计算。

2.2 求解待定系数

2.2.1 地层−结构不滑移条件

当地层−结构不滑移时，将式(10)，(18)和(19)代入式(8)。因为式(8)是关于σρl，，ulρ和ulθ的线性微分方程，故该方程左侧同样可以展开为关于Θ的Laurent级数，其各阶系数为Xk的线性组合，有

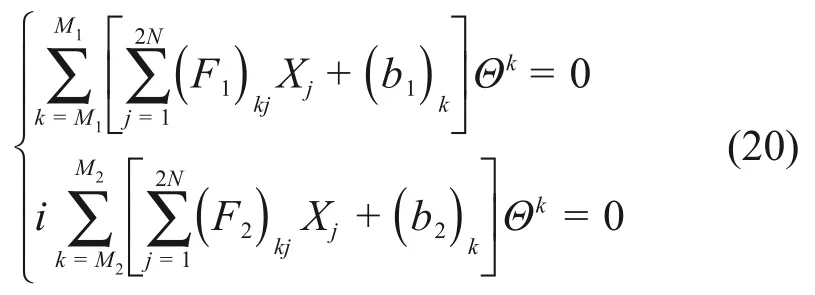
对于任意取值的Θ，式(20)均成立，故其中各阶Laurent系数均为0，有

则待定系数Xk可由式(21)解出。

2.2.2 地层−结构全滑移条件

当地层−结构全滑移时，将衬砌的切向位移ulθ进行傅里叶展开，有

记X2N+1+k=dk，其中，k=0,1,…,N。将式(11)，(18)，(19)和(22)代入式(8)，有

将地层−结构接触面切向应力=0 代入式(18)，有

联立式(23)和(24)，可求解出待定系数Xk。

2.3 衬砌与地层的地震响应

将式(12)代入式(5)，有

将所求Xk代入式(12)，可以计算地层任意一点上的φ1(ζ)和ψ1(ζ)。则地层中各点的应力与位移分量可由式(23)求得。

当地层−结构不滑移时，将所求Xk代入式(15)可求出衬砌的法向与切向位移ulρ和ulθ。当地层−结构全滑移时，将Xk分别代入式(15)和(20)可求出ulρ和ulθ，则衬砌的轴力T与弯矩M可以由式(6)计算[20]。

3 数值验证

建立基于ABAQUS 有限元软件的基准模型，以验证本文解析解的正确性。假设某拱形隧道高为6.45 m，宽为7.3 m，衬砌厚度δ为0.5 m，弹性模量El为30 GPa，泊松比vl为0.2。围岩弹性模量Eg为10 GPa和5 GPa，泊松比vg为0.25。隧道映射函 数ω(ζ)的各项系数为[26]：R=3.409，C0=-0.067 3，C1=-0.059 3，C2=0.067 2，C3=-0.002 8，C4=-0.0211，C5=0.007 4。

隧道衬砌用梁单元模拟，富水地层用四结点平面应变孔压单元模拟，远场剪应力取为τ=1 MPa。对于不排水条件，采用soil 分析步计算地震荷载施加的瞬态响应；对于不滑移条件，地层−结构接触面使用绑定约束；对于全滑移条件，地层−结构间法向为硬接触，切向为无摩擦接触面。衬砌内边界的切向正应力为σθ=T/δ+Mδ/(2I)(式中，I为衬砌单位纵截面的转动惯量，I=δ3/12)。

图4所示为不排水不滑移、不排水全滑移、全排水不滑移、全排水全滑移条件下有限元数值方法与本解析方法的结果对比。从图4可以看出本文解析解与数值解基本一致，从而验证了本文解析解的正确性。

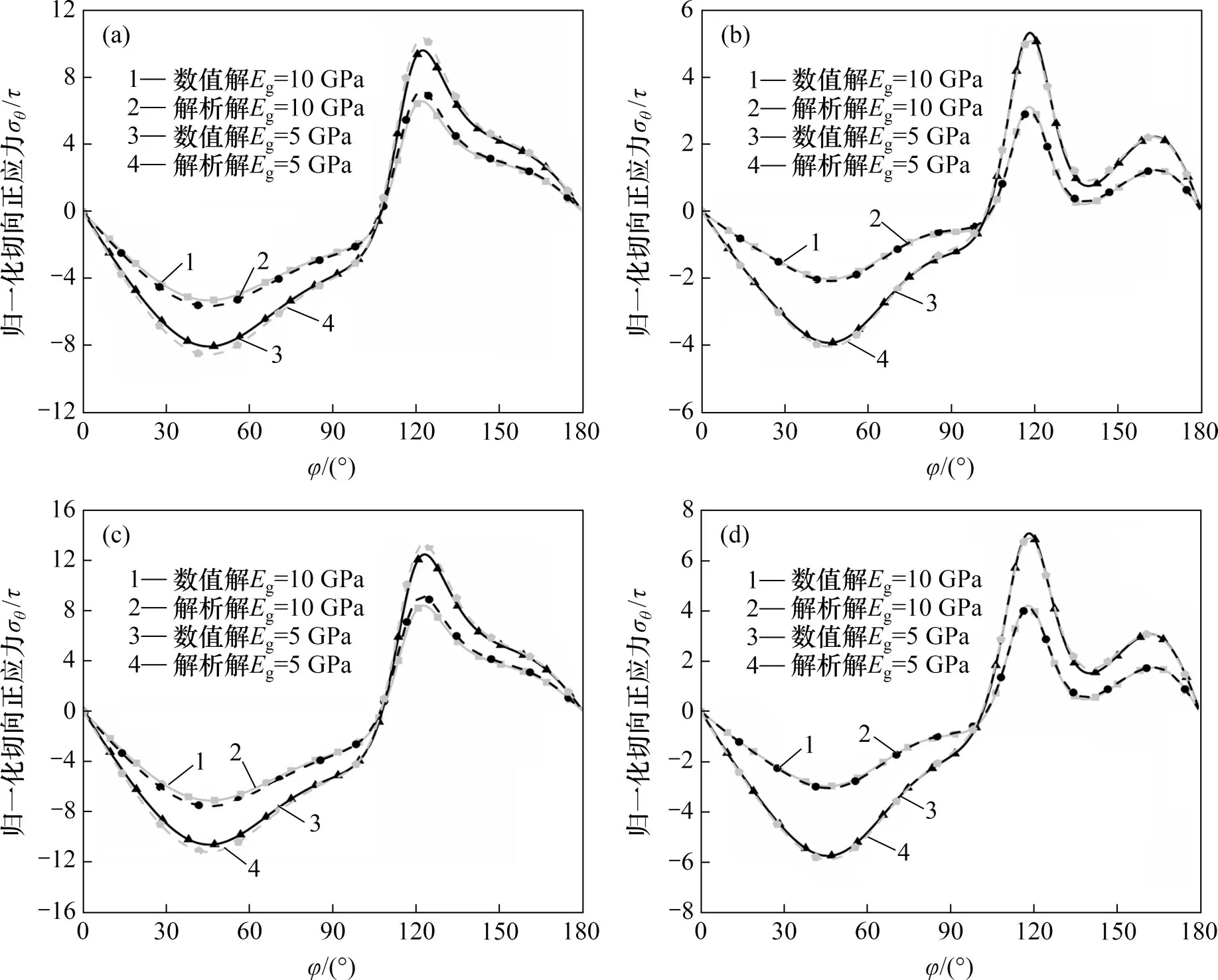
图4 拱形隧道地震响应对比验证Fig.4 Comparisons of seismic responses of arch tunnels between FEM model and analytical solutions

4 参数化分析

应用本文解析解可以方便地分析各关键参数对隧道内力响应的影响，本节选取地层−结构相对刚度比、衬砌厚度等关键参数进行敏感性分析，并比较地层不同排水条件、地层−结构不同接触条件下隧道的地震响应特性。

4.1 地层−结构相对刚度比的影响

通常隧道的地震响应主要受控于结构−地层相对刚度比。地层−结构相对刚度一般由柔度比(flexibility ratio)或刚度比(stiffness ratio)描述，两者互为倒数。参考圆形隧道柔度比的定义[16]，定义拱形隧道的柔度比F为

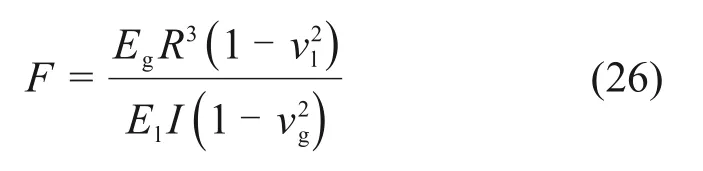
通过改变地层的弹性模量，分析柔度比对隧道地震响应的影响，地层弹性模量取0～7.703 GPa。图5所示为柔度比对衬砌内边界上归一化切向正应力σθ/τ最大值的影响规律。从图5可见：随着柔度比增大，隧道的最大内力响应逐渐减小，且最大内力响应在柔度比较小时速率降低较快，而随着柔度比增大趋于平缓；当柔度比F较大时，隧道的最大内力响应对柔度不太敏感；在地层−结构不滑移条件下，当柔度比较小时，隧道的最大内力响应受地层排水条件影响较小，而当柔度比较大时，隧道的最大内力响应在全排水条件下较大；在地层−结构全滑移时，全排水条件时的响应均略大于不排水条件时的响应；在相同的地层排水条件下，地层−结构不滑移时的响应大于全滑移时的响应。

图5 柔度比对拱形隧道最大内力响应的影响Fig.5 Effects of flexibility ratio on the maximum stress responses of arch tunnels

图6所示为柔度比对隧道归一化法向位移2Gulρ/(τR)最大值的影响规律。从图6可见：与隧道的内力响应不同，隧道的最大位移响应随着柔度比增大而增大；当柔度比F较大时，隧道的最大位移响应受地层排水条件影响较大，全排水条件下隧道的位移响应显著大于不排水条件的响应；当地层不排水时，不滑移与全滑移接触条件下隧道的最大位移响应差别很小。

图6 柔度比对隧道最大法向位移响应的影响Fig.6 Effects of flexibility ratio on the maximum displacement responses of arch tunnels

4.2 衬砌厚度的影响

图7所示为不排水不滑移条件下，不同厚度隧道的弯矩、轴力、衬砌内边界切向应力的分布关系。由图7可见：随着衬砌厚度增大，隧道的弯矩响应显著增大，不同厚度下隧道的弯矩响应相差较大；对于轴力响应，衬砌厚度增大会导致轴力逐步增大，但增大速率较小；而对于衬砌内边界切向应力与衬砌的法向位移，增大衬砌的厚度并不会使其出现较大变化。因此，在岩石地层隧道结构抗震设计中，应综合考虑结构内力、应力与位移响应选择合适的衬砌厚度。

图7 不排水条件下衬砌厚度对拱形隧道内力响应的影响Fig.7 Effects of thickness of liner on stress responses of arch tunnels with undrained condition

5 结论

1)基于保角映射与复变函数方法推导出深部富水岩石拱形隧道地震响应解析解，并综合考虑了地层不排水与全排水以及地层−隧道接触面上不滑移与全滑移等条件。通过与有限元数值结果对比分析，验证了本解析方法的正确性，表明本解析解可以精确描述拱形隧道的地震响应，从而为深部富水岩石拱形隧道地震响应分析和抗震设计提供了新的快速计算方法。

2)随着地层−结构柔度比增大，隧道的最大内力响应减小，而最大位移响应增大。相比地层不排水条件，全排水条件下隧道地震响应均较小，因此，富水岩石地层隧道结构抗震设计应重视排水条件的影响。

3)地层−结构不滑移条件的隧道内力响应大于全滑移条件的响应。在地层全排水时，不滑移条件的隧道位移响应小于全滑移时的位移响应，而在地层不排水时，不滑移与全滑移接触条件下隧道的位移响应基本接近。因此，实际隧道抗震设计应综合考虑地层−结构之间的全滑移和不滑移这2种极端接触状态。

4)衬砌厚度对衬砌的内力与弯矩响应均有显著影响，但对衬砌的最大法向位移和内边界切向应力影响可以忽略不计。因此，在结构设计中应该合理选取衬砌厚度，避免通过盲目提高衬砌厚度来提高结构的抗震性能。