空间面板数据模型在地面气温观测资料质量控制中的应用

熊雄 姚薇 张颖超

(1 南京信息工程大学 江苏省大气环境与装备技术协同创新中心，南京 210044；2 江苏省突发事件预警信息发布中心，南京 210019；3 南京信息工程大学 气象灾害预报预警与评估协同创新中心，南京 210044)

引 言

大量观测实验和数值计算模拟表明，数值天气预报已成为开展现代气象业务的主要手段之一，而资料同化技术是保障数值天气预报准确性的前提[1]，地面气温资料进行质量控制将有助于资料同化及数值天气预报水平的提高[2-5]。

对地面气温观测资料质量控制算法的研究遵循从单站到多站联网研究的技术路线，逐步由气象要素物理约束向气象要素时空关联性拓展，从一维空间向多维空间延伸。一般而言，地面气温观测资料的质量控制算法可以分为两类[6-7]：一类是利用邻近站信息对目标站进行多站联网质量控制；另一类则是从时序相关性、观测要素自约束性等角度对目标站地面气温观测资料进行单站质量控制。大量研究表明，在邻近站观测信息满足参考条件情况下，多站联网质量控制要比单一观测站质量控制的效果好[8]。随着国家气象局在全国范围内的“三站四网”大气监测工程的建设，地面气温观测资料进行多站联网质量控制成为一个发展趋势[9]。根据实际情况的不同，国内外气象学者们对地面气温观测资料质量控制算法开展了不同的研究。维也纳大学的学者们提出变分质量控制法[10]，该算法的基础是计算一个观测场与背景场的代价函数及其误差协方差的最小值，本质上是一个最优控制问题。我国学者在地面气温观测资料的研究中也有不少创新尝试，ZOU，et al[11]从服务资料同化的角度出发，通过对比观测场和背景场观测差异，提出了基于高斯分布和经验正交函数分解等地面观测资料质量控制方法；YE, et al[12]提出基于智能方程拟合的方法从时空回归角度来构建质量控制方程实现对地面气温数据进行质量控制，拓展了学者们研究气象数据质量控制问题的领域。XU, et al[13]在业务层面上，对地面资料质量控制方案提出了不同的修订方案。从现有的研究来看，地面气温观测资料质量控制算法均是从单一的维度去构建质量控制方程，势必造成质量控制方程的不稳定性。

因此，本文提出了一种基于改进空间面板数据模型的地面气温观测资料的多站质量控制算法(ST-RH算法)。利用一定区域范围内地面气温时空相关性信息构造空间面板数据模型，并将相对湿度作为解释变量融入算法，实现对目标站地面气温观测资料质量控制。该算法的出发点是设定地面气象观测资料的时空分布具有空间面板数据的结构特征，即地面气象观测资料的排放是先将某个时间节点区域范围内观测站资料堆放在一个横截面上，再将不同时间节点的横截面数据按时间顺序堆放在一起。为了检测ST-RH算法的有效性和普适性，利用国家气象信息中心提供的国家级地面站观测资料，通过多组独立试验对ST-RH算法进行检测，并结合多个质量控制算法评价指标与IDW算法和SRT算法进行对比分析。

1 资料和方法

1.1 资料

本文所涉及地面气温、相对湿度观测资料均经过了严格的“台站—省级—国家级”三级质量控制，剔除了明显的粗大误差。文中所涉及国家级地面站(目标站)及其周围90 km范围内邻近站见表1所示。

表1 全国14个典型地面观测站半径90 km范围内邻近站数目Table 1 Numbers of neighboring stations within 90 km radius of14 surface observation stations

选取的14个目标观测站分布在我国不同的地区，所属的气候、地形和地貌等环境各异，便于检测ST-RH算法的普适性和稳定性：改则站位于青藏高原，属高原山地气候，地形地貌简单，但邻近观测站站分布稀少；天池站、酒泉站位于西北地区，靠近亚洲高原源地，大陆性结构特征强；包头站、伊春站位于高纬度的黑龙江和内蒙古的北部地区；四平站、怀柔站和忻州站位于华北和东北地区及黄土高原地区，地形地貌多样，特别忻州站处于山地区域，小气候环境复杂；绵阳站、浏阳站、南京站和赣州站均位于水系、山地复杂区域，气候环境多变；东莞站、三亚站位于南部沿海地区。

为了检测算法的质量控制效果，本文在目标站地面气温观测资料中随机选取占总样本3%作为人为植入误差[14]，大小如式(1)所示：

Ex=sx·qx,

(1)

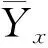
(2)

1.2 常规空间面板数据模型

常规空间面板数据模型分为空间滞后模型(SLM)和空间误差模型(SEM)两类，其数学表达形式分别为：

y=δ(IT⊗W)y+Xβ+(τT⊗IN)μ+ε，

(3)

y=Xβ+(τT⊗IN)μ+u,u=ρ(lT⊗W)u+ε，

(4)

其中：T为时间序列长度；N为空间单元个体数；y为NT×1的因变量；X为NT×K的解释变量；K为解释变量个数；δ和ρ是空间自回归系数；β是K×1解释变量系数列向量；IT和IN分别是T×T和N×N的单位矩阵；τT是T维元素全为1的列向量；⊗表示克罗内克(Kronecker)积；μ代表个体效应；u和ε分别都为独立分布的随机误差项，均服从均值为0；方差为σ2的正态分布；W是行标准化了的N阶方阵。W用来反映数据空间相关性，一般情况下，空间权重矩阵的设定为：若个体i与个体j相邻，则Wij=1，否则Wij=0，Wij为W中的元素。

空间滞后模型和空间误差模型在处理不同问题时各有优缺点，如何选择合适的空间面板数据模型至关重要。YING,et al[15]在拉格朗日乘数(LM)检验的基础上[15]，分别提出了检验空间误差模型的准则LMERR和检验空间滞后模型的准则LMLAG，数学表达式分别如下：

(5)

(6)

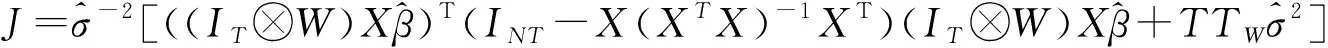
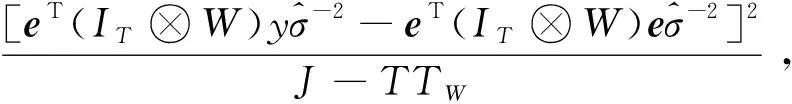
(7)

(8)

运用空间面板数据模型对地面气温观测资料进行质量控制时，SLM对应的原假设为H0：无空间滞后因变量；SEM对应的原假设为H0：无空间误差项。无论是SLM还是SEM，若LM通过5%水平下的显著性检验，则拒绝原假设，说明存在空间效应，适合用空间面板数据模型对数据进行分析，反之接受原假设；在通过显著性的前提下，若robustLMERR>robustLMLAG，则选择空间误差模型，否则选择空间滞后模型。

当空间效应存在时，分别采用普通最小二乘法(OLS)对空间滞后模型和空间误差模型进行参数估计可得出结论：对于SEM模型来说模型的参数估计是无偏的，但不具有效性；对SLM模型来说模型的参数估计则为有偏且不一致。因此，在考虑空间效应存在时，本文拟采用极大似然(ML)法对模型参数进行估计。

1.3 基于改进空间面板数据模型的地面气温观测资料质量控制算法(ST-RH算法)

利用空间面板数据模型对地面气温观测资料进行质量控制本质上是运用空间回归技术结合邻站的观测信息对目标站观测值的回归估计。地面气温在空间的分布连续、平稳，满足空间相关性的条件；同时，由于地形地貌等小气候环境的存在，不同空间观测单元对应的观测资料之间也存在着明显的异质性。从而保证了空间面板数据模型在地面气温观测资料质量控制中运用的理论可行性。

本文选取以南京站为中心及其周围90 km范围内邻站2017年7月逐时气温和相对湿度观测资料为例，对基于空间面板数据模型的地面气温观测资料质量控制算法进行实例阐述。涉及地面气象观测资料时间序列长度。通过计算，南京站2017年7月逐时气温观测资料空间相关性检验如表2所示：

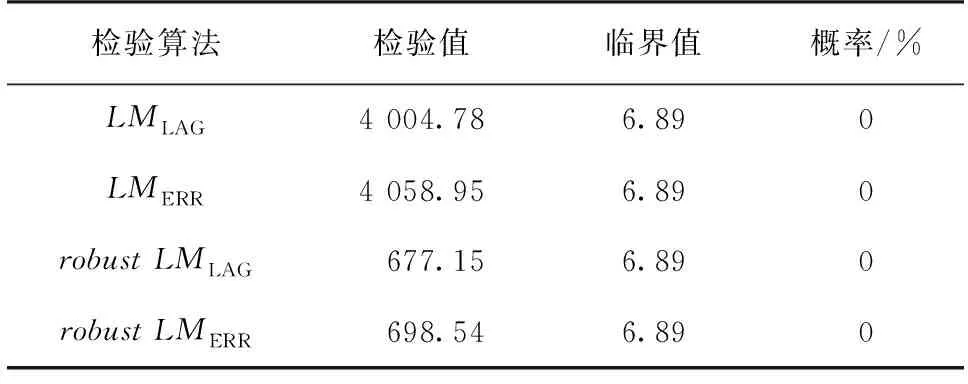
表2 2017年7月南京站逐时地面气温观测资料空间相关性检验 Table 2 Inspection of spatial correlation of hourly surface temperature observations for Nanjing station in July 2017

由表2可以看出无论是经典LM测试还是稳健LM测试，原假设在1%显著条件下都被拒绝，通过显著性检验，表明存在空间相关性。同时检验因子LMERR>LMLAG，robustLMERR>robustLMLAG，分别对本文涉及的其它13个地面观测站进行空间相关性检验均得到相同结果，说明采用空间误差模型更适合地面气温观测资料的质量控制。

地面气温观测资料在空间维度和时间维度上均是连续的，同时文献[17]指出在对流层的底部，气温与相对湿度具有明显的强耦合关系。为了增加质控模型的内部复杂度与稳定性，本文在空间误差模型的基础上加入时间维度气温信息作为协同变量，加入相对湿度信息作为解释变量强化模型的鲁棒性。因此，基于空间面板数据模型的地面气温观测资料质量控制算法(ST-RH算法)可以描述为公式(9)所示：

y=Xβ+ω(IT⊗τN)η+(1-ω)(τT⊗IN)μ+
[INT-ρ(IT⊗W)]-1ε，

(9)

其中：τT是T维元素全为1的列向量；τT是N维元素全为1的列向量；μ和η分别代表个体效应和时间效应；INT为NT×NT的单位矩阵；ω为地面气温观测资料的时间维度和空间维度协调系数，其计算如式(10)所示：

(10)

其中：ρ1为地面气温观测资料空间维度相关联系数；ρ2为地面气温观测资料时间维度相关联系数。为了便于计算，减少异方差，本文中用lny和lnX分别表示取对数后的逐时气温和相对湿度数据，则公式(9)可以改写为：

lny=C+lnXβ+ω(IT⊗τN)η+
(1-ω)(τT⊗IN)μ+[INT-ρ(IT⊗W)]-1ε，

(11)

其中：C为常数项，通过式(11)可以得到南京站2017年7月逐时气温观测资料预测值，记为yest。若预测值与观测值的差值的绝对值满足公式(12)条件，则认为数据可信，否则标记为存疑数据：

|yobs-yest|≤f·δ，

(12)

其中：yobs为目标站的观测值；yest为目标站的预测值；δ为预测值与观测值的标准差；f为质量控制参数。

1.4 模型评估指标

本文通过宏观检错率来考察算法的质量控制效果，宏观检错率是错误检出个数与实际插入的错误个数之比。在地面气象观测资料质量控制研究中通常存在两类统计学错误：第一类错误：“去真”错误，即把真当假，第二类错误：“纳伪”错误，即以假充真。从宏观角度来说，当第一类错误变大时，第二类错误将变小；反之，第一类错误变小时，第二类错误将变大。为了权衡、量化两类统计错误发生的概率，文献[18]提出均方根检错率概念(MSR)作为评价质量控制算法的考核指标，MSR数学表达如下：

(13)

其中：r1为第一类错误出现概率；r2为第二类错误出现概率；α为r1权重。通常情况下，α的设置调和了r1与r2对MSR的影响，综合评估两者在地面气温观测资料质量控制中的重要性。此外，纳什效率系数(NSC)、平均绝对误差(MAE)和均方根误差(RMSE)也常用来作为评价质量控制模型的评价指标：

(14)

(15)

(16)

2 结果与讨论

以南京站为中心及其周围90 km范围内邻站2017年逐时气温观测资料为例，检验ST-RH算法的质量控制效果，并与IDW和SRT两种算法比较，试验结果如图1所示。图1a可以看出ST-RH算法在各月的宏观检错率均高于SRT和IDW的宏观检错率(特别是在1、8、12月)。由于SRT算法是根据均方根误差来分配权重的；IDW算法是根据欧氏距离来分配权重的；而ST-RH算法是在通过地面气温观测资料的时空相关性来进行回归预测的，同时考虑到相对湿度与气温之间的强相关性，将相对湿度作为解释变量融进算法之中，进一步增强了ST-RH算法的内部稳定性。此外，从图1a中也可以看到SRT和IDW两种传统算法的比较：SRT的宏观检错率在1月和3月出现低于IDW的宏观检错率的情况，2月的宏观检错率与IDW算法基本上持平，其他月份的宏观检错率均高于IDW的宏观检错率。因此从图1a中看到春、冬季的宏观检错率相对于夏季而言较高，但是由于受到随机误差概率分布等因素的影响，难免出现IDW宏观检错率高于SRT宏观检错率的情况。图1b中展示的是IDW、SRT和ST-RH 3种算法在不同月份宏观检错率的宏观分布情况。可以看到，ST-RH算法在不同月份的宏观检错率平均值、最高值和最低值均优于其它两种方法；SRT算法要略优于IDW算法。

图1 ST-RH、SRT和IDW3种算法对南京站2017年逐时气温观测资料质量控制对比分析：(a)不同月份宏观检错率对比；(b)全年宏观检错率对比Fig.1 Performance of ST-RH、SRT and IDW methods for the quality control of surface observations for Nanjing station in July 2017: (a) Macro error ratio for different months; (b) Macro error ratio during 2017

ZOU， et al[11]在对地面气温观测资料质量控制研究中指出，质量控制的目的不仅是去除错误的观测数据，而且可使资料能够更好地同化服务。资料同化最重要的一个假设条件是观测场和背景场的误差分布应尽可能地满足高斯分布。鉴于此，本文选取欧洲中期天气预报中心(ECMWF)的ERA-Interim再分析资料作为背景场资料，通过残差分布情况检测地面气温观测资料经ST-RH、SRT和IDW算法控制后的可利用性。分析图2a—c中频数拟合分布可以看到，图2a更加接近于正态分布，图2b、 c中残差的分布不确定性更强一点。图2d—f中的Q-Q图进一步检验残差的分布，图2d呈现一种比较理想的分布状态，而图2e、 f中的散点头部和尾部均与理想状态有一定的差距。图2表明，相比较于SRT方法和IDW方法，经过ST-RH算法质量控制后的地面气温观测资料与背景场资料的残差分布更具正态分布的特征。

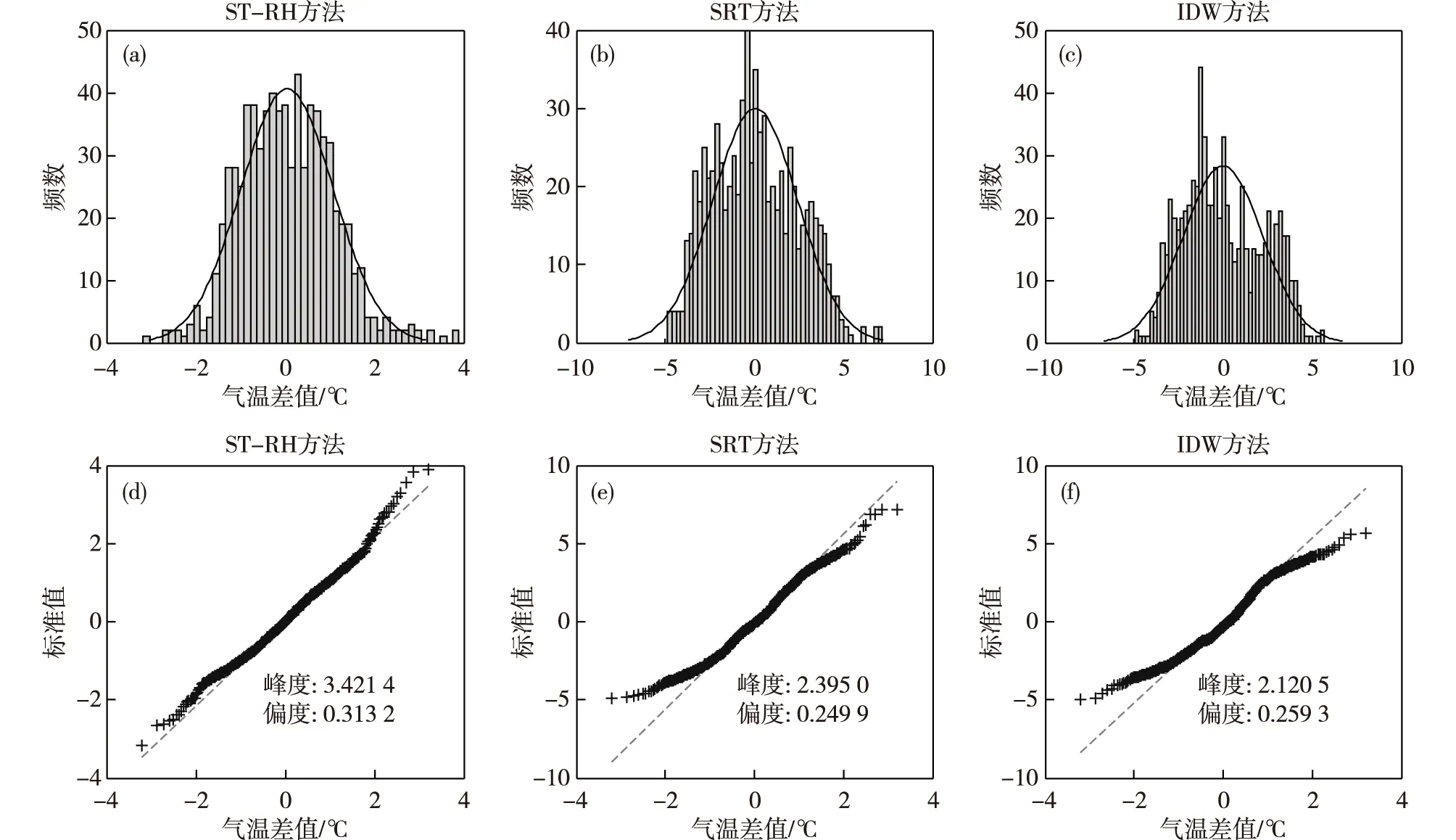
图2 ST-RH、SRT和IDW 3种算法对南京站2017年7月逐时气温观测资料质量控制后与背景场对比残差：(a—c)频数分布；(d—f)残差Q-Q分布Fig.2 Performance of ST-RH、SRT and IDW methods for comparison of residual plots with background field and the observations for Nanjing station after quality control: (a-c) frequency distribution diagram;(d-f) Q-Q distribution of residuals

图3为SRT、ST-RH和IDW 3种算法对南京站2017年12个月逐时气温观测资料进行质量控制NSC、MAE、RMSE三项性能指标分布情况。图3中ST-RH的MAE和RMSE的值很低，低于0.1，说明预测误差小；NSC的值很高，接近于1，说明预测值相对于实际观测值拟合程度很高。总地来看，ST-RH的三项性能指标值相对于SRT和IDW而言均表现出明显的优越性且其三项指标值的变化基本一致。SRT方法除了1月在绝大多数月份优于IDW方法，1月出现的不一致性与随机误差的分布有关。

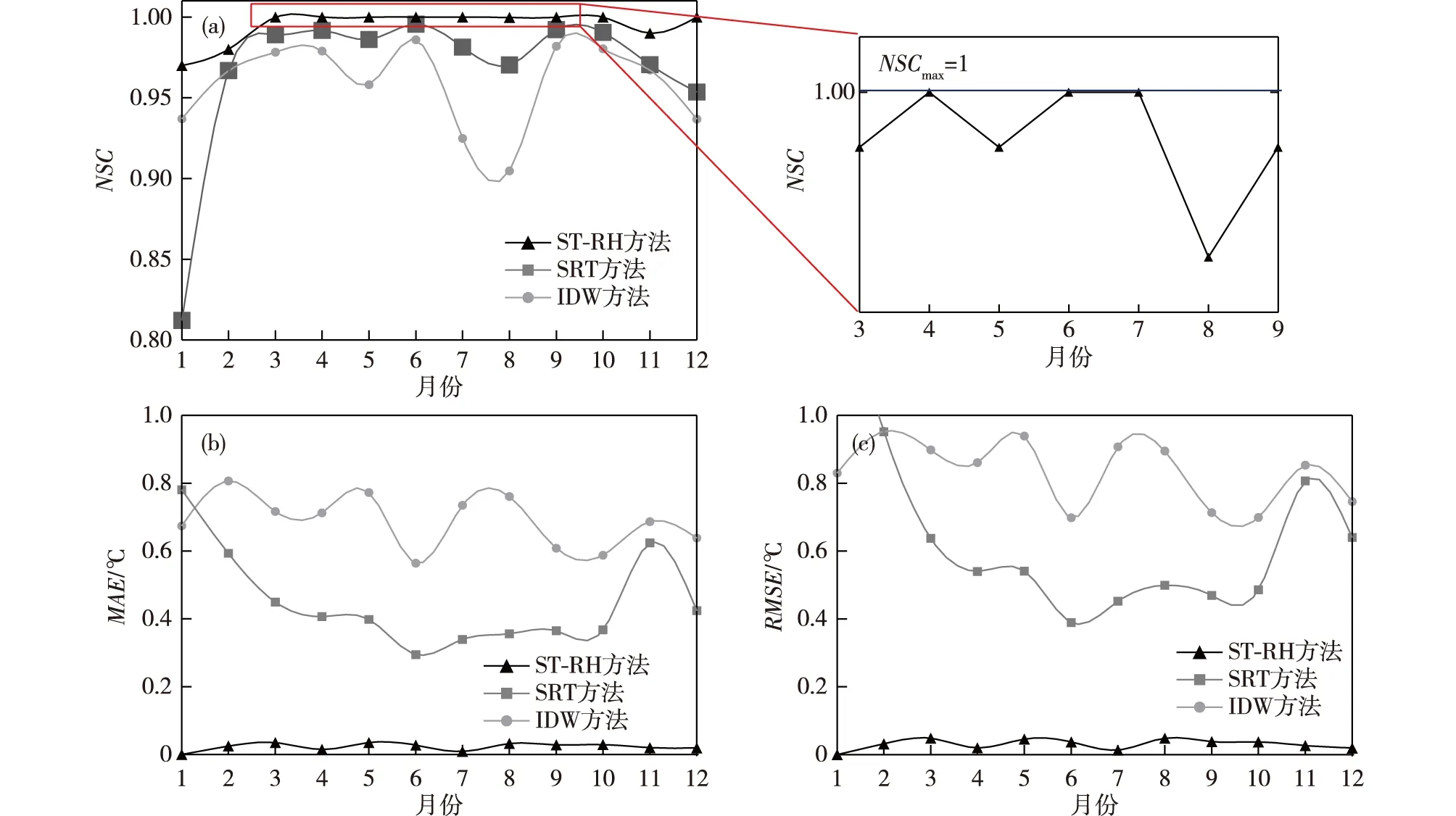
图3 ST-RH、SRT和IDW 3种算法对南京站2017年逐时气温观测资料质量控制性能指标对比分析：(a)NSC；(b)MAE；(c)RMSEFig.3 Performance of ST-RH、SRT and IDW methods for the quality control of surface observations for Nanjing station in July 2017: (a) NSC; (b) MAE; (c) RMSE

为了进一步考察ST-RH方法的普适性，利用ST-RH、SRT和IDW 3种算法对全国14个地面观测站2017年地面气温观测资料进行质量控制，MSR、NSC、MAE和RMSE分析结果如图5所示。从图4可以看到，东南部地区的质量控制效果较西北部要好，一方面由于东南地区经济较发达，台站分布较密集便于多站联网质量控制；另一方面西北地区的气候、地形地貌环境复杂多变，给质量控制带来了不确定因素较多。从图4中MSR、NSC、MAE、RMSE 4个指标综合分析，ST-RH算法在3种算法中表现最优，SRT算法要优于IDW算法。此外，ST-RH算法表现出了更好的稳定性，对不同的地区适应性更好。

图4 ST-RH、SRT和IDW 3种算法对14个不同地区2017年逐时气温观测资料质量控制性能指标对比对比分析：(a)MSR；(b)NSC；(c)MAE；(d)RMSEFig.4 Performance of ST-RH、SRT and IDW methods for the quality control of surface observations for 14 different areas in 2017: (a) MSR; (b) NSC; (c) MAE; (d) RMSE

图5 ST-RH、SRT和IDW 3种质量控制算法代价敏感性分析：(a)14个不同地区AUC值分布；(b)AUC值标准差分布Fig.5 Cost sensitivity analysis of ST-RH、SRT and IDW methods:(a) AUC for 14 different regions; (b) SD of AUC

此外，本文为了评估算法的代价敏感性，采用AUC值对ST-RH、SRT和IDW 3种算法进行分析。图5a为通过ST-RH、SRT和IDW 3种算法对全国14个地面观测站2017年地面气温观测资料进行质量控制后结果的AUC值，从数值上来看ST-RH、SRT和IDW 3种算法的AUC值在不同的地区均大于0.75，表示3种算法的质量控制均是有效的。但是，从图5a可明显看出ST-RH算法是优于其他两种算法的，有5个地区ST-RH算法的AUC值大于0.9，体现了ST-RH算法的优越性。同时，图5b展示了ST-RH、SRT和IDW 3种算法AUC值的标准差分布情况，可以看出改则、天池、酒泉、包头、伊春、四平和三亚的幅值跨度较大，反映了ST-RH、SRT和IDW 3种算法在这7个地区的质量控制效果具有较大差异。结合图4以及三种算法的构造机理分析，ST-RH方法通过把温度与相对湿度的强耦合关系为解释变量融入算法，可以提高质量控制算法在气候极端地区或周围邻站稀少地区的效果。

3 结论

本文发展了一种基于改进空间面板数据模型的地面气温观测资料质量控制算法(ST-RH算法)，并对全国14个不同地区的地面气温观测资料进行质量控制检测。为了对新算法进行评估，本文采用多个指标值对质量控制效果进行分析，并与IDW算法和SRT算法进行比较。试验表明，ST-RH质量控制算法能有效地标记出地面逐时气温观测资料中的存疑数据，相对于SRT算法和IDW算法而言具有较好的质量控制效果。通过多组独立案例试验可得到以下结论：

(1)ST-RH算法能够实现对我国地面气温观测资料进行质量控制，能够有效地甄别出存疑数据。ST-RH算法相比较IDW算法和SRT算法而言，具有更好的检错效果和稳定性，其原因在于ST-RH算法通过地面气温观测资料的时空相关性来进行回归预测的，同时考虑到相对湿度与气温之间的强耦合关系，将相对湿度作为解释变量融进算法之中，增强了ST-RH算法的内部稳定性。

(2)从不同地区的质量控制效果来看，ST-RH算法效果普遍具有较好的质控效果。在西部、北部地区，ST-RH、SRT和IDW 3种算法质量控制效果均有下降，不同算法的质量控制效果差异性也较大。其原因一方面复杂的地理环境造成的近地面大气分布的非平稳特征加大了质量控制的难度；另一方面我国的西部、北部地区存在地面气象观测站点稀少的现象，为质量控制算法提供的可参考邻站观测信息不足。