基于误差积分模糊控制的电力弹簧解耦控制策略

赵智忠，杨 志，赵世辉

（1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学河北省电磁场与电器可靠性重点实验室，天津300130）

0 引言

可再生能源固有的间歇性、波动性，会引起电 网 电 压 波 动、谐 波 污 染、频 率 闪 变 等 问 题[1]～[4]，发电量与用电量难以实时平衡[5]。香港大学的Shu Yuen（Ron）Hui团队将机械弹簧的原理对偶到电力 系 统 中，提 出 电 力 弹 簧（Electric Spring，ES）的概念[6]，形成一种缓解可再生能源发电波动性的新方法。电力弹簧与对电能质量不敏感的非关键负载串联组成智能负载，在发电量变化时，将电能的波动传递到非关键负载，从而保证关键负载的电压稳定，使用电量跟随发电量的变化而改变。现阶段，电力弹簧已经具有稳定电压、调节功率因数、频率管理、减少三相不平衡等多种功能[7]。

为应对可再生能源在电网渗透率逐渐提高的现状，文献[8]运用双闭环PI控制系统对电力弹簧进行控制，该控制器结构简单，但只能进行无功补偿。文献[9]运用相量图法推导出相角控制方法，采用比例谐振（PR）控制器，可以进行有功补偿，但须要采集大量电网参数，不利于实际应用。文献[10]设计了基于d-q分解的电流控制方法，可以同时实现母线电压稳定和功率因数校正的目标，但控制器结构复杂，调试难度大。文献[11]～[13]分别采用单纯型算法、免疫遗传算法、改进人工鱼群算法对原有的控制策略进行优化，均实现了一定程度的改进。

文献[14]将分数阶PIλDμ控制器应用到并网逆变器中，该控制器的灵活度更高，调节效果好，但是依然属于固定参数类型，无法根据系统的实时变化在线调节控制器的参数。文献[15]提出一种PI控制与卡尔曼滤波相结合的控制算法，该算法虽然可以自适应调整控制器参数，但是噪声矩阵存在一定误差，导致控制精度不高。文献[16]提出变初值模糊PI控制理论，该理论能够实时进行模糊推理，同时还能在线调整PI控制器参数初值。该理论比传统模糊PI控制更加先进，但是变初值的计算具有特异性，在应用于其他控制系统时，须要重新进行初值调整，增加了工作量。文献[17]将模糊PI控制理念引入到电力弹簧控制策略中，但控制策略存在动态响应慢、只能补偿无功功率的不足，无法适应电压波动幅度较大的情况。文献[18]，[19]采用变论域模糊控制对的PI控制器参数进行优化，但须要进行复杂的伸缩因子计算，且只能补偿无功。

目前，单独的PI控制器大多缺乏自适应性，而已有的电力弹簧模糊PI控制器只在可再生能源功率波动时进行无功补偿，未涉及有功补偿。本文提出了基于误差积分模糊控制的径向弦向解耦控制策略（RCD解耦控制策略）。运用相量法将电力弹簧电压分解为径向分量和弦向分量，分别控制智能负载的电压和功率因数，实现无功功率与有功功率的同时补偿。RCD解耦控制策略在调节关键负载电压时，具有无超调的特点，使以误差和误差变化率作为输入的传统模糊控制器难以发挥作用，当可再生能源出力剧烈变化时，传统模糊控制器在线调整PI参数往往达不到理想的效果。本文设计了一种以误差及误差积分为输入的新型模糊PI控制器，结合稳定关键负载电压的控制目标，制定了相应的模糊规则库。该控制器无需增加额外的计算量，可实现PI控制器参数的自适应调整。最后通过Matlab验证了所提控制策略的有效性。

1 电力弹簧的工作原理

电力弹簧在单相可再生能源并网系统的连接形式如图1所示。

图1 电力弹簧连接简图Fig.1 Connection diagram of electric spring

虚线框中的直流电源Vdc、LC滤波器、半桥逆变器组成电力弹簧基本拓扑结构。Ues为电力弹簧输出电压；Lf，Cf分别为LC滤波器的电感与电容；Znc为非关键负载阻抗；Uo为非关键负载电压；Zc为关键负载阻抗；Us为关键负载电压；I2为非关键负载的电流；RL，XL为输电线路阻抗；Ug为模拟分布式光伏并网的输出电压。

电力弹簧与非关键负载串联形成智能负载，一般将空调系统和加热系统等对电压不敏感的设备分类为非关键负载，将对电压敏感的设备分类为关键负载，其允许的工作电压范围较小，例如医用器械。

采用适当的控制策略可以使电力弹簧工作于容性模式、感性模式和阻性模式3种模式[20]。当母线电压低于参考值时，电力弹簧工作于容性模式，此时电压Ues滞后I290°，发出无功功率并稳定母线电压为参考值，将电压的波动传递到非关键负载，使其消耗的功率减小；当母线电压高于参考值时，电力弹簧工作于感性模式，此时电压Ues超前I290°，吸收无功功率并稳定母线电压为参考值，非关键负载消耗功率增加；当母线电压等于参考值时，电力弹簧不起作用，此时Ues与I2同向，称之为阻性模式。通过3种工作模式的切换，电力弹簧可以有效缓解由可再生能源并网引起的功率不平衡问题。

2 RCD解耦控制原理

RCD解耦控制算法因其结构简单、功能强大的特点，在现有控制策略中最易于实现。它巧妙的将电力弹簧电压分解为径向和弦向分量，使智能负载的功率因数和视在功率解耦[21]，在改善智能负载功率因数的同时降低风力或光伏发电随机性对关键负载电压的影响。由图1可得:

式 中:|Us|∠θs为 关 键 负 载 电 压；|Ues|∠θes为 电 力 弹簧电压；|Uo|∠θo为非关键负载电压。上述角度以及下文所提角度均以 θs为参考。

调节电力弹簧电压的大小和相位，可以使非关键负载电压的幅值|Uo|大于、等于或小于关键负载 电 压 幅 值|Us|。同 理，|Uo|∠θo的 相 位 也 可 以 超 前、滞后或等于|Us|∠θs。两种可能的电压相量关系图如图2所示。其中:φ1为非关键负载阻抗角；φs1为智能负载功率因数角。

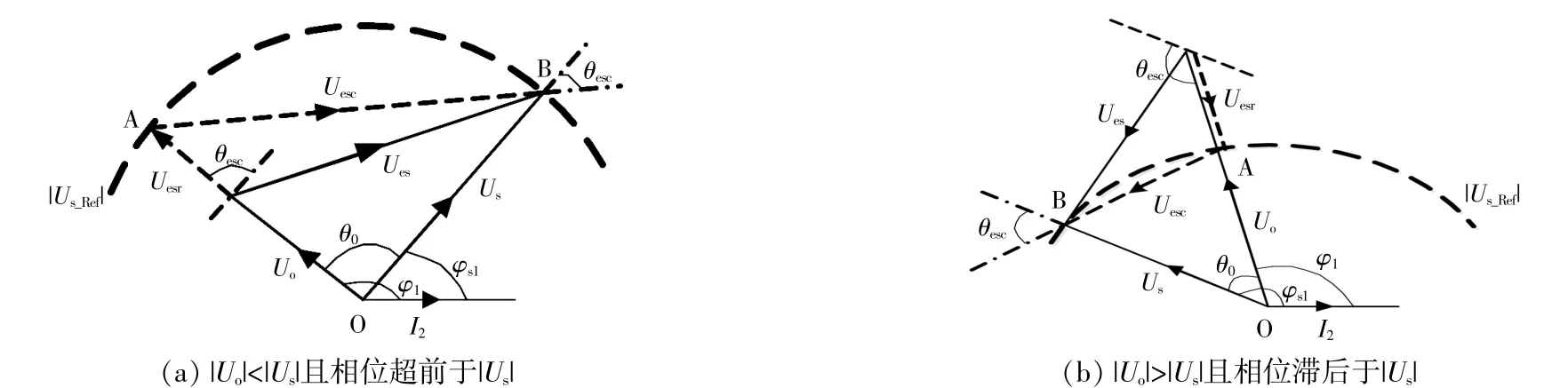
图2 电力弹簧电压分解Fig.2 Electric spring voltage decomposition

假设网络电压|Us|为定值，将电力弹簧电压|Ues|∠θes分 解 为 径 向、弦 向 分 量 为

式 中:|Uesr|，|Uesc|分 别 为 电 压|Ues|∠θes解 耦 后 的 径 向分量 与弦向 分量幅值；θesr，θesc分别 为径向 分量 和弦向分量的相位角，其参考相量为|Us|∠0o。

式（2）为RCD解耦控制理论核心思想，通过将电力弹簧电压分解，智能负载功率因数与关键负载电压得以解耦。

由 图2可 知，|Uesr|∠θesr可 以 与|Uo|∠θo同 向 或反向。θesr表达式为

|Uesr|表达式为

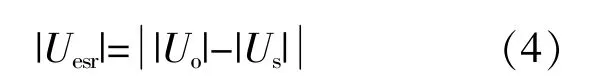
由 式（3），（4）可 知，径 向 电 压 分 量 的 相 角 只 与非关键负载的电压相位角有关，幅值与非关键负载电压以及母线电压相关。

由图2相量图可知，θesc和 θo均与△OAB有关。根据三角形内角和定理可以得到:

在△OAB中，运用余弦定理，可得|Uesc|为

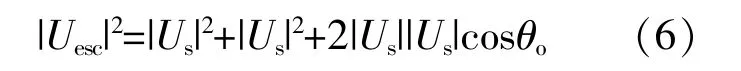
由 式（5），（6）可 知，弦 向 分 量 的 相 角 仅 与 非 关键负载电压相角有关，弦向分量幅值与母线电压及非关键负载电压相角有关。

RCD解耦控制框图如图3所示。

图3 RCD解耦控制框图Fig.3 RCD decoupling control block diagram

以上分析均假设|Us|为定值，在实际的控制系统设计中，只须给定 θo值和母线参考电压|Us_Ref|，则可根据式（3）～（6）计算电力弹簧电压的弦向分量和径向分量，实现智能负载功率因数与电压的解耦控制。

3 模糊控制器设计

3.1 新型模糊控制器

传统的模糊PI控制器大多采用误差和误差变化率作为输入[22]，然后基于这两种输入制定对应的模糊控制规则，输出比例增益Kp和积分增益Ki的修正量[23]，其控制效果多表现为减少超调量和动态响应时间[24]～[26]。而RCD解耦控制特有的算法特点，使其在调节过程中不存在超调量，且动态响应时间快于已有的几种主流电力弹簧控制策略。传统模糊控制器应用于RCD解耦控制策略时调节效果不明显，几乎没有改进。

另一方面，当可再生能源输出电压波动范围较大时，传统模糊控制器也很难对母线电压进行有效调节。超调量的消失使得系统调节初期的振荡过程减弱，误差变化率将很快减小甚至趋于0。在不存在超调量的情况下，当母线电压远高于参考值时，Kp会由于模糊控制的作用而减小，从而增大动态响应时间，Ki的小幅变化对系统稳态误差的影响微乎其微，当母线电压远低于参考值时，虽然模糊控制的作用会使Kp增大从而加快动态响应，但在RCD解耦控制的背景下这种改进并不明显，且Ki的减小会使系统的稳态误差增大。

考虑到上述问题，以及RCD解耦控制算法在实际应用过程中无超调且动态响应快的特点，本文提出一种采用误差及具有记忆功能的误差积分作为输入的模糊控制器，制定以稳定关键负载电压为目标的控制规则，输出量仍然是Kp和Ki的修正量，控制器结构如图4所示。

图4 模糊控制器结构图Fig.4 Structure diagram of fuzzy controller

传统的模糊控制着眼于改善系统的动态过程，而提出的误差积分模糊控制器则以稳态调节为重点。当可再生能源并网后，输出电压波动程度不同时，对PI控制器参数的要求也不同。在系统调节前期，设定PI控制器参数的初值，这里设置的初值相对较小，ΔKp和 ΔKi均为正，通过对初值向上调节自适应地调节Kp和Ki。在调节进入中后期时误差大幅减小，而误差积分具有记忆功能，可根据先前系统电压偏离参考值的程度继续维持模糊控制器的输出，保证系统后续调节的准确性，最大限度地降低光伏或风电并网引起的电压偏移。

3.2 模糊控制器设计

模糊控制器采用双输入双输出的二维形式，输入为关键负载电压与参考值的误差以及误差相对于系统运行时间的积分，输出为 ΔKp和 ΔKi，则PI控制器实际参数为

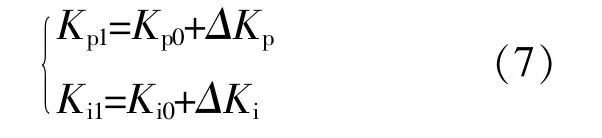
式中:Kp0和Ki0为PI控制器参数初始值；Kp1和Ki1为调节后的实际值。

考虑到实际运行中电力系统电压波动情况以及后续仿真实验的设计，误差e（t）的论域取为{0，10}，在不同电压波动情况下，计算误差积分的取值范围，经过综合比较，量化因子为3。ΔKp的论域取为{0，10}，比例因子为4。ΔKi的论域取为{0，10}，比 例 因 子 为4。

三角形隶属函数表达式简单，对输入的变化反应灵敏，故将其设置为上述模糊变量的隶属函数。采用Mamdani型推理算法，去模糊化方法采用重心法，得到的模糊控制规则库如表1和表2所示。

表1 ΔKp控制规则Table 1ΔKp control rules

表2 ΔKi控制规则Table 2ΔKi control rules

续表2

由表1，2可以看出，当误差与误差积分取值较大或较小时，模糊控制器的输出也会随之增加或减小。当系统经过调节初期的过渡使控制器的误差输入一直保持很小时，积分环节由于存在对于系统先前误差状态的记忆作用而没有减小，可以继续使控制器保持较大的输出。

4 仿真验证

本文在Matlab/Simulink软件中搭建了如图1所示的仿真模型，对所提模糊控制器的有效性进行验证。使用恒压源模拟可再生能源并网，电力弹簧采用直流侧带直流电压源的ES-2结构，具体网络参数如表3所示。

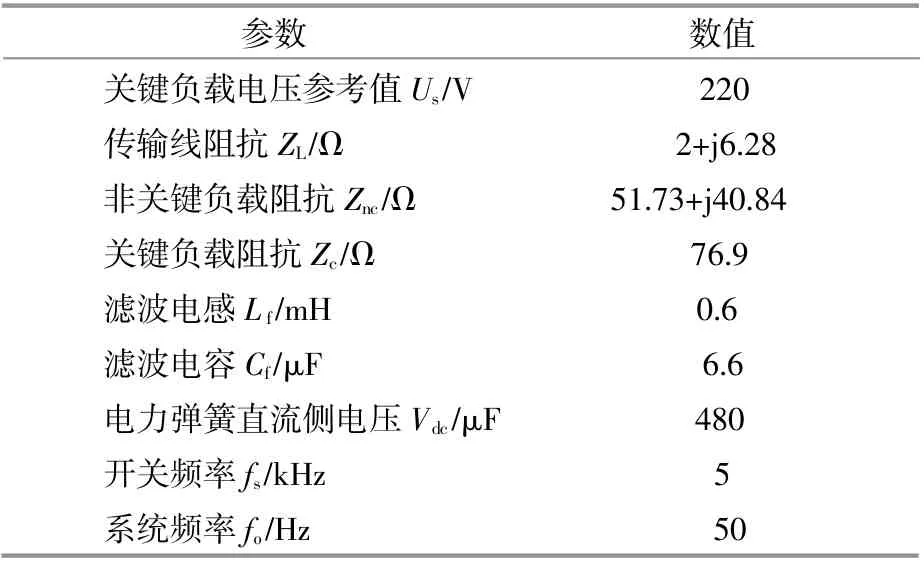
表3 仿真模型网络参数Table 3 Simulation model network parameters

仿真设计为3组对比实验，分别使用普通PI控制器、传统模糊控制器和提出的模糊控制器。当关键负载电压为220 V时，根据网络参数计算出此时电源侧电压为347.67 V。在随后的仿真实验中 ， 将 电 压 源 分 别 设 置 为331.67，340.67，353.67，363.67 V 4个电压等级，其中340.67 V，353.67 V模拟可再生能源电压小幅波动的情况，331.67 V，363.67 V模拟可再生能源电压大幅波动的情况。在上述4个电压等级下，测量3组仿真母线电压变化情况。

4.1 电压小幅波动仿真分析

可再生能源电压波动较小时关键负载电压绝对值曲线如图5，6所示。

图5 电源为340.67 V时3组仿真母线电压对比Fig.5 Comparison of three sets of simulated bus voltages when the power supply is 340.67 V

图6 电源为353.67 V时3组仿真母线电压对比Fig.6 Comparison of three sets of simulated bus voltages when the power supply is 353.67 V

在仿真开始阶段，由于风速或光照变化，关键负载电压偏离参考值±4 V。0.25 s，电力弹簧投入运行，在电压波动较小的情况下，3种控制方法均可以实现快速的动态响应，使关键负载电压在0.05 s内稳定到参考值附近。传统模糊控制在调节初期比普通PI控制更加接近参考值，但是后续调节效果不理想。本文提出的误差积分模糊控制不仅动态响应快，并且由于微小误差的持续存在，误差积分得以不断的变化，从而实时调整PI控制器参数，加强后续调节的比例与积分作用，使关键负载电压更加逼近参考值。

4.2 电压大幅波动仿真分析

可再生能源电压波动较大时，关键负载电压绝对值曲线如图7，8所示。

图7 电源为331.67 V时3组仿真母线电压对比Fig.7 Comparison of three sets of simulated bus voltages when the power supply is 331.67 V

图8 电源为363.67 V时3组仿真母线电压对比Fig.8 Comparison of three sets of simulated bus voltages when the power supply is 363.67 V

初始阶段，关键负载电压偏离±10 V。0.25 s，投入电力弹簧，普通PI控制和传统模糊控制均无法实现控制目标，存在较大稳态误差。本文控制策略下，母线电压在0.25 s后迅速接近参考值，稳态误差只有0.25 V。后续过程中，误差积分依然保持较大，且处于动态变化中，实现PI控制器积分作用和比例作用的强弱跟随可再生能源电压波动幅度的大小来变化。

4.3 电压连续波动仿真分析

将仿真时间设置为10 s，按347.67，340.67，353.67，331.67，363.67 V的 顺 序，每 隔2 s切 换 一次电源电压，模拟可再生能源输出的连续波动，得到的关键负载电压绝对值曲线如图9所示。

图9 电源电压连续波动关键负载电压对比Fig.9 Comparison of critical load voltages with continuous fluctuations in power supply voltage

当电源电压为347.67 V时，电力弹簧电压弦向分量调节智能负载的功率因数cosφ1，使得关键负载电压小幅偏离参考值。在2 s时电源电压产生波动且波动范围逐渐增大，3种控制方法在电压波动较小时均可以将关键负载电压稳定在参考值附近。但是随着电压波动范围增大，普通PI控制和传统模糊控制调节效果不佳，关键负载电压与参考值存在较大误差，而本文提出的模糊控制器调节效果明显优于上述两种控制方法。

cosφ1，Ues以 及Uo的 仿 真 结 果 分 别 如 图10～12所示。

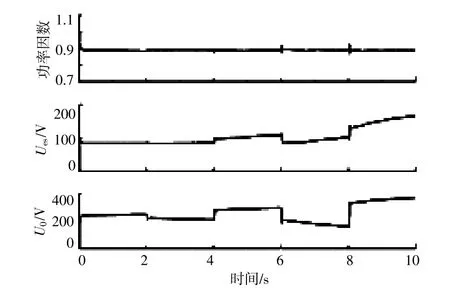
图10 普通PI控制仿真结果Fig.10 Common PI control simulation results

图11 传统模糊控制仿真结果Fig.11 Traditional fuzzy control simulation results

图12 本文提出的模糊控制仿真结果Fig.12 The proposed fuzzy control simulation results

当电力弹簧未投入时，智能负载功率因数为0.785，电力弹簧投入后，由图2相量图计算可得，此时智能负载功率因数为0.88。由图10～12可以看出，在整个仿真运行过程中，智能负载功率因数均稳定在0.88左右，与理论计算基本吻合。当电源电压切换时，Ues在普通PI控制和传统模糊控制条件下均存在不同程度的跳变，造成控制器调节精度降低，稳定性下降。而模糊控制器在不同电压工况下均可以使电力弹簧输出相对稳定的电压，具有较强的鲁棒性，并且随着电源电压的波动范围增大，电力弹簧的输出也相应增加，保证调节精度。Uo在3种控制策略下均可以实现自身电压的“压缩”和“拉伸”，减少自身功率消耗或消纳多余功率。但在提出的模糊控制条件下，Uo的变化幅度更大，拉伸效应明显，对于母线电压具有更强的支撑能力。

5 结论

针对电力弹簧RCD解耦控制无法实时调节PI控制器参数，且传统模糊控制器不能发挥应有作用的问题，本文提出了以误差和误差积分作为输入的新型模糊控制器，并制定了相应的模糊控制规则库。由于积分环节的记忆作用，控制器在可再生能源输出电压波动时会根据调整前的误差情况，输出对应的PI控制器参数修正量以达到稳压目的。仿真结果表明，所提出的控制器调节效果优于已有控制方法，可以有效应用于RCD解耦控制策略中，且在电压波动幅度不同时均可实现控制目标，为解决可再生能源并网所引起的电能质量问题提供了新思路。