在深度学习中培养学生高阶思维
胡金锦


在高中信息技术教学中,以项目为基础,通过深度学习,可以培养学生的高阶思维能力。高阶思维是高阶能力的核心,主要指问题求解能力、批判性思维能力和创新应用能力。浙江省在信息技术选考试题中,力求依托真实情境,考查学生在真实情境中分析问题、综合运用知识解决问题的能力,问题的解决需要学生从深度学习中获得分析、综合应用、解决问题、迭代优化的能力,而项目学习为深度学习提供了极佳的平台和途径。下面,笔者以“‘蒲丰实验算法实现”项目学习为例,说明深度学习在促进学生高阶思维发展中的应用。
● 基于复杂的情境,培养学生问题求解能力
高阶思维的活动对象是非结构化、真实而复杂的情境,在项目设计时,要尽可能提供一些富有挑战性的开放的现实问题,以知识情境化来实现知识问题化。同时,也要把握好项目的规模与难度。例如,在“‘蒲丰实验算法实现”项目中,笔者通过如下一段史料,引出项目主题——用计算机模拟投针验证蒲丰投针实验,同时,界定此项目采用随机数即蒙特卡罗法证明pi,通过统计分析让学生体验随机现象中隐藏的确定性,为后续大数据、人工智能的学习做引子。
1777年的一天晚上法国数学家蒲丰先生的家里宾客满堂,原来他们是被邀请来见证一个神奇的实验——地上放着一张纸,纸上画着等间距的平行线(间距D=1),宾客们一轮一轮往纸上随机投针(针长L=1/2D),蒲丰先生在一旁记录。如此忙碌了一个小时,蒲丰先生宣布结果:“大家一共投针2212次,与线相交704次,相除结果正好是3.14。”蒲丰提高嗓门说这正好是“pi的近似值”,宾客们一片哗然,纷纷议论。
接下来,学生在教师的引导下,通过“抽象建模、算法设计、程序实现、调试优化”等步骤循序渐进地构建问题处理的有序思维。
第一步:抽象与建模
(1)提炼核心要素加以确定。让学生从数学角度分析针与并行线相交的因素,如下页图1所示。
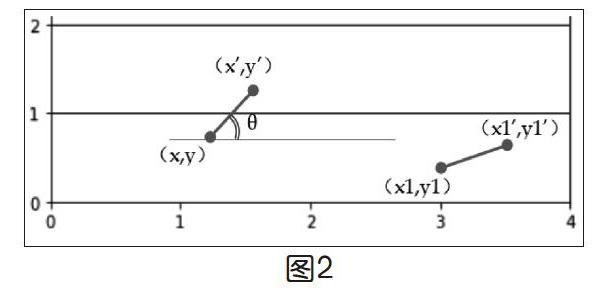
在提炼核心要素的环节,通过问题串的形式分解问题,降低问题复杂性与思维难度,如通过“如何确定针在平面中的位置”和“如何判断针与线是否相交”问题串引导学生提炼核心要素。在交流分析中,要素不断得以明确,大家发现针的位置可以通过两端坐标(x,y),(x',y')或一个端点坐标(x,y)和水平方向的夹角θ来确定。针与线的相交可以通过判断y与y'是否处于不同的区间实现,如图2所示。而方案二程序实现较为简单,确定关键要素:纵坐标与夹角(y,θ)。
(2)使用数学符号描述解决问题的计算模型。由图2可知D=1则针长为1/2,则y'=y+0.5×sinθ。与平行线是否相交需考虑纵坐标y与y'是否落在同一区间内,如图2中y落在区间(0,1),y'落在区间[1,2),或y正好落在线上(y=1),则针与并行线相交,反之不相交。
基于上述分析,可以得出解决该问题的计算模型,如图3所示。
第二步:设计算法
算法设计是人机适配的过程,需要将问题解决过程流程化,并按计算机处理问题的形式进行分解与明确化。引导学生采用“自顶向下,逐步细化”的策略,迭代的思想将问题的求解步骤进行反复梳理细化成最终的算法:①输入模拟投针次数n;②投针计数器i,初始化为1;③若i≤n,则转④,否则转⑧;④随机产生y[0,10000]坐标;⑤随机产生与x轴的夹角θ(0≤<360°);⑥当y+1/2sinθ」不等于y」或y」等于y,m=m+1;⑦i增加1,转③;⑧pi=n/m,输出pi。
第三步:算法实现与调试
高一的学生刚刚接触编程,程序实现能力较弱,因此可以通过流程图,引导学生梳理算法思想,进一步细化算法步骤,使执行过程更加清晰化、明确化,如图4所示。
学生经历了抽象建模、算法设计、程序实现及调试这一计算机解决问题的完整过程,了解到解决问题的起点是明确问题,算法的形成过程是自顶向下不断迭代的过程。
● 通过反思与改进,培养学生批判性思维能力
算法的实现过程是一个“尝试—验证—修正—再尝试”不断迭代、不断优化的过程。在对算法不断反思、评价与改进的过程中,势必引发学生对问题的深入思考,这对培养学生科学严谨的学习态度,勇于探究、勤于思考的高阶思维品质有着积极的意义。在模拟随机投针项目教学中,项目小组对上一步的模拟投针实验程序提出了以下几方面的质疑,并进行了多维度的验证。
1.模拟投针实验程序中含有π,存在结论证明结论的问题
细心的学生发现在程序中使用了常量math.pi(π)即存在结论证明结论的逻辑,好像不适合,通过网上查阅相关文献发现也存在类似的问题,原因是Python三角函数采用的是弧度制。通过分组学习探究,学生给出的解决方案是多样化的,下面引用几种比较典型的改进策略。
改進一:采用角度随机数替换弧度随机数。
在程序改进过程中,有的小组通过查阅相关资料,在浙教版《数据与计算》中第85页的“math模块中常用常数与函数”表中找到了math.radians(x)函数,将弧度随机数改成了角度随机数,程序改进如下页图5所示。
改进二:采用随机斜率k代替弧度。
产生随机数坐标(a,b),a∈[-1,1],b∈[-1,1],得到随机斜率。设针长为l,一端坐标为(x1,y1),另一端坐标为(x2,y2),得:(q>0),得到y2=y1+aq,x2=x1+bq,于是l2=(x2-x1)2+(y2-y1)2=(a2+b2)q2,q=,,,程序中只需考虑y2即可,改进的部分代码如下页图6所示。
2.增加投针次数是否能使实验结果更加逼近3.14
学生容易想到的是将上一步的代码封装为pi(k)函数,即使用列表记录不同k值下的抛针结果值pi(k),并使用matplotlib将结果可视化,代码略,程序执行结果如图7所示。
● 开展追求本质的深度学习,培养学生创新应用的能力
在验证增加投针次数是否能消除随机不确定性,使实验结果逼近3.14的问题时,由于需要重复调用投针pi子程序,程序的执行效率为O(n2),随着运行规模的增加,程序执行时间成倍增长,效率越来越低下。此时就引出了能否将程序优化为O(n)的问题。在项目分组实施的过程中,得到了两种比较典型的优化策略。
优化方案一:分组抛针求平均概率法——以抛针1000枚为一组,计算多组平均概率(代码略)。
优化方案二:一边抛针一边统计计算pi值,代码如下页图8所示。
在算法的改进过程中,不同层次的学生选择了不同的优化策略,学生在各自的思维层次得到了充分的发展。在项目教学实施的过程中,还可以提出改进型问题拓展。例如,验证完整的蒲丰公式pi=2l*n/(m*D),还可以引导部分学习基础较好的学生实现抛针过程可视化。
模拟投针的问题模型类似于蒙特卡洛方法求解pi值,可以引导学生将蒙特卡洛算法迁移至新的问题情境中,如使用投点比例来算π值、求定积分或利用随机数解方程等。
依托真实情境的项目教学,为学生提供了高阶思维实践的载体与空间,在项目主题的生成性发展过程中,还能促进学生发现问题并不断改进和优化算法的能力,并将问题解决的过程与方法移到与之相关的其他问题解决中。在此过程中,学生的思维经历了解构到重构的过程,他们对信息的敏感性、对知识的掌控力、对问题求解的思考力得到了充分的发展,高阶思维能力得到了最大程度的提升。

