国外有轨电车小半径曲线轮轨动力学及减磨优化分析

廖 涛，徐井芒，周文涛，王小韬，王 建

（1. 西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031；2. 中铁二院工程集团有限责任公司，四川成都 610031）

1 研究背景

在山地城市线路条件下，由于线路等级低、沿途坡度大、曲线半径小、弯道多等原因，轮轨磨耗的问题更为突出，在这种条件下的轮轨关系、磨耗标准程度没有相关研究资料，还没有相关学者对这一课题进行深入研究。研究山地城市低地板车辆动力学是一项艰难的任务，在直线轨道以较低速度运行时，会产生摇摆问题，速度较高时，可能出现激烈的蛇行或浮沉振动现象[1]。当列车通过曲线时，车轮可能爬行，产生过大横向力，造成钢轨外翻。轮轨间的磨耗始终是研究轮轨关系的核心问题，长期制约着轨道交通运输的发展，国内外学者对此进行了大量研究，但目前鲜有针对海外山地城市低地板车辆的轮轨磨耗研究，国内外学者对轮轨磨耗的研究主要限于普速铁路车辆、高速铁路车辆、重载铁路车辆和地铁车辆等对象[2-5]。

在此背景下，本研究综合运用车辆-轨道系统耦合动力学、轮轨滚动接触理论及轮轨磨耗模型等理论，以保证车辆运行的安全性、稳定性、平稳性和减小轮轨磨耗、延长轮轨使用寿命为目的，运用SIMPACK软件建立车辆-轨道系统动力学模型，研究曲线半径、轮轨摩擦系数、车辆轮重、车辆通过速度等参数对轮轨动力学和磨耗的影响规律，以期指导轨道结构的优化设计、养护维修，并对山地城市线路运行条件下的轮轨磨耗控制提供参考。

2 计算模型

2.1 模型概况

目前，国内外鲜有文章针对长大坡道、小半径、大运量的有轨电车轮轨关系分析研究。本文结合埃塞俄比亚有轨电车项目，基于低地板有轨电车结构特性和轮轨关系建立对应的非线性嵌入式轨道车线耦合动力学模型，计算了不同曲线半径、轮轨摩擦系数、车辆轮重、车辆通过速度等参数对钢轨磨耗的影响规律。

埃塞俄比亚首都——亚的斯亚贝巴的有轨电车项目具有大坡道、小半径、高运量的特点和运营条件，该低地板有轨电车项目是全世界第一个最大坡度达55‰、最小半径为50 m、日运量约达12万人次、行车条件恶劣的山地城市有轨电车项目。

埃塞俄比亚有轨电车线路条件多为大坡度、小半径地段，钢轨形式为50轨，运营列车为70%低地板有轨电车，3节列车编组，中间的短车体采用车轮可以独立旋转的非动力转向架，两侧长车体下采用传统的动力转向架，列车采用接触网供电方式。

2.2 车辆动力学子模型

本文基于车辆-轨道耦合动力学理论[6]，利用多体系统动力学仿真软件SIMPACK建立用于计算分析轮轨磨耗程度的车辆-轨道系统动力学模型，该模型包括车辆动力学子模型和轨道动力学子模型，两个子模型之间通过轮轨接触关系连接[7]。

车辆动力学子模型采用埃塞俄比亚70%低地板轻轨车整车系统，由3节车体铰接而成，整车系统包括车体、构架、传统轮对和轴桥，均考虑伸缩、横移、浮沉、侧滚、点头和摇头6个自由度，系统共计84个自由度。车间悬挂包括铰接和车间减振器；二系悬挂包括二系钢簧、牵引拉杆、抗侧滚扭杆、横向止挡、横向减振器、垂向减振器等；一系悬挂为一系钢簧与止挡。车辆动力学子模型的主要建模参数如表1所示。

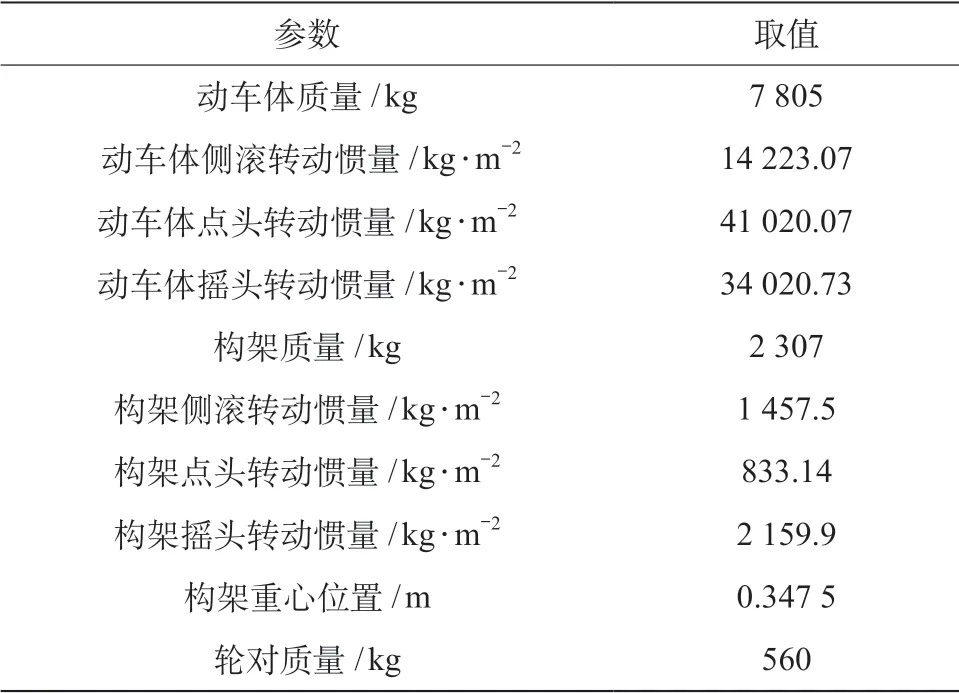
表1 车辆动力学子模型主要建模参数表

图1为车辆模型侧视结构拓扑图，描述了列车各部件之间的主要连接方式与相对运动关系。

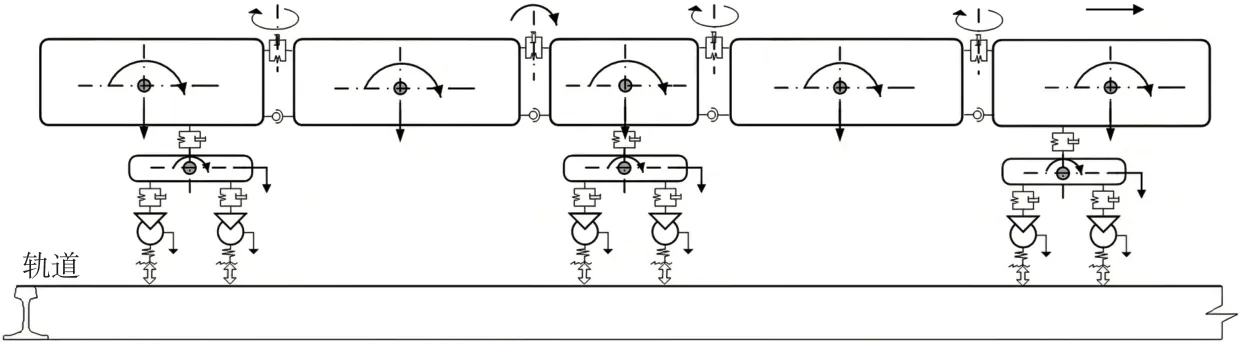
图1 列车模型侧视结构图

2.3 轨道动力学子模型

轨道动力学子模型采用无扣件嵌入式轨道形式，主要由槽型钢轨、轨道板组成，整体放入自密实混凝土层中。考虑轨道结构与特性进行模型建立[8]：轨下基础质量大且轨道板和路基之间几乎没有弹性，因此嵌入式轨道的振动主要体现在钢轨振动之上；轨道为连续支撑方式，钢轨简化为考虑垂向、横向、扭转自由度的铁木辛柯梁[9]。轨道动力学子模型的主要建模参数如表2所示[10]。

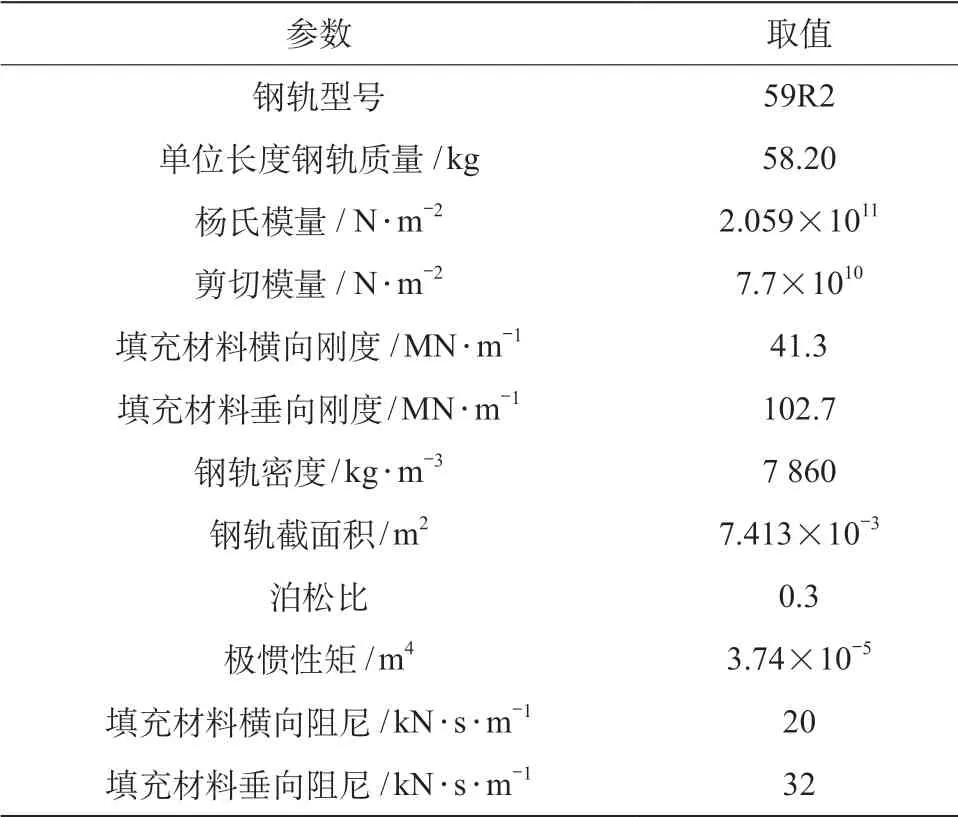
表2 轨道动力学子模型主要建模参数表

2.4 嵌入式轨道车线耦合动力学模型

通过轮轨关系将上述2个子模型连接，实现车辆-轨道耦合，更为准确地计算轮轨动力学与轮轨磨耗。各车轮的横向力、垂向力由低地板有轨电车模型输出，作为输入量导入嵌入式轨道车线耦合动力学模型计算钢轨横向、垂向、扭转响应，采用显式积分方法进行计算。之后将轨道动力学模块得到的钢轨位移作为输入，叠加轨道激励后进行下一步积分计算。

3 模拟计算结果分析

3.1 曲线半径影响分析

本小节计算了埃塞俄比亚有轨电车通过不同小半径曲线（R50 m，R200 m）时的各项动力学指标，计算结果如图2所示。

不同曲线半径下左右车轮的轮轨横向力如图2a所示。由图可知，曲线半径的改变对左轮影响较为显著，对右轮影响不大。左右车轮轮轨横向力峰值均出现在10 s附近，其中在50 m和200 m曲线半径的情况下，左轮横向力的峰值分别为21.45 kN、22.75 kN，右轮横向力峰值则分别为15.43 kN、17.94 kN。随着半径的增大，左、右车轮横向力除峰值处外均有不同程度的下降。两侧轮轨横向力在22 s以后，基本保持稳定；左侧轮轨横向力随着时间的增加而略微减小。

不同曲线半径下左右车轮的轮轨垂向力如图2b所示。由图可知，曲线半径的改变，对左右侧轮轨垂向力的影响均较大。其中，左侧钢轨处于增载状态，右侧钢轨处于减载状态，且半径越小，左右轮间垂向力差值越大。当曲线半径由50 m变化至200 m后，左右两侧轮轨垂向力分别呈现一定程度的减小和增大。图2b中，两侧车轮的轮轨垂向力具有较为明显的对称分布形式，且不论曲线半径大小，两侧车轮垂向力之和在时域范围具有稳定性。在50 m和200 m曲线半径下，左侧车轮轮轨垂向力峰值分别为62.5 kN、53.62 kN，右侧车轮轮轨垂向力峰值分别为55.49 kN、52.5 kN，均在相关标准规定的限度值范围内。半径从50 m增大到100 m时的轮轨垂向力变化明显。

不同曲线半径下左右车轮的磨耗功如图2c所示。由图可知，曲线半径虽然不同，但磨耗功变化规律基本一致，首先随时间的增大而增加，并在10 s附近陡增并产生峰值，然后回落并保持在某一值附近产生小范围波动，最后均缓慢减小。当曲线半径由50 m增大至200 m后，左右两侧车轮的磨耗功均减小，但左侧减小更明显。在50 m和200 m半径曲线下，左侧车轮磨耗功峰值分别为19.15 kW、2.97 kW，右侧车轮磨耗功峰值分别为5.89 kW、1.29 kW。

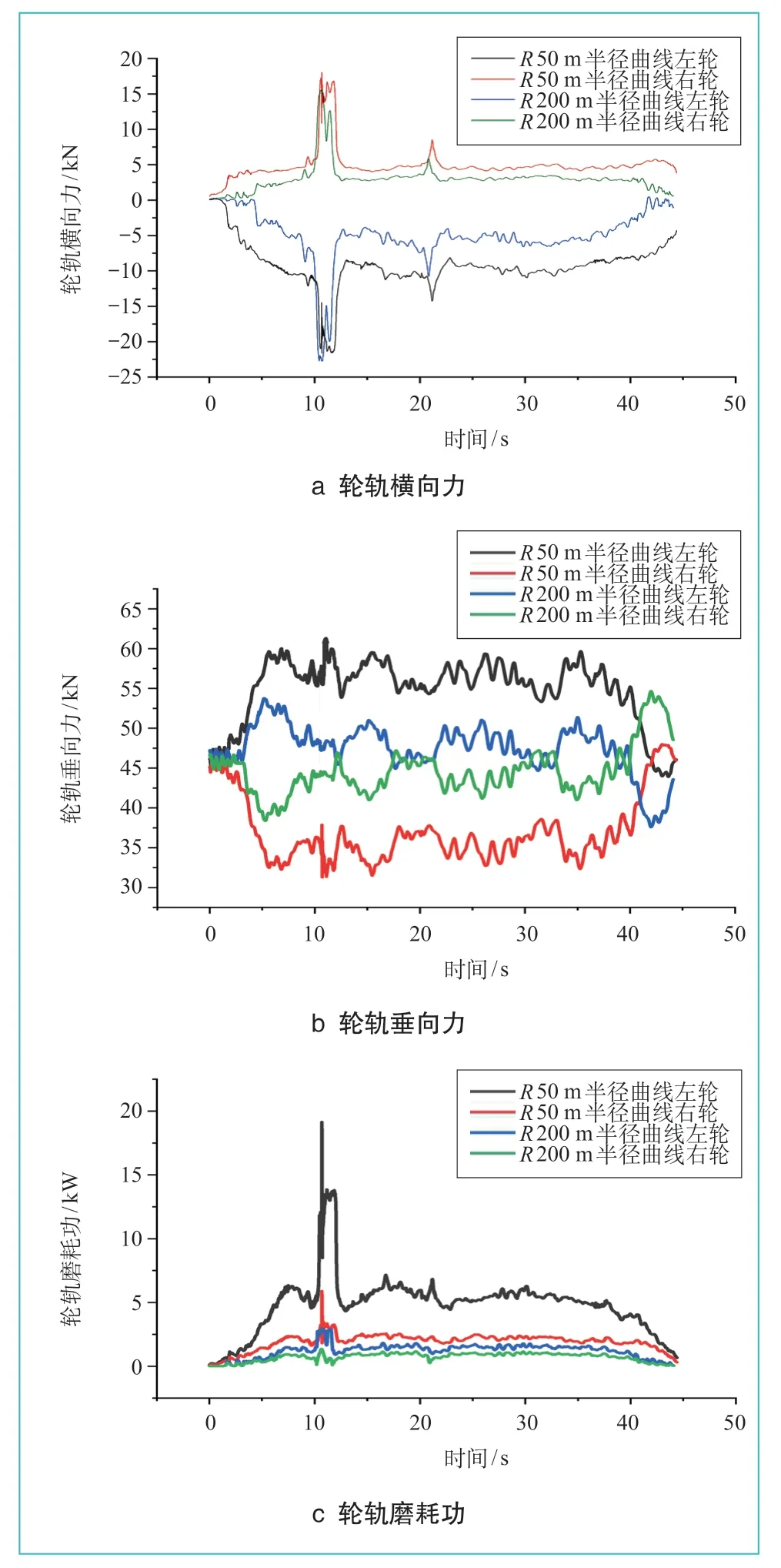
图2 不同曲线半径下动力学指标计算结果

3.2 轮轨摩擦系数控制

本小节计算了埃塞俄比亚有轨电车通过50 m半径曲线，摩擦系数分别为0.1、0.3时的各项动力学性能指标，计算结果如图3所示。

不同摩擦系数下的轮轨横向力如图3a所示。由图可知，摩擦系数的改变对轮轨横向力的影响较大。随摩擦系数的增大，右侧车轮的横向力曲线除特定位置外改变幅度较小。摩擦系数由0.1增大到0.3的过程中，左轮及右轮的横向力最大值均出现在10 s左右，左轮最大值为24.82 kN，右轮最大值为23.11 kN，在20 s时有小范围的增长，显然摩擦系数越小左右轮所受轮轨横向力峰值越大，且左轮横向力增大幅度大于右轮，建议在相关标准规定的限度值范围内适当增大摩擦系数。

不同摩擦系数下的轮轨垂向力如图3b所示。由图可知，不同摩擦系数下的左右轮垂向力均具有明显的对称性，左侧钢轨处于增载状态、右侧钢轨处于减载状态；随摩擦系数增大，左侧轮轨垂向力逐渐增大，右侧轮轨垂向力逐渐减小；在40 s及以前，左侧轮轨垂向力始终大于右侧。摩擦系数由0.1增大到0.3的过程中，左侧轮轨力最大值分别是57.35 kN、59.446 kN，均在相关标准规定的限度值范围内。显然摩擦系数越大，左轮承受的轮轨垂向力越大。

不同摩擦系数下的轮轨磨耗功如图3c所示。由图可知，不同摩擦系数下的左右车轮磨耗功均表现有类似规律，约在10 s位置产生磨耗功最大值；其余位置表现有相同的波动趋势，且在相同摩擦系数下左侧轮轨磨耗功明显大于右侧轮轨。随摩擦系数增大，磨耗功均呈增长趋势，右侧轮轨磨耗功增幅小于左侧轮轨磨耗功，需要指出的是，左侧车轮在摩擦系数为0.3时，其磨耗功远远大于摩擦系数为0.1时的磨耗功。

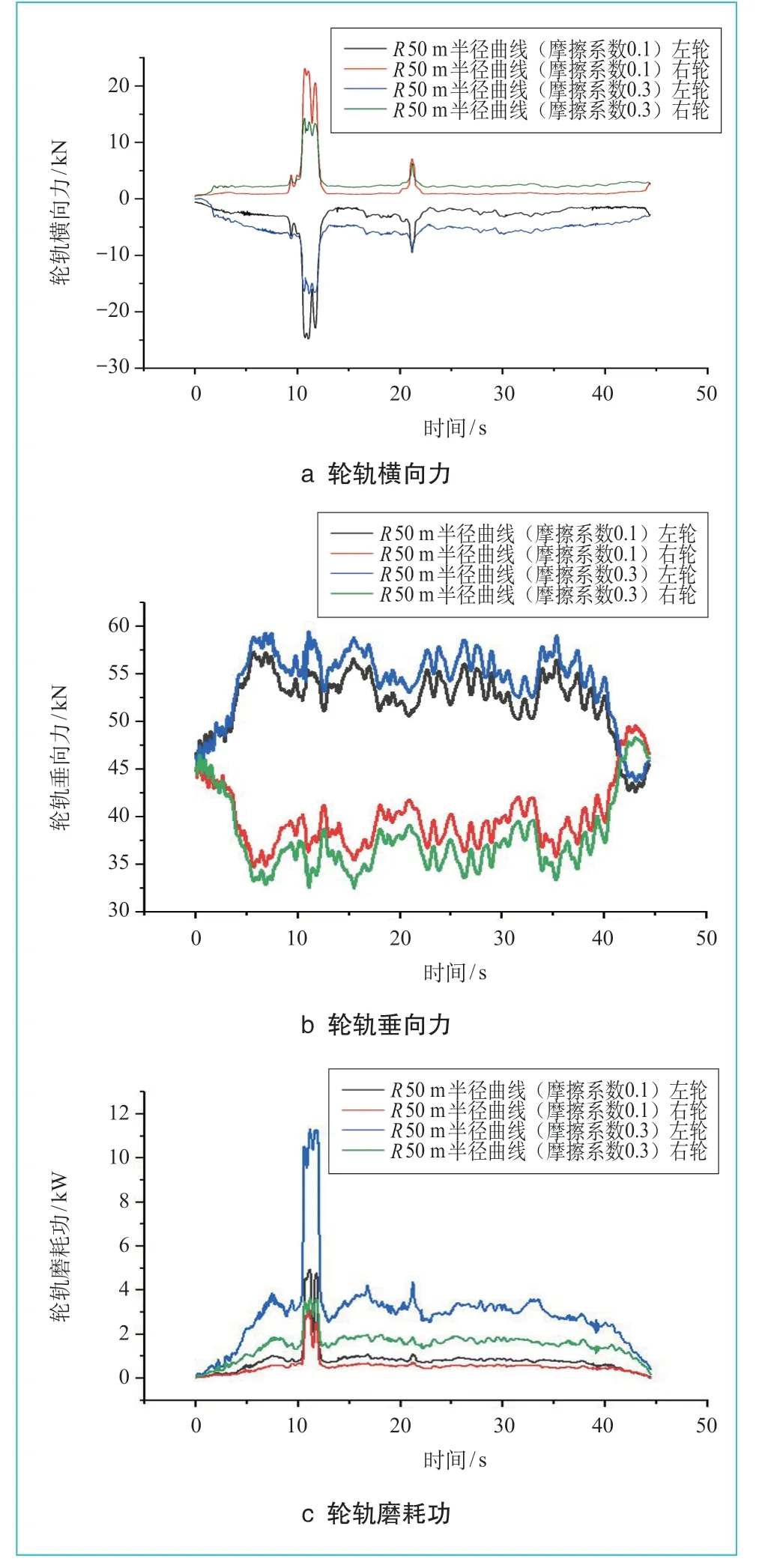
图3 不同摩擦系数下动力学指标计算结果

3.3 通过总重控制

本小节计算了埃塞俄比亚有轨电车的静轮重分别为32 kN、46 kN时的各项动力学性能指标，计算结果如图 4所示。

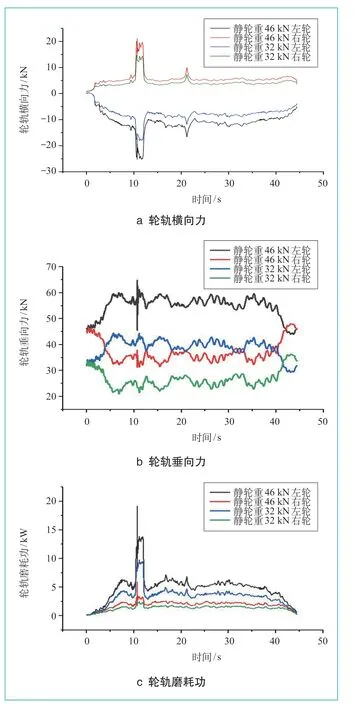
图4 不同静轮重下动力学指标计算结果

不同静轮重下的轮轨横向力如图4a所示。由图可知，不同静轮重下的左右轮轨横向力分布均具有较为明显的对称性。随静轮重增大，左右车轮轮轨横向力均有明显的增大。在10～15 s范围内，左轮横向力和右轮横向力增幅明显，其中左轮轮轨横向力峰值达到25.25 kN，右轮轮轨横向力峰值达到21.05 kN，由此可以看出，增加静轮重将会导致轮轨横向力的增大。

不同静轮重下的轮轨垂向力如图4b所示。由图可知，不同静轮重下的左右轮垂向力均具有明显的对称性，对称轴分别大致为32 kN和46 kN。左侧钢轨处于增载状态，右侧钢轨则处于减载状态。当静轮重由32 kN增大到46 kN后，左右侧车轮的轮轨垂向力均有比较明显的增大。其中，左侧车轮轮轨垂向力在同一静轮重下始终大于右侧车轮。静轮重为46 kN时左侧车轮在10 s处达到峰值64.813 kN。

不同静轮重下的轮轨磨耗功如图4c所示。由图可知，左右轮在32 kN和46 kN的静轮重下具有基本相同的变化规律。同一静轮重下，左侧车轮磨耗功始终大于右侧，说明磨耗主要发生在左侧轮轨。随静轮重的增大，磨耗功呈上升趋势，在10 s左右时，左右侧车轮磨耗功均达到其峰值，在静轮重46 kN时分别为19 kW左右、6 kW左右。由此可见，磨耗功受静轮重影响较大，即静轮重越大，轮轨间产生的磨耗功越大。

3.4 车辆通过速度控制

本小节计算了埃塞俄比亚有轨电车以速度10 km/h和30 km/h通过半径为50 m的曲线轨道时的各项动力学性能指标，计算结果如图5所示。

不同车速下的轮轨横向力如图5a所示。由图可知，不同车速下的轮轨横向力分布均具有对称性。当车速由10 km/h增大到30 km/h后，右侧轮轨横向力除峰值外略微减小；左侧轮轨横向力增大，且增大幅度较为明显，其车速为10 km/h的轮轨横向力曲线相较于车速为30 km/h的轮轨横向力有较小的滞后效应。在60 m位置附近，左右两侧车轮轮轨横向力均产生峰值，分别为28.00 kN、20.86 kN。

不同车速下的轮轨垂向力如图5b所示。由图可知，各车速下的左右轮轨垂向力具有明显的对称性。其中，左侧车轮处于增载状态，右侧车轮处于减载状态。车速由10 km/h增大到30 km/h后，右侧轮轨垂向力有明显减小，而左侧轮轨垂向力有明显增大。左侧车轮轮轨垂向力始终大于同一速度下的右侧轮轨垂向力，车速为30 km/h时，其峰值在60 m附近产生，约为68.476 kN。车速的改变，导致垂向力的数值有显著变化，可由此指导调整车辆运行的速度。

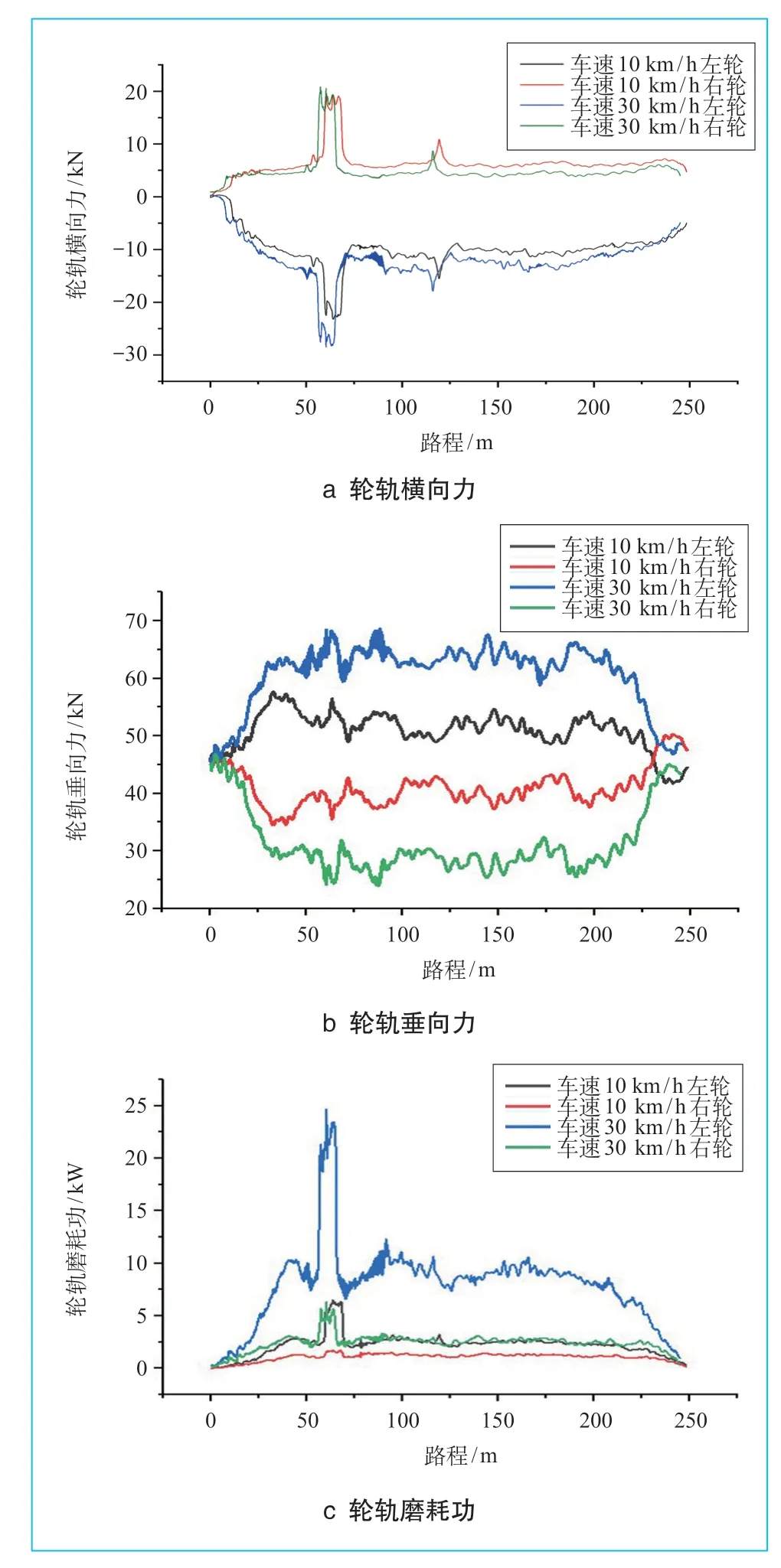
图5 不同车速下动力学指标计算结果

不同车速下的轮轨磨耗功如图5c所示。由图可知，在同一车速下左轮的磨耗功整体上大于右轮，尤其是在峰值位置最为明显。不同速度下两侧车轮磨耗功变化规律基本相同。随着车速的增大，左侧车轮磨耗功的波动幅度增大，磨耗功有明显增大；右侧车轮磨耗功也增大，不过其增大幅度相较左侧车轮而言较小。车速为30 km/h时，左轮磨耗功在60 m附近产生明显峰值，为24.69 kW，远大于车速为10 km/h时的轮轨磨耗功峰值，故对于该侧车轮而言，适当减小车速有利于降低轮轨间的磨耗。

4 结论

针对低地板有轨电车建立嵌入式轨道车线耦合动力学模型，研究和分析不同参数对轮轨动力学和钢轨磨耗变化规律的影响，得到如下结论：

（1）曲线半径是影响小半径曲线轮轨动力学及磨耗程度的关键因素，曲线半径由50 m增大至200 m后，轮轨横向力（左侧车轮）、轮轨垂向力和磨耗功均有较明显的减小；

（2）随着摩擦系数由0.1增大为0.3，横向力减小且脱轨风险降低，但其将导致磨耗的增大；

（3）随着静轮重增大，轮轨磨耗明显增加，横向力和垂向力亦随之增大；

（4）随着车速由10 km/h增大到30 km/h，横向力和垂向力均增大且磨耗功大幅增加。