两种水库库容计算方法的比较分析

李 浩，许 霞，李凌云

（1.山东省水利科学研究院，山东 济南 250014；2.济南市莱芜区水利工程服务中心，山东 济南 250022；3.南京师范大学地理科学学院，江苏 南京 210034）

准确掌握水库库容情况是保证水库正常运行的前提。本文基于日照市青峰岭水库的库底高程实测点数据，应用等高线法和离散点法分别计算水库库容，并与传统人工断面法计算结果进行对比分析，验证这两种方法应用于水库库容计算的可靠性和精确度。

1 两种水库库容计算方法

应用传统人工断面法施测获得的日照市青峰岭水库库底点位三维坐标原始数据，分别采用两种不同方法对各高程下的库容量进行计算，并将计算结果与传统人工断面法计算得到的结果进行比对

1.1 等高线法

该算法以DWG 格式的等高线图为数据依据，等高线图是根据所有测量点的三维坐标成果绘制的。

1）数据预处理。由于等高线图中存在重叠（同一等高线存在两条），因此，在依据等高线生成三角面片时，首先对重叠的等高线进行处理，相同的等高线只能保留一条。处理过程如下：（1）提取所有等高线的数据；（2）计算每条等高线的周长和所围成的面积；（3）比较各等高线的面积和周长，若存在面积和周长相等的等高线，则只保留一条。

2）库底三角网面生成算法。程序框图如图1所示（其中：xmin为等高线的最小 z 坐标，xmax为等高线的最大z 坐标，h 为步长）。

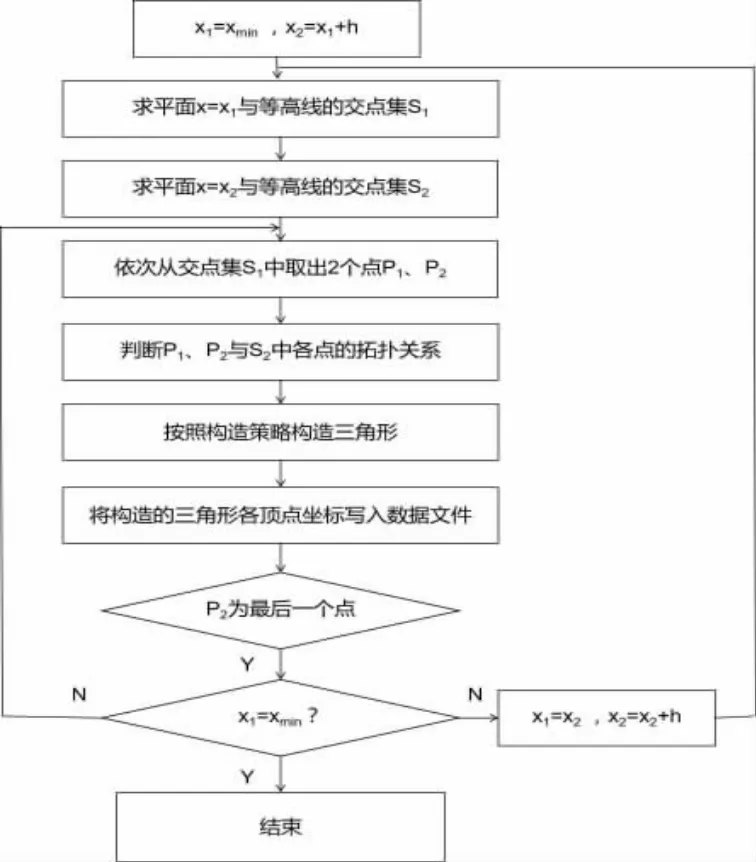
图1 等高线法程序框图

1.2 离散点法

该算法以测量出的库底离散坐标点为计算依据，直接将离散点转换成三角网面。

1）三角网面构造。通过前处理程序测量数据重合点剔除，采用Bowyer-Watson 算法实现库底三角网面的生成。该算法的基本程序是：（1）构造一个初始超级三角形，让这个三角形含括一切散点；（2）将集中的散点按顺序插入，如图 2（a）；（3）在三角形链表中找到其外接圆包含该插入点的三角形，如图 2（b）；（4）然后去除影响三角形的公共边，如图 2（c）；（5）将插入点与影响三角形的顶点全部连接起来，如图2（d）。进而完成一个点在三角形链表中的植入；（6）将新形成的三角形移入进三角形数组；（7）循环执行第2 步操作，直到全部散点植入完成。

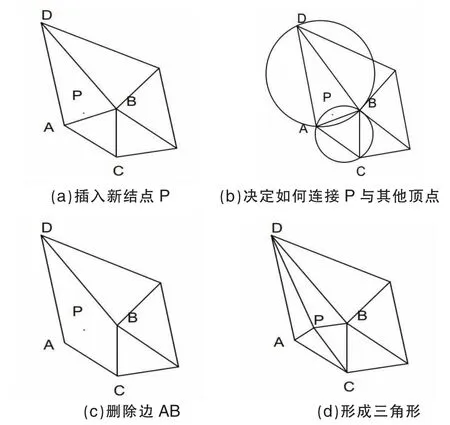
图2 Bowyer-Watson 算法过程

离散点法程序框图见图3。

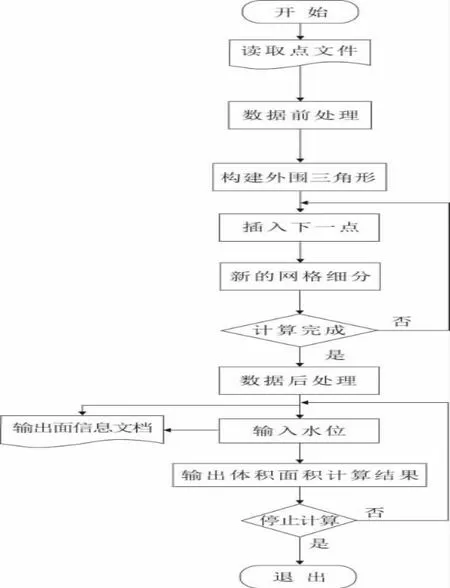
图3 离散点法程序框图

该算法逻辑严密、唯一性好，并且在构建网格的过程中，当需要增加新点时，仅仅对新点的影响三角形范围开展局部联网，不用对所有的点开展重新构网的操作，算法上容易实现并且不易出错。

2）库容计算。库底形状构造完成后，形成含有所有三角形顶点坐标的数据文件，根据该数据文件，可以进行库容量、水面面积、淹没线的计算。

设 Z 为库面高程（库面的 z 坐标），ΔABC 为所构建的库底中的某一三角形，并设A 点高于B点，B 点高于C 点，即：ZA≥ZB≥ZC（ZA表示A 点的Z 坐标，其余相同），则在某一高程值Z 时，ΔABC所对应的库容（体积）及水面面积的计算分下面四种情况（见图4）：

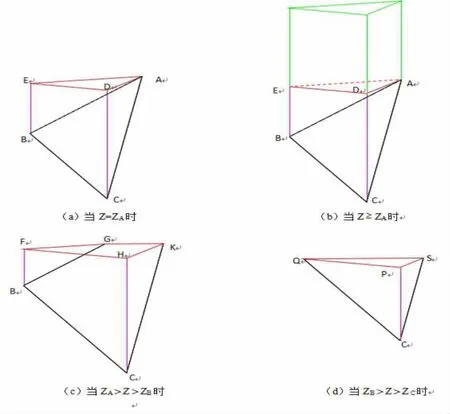
图4 体积计算时的4 种情况

（1）当 Z=ZA时：如图 4（a）所示，E、D 点与 A点等高，且分别与B、C 点具有相同的x、y 坐标，则ΔABC 所对应的库容（体积）为多面体ABCDE的体积，ΔABC 所对应的水面面积为ΔADE 的面积，该三角形不存在对应的淹没线。

（2）当 Z≥ZA时：如图 4（b）所示，ΔABC 所对应的库容（体积）为多面体ABCDE 的体积与以ΔABC 为底面的三棱柱的体积之和，ΔABC 所对应的水面面积为ΔADE 的面积，该三角形不存在对应的淹没线。

（3）当 ZA＞Z＞ZB时：如图 4（c）所示，ZF=ZG=ZH=ZK，点的ΔABC 所对应的库容（体积）为多面体ABFGHK 的体积，ΔABC 所对应的水面面积为四边形FGHK 的面积，直线GK 为该三角形对应的淹没线。

（4）当 ZB＞Z＞ZC时：如图 4（d）所示，ZD=ZQ=ZS=Z，点的ΔABC 所对应的库容（体积）为四面体CPQS 的体积，ΔABC 所对应的水面面积为ΔPQS的面积，直线QS 为该三角形对应的淹没线。

2 计算结果比较分析

两种方法的计算结果如表1 所示。表1 中的误差是指等高线法、离散点法的计算结果相对于传统人工断面法计算数据的偏差。可以看出，两种计算方法得到的结果与传统人工断面法计算结果偏差在可接受范围内，其中离散点法和传统人工断面法计算结果非常接近，等高线法相对于传统人工断面法计算结果的误差略大。这是因为等高线是根据所测得的离散点生成的，在生成等高线的过程中存在着拟合误差。由此可以得出：两种方法应用于水库库容计算是可靠的，且离散点法的计算精度更高。