具有一步随机滞后和丢包多传感器系统分布式递推融合预报器

魏 瑶, 孙书利

(黑龙江大学 电子工程学院，哈尔滨 150080)

0 引 言

21世纪的控制系统结合了网络通信和控制，随着网络技术与控制技术的融合，出现了系统组件间通过网络交换信息的网络化控制系统，并且在计算机通信领域的研究与应用日益广泛。近年，有关网络化系统控制和估计问题的研究引起了人们的广泛关注[1]。

由于不可靠的网络环境，数据在通信通道中传输不可避免出现随机滞后、丢包、观测丢失、多采样速率等现象。传统估计理论和控制理论对于上述不确定性系统不再适用，对此需针对上述问题重新建模，分析规律，设计相应的估计理论和控制理论[2-4]。对已知数据包是否丢失系统，文献[5]提出间断观测卡尔曼滤波器，并给出了保证不稳定系统滤波器稳定的观测接受率的上界和下界。文献[6]对文献[5]进行了推广，当系统的观测性矩阵可逆时，临界接受率的下界就是临界接受率。文献[5]提出的滤波器不具有稳态，需要在线计算。为减小计算负担，文献[7]应用线性矩阵不等式方法设计了一种次优稳态H2滤波器。对不带时间戳系统，文献[8-10]研究了仅含有随机时滞系统的状态估计问题，文献[11]考虑了带随机跳跃时滞的单传感器和多传感器系统的状态估计问题。考虑与文献[7]相同的观测模型，依靠观测数据丢包概率，文献[12]推导出了最优线性估值器，同时给出了稳态滤波存在的一个充分条件。

在网络化系统中，数据传输过程中不可能出现无限丢包现象，文献[13-14]研究了有限持续丢包系统的最优和次优滤波器。文献[15-17]研究了仅含有丢失观测系统的状态估计问题。综合考虑滞后和丢包现象，文献[18]研究了一步滞后和多丢包系统的最优滤波算法，并给出了稳态存在的充分条件。上述文献考虑了随机噪声，但不能处理非随机噪声干扰。考虑到数据重发机制，文献[19]提出了最优线性滤波器。针对带多步滞后和多丢包系统，对有/无时间戳情形，文献[20]分别提出了最优线性滤波器。文献[21]在文献[18]的基础之上，研究了多传感器系统的融合估计问题。对具有不同丢包率的多传感器系统，文献[22]提出了最优集中式和分布式融合估值器。以上文献所提出的有关融合估值器大都是基于局部估计的矩阵加权融合算法[23]。但没有考虑多传感器融合中的先验融合估计。文献[24-25]考虑了先验融合估计，提出了一种分布式递推融合算法，但是没有考虑数据传输中可能出现的随机滞后和丢包问题。

针对具有一步随机滞后和多丢包多传感器系统，应用文献[25]中的分布式递推融合估计算法，在线性无偏最小方差准则下，提出了具有Kalman递推结构的分布式递推最优线性融合预报算法，分析了算法的稳定性和稳态特性。

1 问题阐述

考虑如下离散时间线性随机系统[26]:

x(t+1)=Fx(t)+Dω(t)

(1)

y(p)(t)=C(p)x(t)+v(p)(t)

(2)

其中:x(t)∈Rn为系统状态，y(p)(t)∈Rmp，p=1,2,…,N为传感器观测。ω(t)∈Rr和v(p)(t)∈Rmp分别为过程噪声和观测噪声，N是传感器的个数。F，D和C(p)为合适维数的常矩阵。

假设1：ω(t)和v(p)(t)为带有零均值的相关白噪声

(3)

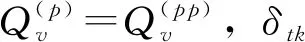
假设2：初始状态x(0)的均值为μ0，方差为P0，且与噪声ω(t)和v(p)(t)不相关。

假设3：F为稳定矩阵。

数据通过网络从传感器传输到数据处理中心时，存在一步滞后和多丢包现象，传感器一个数据包只传输一次，估值器每一时刻只收一个数据包，若某一时刻没有接收相应时刻的数据包，就用前一时刻接收的数据来代替，因此，估值器所接收到的测量值可通过如下模型描述：

(4)

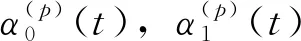
本文研究的问题是基于收到的多传感器观测数据(y(1)(t),…,y(1)(0),…,y(N)(t),…,y(N)(0))，设计分布式递推融合预报器。首先，根据各传感器的观测数据设计局部预报器，然后得到局部传感器间的互协方差。最后设计出分布式递推融合预报器，并与集中式和矩阵加权分布式融合进行比较。

2 局部最优线性滤波器

2.1 模型转化

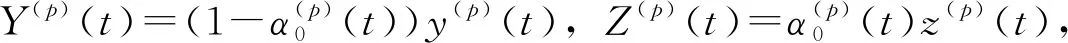
(5)

(6)

系统(1)～(2)可转化为随机参数系统：

(7)

(8)

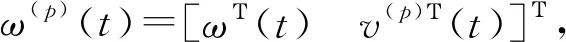
(9)

式(9)满足

(10)

(11)

(12)

其中:

(13)

对于系统(7)～(8)，可获得统计信息：

(14)

系统进一步可以被转化为常系数矩阵形式：

(15)

(16)

其中，虚拟过程噪声W(p)(t)和虚拟观测噪声V(p)(t)为

(17)

(18)

2.2 预备引理

(19)

定义：

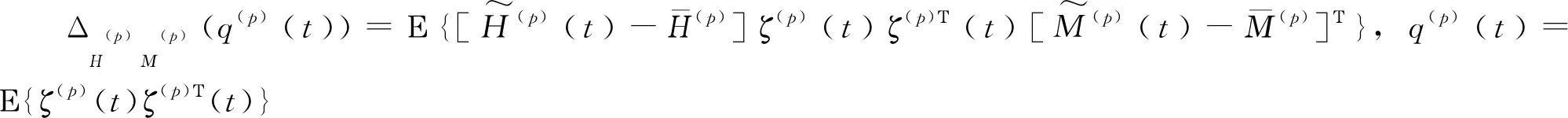
引理2：对系统(15)～(16)，在假设1和假设2下，统计信息成立：

(20)

(21)

(22)

(23)

(24)

(25)

引理3：对于系统(15)～(16)，在假设1和假设2下，状态的二阶矩阵满足推导公式

(26)

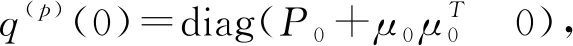
2.3 局部线性预报器

引理4：对于系统(15)～(16)，局部传感器子系统的线性最优局部预报器为

(27)

(28)

(29)

(30)

(31)

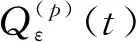
2.4 互协方差阵计算

引理5：对于系统(15)～(16)，在第p和第q传感器子系统之间的预报误差互协方差阵分别为

(32)

其中：P(pq)(t+1|t)为一步预报误差互协方差阵。

传感器新息ε(p)(t)和ε(q)(t)之间的互协方差阵为

(33)

其中:初值为P(pq)(0|-1)=diag(P0,0)。

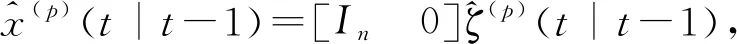
3 分布式递推融合预报器设计

定理1：系统(15)～(16)在假设1和假设2下，基于局部一步预报估值，可得具有Kalman递推形式的分布式线性无偏最小方差最优融合预报器：

(34)

预报器增益矩阵L(t)计算为

(35)

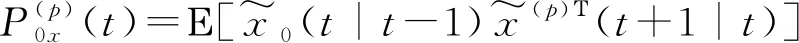
(36)

(37)

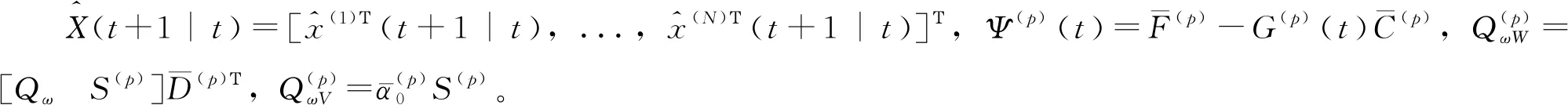
(38)

矩阵Λ(t)计算：

(39)

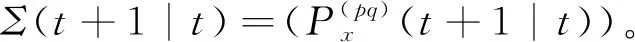
融合预报误差方差阵P0(t+1|t)递推计算：

(40)

初值为P0(0|-1)=P0。

证明：式(1)减去式(34)，得到分布式递推融合预报误差为

(41)

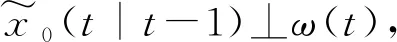
(In-L(t)J)[FP0(t|t-1)FT+DQωDT](In-L(t)J)T+L(t)∑(t+1|t)LT(t)+

(42)

由式(15)，式(27)和式(28)，得到增广状态局部传感器pth预报误差为

(43)

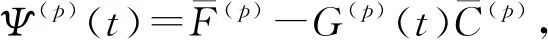
(44)

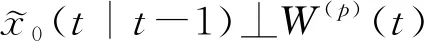
(45)

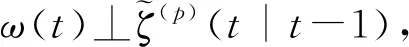
将式(42)重写成：

P0(t+1|t)=FP0(t|t-1)FΤ+DQωDΤ+{L(t)-[FP0(t|t-1)FΤJΤ+DQωDΤJΤ-

(46)

其中，Λ(t)满足式(39)，为了使预报误差方差最小，上式等号右侧第3项为零，可得分布式递推融合预报增益式(35)，分布式递推融合预报误差方差为式(40)。

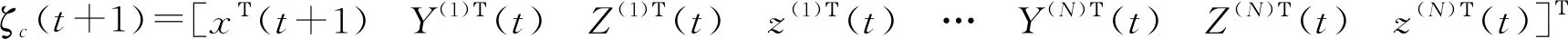
4 稳定性和稳态分析

引理6：由假设3可知，状态二阶矩q(p)(t)在任意初值q(p)(0)≥0条件下收敛于如下Lyapunov方程的唯一的半正定解q(p):

(47)

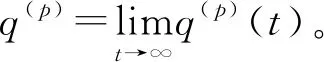
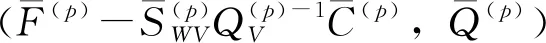
(48)

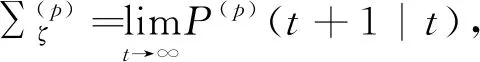
稳态预报器

(49)

是渐近稳定的。

(50)

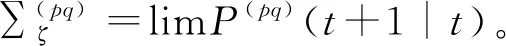
由式(42)，分布式递推融合预报误差方差为

P0(t+1|t)=(In-L(t)J)FP0(t|t-1)FΤ(In-L(t)J)Τ+(In-L(t)J)DQωDΤ(In-L(t)J)Τ+

(51)

定理2：在假设3下，带有任意初值的融合预报误差方差式(51)的解收敛于Riccati方程的唯一半正定解：

(52)

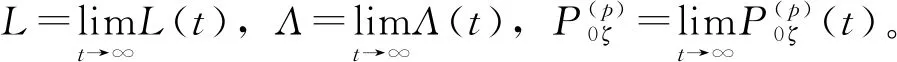
而且，分布式稳态融合预报器

(53)

是渐进稳定的。

证明：由式(43)，得

(54)

其中，W(t)=[W(1)Τ(t),…,W(N)Τ(t)]Τ，V(t)=[V(1)Τ(t),…,V(N)Τ(t)]Τ，G(t)=diag(G(1)(t),…,G(N)(t))，Ψ(t)=diag(Ψ(1)(t),…,Ψ(N)(t))。

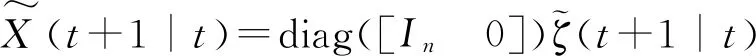
(55)

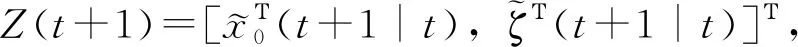
(56)

协方差阵为PZ(t+1)=Ε[Z(t+1)ZΤ(t+1)]为

PZ(t+1)=

(57)

(58)

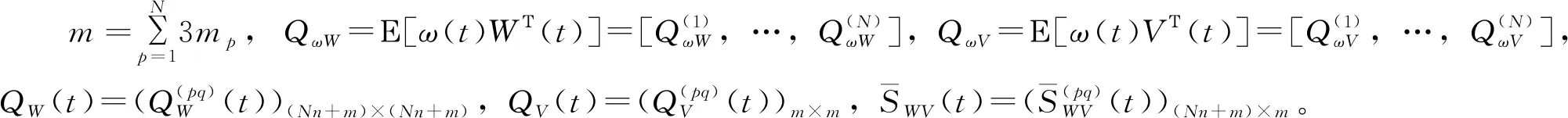
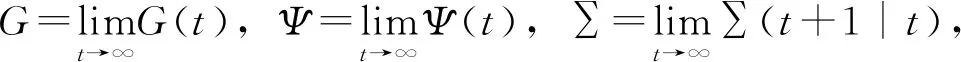
5 仿真例子

考虑带一步滞后和多丢包不间断电力系统(UPS)

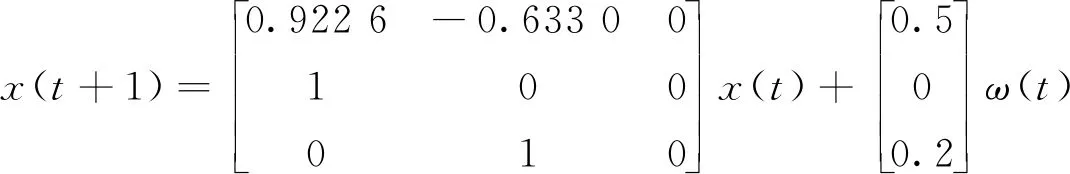
(59)

z(p)(t)=H(p)x(t)+v(p)(t)，p=1,2,3

(60)

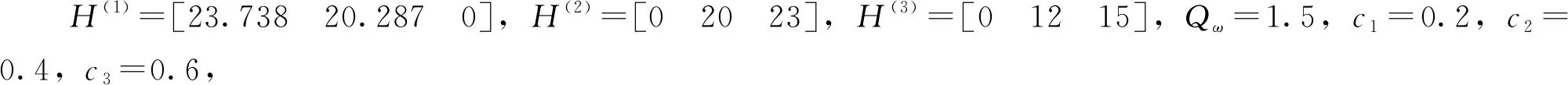
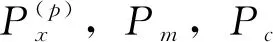
图1 分布式递推融合预报器

表1 第一个状态分量的稳态预报误差方差比较

表2 第二个状态分量的稳态预报误差方差比较

表3 第三个状态分量的稳态预报误差方差比较

6 结 论

本文对具有一步滞后和多丢包的多传感器系统，设计了基于线性无偏最小方差准则的分布式最优融合预报算法，该算法基于先验融合预报器和局部预报器计算，具有递推结构。首先引入新变量，将原系统转化为具有随机参数的等价系统，应用新息分析方法，设计了线性最小方差最优局部预报器。然后推导了局部预报误差互协方差阵、以及先验融合预报与局部预报误差互协方差阵。在此基础之上，得到了分布式递推融合预报器。给出了稳态预报器存在的一个充分条件，分析了分布式递推融合预报器的稳定性。与矩阵加权融合预报相比具有更好的估计精度。