静电雾化喷头喷针布局方式的分析与优化

刘建河，石亮,闫晨阳，吴秋月

(长春理工大学机电工程学院，吉林 长春130022)

静电喷雾是近年来发展起来的一项新技术.通过静电喷雾机使农药雾化并使雾滴带电，可以使雾滴的命中率提高、分布均匀(尤其是使植物叶片的背面能附着雾滴)，黏附牢固，飘失减少，从而提高农药的利用效率，降低农药的用量，减少农药对环境所造成的污染[1].该工艺由于其独特的优点，在表面涂层、乳液或超微细气雾剂生产、燃料喷雾、微封装、喷墨打印机和胶体微推进器等领域都有着广泛的应用[2-4]，近些年更是有学者将其应用到雾化吸入等医疗领域.

由于单毛细管电雾化时存在流量太小的问题，研究人员近年来开始了多毛细管静电雾化的研究，刘明明等[5]通过采用传统的金属毛细管搭建了多喷管电雾化试验装置，初步获得了多管道电雾化喷洒的各种模式，并比较了乙醇在单、多管道条件下“锥-射流”模式喷洒的两个重要指标:稳定喷洒的起始电压和电流-流量关系.高全杰等[6]建立了多针电极喷雾刀梁静电场的数学模型，运用Ansoft Maxwell软件分析了多针电极喷雾刀梁空间中电压及电场强度，并探讨了针电极间距对静电场的影响.MOON等[7]研究了通过优化多孔喷油器的孔排列方式来改进柴油混合物的制备.以上都为多针静电喷头的设计研究提供了指引作用.

在此前学者的研究基础上，文中建立多针喷嘴为平板电极静电场求解模型，利用Ansoft Maxwell软件，获得各种静电喷头周围平面电场强度分布特征以及特殊路径下电场分布曲线，并进行雾化液滴粒径测量试验，为开发新型静电喷头提供理论依据及试验基础.

1 建模与仿真

1.1 物理模型

目前比较成熟的荷电方式主要有接触荷电、感应荷电、电晕荷电3种[8].静电喷雾的通用物理模型如图1所示，其中N为由毛细金属管制成的喷嘴，液流j以速度v从喷嘴流出.C为环形电极，P为尖端电极，L1，L2，L3为连接导线.按不同的电位组合，当L1，L2接地，L3接电压源时，金属尖端P会使周围空气击穿，此为电离电场充电；如果把导体L1连接到电压源，L2，L3接地，则为接触充电；如果导体L1和L2之间接电压源，在圆筒形电极C上加一正电位，射流保持对地电位，则形成感应充电.

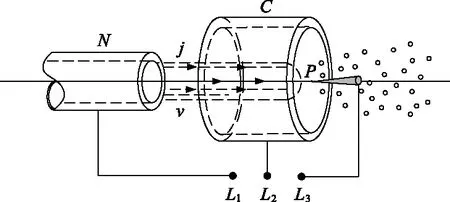
图1 静电雾化的物理模型

在3种充电方式中，相比较于感应充电与电晕充电，接触充电由于高压电极直接连接到金属喷头或液体上，使雾滴带上同高压电极极性相同的电荷，雾滴荷电最为充分，充电效果最佳[9-10]，因此文中充电方式选用接触充电.

1.2 静电场数学求解模型

充电电场是决定静电雾化的关键因素，静电喷雾的首要条件为在对电极间形成高压静电场，继而发生破碎达到雾化的目的，因此电场强度及其分布特性直接决定着液体的静电雾化效果.以下将首先讨论喷嘴周围的电场分布特性.

求解电场分布就是在一定条件下求解麦克斯韦方程等势函数.电场中的势方程满足拉普拉斯方程或泊松方程.真空中的麦克斯韦方程为

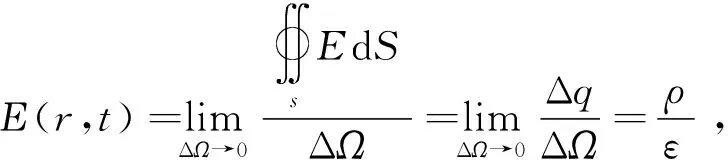
(1)

式中：E为电场强度，N/C ；S为电荷流截面积，m2；q为电荷量，C；Ω为场域，m2；ρ为电荷密度，C/m2；ε为气相介电常数，F/m.

由于喷嘴周围的介质为均匀介质空气，因此均匀线性介质的介电性能方程为

D=εE,

(2)

式中:D为电位移矢量.

喷雾针周围空气介质的麦克斯韦方程为

∇D(r,t)=ρ(r,t),

(3)

根据电势，空间电场强度为

E=-∇φ,

(4)

式中:φ为空间电势.

求解喷嘴周围静电场分布的问题可以转化为用泊松方程和拉普拉斯方程求解标量得到空间电势分布，再用式(4)得到电场强度的问题.

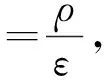
(5)

忽略喷嘴附近电荷的影响，空间电势可用拉普拉斯方程来描述.当电场中没有电荷分布，即ρ=0时，得

∇2φ=0,

(6)

式中:∇2为拉普拉斯算子，在直角坐标系中展开为

(7)

静电场分布问题，可简化为从求场强(矢量)变成求电势(标量)的问题.电势φ可以根据电荷分布和边界条件来计算.

1.3 有限元法求解模型

有限元法是1种基于变分原理和近似插值离散化的数值方法.在求解静电场问题的泊松方程(5)时，当在场域为Ω时，它的等价函数为

(8)

此函数取得极值的函数必须满足式(5)，因此将式(5)的求解问题转化为式(7)的函数极值问题.将式(7)中场域的积分转化为各单元上的积分之和，再将势函数近似表示得到各单元上的积分，从而将式(7)转化为非积分的多元函数.

=φTSφ-φTG，

(9)

式中：S,G为已知系数矩阵.

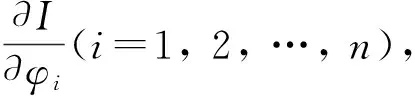
1.4 有限元计算

倾向于将喷针均匀排列使得相互之间的影响是同等的，因此选用3种常见阵列方式：正方形阵列、圆周阵列以及正六边形阵列，圆周阵列半径为8 mm，正方形与正六边形外接圆半径为8 mm，3种阵列方式喷针数量皆为12根且等距排列.对此3种阵列方式形成的电场分布进行仿真分析.

通过前期试验中调整电压流量值大小，根据雾化液滴粒径分布情况，初步确定了喷头的相关尺寸，相关参数设置如下：喷嘴材料设为黄铜，喷嘴外径为22 mm，壁厚为1.5 mm，喷针长度为10 mm，内径为0.14 mm，外径为0.20 mm，平板电极的材料设为Al-N，长为220 mm，宽为120 mm，厚为2 mm.文中仿真采用自适应划分，设置每步增加的单元为15%，自适应的总步数为30，误差为0.01%.最后，选取空间内最能反映其空间电场分布的重要平面，获得相应的电场分布云图，并在该平面内选取特殊路径，得到路径上电场强度的数值变化曲线.

1.4.1 不同阵列方式对电场强度的影响

电场强度分布云图能够清晰地显示平面内各位置的电场强度强弱分布，各模型在竖直方向上的总体结构相似，因此选择YOZ平面(喷嘴中心剖面)，且任选1种模型(正方形阵列)，观察了电场在该平面上的大致分布情况，如图2所示，同时选择喷针顶端所在平面，获得3种模型喷针末端所在平面电场分布云图如图2b，c，d所示.

图2 不同阵列方式电场分布云图

图2a反映了各种模型电场在竖直面上的大致分布情况，电场强度呈对称分布，喷嘴各边界端点处电场强度最高，而根据平面分布，图2b-d中，3种阵列方式的喷嘴为平板电极形成的电场分布趋势近乎相同，距离中心越远，场强分布越发散.

为了从数值上观察电场的变化规律，在Maxwell的后处理中，在竖直方向上创建1条由点(0,0,2)到(0,0,102)的特殊线段，经分析得到该路径竖直方向上的电场强度值变化趋势如图3所示，图中纵坐标表示电场强度值E，横坐标表示与起始坐标的距离d.

图3中，在给定路径上，自最远端(0,0,2)到距离喷针最近处，电场强度逐渐增大，在距喷针端点最近处出现电场强度极大值，后又逐渐减小，直至喷针与底座接触处，在该位置电场强度骤降为0，在壁厚2 mm的底座底面内部场强持续为0，之后逐渐升高，在底座开口平面处出现新的极值点,在此之后电场强度又逐渐减小.

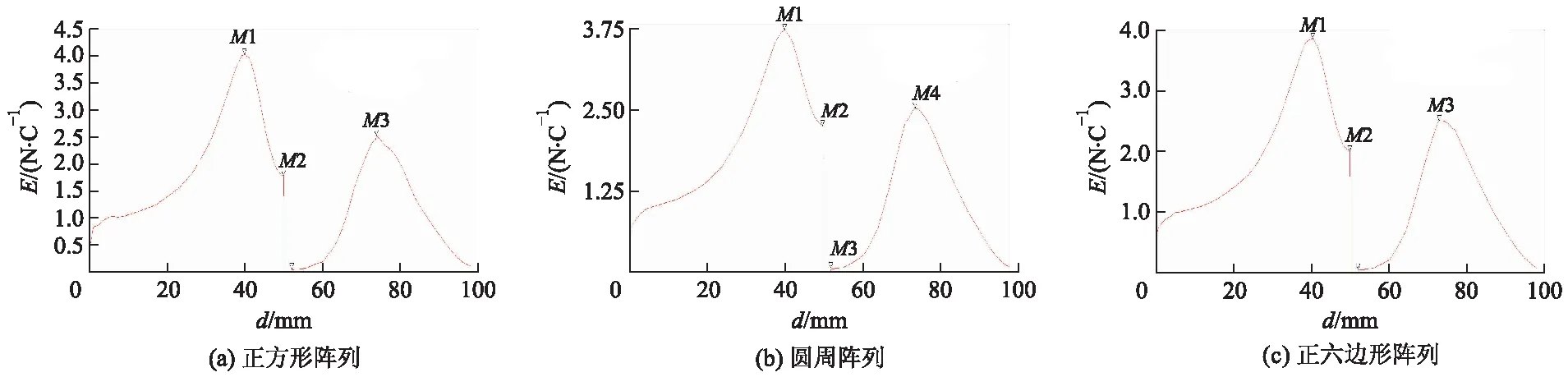
图3 不同阵列方式竖直方向上电场强度值变化曲线

为了更加精确地表达不同阵列方式的影响程度，通过特殊点的具体数值来显示三者的区别，选定以(0,0,52)为节点的前后两段区间内的2个极大值点(M1,M3)与2个折点(M2,M4)，具体电场强度数值如表1所示.

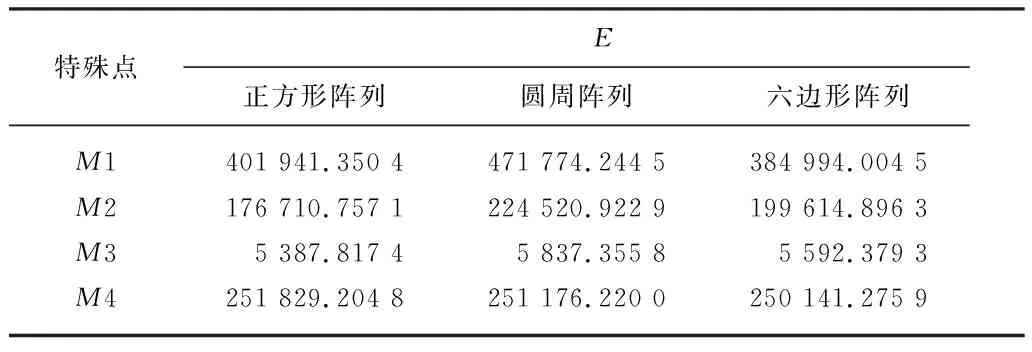
表1 不同阵列方式下各特殊点处电场强度值

3种阵列方式在各极大值处的电场强度各不相同，从表1中数值可以直观看出，圆周阵列相比较于其他2种阵列方式，在同样位置处几乎所有电场强度值都更大，其形成的电场强度分布优于其他2种方式，这有利于提高静电雾化液滴的均匀性以及荷电能力，从而改善雾化效果.因此优选圆周阵列作为雾化喷头喷针的阵列方式，在此基础上，设计3种不同半径分布的情况，对这一因素作进一步讨论.

1.4.2 不同分布半径对电场强度的影响

依照上述仿真流程，将其他参数固定不变，选取3个不同的分布半径R(6，7和8 mm)，3种情况下喷针末端所在平面的电场强度分布云图如图4所示.

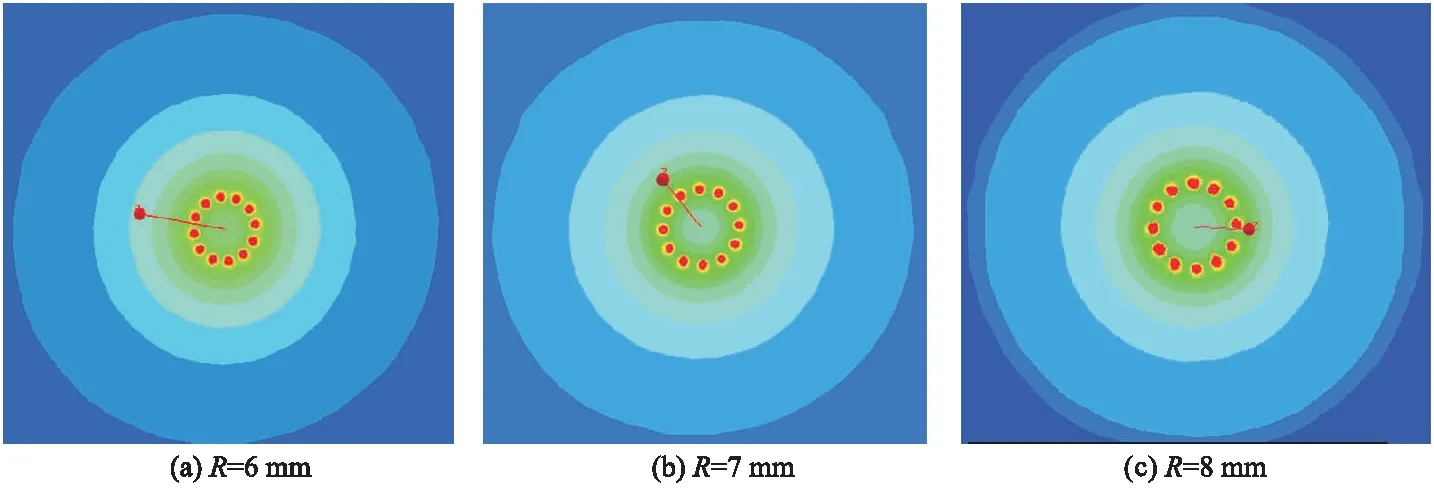
图4 不同分布半径的电场分布云图

同样，为了从数值上观察电场的变化规律，竖直方向上绘制一条由点(0,0,2)到(0,0,102)的一条线段，分析后得到该路径上的电场强度变化趋势.

3种半径分布的电场强度分布云图与数值变化曲线变化趋势与前述相似，在此不再赘述.同样通过特殊点的具体数值来显示三者的区别，选定以(0,0,52)为节点的前后两段区间内的2个极大值点(M1,M3)与2个折点(M2,M4)，具体电场强度数值如表2所示.

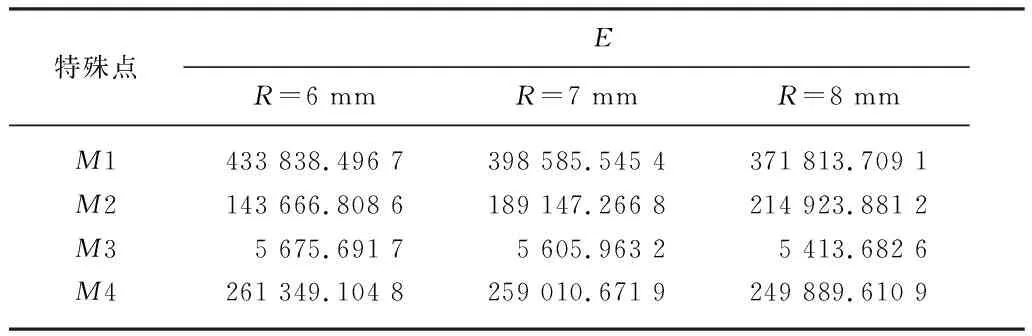
表2 不同分布半径各特殊点处电场强度值

3种不同半径在各极大值处的电场强度各不相同，从表2中数值可以直观看出，除了点M2处，半径为6 mm时，各电场强度值均为最高，因此，总体上，此时形成的电场强度分布优于其他2种情况，可见，减小喷针圆周阵列的半径，能够得到更高的平均电场强度.

2 对比试验研究

2.1 试验装置

为了对以上仿真结果进行有效验证，设计2组对比试验.搭建如图5所示试验平台，由供液系统、静电发生系统、粒子动态分析系统3部分构成.

图5 试验平台

供液系统由注射泵、20 mL注射器和输液管组成.将具有一定电导率(≥10-6S/m，电导率太低时，没有足够的电流流动，导致液体无法喷射雾化.而过高的电导率会导致不稳定的喷雾过程，形成多分散性)的溶液注入毛细管喷嘴后，在毛细管和平板电极之间施加电压，逐渐升高电压进行雾化[11-12].粒子动态分析系统，采用的是欧美克(OMEC)DP-02激光粒度分析仪，可实时测量出雾滴粒径大小和分布.

相关参数设置如下：溶液选用1.8%阿维菌素乳油4 000～4 500倍液[13]，注射泵流量为100 μL/min，电压设置为-10 kV，粒度分析仪中，样品折射率为M-Diff，分散介质为空气，分析模式为polydis，粒径截断下限和上限分别为1 μm与500 μm.

2.2 试验结果

以圆周阵列喷嘴为例雾化后液滴粒径分布结果如图6所示，图中D为液滴直径，α微为液滴粒径微分分布百分比，右侧纵坐标旁α累表示粒径的累积分布百分比.

图6 圆周阵列喷嘴雾化液滴平均粒径值及分布情况

单次试验存在一定的偶然性以及不稳定性，为了减小因此带来的影响，分别对各种喷嘴进行多次测量，试验结果如图7所示.

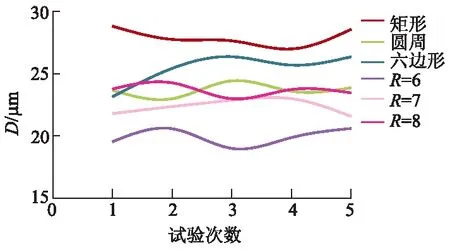
图7 5次试验下不同喷嘴平均雾化粒径分布规律

图6测试报告及图7的多次试验结果曲线图表明，各喷嘴雾化液滴粒径分布均在15～30 μm，而研究表明，农药喷洒雾滴粒径的合理范围为10～50 μm[14]，因此该雾化喷头基本符合设计要求.相同条件下，3种阵列方式获得的粒径分布都呈现较好的单分散性，而采用圆周阵列产生的液滴平均粒径值更小，而圆周阵列方式中，选用更小的喷针分布半径(R=6 mm)时获得的液滴粒径平均值更小，这与此前仿真结果几乎一致.

在后续的补充试验中，对喷针采用更小分布半径阵列的喷头进行了雾化液滴粒径测量试验，发现所得试验数据误差较大，这可能是由于过于紧密的排布产生的过小针距容易击穿空气，从而影响了雾化过程，因此，采用半径为6 mm最为合适.

3 结 论

1) 在相同条件下，3种阵列方式静电场分布趋势相同，数值上看，圆周阵列方式相比较于正方形阵列与六边形阵列，其平均电场强度值更高，这可能是由于其分布对称性更高，而试验结果也验证了这一点，其雾化后的液滴平均粒径值更小.

2) 在采用圆周阵列方式时，同种条件下，喷针采用更小的分布半径(R=6 mm)获得的电场强度值更高，雾化的液滴平均粒径值更小.

3) 过于紧密的排布产生的过小针距容易击穿空气，从而影响雾化过程，因此，采用半径为6 mm的排布方式最为合适.