基于全因子试验碱液循环泵固液两相流数值计算与性能预测

李伟，王磊，施卫东，常浩，吴普，曹卫东,4

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013； 2. 江苏大学镇江流体工程装备技术研究院，江苏 镇江 212009； 3. 南通大学机械工程学院，江苏 南通 226019; 4. 济宁安泰矿山设备制造有限公司， 山东 济宁 272300)

碱液循环泵在实际运行中，单相运行泵的效率较高，但输送介质通常含有固相颗粒如碳酸钙、熔融烧碱等，过流部件被磨损程度受固相属性影响较大[1-2]，且泵性能较清水单相运行时存在不同程度的下降[3].目前国内外关于泵送固液两相介质的研究主要集中在固相的运动规律及其与流场之间的单向耦合作用造成的磨损以及固相组分对泵性能影响等方面，研究手段主要为数值计算与试验测量等.MEHTA等[4]应用PIV技术测量了不同转速下渣浆泵输送不同固相质量浓度的颗粒运动情况，发现叶轮转速与固相速度呈正相关.SALIM等[5]通过试验研究了转速、固相质量浓度和粒径对泵性能的影响，发现固相质量浓度和粒径对泵性能影响较大.CHEN等[6]采用数值计算与试验相结合的方法对熔盐泵流场进行研究，发现颗粒粒径、泵进口颗粒体积分数、叶片数对泵性能有显著影响，且当颗粒粒径过小时泵性能甚至高于单相流泵.GU等[7]研究了不同固相质量浓度对非光滑离心泵叶轮的影响，发现固相质量浓度越大，泵扬程越高，而效率越低.NOON等[8]通过对输送高温石灰浆的离心泵进行数值计算，发现温度对泵性能和磨损侵蚀速率影响较大.FARD等[9]发现改变叶轮结构参数可改善由于泵送黏度较高介质造成的性能下降.

近年来，固液两相流计算模型得到了快速发展，其中欧拉-欧拉法将固液两相视为连续介质和准连续介质，在固液两相流离心泵中得到广泛应用[10-11]，主要适用于高质量浓度计算；欧拉-拉格朗日法[12]将固体视为离散相，采用拉格朗日法求解，而流体采用欧拉法求解，由于需要追踪每个颗粒的运动轨迹，主要用于低质量浓度求解.随着数值计算技术的发展，欧拉-拉格朗日法正成为固液两相流求解的主要手段.施卫东等[13]通过欧拉多相流模型对比分析了不同粒径和不同质量浓度下固相对过流部件的冲刷磨损情况.WEN等[14]采用CFX中Euler-Lagrange耦合模型与Finnie磨损模型探究了深海采矿泵磨损特性.ZHAO等[15]采用双欧拉多相流模型结合均匀平衡模型对三维瞬态过程进行了数值模拟，表明泵的湍动能分布及脉动值均与固相质量浓度正相关.

鉴于碱液循环泵的输送介质含固相的相关属性不断变化，无法针对碱液循环泵输送含有特定体积分数、密度、粒径的固相介质进行有效地性能预测，文中结合统计学方法定量分析输送两相介质的泵内部属性，进而预估其性能.

1 数值计算

1.1 计算模型及边界条件设置

选取HTJ100-80型碱液循环泵为研究对象，该泵设计性能参数分别为流量Qd=100 m3/h，扬程H=32 m，效率η=77%，转速n=2 950 r/min.考虑到碱性工作条件并兼顾输送固液两相介质，叶片厚度较大且耐腐蚀及磨损.

应用计算流体动力学软件ANSYS CFX 17.1对碱液循环泵进行全流场数值计算，计算域包括进水管、前腔、叶轮、蜗壳和后腔，如图1所示.单相介质设为水，采用压力进口边界条件，设为1.013×105Pa，出口边界条件采用质量流量出口，设为27.77 kg/s.基于结构化网格，采用Standardk-ε模型.考虑到碱液循环泵输送溶液中混有碳酸钙(CaCO3)，选用CaCO3颗粒作为第二相.采用双欧拉模型，由于固相体积分数变化较大，低体积分数时选用曳力模型为“Schiller Naumann”.

图1 计算模型

1.2 数值计算的可靠性验证

在江苏大学国家水泵及系统工程技术研究中心水泵实验台进行试验.试验开始前，关闭阀门，待泵在额定转速下运行稳定后，根据所需试验工况点，缓慢调节阀门至相应开度，再待泵运行稳定后，获得HTJ100-80型碱液循环泵在不同流量工况下的扬程、效率等数据，并与数值计算结果进行对比，如图2所示.

图2 碱液循环泵数值计算及试验性能曲线

由图2可以看出：在设计工况1.0Qd时，计算扬程与试验扬程的误差为4.69%，计算效率与试验效率误差为1.07%；在0.2Qd～1.4Qd工况，在设计流量点附近计算和试验的扬程、效率误差较小，而最大误差均出现在1.4Qd，这可能是由于对计算模型进行了简化，部分水力损失未考虑在内，使得偏工况运行时计算结果出现了一定偏差；整体上，计算结果较为准确地反映了碱液循环泵的单相流动规律，表明该数值计算方法是可靠的.

2 基于因子试验的外特性相关度分析

目前的碱液循环泵多是基于清水设计方法，而当碱液循环泵输送溶液中含有CaCO3颗粒时，颗粒属性对碱液循环泵的外特性有较大影响.文中对输送含有CaCO3颗粒的碱液循环泵外特性进行定量预测及颗粒运动特性进行研究.

2.1 全因子试验设计

基于本课题组前期对固液两相流泵的研究成果，对碱液循环泵输送固相颗粒的直径(d)、体积分数(φ)、密度(ρ)等物理属性进行三水平取值分析，如表1所示，并选取泵的扬程和效率作为响应值.为了充分考虑固相颗粒属性主效应及固相颗粒不同属性间的交互作用，采用全因子试验设计，在设计工况1.0Qd时进行了27次试验.

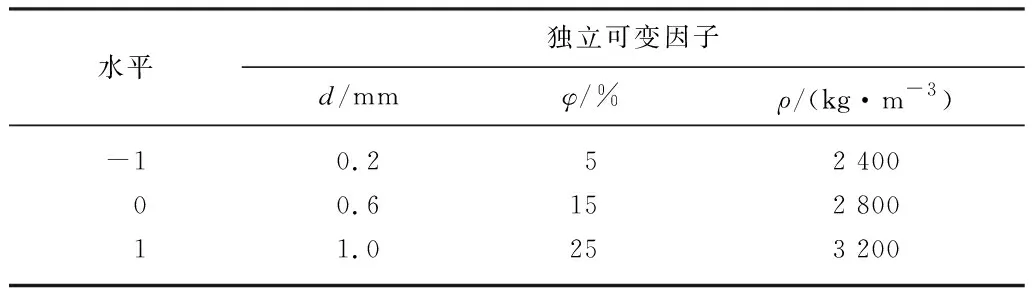
表1 因子设置

2.2 试验因子的影响

在颗粒直径、体积分数、密度不同组合下，碱液循环泵的外特性较清水性能差异较大.采用Minitab软件对试验数据进行处理，评估所有因子的主效应和各阶交互作用.

图3为颗粒参数对碱液循环泵的扬程及效率显著性的Pareto图.由图3a可以看出，颗粒体积分数(φ)、颗粒直径(d)、颗粒密度(ρ)、颗粒直径×颗粒体积分数(dφ)、颗粒体积分数×颗粒密度(φρ)对扬程有显著影响，而颗粒直径×颗粒密度(dρ)对扬程的影响较小，在改进模型拟合扬程的回归方程中可以去除；由图3b可以看出，颗粒体积分数(φ)、颗粒密度(ρ)、颗粒体积分数×颗粒密度(φρ)、颗粒直径(d)对效率有显著影响，而颗粒直径×颗粒体积分数(dφ)和颗粒直径×颗粒密度(dρ)对效率的影响较小，在改进模型拟合效率的回归方程可以去除.

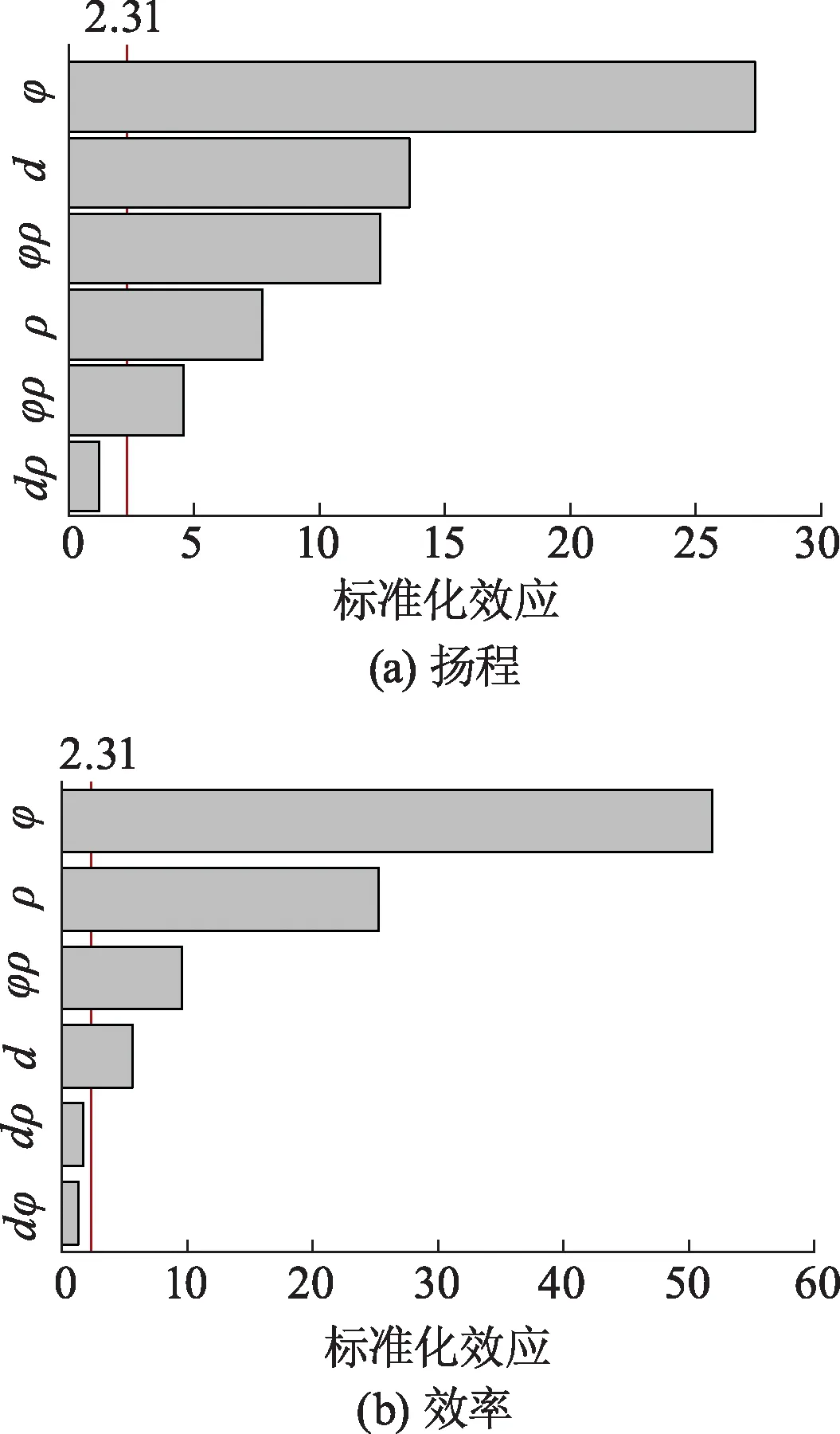
图3 颗粒参数对泵扬程及效率显著性的Pareto图

综合考虑颗粒体积分数(φ)、颗粒密度(ρ)、颗粒直径(d)对设计流量工况下扬程和效率的作用机理可以发现，试验设计要求扬程、效率都不可以太小.根据影响碱液循环泵扬程和效率主效应，颗粒体积分数(φ)和颗粒密度(ρ)影响较为显著，而颗粒直径(d)显著性较弱；根据二阶交互效应，颗粒密度×颗粒体积分数(φρ)较显著，其他交互作用对设计工况下的扬程、效率显著性较差.

图4为颗粒参数对扬程和效率的主效应，由图4a可以看出：从低水平到高水平，颗粒体积分数和颗粒密度的回归线斜率均较大，即两者对设计工况点的扬程影响较大；从低水平增加至高水平，颗粒直径的回归线斜率逐渐减小，趋于平坦，故影响逐渐减小.由图4b可以看出：随着颗粒体积分数和颗粒密度由低水平到高水平，设计工况下的效率不断减小；颗粒直径由小至大，对效率的影响较小，在Pareto图中，颗粒直径对效率显著，说明其对效率也有一定的影响.

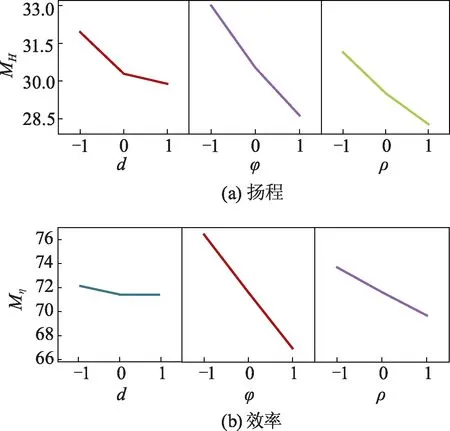
图4 颗粒参数对泵扬程和效率的主效应

颗粒参数对泵扬程和效率的交互作用如图5所示,可以看出：dρ(颗粒直径×颗粒密度)的交互线几乎平行，说明dρ对设计工况下扬程没有显著影响；dφ(颗粒直径×颗粒体积分数)与φρ(颗粒体积分数×颗粒密度)的交互线均不平行，且交叉趋势明显，表明两者之间的交互作用明显；dφ(颗粒直径×颗粒体积分数)的交互线和dρ(颗粒直径×颗粒密度)的交互线几乎平行，说明对设计工况下效率没有显著影响；φρ(颗粒体积分数×颗粒密度)的交互线不平行，表明对于效率而言，两者交互作用明显.

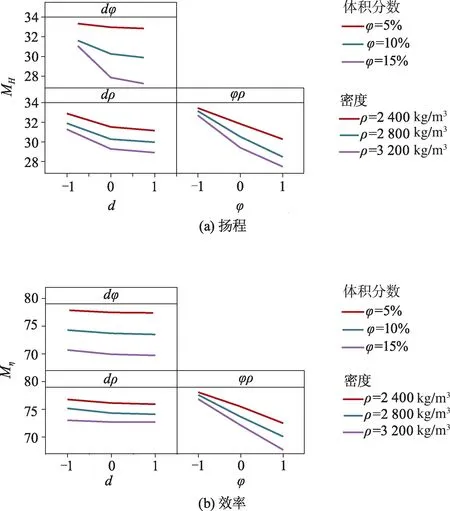
图5 颗粒参数对泵扬程和效率的交互作用

3 流场分析

碱液循环泵输送溶液中混有CaCO3颗粒，颗粒直径、密度和体积分数对碱液循环泵中颗粒的分布和运动轨迹均有显著影响，导致泵内出现复杂内部流动以及出现不同程度的磨损.

在设计工况1.0Qd下，颗粒体积分数为15%，密度为2 800 kg/m3时，计算得到不同颗粒直径下叶轮中间截面的固相体积分数分布，如图6所示.

图6 不同颗粒直径下叶轮中间截面固相体积分数分布

由图6可以看出：相同密度、体积分数但直径不同的颗粒在碱液循环泵内的分布具有一定的规律性，颗粒均沿着压力面流入蜗壳，在蜗壳外周壁面内的流动轨迹具有条纹状特点；随着颗粒直径的增大，导致颗粒质量变大，固相与液相分离加剧，颗粒的运动轨迹越不容易被液相改变，沿着工作面甩出的尾迹越大，颗粒在叶轮流道中的分布区域不断减小，越来越集中于压力面，从而加剧压力面的磨损；进入蜗壳后，由于失去叶轮的离心力作用，固相液相的动能一部分转化为压力能，直径较大的颗粒受到液相的裹挟作用变弱，速度下降较快，愈加向隔舌和蜗壳外周壁面聚集，磨损加剧，受到壁面碰撞后向两边扩散.

在设计工况1.0Qd下，颗粒直径为0.6 mm，体积分数为15%时，计算得到不同颗粒密度下叶轮中间截面的固相体积分数分布，如图7所示.可以看出，随着颗粒密度的增大，受到同等的离心力作用下，固相受到液相的裹挟作用变弱，颗粒在叶轮工作面短暂堆积后向蜗壳流道转移，使得颗粒在叶轮流道的条状分布变窄，蜗壳流道内固相液相之间的分离愈加明显，外周壁面高体积分数颗粒分布区域变大，隔舌处颗粒聚集明显，造成壁面局部磨损.

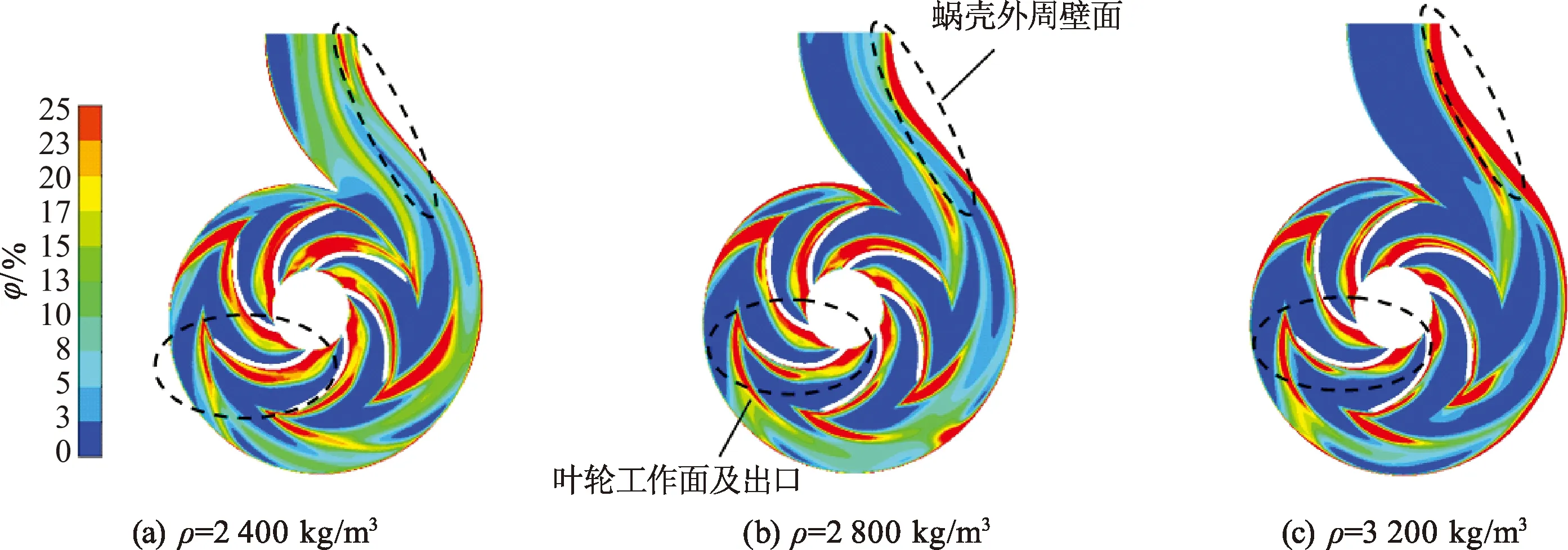
图7 不同颗粒密度下叶轮中间截面的固相体积分数分布

综上所述，颗粒密度、直径对流道颗粒体积分数分布的影响较为相似，颗粒质量主要受颗粒直径和密度影响，这也说明颗粒质量对碱液循环泵颗粒分布的影响规律.

图8为设计工况下，颗粒密度为2 800 kg/m3，颗粒直径为0.6 mm时不同颗粒体积分数下叶轮中间截面的固相体积分数分布.可以看出：随着固相体积分数的增大，叶轮内固相分布区域变化不明显，但高体积分数区域明显变大，颗粒间的相互作用加剧，颗粒与工作面的碰撞愈加强烈，导致叶片磨损加剧，且叶轮出口处工作面的颗粒尾迹愈加明显，这说明固相对液相流场的扰动变大；蜗壳流道内固相呈连续带状分布，固相颗粒愈加聚集，固液两相分离明显，带状条纹不断变宽.

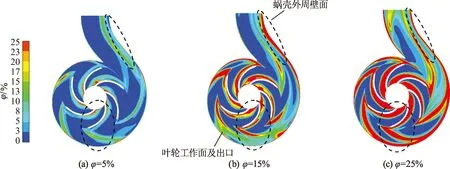
图8 不同颗粒体积分数下叶轮中间截面的固相体积分数分布

4 基于因子分析的回归方程

基于方差分析和残余诊断，剔除显著性不足的二阶交互作用，得到设计工况1.0Qd下输送不同颗粒属性的碱液循环泵扬程与效率的回归方程分别为

H=34.45+0.378d+34.46φ-0.000 226ρ-17.95dφ-0.016 6φρ，

(1)

η=81.19-0.949d+31.55φ-0.000 751ρ-0.027 8φρ.

(2)

回归方程的拟合精度除了通过代入原始数据进行对比验证外，还需要在区间内增加其他模拟试验点以检验其可信度.为了节省计算资源，综合考虑颗粒体积分数对泵性能的影响最大，在颗粒密度为2 800 kg/m3，直径为0.6 mm时，在体积分数5%～25%内增加2个体积分数值10%和20%进行数值计算，并将计算结果与回归方程预测结果进行校核，验证其在取样空间内的拟合精度，如图9所示.

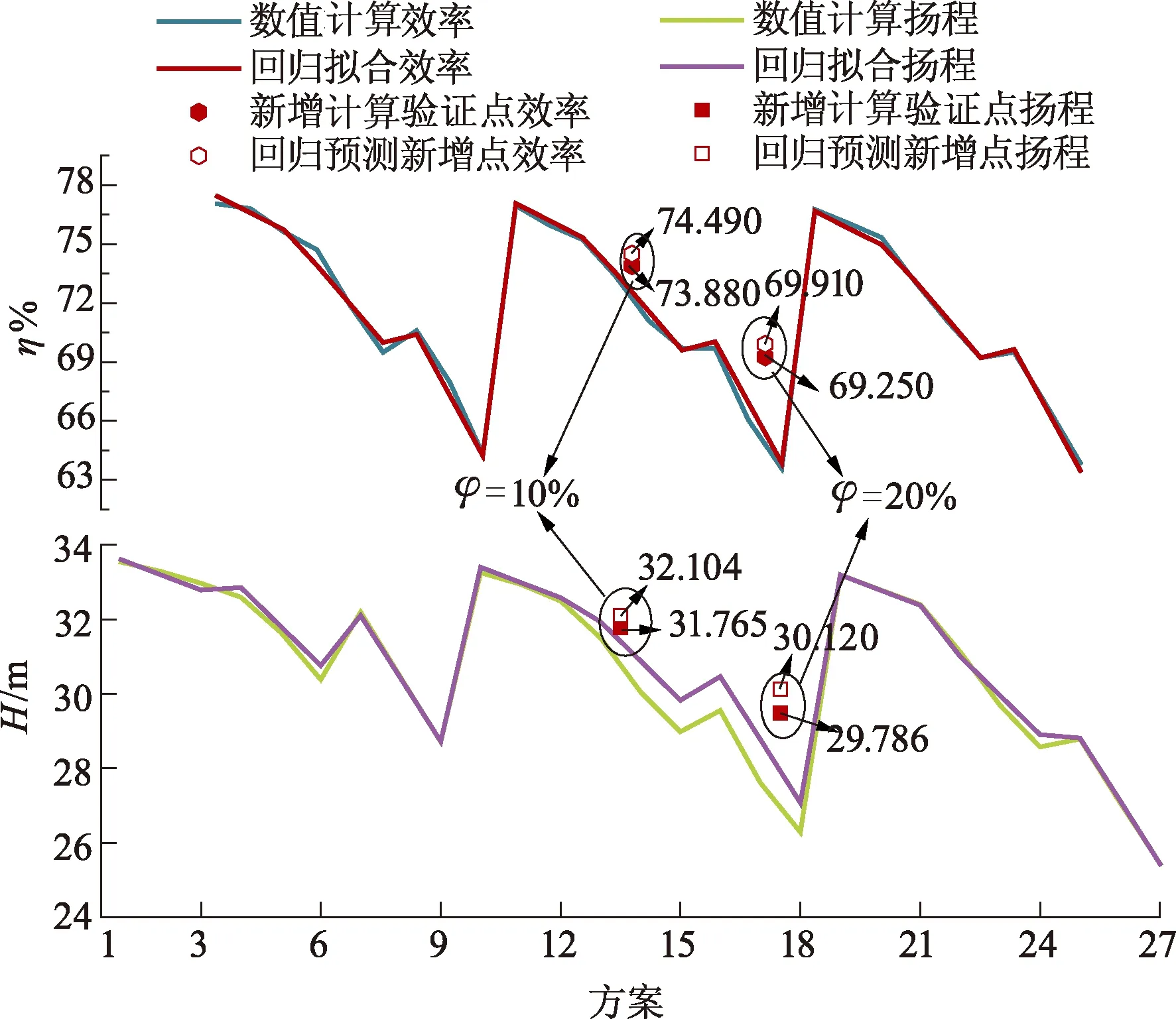
图9 因子试验数据及回归方程验证结果

由图9可以看出：通过对因子试验数据代入回归分析验证，发现27组数据效率拟合度较高；方案1—9的颗粒直径为0.2 mm，方案19—27的颗粒直径为1.0 mm，其拟合扬程和试验扬程误差小；方案10—18的颗粒直径为0.6 mm，其拟合扬程与试验扬程存在误差较大的点，最大误差为1.9%；从27组原始数值模拟试验数据与回归方程的求解值对比发现，总体拟合度较高；基于回归方程，新增的2个体积分数值10%和20%模拟试验点数值计算扬程与预测扬程的误差分别为1.05%和1.10%，效率误差分别为0.80%和0.94%，这说明回归方程预测精度较高，可信度较高.

5 结 论

1) 基于全因子试验与计算流体动力学方法相结合，分析了颗粒直径、体积分数和密度对碱液循环泵扬程与效率影响的显著性和相关度，发现颗粒体积分数、颗粒直径、颗粒密度、颗粒直径×颗粒体积分数、颗粒体积分数×颗粒密度对扬程有显著性，且依次增大；颗粒体积分数、颗粒密度、颗粒体积分数×颗粒密度、颗粒直径对效率显著性依次增大.

2) 颗粒直径与颗粒密度作为与颗粒质量相关的量，对流场的作用也较为相似，两者中任一参数的增大，均能导致叶轮内颗粒带状分布的区域有所减小，同时，颗粒愈加向叶片工作面和后盖板交界处迁移.颗粒体积分数的增大导致叶轮出口颗粒尾迹带较宽，且蜗壳流道中颗粒分布区域逐渐减小，固液两相分离较为明显，磨损位置变化不大，但磨损程度加深.

3) 建立了不同颗粒属性与碱液循环泵外特性相关的回归拟合模型，对碱液循环泵外特性进行了定量预测，效率和扬程拟合度较高，为碱液循环泵的水力设计提供了理论参考.