盲源分离中AMUSE算法的分离效果试验研究

张启明

摘 要：目前，盲源分离技术广泛应用于电子信号处理领域，但盲源分离中各算法的分离效果具有较大差异。对此，本文以盲源分离理论中的AMUSE算法为研究对象，通过MATLAB生成的周期性函数信号和随机收集的4种语音信号进行仿真试验，并选取相似系数作为AMUSE算法的评价准则。试验结果以及评价准则表明，AMUSE算法对信号的分离效果出色，且对噪声具有较好的鲁棒性。

关键词：盲源分离;AMUSE算法;信号处理;仿真试验

Abstract： At present， blind source separation technology is widely used in the field of electronic signal processing. but the separation effect of each algorithm in blind source separation is different. In this regard， this paper took the AMUSE algorithm in the blind source separation theory as the research object， and conducted simulation experiments through the periodic function signal generated by MATLAB and four randomly collected speech signals， and selected the similarity coefficient as the evaluation criterion of the AMUSE algorithm. The test results and evaluation criteria show that the AMUSE algorithm has excellent signal separation effect and good robustness to noise.

Keywords： blind source separation; AMUSE algorithm; signal processing; simulation experiment

1 基本理论

1.1 盲源分离

盲源分离（Blind Sources Separation，BSS）指的是在源信号未知的情况下，从观测到的信号中提取出各个初始源信号的过程，盲源分离中的“盲”主要表现为源信号未知、源信号之间的混合方式未知或者只知道少量的先验知识[1]。其中，“鸡尾酒会”问题（Cocktail Party Problem）是盲源分离中的典型问题，具体可以表述为：假设你参加了一个鸡尾酒会，在会场上有许许多多的声源，如宾客之间的谈话声（可能包括不同的语言）、酒会乐队的演奏声以及门外的噪声，如果此时在会场不同位置上有足够多的麦克风记录这些声音，那么每个麦克风所记录的声音信号即为会场内众多语音信号的混合信号。在事先不知道记录下哪些声音信号，也不知道麦克风位置的情况下，如何从麦克风收集到的混合信号中提取所需要谈话者的声音就是典型的盲源分离问题。

盲源分离最早可以追溯到20世纪80年代，当时是为了解决数字通信中线性单输入单输出（Single Input Single Output，SISO）统计信道的补偿问题而发展起来的多输入多输出系统（Multiple-Input Multiple-Output，MIMO）。HERAULT J完成了奠基性的工作，提出了H-J学习算法，并通过该算法将两个互不相关的源信号的混合信号分离开来[2]。

盲源分离的数学模型具体表述如下：在多输入多输出系统中，传感器观测到的信号如式（1）所示，要求找到一个逆系统，以得到原始的源信号，如式（2）所示，各源信号之间的混合方式未知。原理如图1所示，图中，[nt]表示噪声干扰信号;[Yt]表示经过分离矩阵W分离处理后的观测信号的近似信号;[W]表示为样点数。

因为盲源分离中“盲”的特性，需要做出一些假定来确保分离结果具有唯一解。假定如下：①源信号为平稳随机过程信号且至多只有一个信号服从高斯分布;②源信号矩阵中各个行向量相互独立;③混合矩阵[Α]为满秩矩阵。

1.2 AMUSE算法

Tong等人提出，当观测信号中的源信号具有非平稳随机的信号特性时，可以通过求解其相关矩阵的特征值达到盲源分离的目的[3]。该理论对应的盲源分离算法即为多源提取（Algorithm of Multiple Unknow Signals Extraction，AMUSE）。

AMUSE算法是一种典型的基于二阶统计量的盲源分离算法，在进行盲源分离时，除需要滿足盲源分离的基本假定外，必须对传感器收集到的观测信号进行预处理[4]。白化矩阵可通过求解观测信号自相关矩阵的奇异值得到。选取经白化处理后观测信号对应自相关矩阵时间延迟常数[τ]，对时间延迟常数[τ]的自相关矩阵进行奇异值分解，若时间延迟常数[τ]的自相关矩阵的奇异值各不相同，则通过两次奇异值分解即可成功构造出最终的分离矩阵W，进而完成盲源分离。AMUSE算法实质上是将复杂的信号处理问题转化为简单的矩阵计算问题。

本文选用盲源分离中较为经典的AMUSE算法，主要是因为AMUSE算法中关于时间延迟的自相关矩阵可以是观测信号的任意相关矩阵，可以是任何值，这样就相当于扩大了AMUSE算法的适用范围。因此，无论是非白信号还是平稳信号，都可以使用AMUSE算法分离。因为盲源分离并不知道观测信号的先验信息，因此在对观测信号进行AMUSE算法处理前，需要对观测信号进行数据的预处理。

1.3 盲源分离的算法评价准则

盲源分离算法的评价准则是衡量算法分离效果的重要依据，其中相似系数是较为常用且计算便捷的算法评价准则。相似系数是通过比较分离前后各信号之间的相似程度，进而以此为依据来衡量盲源分离算法好坏的一种评价准则[5]。

相似系数这种评价准则避免了因幅值不确定性带来的影响，可以客观真实地评价分离效果。若相似系数趋近于1，则可认为盲源分离的算法分离效果较好。

2 信号仿真试验

选用AMUSE算法作为分离算法，利用MATLAB软件工具进行信号仿真试验，仿真信号源分别为确定时序的随机函数信号和电脑收集的语音信号两种情况，并选取相似系数作为算法评价准则。

实例一：利用MATLAB编程语句随机生成3种确定时序的周期性平稳信号和平稳白噪声信号。3种确定时序的周期性平稳信号分别为周期为40的余弦信号、周期为20的正弦信号以及方波脉冲信号。平稳白噪声信号由一随机数列组成。源信号如图2所示。混合后的观测信号如图3所示，运用AMUSE算法对其进行分离，分离结果如图4所示。

在图2、3、4中，因为幅值是用来衡量波形的大小，故纵坐标幅值是没有单位的。

源信号与分离信号的相似系数分别为0.998、0.999、0.997、0.999，因相似系数的数值接近于1，说明AMUSE算法分离效果良好，且对噪声具有较好的鲁棒性;可以在噪声干扰下有效分离出混合信号中的噪声信号和3种函数信号。

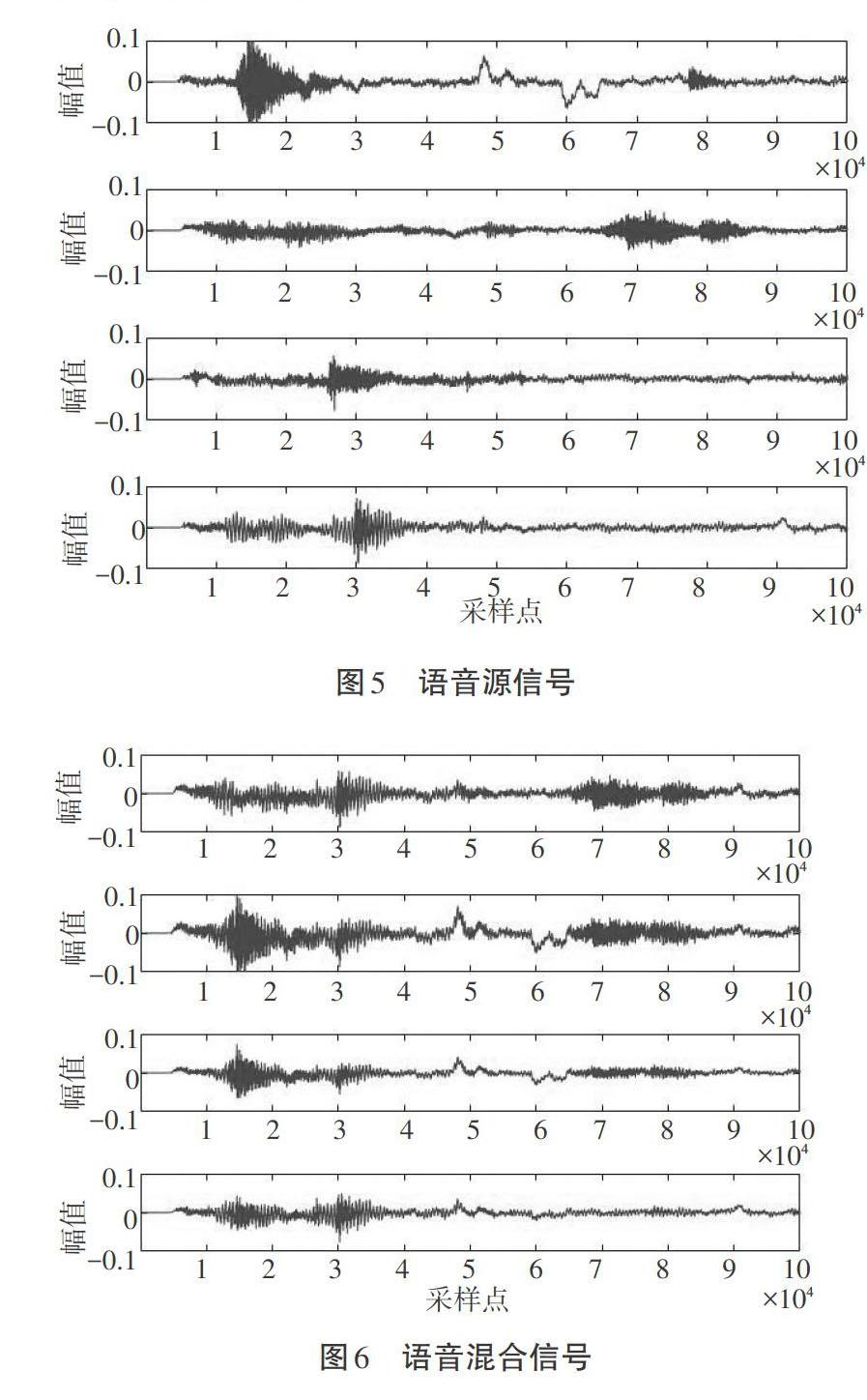
在图5、6、7中，因为幅值是用来衡量波形的大小，故纵坐标幅值是没有单位的。

源信号与分离信号的相似系数分别为0.921、0.919、0.9992、0.948，分离前后语音信号相似系数均在0.9以上，说明AMUSE算法对语音信号的分解效果良好，可将语音混合信号一一分离出来，得到初始的语音源信号。

3 结论

本文以盲源分离中的AMUSE算法为研究对象，通过MATLAB软件进行了两次信号仿真试验。试验一中分离前后的函数信号的相似系数最小值为0.9925，试验二中分离前后的语音信号的相似系数最小值为0.9198，均非常趋近于1，表明AMUSE算法的分离效果良好。

参考文献：

[1]张洪渊.信号源盲分离的理论与实验研究[D].上海：上海交通大学，2000：24.

[2]HERAULT J. Space and Time Adaptive Signal Processing by Neural Network Models.Neural Network for Computing[C]//AIP Conference Processing，1986.

[3]TONG L，LIU RW，SOON VC，et al. Indeterminacy and Identifiability of Blind Identification[J]. IEEE Transactions on Circuits & Systems，1991（5）：499-509.

[4]LANG T，LIU R.Blind Estimation of Correlated Source Signals[C]//Conference Record Twenty-fourth Asilomar Conference on Signals. IEEE，1990.

[5]黃艳波.单通道盲源分离算法的研究[D].杭州：杭州电子科技大学，2017：12.