可降解穴盘切割刀具优化设计与有限元分析*
胡双燕,胡敏娟
(农业农村部南京农业机械化研究所,南京市,210014)
0 引言
穴盘育苗技术是于20世纪70年代在欧美国家兴起的一项育苗技术[1],主要利用草炭、蛭石等轻基质无土材料做育苗基质,一穴一播的方式,完成一次性成苗的育苗任务。七五计划和八五计划将穴盘育苗技术列为农业部重点科技项目。市场上流通使用的苗穴盘主要是塑料穴盘[2],随着环保意识的逐渐增强,可降解穴盘应运而生,将可降解盘运用于蔬菜穴盘苗移栽过程[3],既能满足蔬菜育苗的各项需要,又能免去了穴盘回收的环节,不会污染环境。但是对于可降解盘的各项性质研究较少,与全自动移栽机配套使用的过程中存在一些问题,亟待解决。
可降解穴盘与全自动穴盘苗移栽机配套使用过程中,最重要的环节是完成可降解穴盘的切割分苗,为达到更好的单穴分苗效果,有必要对可降解穴盘进行切割使用的刀具进行更加深入的研究,我国关于刀具的研究文献中,对金属切割刀具的研究较多,对农业专用的刀具研究较少,农业生产上使用的切割装置的刀具类型主要有四种:第一种是用于免耕播种机中配合防堵装置使用的圆盘刀具[4],圆盘刀具切断覆盖于地面的秸秆,避免秸秆因缠挂在开沟器上或夹在两开沟器之间而造成堵塞。第二种是用于切割花生秧蔓与花生根盘的圆盘刀切割装置,与秧果兼收型花生联合收获机进行配套使用,可分离秧蔓和合理留茬高度的花生根盘。第三种是将锯齿型圆盘刀具作为木薯秸秆粉碎机切割装置的重要组成部分,充分发挥了锯齿型圆盘刀切割断面好,应用于秸秆的粉碎回收过程。第四种是盘刀铡草机切碎器中使用的刀具,方梅等[5]利用9Z-6A型盘刀式铡草机切割试验台,以主轴转速、动定刀间隙和秸秆含水率为试验因素,研究了盘刀铡草机的作业性能,为切碎器的研究和实际应用提供了理论数据。
近些年,我国蔬菜生产环节中机械化程度不断提升,切割刀具还被用于蔬菜生产环节中,柏宗春等[6]设计出用于切割蔬菜嫁接苗使用的高速切割装置,解决单株夹持切割效率低下的问题,与穴盘苗送盘装置相匹配,苗切割效率达到37 000株/h,能够满足嫁接流水线37个人工嫁接工位的用苗需求。为了研究不同环境条件下,切割植株时切削力差异,王丹丹等[7]选择水葫芦和花生作为水陆两种不同环境下,对比分析了削切、横切、斜切三种切割方式的切削力大小,通过分析不同作业环境条件下,刀具与外界条件的适应程度,为不同植物选择相适应的切割方式提供了参考。随着蔬菜生产环节的机械化程度不断提高,刀具的作用对象也不再是植株本身[8-10],研究用于可降解穴盘切割的刀具,才能充分发挥可降解盘的优势。能够完成可降解盘单穴分苗的切割刀具主要有直刃切刀和圆盘切刀两种类型,直刃切刀切割方向沿垂直于可降解盘盘口的方向自上而下进行切割,对于刀口的锋利程度要求严格,需要保证一次切割即可切断可降解盘之间的连接部分,由于可降解盘为正方形穴口,需将直刃切刀设计为三面刀才可完成对可降解盘单钵的分割,对刀具的设计精度要求较高。其次在移栽机送盘位置安装刀具,需要预留直刃切刀的行程距离,比圆盘切刀需要更多的安装空间。
因此,本文选择圆盘切刀进行可降解盘切割时的受力情况,优化刀具的结构,研究圆盘刀具齿数、刃口形状等因素对可降解盘切割效果的影响。由于人工计算圆盘刀具的应力、应变较为繁琐,采用有限元软件ANSYS对圆盘刀具进行应力分析计算,获得圆盘刀具的应力分布图和模态分析图,为用于切割可降解盘的圆盘刀具的优化和设计提供理论依据。
1 建立圆盘刀有限元模型
本文先通过Soildworks建立表1中圆盘切刀的实体模型,将其保存为Parasolid(*.x_t)格式,然后导入ANSYS workbench软件。考虑到圆盘刀具切割可降解盘的实际情况,圆盘刀具需保证一定的耐磨性和锋利程度,其材料选择AISI类型A2刀具钢,按照表2中的数据在ANSYS workbench中设置相应的基本材料属性。

表1 圆盘刀具规格表Tab. 1 Disc cutter specification table

表2 基本材料属性表Tab. 2 Basic material properties
圆盘刀具的形状结构比较简单,选择网格划分方法确定为Hex Dominant,Hex Dominant划分方法可以将划分为主要部分和次要部分,主要部分刀刃部分的划分比次要部分刀面部分的划分更细致,有利于仿真分析,如图1所示。

(a) 24齿单刃圆盘刀网格划分图 (b) 24齿双刃圆盘刀网格划分图 (c) 36齿单刃圆盘刀网格划分图
图1为圆盘切刀的网格划分图,网格单元为8节点的六面体网格单元,六面体单元的计算精度明显要高于四面体单元,在实体离散过程中,采用相同大小的单元尺寸,六面体网格划分的单元数量要比四面体网格划分的单元数量少得多。较少的单元数量意味着较少的有限元计算时间,会让计算求解过程更加便捷。
2 圆盘切刀受力分析与计算
2.1 圆盘切刀受力分析
圆盘刀具在完成网格划分,对其施加载荷和约束,首先对圆盘刀具进行受力分析,圆盘刀具中间由驱动轴带动进行转动切割可降解盘,圆盘刀具会存在离心力F,如图2所示。
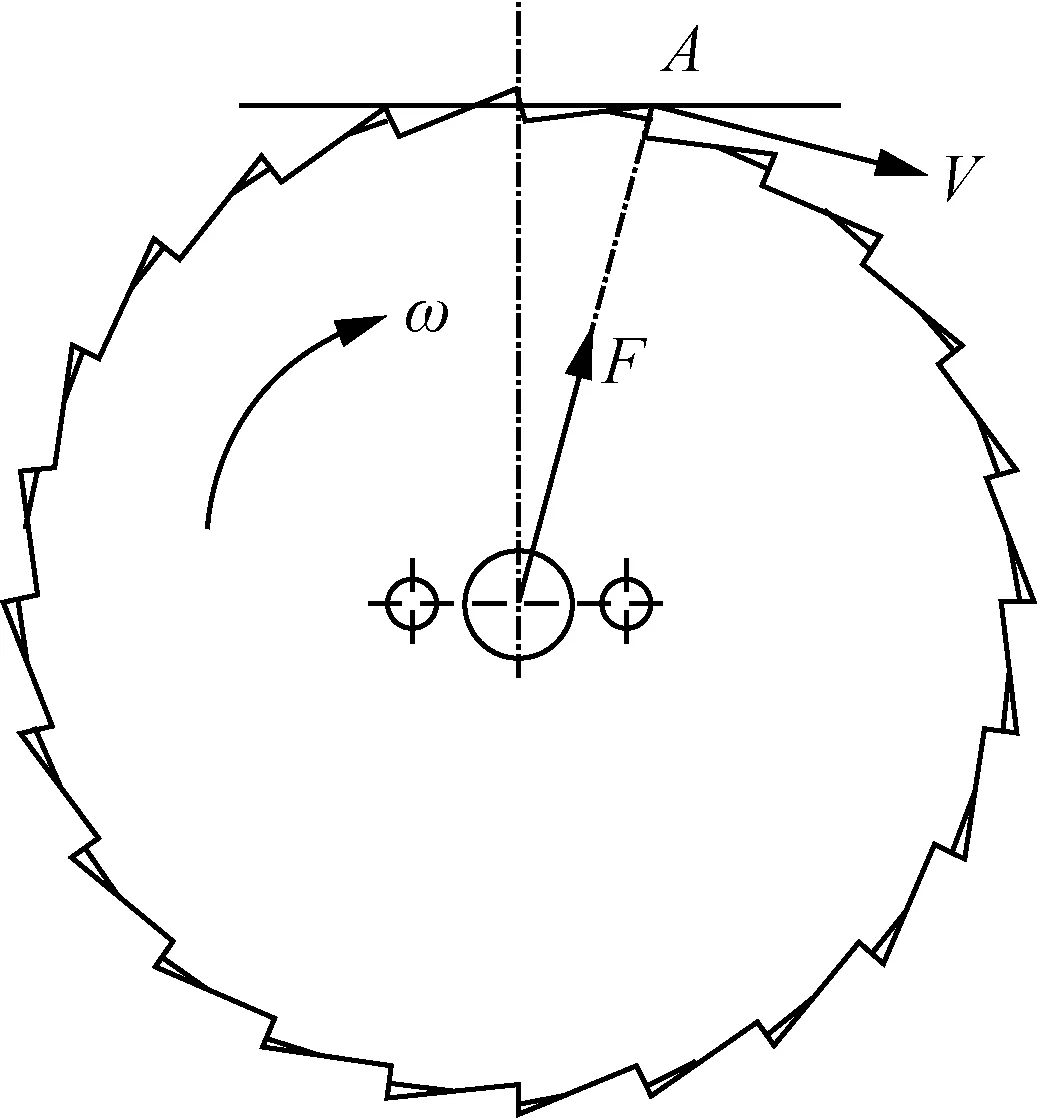
图2 圆盘刀具受力示意图
根据离心力计算公式
(1)
式中:m——圆盘刀具的质量,kg;
ω——圆盘刀具的角速度,rad/s;
r——圆盘刀具的半径,m。

(2)
式中:ρ——圆盘刀具的密度,kg/m3;
h——圆盘刀具的厚度,m;
n——电机转速,r/min。
结合切割可降解穴盘过程中对刀具刚度的要求以及刀具的安装空间,拟定刀具钢的密度和圆盘切刀的厚度和半径,依据辣椒穴盘苗移栽机分切的工作效率拟定圆盘切刀的转速。分别将ρ=7 860 kg/m3,h=1.5×10-3m,r=7.5×10-2m,n=300 r/min代入式(2)中,可以求得离心力F=10.266 N。
2.2 圆盘切刀刃口受力分析
因为在可降解盘切割过程中,刀片刃口受到的来自可降解盘的压力为正压力,如图3所示,可以通过对其施加正压力,随着刃口正压力的变化分析刀片刃口的应力变化和变形变化以及位移量。

(a) 单刃刃口受力示意图 (b) 双刃刃口受力示意图
根据实际移栽作业情况,圆盘切刀的刀轴转速大约为300 r/min,可降解盘与塑料盘相比硬度较软,吸水性能较好,因此会随着育苗过程的进行逐渐变软,圆盘刀具受到可降解盘对其施加的正压力很小,为了对圆盘刀具进行仿真分析,可将F1、F2的数值设置为1 N。如图4所示,在ANSYS的workbench模块中的set up界面中对刃口施加1 N的正压力,对圆盘刀本身施加一个300 r/min的转速,利用solution求解出圆盘刀具的应力、应变情况。

图4 施加载荷的有限元图形
3 ANSYS静力学仿真分析结果
对圆盘切刀进行静力学仿真分析,通过图5中的应力、应变分布云图找到圆盘切刀的薄弱环节,分析圆盘刀具的变形规律。通过表3、表4中圆盘切刀应力与应变的最大值和最小值,与其自身强度进行比对,并找到能满足切割可降解穴盘作业的圆盘切刀的最佳组合方式。

(a) 24齿单刃圆盘切刀应力云图 (b) 24齿双刃圆盘切刀应力云图 (c) 36齿单刃圆盘切刀应力云图

表3 最大与最小应力值表Tab. 3 Maximum and minimum stress values table

表4 最大与最小应变值表Tab. 4 Maximum and minimum strain values table
由图5中不同类型的圆盘切刀的应力云图可以得到以下共性规律:沿直径从中心孔向外,圆盘切刀所受到的应力逐渐增大,在与可降解盘接触的刃口加载面处应力值达到最大值,应力最大值集中于刃口加载面周围,圆盘切刀的应力最大值与最小值相差较大。
由表3的应力数据可知,对不同刃数的刀具进行对比分析可知,双刃圆盘切刀明显受到的最大应力比单刃圆盘切刀要小很多,如24齿的单刃圆盘切刀最大应力为3.802 7×105Pa,24齿的双刃圆盘切刀的最大应力为1.658 4×105Pa。对不同齿数的圆盘切刀进行对比分析,36齿的单刃圆盘切刀的最大应力数值为3.139 9×105Pa,是单刃圆盘切刀中所受到的最大应力最小;24齿双刃圆盘切刀是双刃圆盘切刀中所受到的最大应力最小,只有1.658 4×105Pa。通过表4中的应变变化可以看出,各种类型的圆盘切刀的应变都比较稳定,稳定在10-7~10-6这一数量级,其中24齿双刃圆盘切刀的最大应变值为8.350 2×10-7m/m,为六种圆盘切刀中的最小值。
4 齿数与刃口形状对应力、应变的影响
4.1 试验因素
根据有限元静力学仿真得到六种不同齿数、刃口形状的组合形式下的圆盘切刀的最大应力、应变数值,运用Design-Expert软件考察齿数、刃口形状对圆盘切刀的应力、应变的影响情况。表5为因子水平表,齿数为三水平因子,刃口形状为二水平因子,采用混合水平正交试验设计方法。

表5 因子水平表Tab. 5 Factor level table
4.2 试验方法与评价指标
根据表5因子水平表中一个二水平因子,一个三水平因子,选用混合水平正交表L18(2×37)为本次试验选用的混合正交试验设计表,如表6所示,其中第一列为二水平因子,第三列为三水平因子。

表6 试验设计与结果Tab. 6 Experimental design and results
4.3 试验结果与分析
表6中A、B分别为因素编码值,1、2、3分别为水平编码值,采用Design-Expert10.0.7对试验数据进行处理与统计,对试验结果在置信度为95%的条件下,进行F检验。由表7、表8可知圆盘切刀齿数、刃口形状对最大应力、最大应变都表现为极显著,同时失拟项不显著,证明所选模型适当。
试验指标(最大应力y1)与试验因素(齿数、刃口形状)之间的回归模型方程如式(3)所示。
y1=-1.079×105A-1.186×105B-
8.448×104B2+3.916×105
(3)

表7 最大应力方差分析Tab. 7 Variance analysis of maximum stress
试验指标(最大应变y2)与试验因素(齿数、刃口形状)之间的1回归模型方程如式(4)所示。
y2=-5.400×10-7A-5.928×10-7B-
4.259×10-7B2+1.965×10-6
(4)
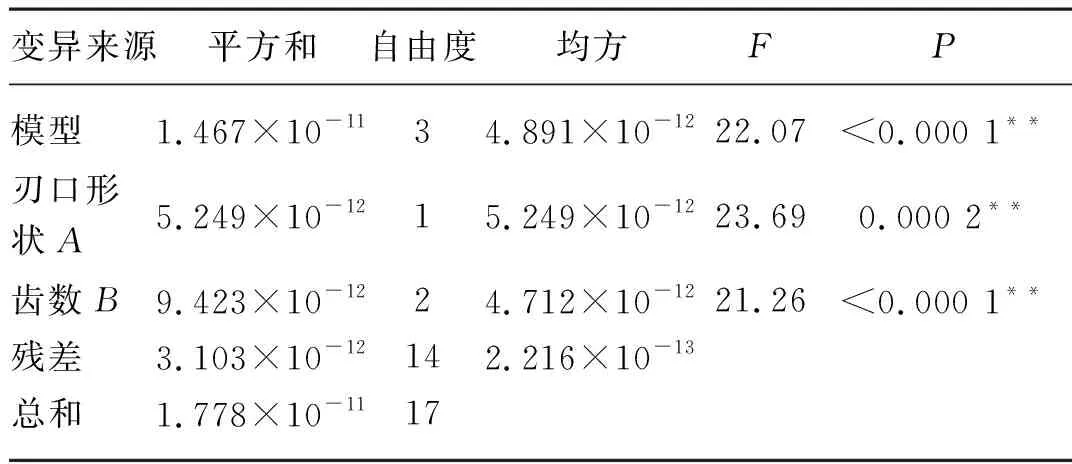
表8 最大应变方差分析Tab. 8 Analysis of variance of maximum strain
4.4 各试验因素对试验指标的影响效果
图6反映出圆盘切刀齿数、刃口形状(单、双刃)对最大应力、最大应变的影响效果,二者的基本变化趋势保持一致。
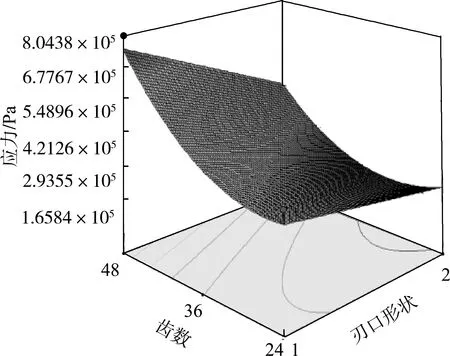
(a) 应力与齿数、刃口形状之间的响应曲面
当刃口形状保持不变时,随着圆盘切刀的齿数逐渐增加,最大应力、应变的数值逐渐增大;由于刃口只有单、双刃两种类型,当圆盘切刀齿数保持不变时,双刃圆盘切刀比单刃圆盘切刀所承受的最大应力、应变小。综上所述,在24、36、48三种齿数的单双刃圆盘切刀类型中,最佳选择是最大应力、最大应变都为最小值、加工难度较为容易的24齿双刃圆盘切刀。
5 圆盘切刀模态分析
圆盘切刀在进行切割作业过程中是时刻承受着动态载荷的,而模态分析是为结构动力特性的优化设计提供依据,ANSYS静力学仿真分析确定圆盘切刀的最佳组合为24齿双刃圆盘切刀。运用ANSYS WORKBENCH对圆盘切刀进行模态分析,通过模态分析研究振型和固有频率[11]。圆盘切刀的共振频率中低阶的固有振动比高阶振动对结构的振动影响大,不需要对全部的振型进行分析计算,只需要计算前10阶即可。
5.1 模态分析原理
刀具的模态分析主要包括:建立模型、加载求解、扩展模型、观察结果四个部分组成[12]。
一个具有N个自由度的线性振动系统,若不计阻尼的影响,则其自由振动的运动微分方程一般形式可以表示
[M]{X}+[K]{x}={0}
(5)
设(5)方程的解为简谐振动,即
{x}={X}eω t
(6)
式中: {X}——各点的振幅;
[M]——系统质量矩阵;
[K]——系统刚度矩阵;
t——时间,s。
代入式(5)~式(6)中,得到
([K]-ω2[M]){x}={0}
(7)
当[K]、[M]为正定矩阵时,可以求得对应的N个ωr2的值,分别为1阶,2阶,…,N阶固有频率[13]。
典型的无阻尼模态分析求解方程
([K]-ω2[M]){φ}r={0}r=1,2,…,N
(8)
式中: {φ}r——模态[14]。
5.2 建模与施加约束
模态分析使用的三维实体模型与静力学分析使用的实体模型在材料属性、实体参数等方面都相同,网格划分方法依旧选择Hex Dominant方法。
模态分析中求解自由模态和约束模态的结果是不同的,根据本次试验需要采用求解约束模态[15]。实际工作状态下,圆盘切刀只绕着中心轴转动,因此对其他5个自由度进行限制,即3个不同方向的表面约束:X(切向)、Y(径向)、Z(某一轴向长度)的位移均为零,旋转自由度进行约束MX,MY均为零,Z轴为中心轴,设置为free。
5.3 模态分析结果
圆盘切刀模态分析的前10阶固有频率如表9所示。图7各阶振型图中第1阶的振动频率为0,第2阶开始产生振动,第2、3阶振动频率不高,主要产生的振型为从中心轴沿圆盘切刀径向发生轻微振动,圆盘切刀的整体振型未发生明显变化。第5、6阶振型振动频率逐渐升高,圆盘切刀的振型发生明显的形状变化,主要表现为沿切向90°划分为4部分,频率由边缘开始沿径向逐级递减,最小频率由圆盘切刀中心向周围呈“十”字形分布。第7、8阶振型出现沿切向呈60°划分为6部分,频率也是出现由边缘向中心沿径向逐级递减的现象,最小频率由圆盘切刀中心向周围呈“*”形分布。第9、10阶振型则呈现出沿切向呈45°划分为8部分,频率由边缘开始沿径向逐级递减的现象,最小频率由圆盘切刀中心向周围呈“米”字形分布。
圆盘切刀的第1阶固有频率为0,为刚体振动可不予考虑,根据频率与转速之间的关系公式
(9)
式中:f——频率,Hz;
p——电机极对数,对。
表9中第2阶固有频率为202.7 Hz,为最小固有频率,实际工作时的圆盘切刀的转速不低于300 r/min,一般电极对数为1时,同步转速是3 000 r/min;电极对数为2时,同步转速是1 500 r/min;电极对数为3时,同步转速是1 000 r/min,这些转速与本次研究所需的300 r/min 的转速相比过大,转速无法相匹配。综上所述,选择电机极对数为4[16],属于八级电机,它的同步转速是500 r/min,电机的额定转速不仅与同步转速有关,还与电机的转差率有关,一般电机的额定转差率为4%~6%,可以保证电机的额定转速始终大于300 r/min。经过式(7)换算,可以得到频率为33.4 Hz。202.7 Hz>33.4 Hz,明显低于圆盘切刀的最小固有频率,圆盘切刀的模态频率高于实际工作时的频率,这说明刀具在按照固有振型振动时,与移栽机送苗工作装置发生共振的可能性很小。
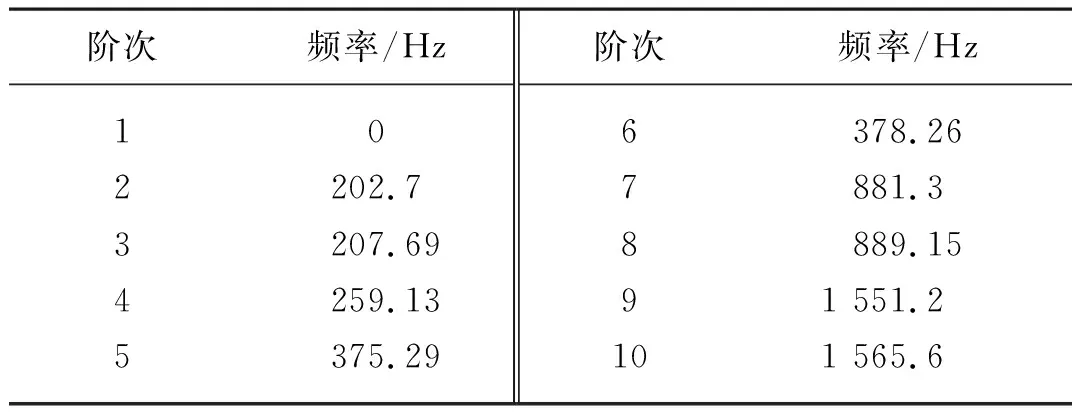
表9 圆盘切刀模态分析的前10阶固有频率表Tab. 9 First 10 order natural frequencies of the modal analysis of the disc cutter
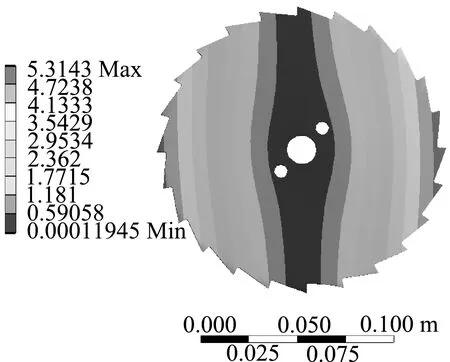
(a) 圆盘切刀第2阶振型 (b) 圆盘切刀第3阶振型 (c) 圆盘切刀第4阶振型
6 切割试验
6.1 材料与方法
为验证仿真结果的合理性,2021年3月在溧阳进行24齿双刃圆盘切刀对可降解盘的切割效果的实验,试验主要材料为图8所示的72穴可降解穴盘。图9为圆盘切刀切割作业情况,为更好的模拟圆盘刀具的实际工作情况,将穴盘中放置一定体积的黏土和假苗代替实际穴盘中的基质和移栽苗,保证与移栽作业中相似的秧苗的苗高与姿态。

图8 72穴可降解穴盘

图9 圆盘刀切割作业图
将圆盘刀具安装在移栽机的分苗装置上,每组7个刀盘,由一个电机统一带动,具有相同的转速。根据实际移栽工作需要,刀轴转速保持在300 r/min左右,保证圆盘切刀作业有充分的安全性与稳定性,试验过程中选择的转速会比实际需要的转速偏大一些,这样对圆盘刀的各项性能要求更高。本次试验选择的电机转速分别为350 r/min、400 r/min、450 r/min,在不同转速下进行可降解盘的切割试验,每种转速下切割重复次数为72次(一张穴盘),并记录切割效果。
6.2 结果与分析
本次试验主要是检验24齿双刃圆盘切刀对可降解盘的切割效果,切割效果可以分为三种,如图10所示。

(a) 切口整齐 (b) 切口偏移(偏移角度小于7°)
图10(a)和图10(b)均为完成切割工作,属于切割合格,图10(c)属于切割不合格。不同转速下的切割效果如表10所示。
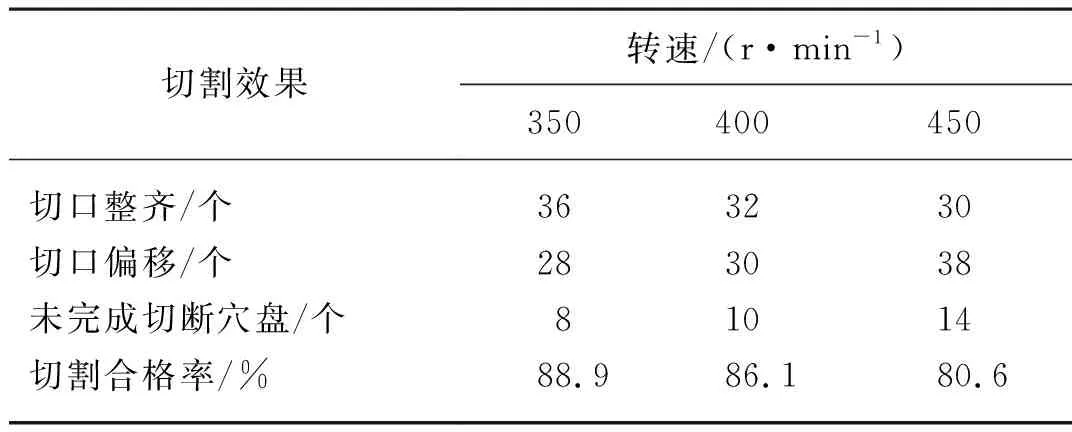
表10 不同转速下的切割效果Tab. 10 Cutting effect at different rotating speeds
表10中记录350 r/min、400 r/min、450 r/min转速条件下24齿双刃圆盘切刀的切割效果。根据不同转速下实际切割效果进行分析:随着转速增大,切割合格率逐渐降低,分别为88.9%、86.1%和80.6%。刀轴转速越大,越容易出现切割偏斜的现象,切割质量越难保证。通过试验发现,越先进刀的部分切口越整齐,整张穴盘的前半部分切割质量优于后半部分。24齿双刃圆盘切刀在350 r/min、400 r/min、450 r/min的刀轴转速下,圆盘切刀均能保持较好的切割稳定性,未出现刀具横向振动、滑移等现象。
7 结论
本文主要研究了用于可降解穴盘单穴切割分离的圆盘切刀的受力情况,运用ANSYS软件对圆盘切刀进行静力学仿真与模态分析,研究圆盘刀具齿数、刃口形状等因素对可降解盘切割效果的影响并进行了不同刀轴转速下的切割试验,得到以下结论。
1) 圆盘切刀在切割作业过程中,整排圆盘切刀由电机带动,刀轴转速不低于300 r/min,且每片刀片保持相同大小的转速与转动方向,这样会产生沿着刀刃切线方向的大小相等的离心力。通过对24、36、48三种齿数的单双刃圆盘切刀进行ANSYS静力学仿真分析,比较上述六种不同组合形式的圆盘切刀在极限载荷和约束条件下的应力、应变情况,确定圆盘切刀的最佳组合方式为24齿双刃圆盘切刀,切刀受到的最大应力为1.658 4×105Pa,本次研究选用的刀具材料为A2刀具钢,屈服强度可达700 MPa,远大于切刀所受最大应力,因此圆盘切刀强度储备充足。
2) 根据仿真分析的结果和得到的试验数据,运用混合水平正交试验设计的方法,以圆盘切刀刃口形状(单、双刃)、齿数为试验因素,以圆盘切刀受到的最大应力、最大应变作为试验评价指标,运用Design-Expert软件得到回归模型和试验因素响应曲面,得到圆盘切刀的最优组合为24齿双刃圆盘切刀,与静力学仿真分析的结果一致。
3) 对24齿双刃圆盘切刀进行模态分析,求解约束模态,得到圆盘切刀最小固有频率为202.7 Hz。实际圆盘切刀工作时转速不小于300 r/min,根据圆盘刀固有频率与转速的关系,求出额定工作频率为33.4 Hz,说明了圆盘切刀正常切割可降解盘作业时的额定工作频率远低于圆盘切刀本身的最小固有频率,验证了圆盘切刀正常切割可降解盘作业时的额定工作转速远低于其发生共振的临界转速,发生共振的可能性很小。
4) 24齿双刃圆盘刀在切割试验过程中的切割合格率可以达到80%以上且能保证作业的稳定性和可靠性。

