考虑平抑电压波动的交直流配电网储能优化配置

郭 沛

考虑平抑电压波动的交直流配电网储能优化配置

郭 沛

（国网河南省电力公司，郑州 450000）

为解决目前配电网中日益增加的新能源出力造成的功率波动问题，本文提出一种考虑时间和空间特性的平抑交直流混合配电网系统功率波动的最优储能配置方法。首先确立发电消纳及潮流、风机和光机等约束的数学模型，利用交替迭代法计算交直流混合配电网潮流，然后通过快速非支配排序遗传算法（NSGA-II）对模型进行求解，最后输出结果为最优解与其他可行解的优化指标对比图。通过储能系统优化配置，配电网偏差值与网络损耗都明显减小，验证了所提出的利用最优化储能系统配置平抑新能源发电并网产生波动方法的可行性。

交直流配电网；多目标优化；储能系统配置；波动平抑；电压偏差值和；网络损耗

0 引言

分布式风力发电及光伏发电，由于其本身具有间歇性与波动性，不能进行精确预测，将该类新能源大量接入配电网增加了系统运行的安全隐患，因此需要对其产生的功率波动进行有效的平抑[1-4]。储能技术的不断突破为风电与光电并入配电网提供了一种较好的技术选择，利用电池储能系统可实现风力发电和光伏发电的出力在时间坐标上的平移，通过切换充电状态和放电状态，达到负荷需求的“削峰填谷”效果，改善能量间歇性，提高配电网安全性。储能技术有望解决新能源发电并网引起的一系列安全问题，提高新能源并网效益。

考虑如何在交直流混合配电网中加入同样条件的储能装置以获得最好的平抑效果，是研究储能系统优化配置的重点。为此，国内外学者对多储能交直流配电网系统的设计与控制进行了大量研 究[5-11]。文献[12]将可控负荷视为虚拟储能，提出一种蓄电池和虚拟储能进行协调控制的策略，通过设置不同的滤波常数分别抑制联络线功率中高频和低频部分，但该文献所研究的虚拟储能仅限于电热泵群体，并没有涉及更多负荷领域。文献[13-15]详述了交直流混合微电网的拓扑及各种电子设备的配置方式，提出了基于不同运行模式间的迅速切换控制策略，不足之处是没有考虑分布式电源的二次协调控制与应用。文献[16-17]是利用储能系统中的电容和蓄电池分别抑制系统功率高频波动和补偿低频波动，能够满足配电网的电能质量要求和负荷功率需求，但需额外增加滤波器，且会减少蓄电池的寿命，因此经济性较差。文献[18-19]采用电压分层控制策略延长蓄电池的使用寿命，但若满足储能系统工作的电压值，则会导致该线路的电压偏离额定值较多。

针对上述文献中涉及的储能系统与交直流混合配电网无法高效配合运行的问题，本文提出一种实现最优化平抑交直流混合配电网风光波动的储能系统优化配置方法，从满足配电网高效率且安全运行等方面综合考虑，进行储能系统的优化配置。

1 数学模型

1.1 目标函数

通过节点的电压偏差值和线路间的网络损耗能直观体现出交直流混合配电网运行性能。为最大程度地降低配电网的网络损耗，以及降低储能系统调控时产生的配电网电压波动，保证配电网的安全运行，以系统网络损耗最小与配电网节点电压偏差最小为优化目标。

1）网络损耗之和

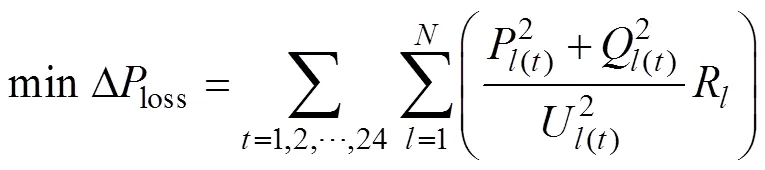
式中：为线路条数；P(t)和(t)为时间段内线路的有功功率与无功功率；U(t)为此时线路的平均电压；R为线路的电阻值。

2）电压偏差值之和

式中：为配电网节点个数；Ua(t)为节点在时间段补偿后的电压幅值的平均值；U(t)为节点的电压标准值幅值；ni为配电网节点的电压额定值。

1.2 约束条件

1）潮流约束

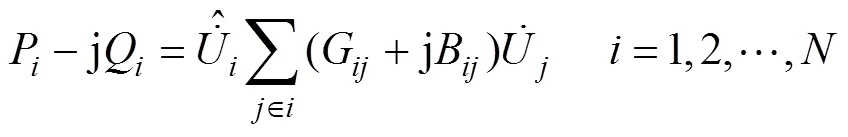
2）线路功率约束

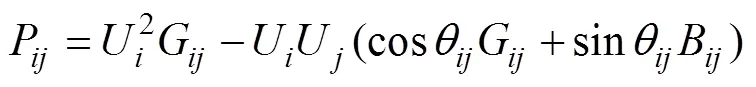
式中：P、分别为线路（节点和组成）的有功损耗和无功损耗；U和U为节点和的电压；为U和U的相位差。

3）节点电压约束

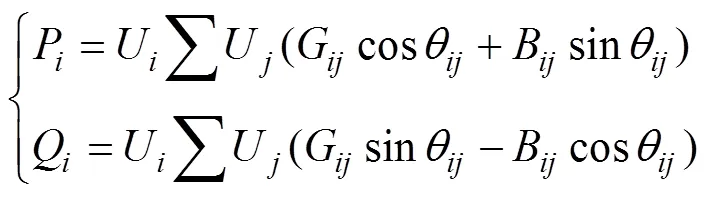
4）风机出力约束

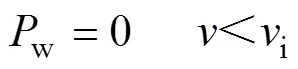
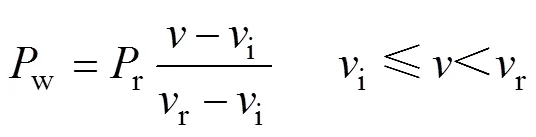
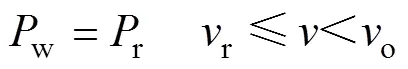
式中：r为风机输出的额定有功功率；i、r和o分别为切入风速、额定风速和切出风速。

5）光伏出力约束

光伏电机时刻的实际出力P为

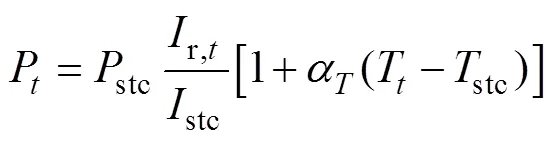
式中：stc为标准条件下（太阳辐射强度stc= 1 000W/m2，温度stc=25℃）光伏板的出力；为光伏板的功率温度因数；r,t为时刻实际的太阳辐射强度；T为时刻光伏板的温度。某风机发电和光伏发电日出力典型特性曲线如图1所示。

6）储能出力约束

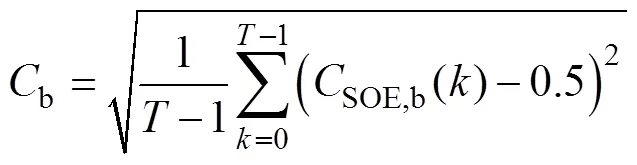
式中：Cb为平抑风力发电与光伏发电波动过程中储能能量状态与充放电最大能力CSOE（其最小值CSOE,min= 0.5）的方均根值。储能系统出力典型特性曲线如图2所示。通过在操作点1和操作点2的切换，可以在不同时刻分别将储能等效为稳定出力的电源和负荷。

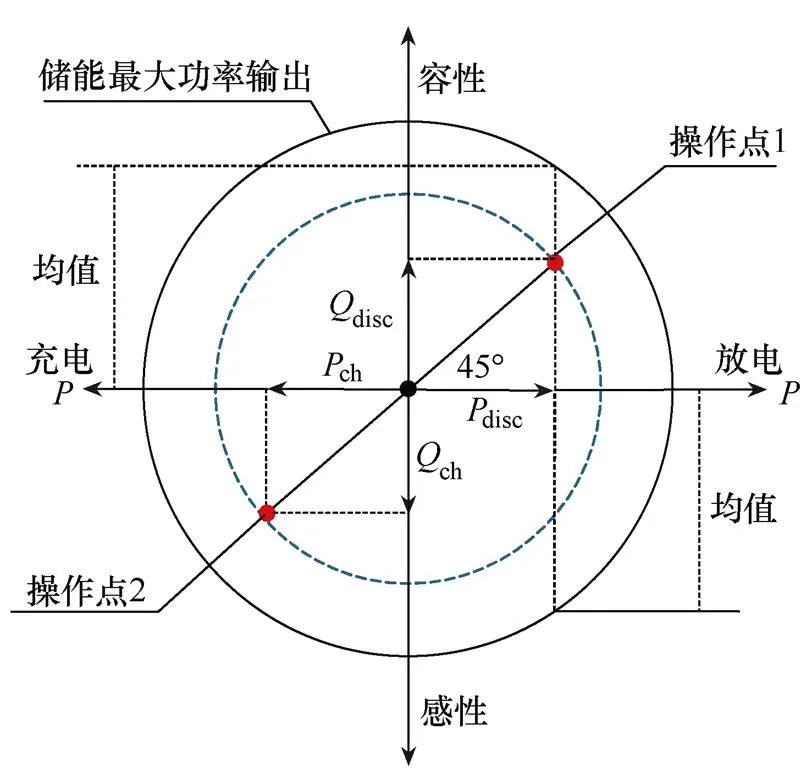
图2 储能系统出力典型特性曲线

本文在传统潮流计算基础上，将风机和光伏的约束条件考虑在内，使得该模型的精度进一步得到提升。但是难点在于如何利用算法在众多可行解中得到两个目标函数（网络损耗最小与配电网节点电压偏差和最小）的最优解。

2 基于非支配排序遗传算法的模型求解

本文采用快速非支配排序遗传算法（non- dominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ）计算Pareto前沿，通过协调各个目标，使各个目标尽量达到令人满意的Pareto最优解集。算法的主要思想是利用非支配排序算法对种群进行非支配分层，然后计算虚拟适应度再进行选择、交叉和变异操作，最后执行精英保留策略。这样能够保证整个算法在不停搜索Pareto最优解集的同时，保持种群的多样性和避免优秀个体的流失，还提高了整个算法的全局收敛性和计算效率[20]。

运用NSGA-Ⅱ可以很好地处理两个目标函数不能同时达到最优时如何选择最优解的问题，因此本文选择使用该算法进行模型的求解。利用NSGA-Ⅱ进行交直流混合配电网储能系统优化配置流程如图3所示。

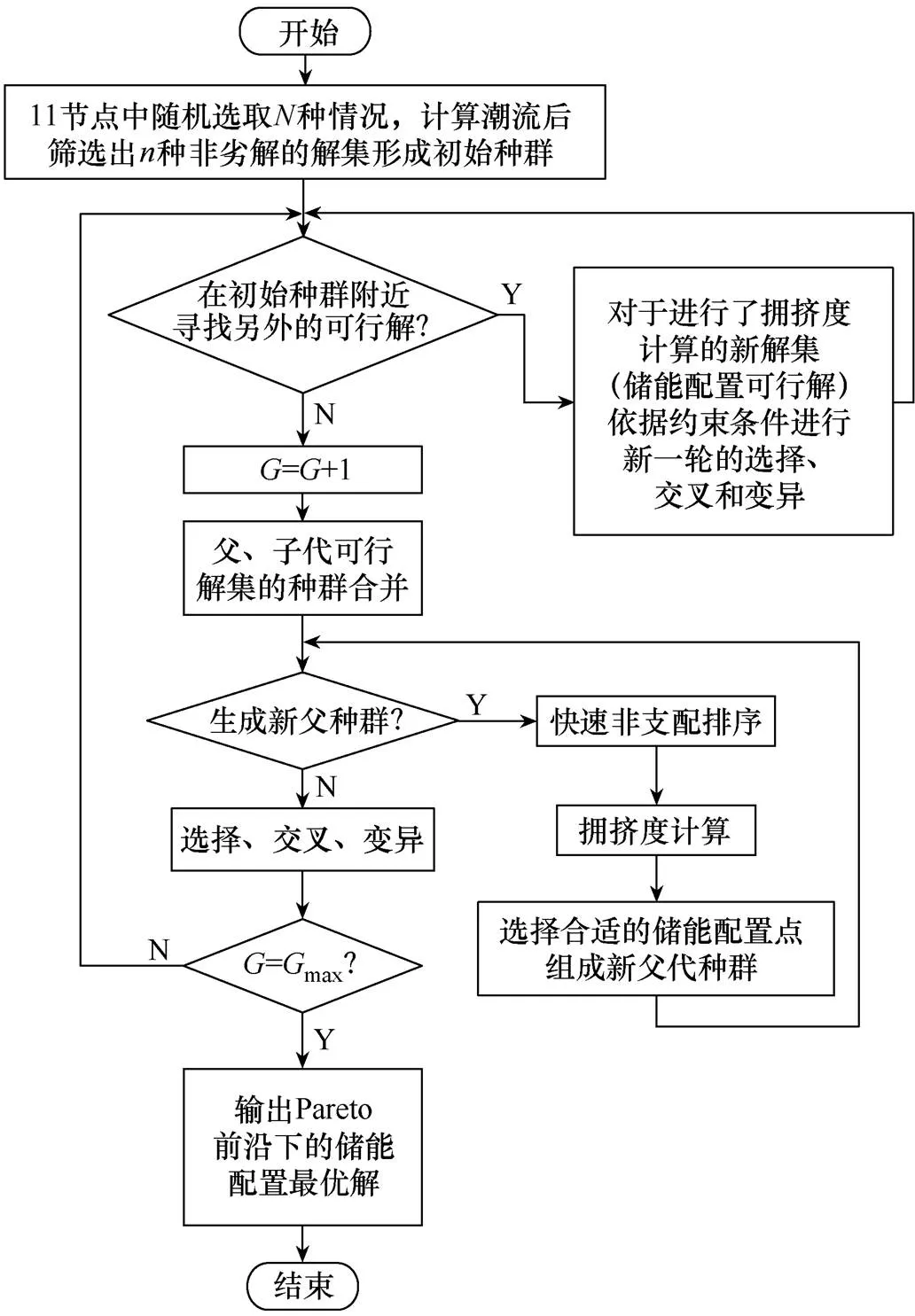
图3 储能系统优化配置流程

1）假设参与调控的储能装置为3台同容量、同型号、同功率的电池储能系统（battery energy storage system, BESS），且每一个节点最多存在一台。在11节点中随机选取种情况，每种情况下某时间内在某节点将储能装置加入该节点进行调控，计算调控后的交直流混合配电网潮流，依据约束条件筛选出种非劣解的解集后，即生成了初始的种群。

2）在初始种群（节点和时间）附近寻找另外的可行解（如节点2相关联的节点3，时间上13h附近的14h等），对生成的新解也依据约束条件进行新一轮的筛选后，选出第一代种群的非劣解，将第一代种群选出的非劣解与初始种群的解进行合并，合并后的种群为第二代种群，此时种群规模达到2。通过快速非支配排序法对其排序，并且计算排序结果中处于同一等级的对象的拥挤度（例如节点7在15h时附近的非劣解数目大于节点7在9h时的非劣解数目，则可认为前者拥挤度高于后者），依据个体的拥挤度及它们之间的非支配关系得到新的父代种群，此时新的父代种群的规模为。

3）对于新的父代种群重复步骤2），使进化朝着非劣解均匀分布（即趋近于某几个节点，某几个时间）的方向进行，当种群的选择、交叉和变异依次循坏直到父代种群迭代达到预设的最大值时，则跳出该算法循坏。

4）该算法最后一次迭代生成的种群中，非支配排序等级为1的解组成一个集合，使用模糊理论从该集合中选择一个最优解。预先设定好两个目标函数（电压偏差值和与网络损耗）的最大值与最小值，计算出每个Pareto解中相应目标函数的满意度m，所有满意度中的最大值max就是所求的最优解（储能系统的配置节点与开关断时间），可以根据人为需求调整电压偏差值和与网络损耗的极值区间，从而得到想要的折中最优解。

3 算例仿真

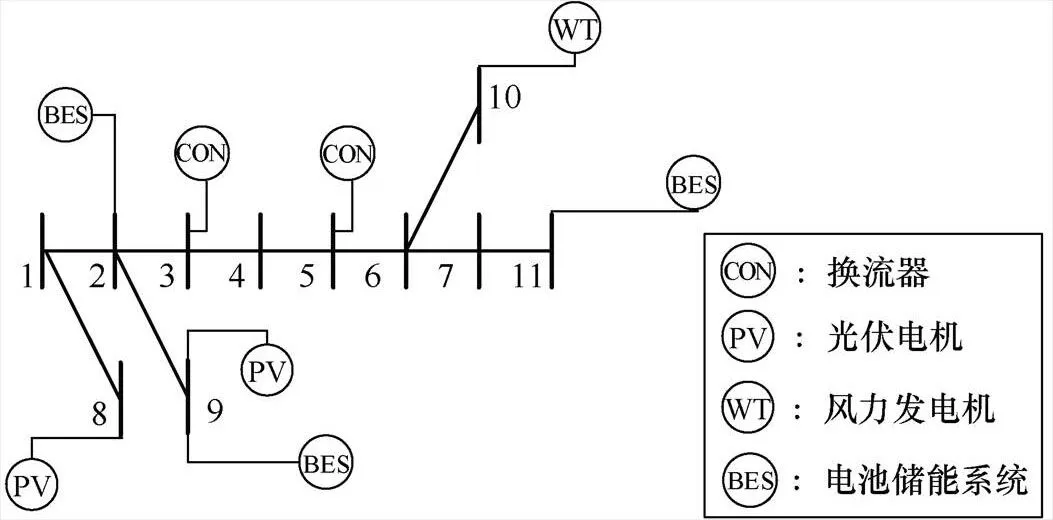
图4 11节点交直流混合配电网拓扑（假定储能系统配置在2、9、11节点时的情况）

表1 11节点交直流混合配电网负荷与线路参数

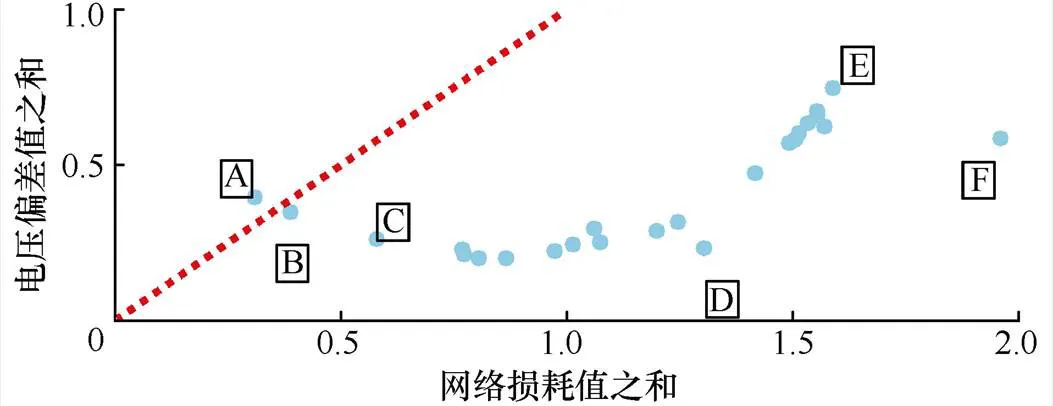
图5 电压偏差之和与网络损耗值之和权重为11时的Pareto最优解集

将图5中代表性强的点进行A～F的标号，计算每个点对应的储能配置的各项数值。图5中代表性特征点解集对比见表2。

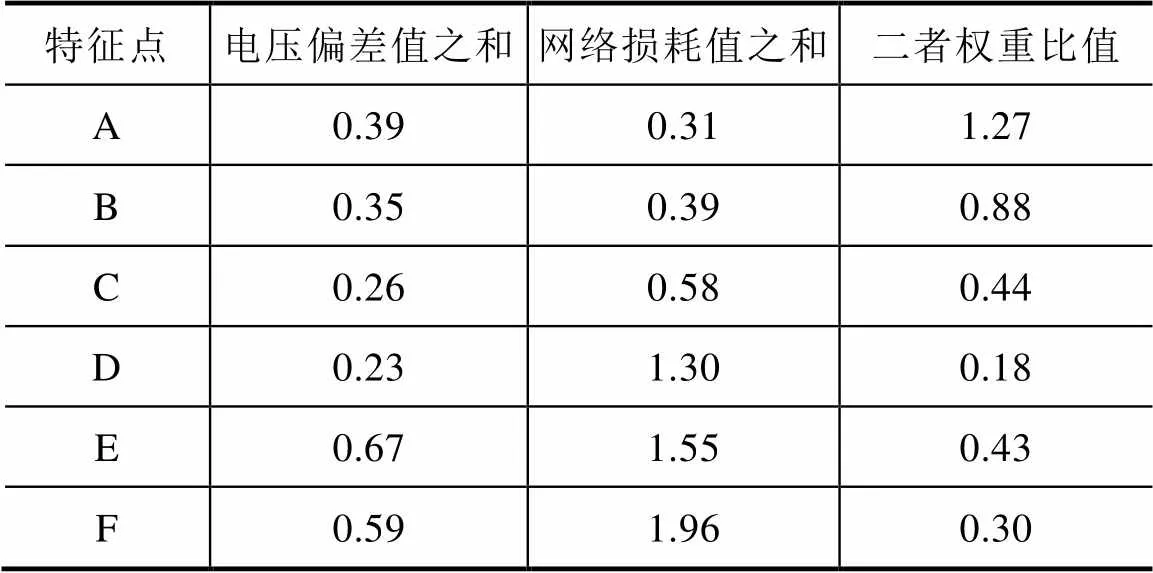
表2 图5中代表性特征点解集对比

为了更好地说明本文所提方法的优越性，将B点的电压偏差值之和与网络损耗值之和数值与其他可行解但非Pareto前沿最优解的某一配置情况及配置储能系统前整个配电网目标函数数值进行对比，分别如图6和图7所示。

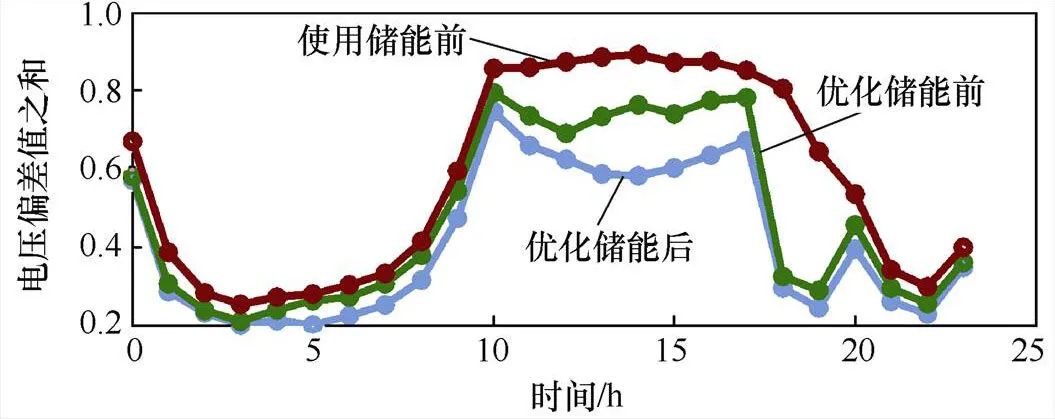
图6 三种情况下的电压偏差值之和对比

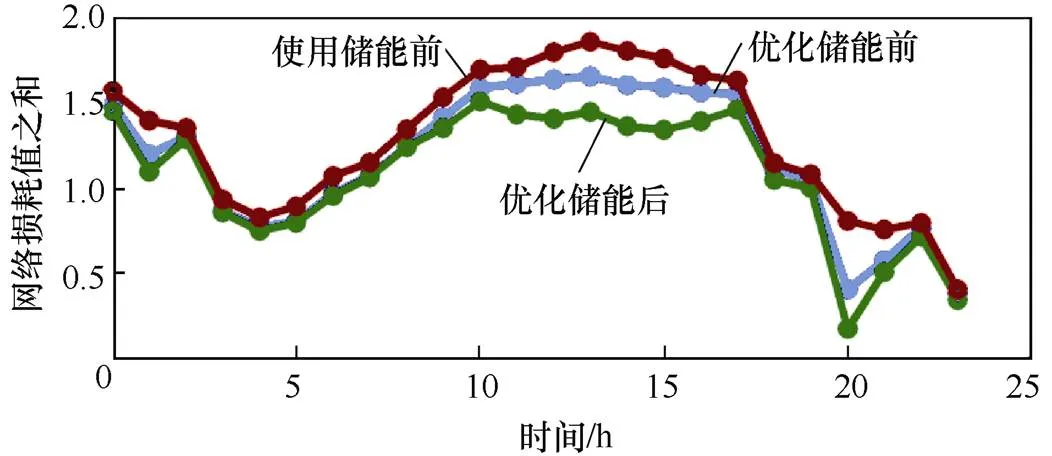
图7 三种情况下的网络损耗值之和对比

从图6与图7可以分析出，将储能系统进行优化配置后，所达到的平抑交直流混合配电网中功率波动的效果要明显优于优化配置，由此证明了本文优化配置方法的有效性。

4 结论

本文重点研究了在交直流混合配电网拓扑中配置同样的储能装置，如何才能达到最好的平抑效果。以时间节点和电气距离意义上的空间节点作为研究切入点，以节点电压偏差值之和及网络损耗值之和两个参数作为评价指标，进行优化储能配置情况的分析与研究。通过优化前后两个指标的对比，验证了本文优化储能配置方法的合理性与可行性。

[1] 杜尔顺, 张宁, 康重庆, 等. 太阳能光热发电并网运行及优化规划研究综述与展望[J]. 中国电机工程学报, 2016, 36(21): 5765-5775.

[2] 陈聪伟, 江修波, 刘丽军. 考虑时序与储能配合的分布式电源优化配置研究[J]. 电气技术, 2017, 18(6): 41-47.

[3] 何頔, 罗进, 唐世虎, 等. 基于非支配排序的改进粒子群算法的含分布式电源的配电网规划[J]. 电气技术, 2018, 19(11): 60-63.

[4] 张健, 王凯悦. 考虑电压稳定性的含分布式电源配电网多目标无功优化[J]. 电气技术, 2020, 21(3): 64-69.

[5] OLIVEIRA T R, SILVA W W A G, DONOSO-GARCIA P F. Distributed secondary level control for energy storage management in DC microgrids[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 2597-2607.

[6] 李鹏程, 张纯江, 袁然然, 等. 改进SOC下垂控制的分布式储能系统负荷电流分配方法[J]. 中国电机工程学报, 2017, 37(13): 3746-3754.

[7] DANESHVAR M, MOHAMMADI-IVATLOO B, ASADI S, et al. Chance-constrained models for transactive energy management of interconnected microgrid clusters[J]. Journal of Cleaner Production, 2020, 271: 122177.

[8] 邓卫, 吴争, 张力, 等. 交直流系统协调控制技术[J]. 高电压技术, 2019, 45(10): 3025-3038.

[9] ESTEFANIA P, JON A, JOSE IGNACIO G, et al. AC and DC technology in microgrid: a review[J]. Rene- wable and Sustainable Energy Reviews, 2015, 43: 726- 749.

[10] 郭玲娟, 魏斌, 韩肖清, 等. 基于集合经验模态分解的交直流混合微电网混合储能容量优化配置[J]. 高电压技术, 2020, 46(6): 527-537.

[11] FARZAM N, LI Y W. Overview of power management strategies of hybrid AC/DC microgrid[J]. IEEE Transa- ctions on Power Electornics, 2015, 30(12): 7072-7089.

[12] 王冉, 王丹, 贾宏杰, 等. 一种平抑微网联络线功率波动的电池及虚拟储能协调控制策略[J]. 中国电机工程学报, 2015, 35(20): 5124-5134.

[13] 汪科, 张雪松, 赵波, 等. 交直流混合微电网网络结构设计和模式切换控制策略[J]. 供用电, 2016, 33(8): 18-22.

[14] 陈安伟. 多母线结构交直流混合微电网协调控制与模式切换策略[J]. 电力系统自动化, 2018, 42(17): 175-186.

[15] 蔡宏达, 夏杨红, 杨鹏程, 等. 交直流混合微电网多模式协调下垂控制[J]. 供用电, 2018, 35(1): 2-7.

[16] WANG Shu, TANG Yuejin, SHI Jing, et al. Design and advanced control strategies of a hybrid energy storage system for the grid integration of wind power generations[J]. IET Renewable Power Generation, 2015, 9(2): 89-98.

[17] 于明, 王毅, 李永刚. 基于预测方法的直流微网混合储能虚拟惯性控制[J]. 电网技术, 2017, 41(5): 1526-1532.

[18] 顾煜炯, 谢典, 和学豪, 等. 海岛直流微网复合储能系统控制策略设计与实现[J]. 电力自动化设备, 2018, 38(6): 1-6.

[19] 朱永强, 张泉, 刘康, 等. 交直流混合微电网分段协调控制策略[J]. 电力系统与自动化, 2020, 44(6): 52-58.

[20] 张海潮, 杨连贺. 基于改进NSGA-Ⅱ的推荐算法[J]. 计算机工程与设计, 2020, 41(9): 2495-2500.

Optimal configuration of energy storage in AC/DC distribution network considering stablilizing voltage fluctuation

GUO Pei

(State Grid He’nan Electric Power Company, Zhengzhou 450000)

In order to solve the problem of power fluctuations caused by the increasing output of volatile new energy sources in the current distribution network, an optimal energy storage configuration method that considers the time and space characteristics of AC/DC hybrid distribution network system power fluctuations is proposed to stabilize the energy storage system. First, a mathematical model for power generation and consumption is established, as well as constraints such as power flow, wind turbines and optical machines, and the alternating iteration method is used to calculate the power flow of the AC/DC hybrid distribution network. Then the model is solved by the fast non-dominated sorting genetic algorithm, and the final output is the comparison chart of the optimization index of the optimal solution and other feasible solutions. Through the optimized configuration of the energy storage system, the deviation value of the distribution network and the network loss are significantly reduced, which verifies the feasibility of the method proposed in the article.

AC/DC distribution network; multi-objective optimization; energy storage system configuration; fluctuation suppression; voltage deviation value sum; network loss

2021-01-29

2021-04-01

郭 沛（1980—），男，硕士，高级工程师，研究方向为配电网规划与设计。