电流互感器铁心剩磁影响因素仿真分析

邓成林 蔡新景 付丁丁

电流互感器铁心剩磁影响因素仿真分析

邓成林 蔡新景 付丁丁

（沈阳工业大学电气工程学院，沈阳 110870）

本文通过Matlab中的Simulink仿真软件对不同影响因素下的电流互感器铁心剩磁进行仿真分析，验证电流互感器铁心剩磁在不同影响因素下的变化规律。研究表明，电流互感器铁心剩磁在暂态非周期分量、故障电流的开断时间、一次回路时间常数、故障短路电流大小及二次负载阻抗值的影响下都有明显的变化；影响因素的作用越强，其产生的剩磁就越大。

电流互感器；剩磁；变化规律；暂态非周期分量；仿真

0 引言

电流互感器对电力系统的测量、保护及计量设备的运行有很重要的作用，其作为电力系统的主要设备之一，是保障整个电力系统安全稳定经济运行的关键设备。电流互感器如果在实际的工作中发生突然断开的现象，铁心就可能出现类似暂态剩磁的情况，从而导致铁心的磁导率降低，致使测量结果与实际数值产生很大的差距，难以到达技术要 求[1-3]。剩磁的存在对于电流互感器的安全稳定运行有很大的影响，尤其是暂态剩磁的影响更大，会导致电流不平衡现象，造成互感器保护误动作[4-5]。

针对电流互感器铁心剩磁的问题，研究人员做了大量研究并取得一定进展。梁仕斌等通过对电流互感器进行充磁、退磁试验得出了剩磁对电流互感器的影响[6]。文峰和谭宁介绍了电流互感器产生剩磁的原因，并基于剩磁产生机理研究了剩磁对电流互感器稳态、暂态性能的影响[7]。周迁从原理上分析电流互感器误差和剩磁产生的原因，针对运行过程中的电流互感器，结合现场工作经验，归纳产生剩磁的因素，阐述剩磁对电流互感器误差的影响，并提出了减少剩磁的措施[8]。但这些研究都没有从剩磁的产生机理出发分析影响剩磁的因素和对影响因素下的剩磁进行定量的分析。崔迎宾等应用电磁暂态仿真程序ATP对电流互感器暂态剩磁产生的原因及不同因素对剩磁的影响进行了系统的计算分 析[9]。可见，通过计算机仿真软件对电流互感器铁心剩磁的影响因素进行仿真分析得出其变化规律是至关重要的，这为以后对电流互感器铁心的剩磁抑制提供了理论基础。

本文采用Matlab中的Simulink仿真软件对电流互感器铁心剩磁的影响因素进行仿真分析，通过仿真软件搭建电流互感器的仿真模型，绘制具体的励磁曲线并选取合适的参数，对不同影响因素下铁心剩磁的大小进行定量分析。

1 电流互感器铁心剩磁影响因素分析

1.1 电流互感器一次侧故障时短路电流分析

电流互感器一次侧故障时的简化电路如图1所示。电路中串联的电感和电阻可以等效电流互感器的一次侧。互感器一次侧的电源是一个交流电压源m，其数值等于sin(+)。在此通过控制交流电压源的相位来模拟电流互感器运行的稳态与暂态状态，电路中会产生稳态与暂态的短路电流。

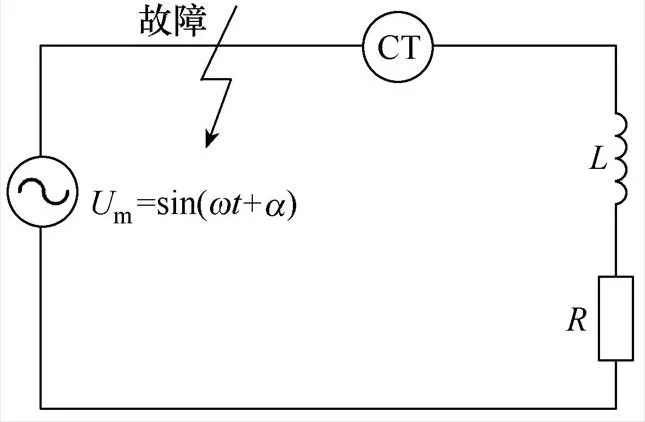
图1 电流互感器一次侧故障时的简化电路

设故障在0时发生，则此时的电路方程为

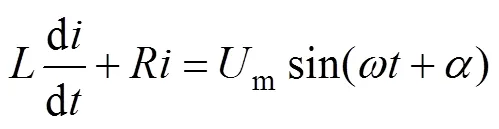
其通解为

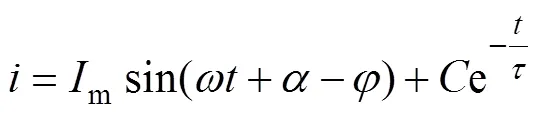
式中：m为一次侧故障短路电流周期分量幅值；为短路故障后功率因数角；为一次时间常数；为积分常数；为电流电压初相位[10]。

由于电路中的电感电流不能突变，则短路前后电流瞬时值相等[11]，常数为

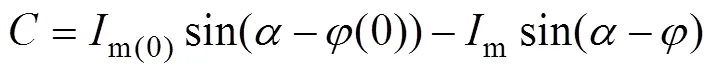
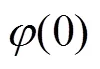
由于故障前负荷电流较小，故设m(0)=0，则短路电流公式可以简化为

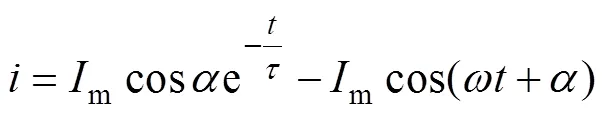
由式（4）可知，故障短路电流由两部分组成：稳态短路电流与暂态短路电流。当=90°时，非周期分量很小接近于零，电流互感器处于稳定运行状态。当=0°时，非周期分量达到最大值，铁心中的磁通快速增加直到饱和。当暂态短路电流中时间常数不变时，非周期分量会随时间逐渐减小，铁心中的磁通增加量也逐渐减小直到饱和。

1.2 影响剩磁的因素

电流互感器铁心中剩磁的大小主要由电流互感器一次侧开断瞬间铁心中的磁通决定。铁心中的磁通与暂态非周期分量、故障短路电流的大小、二次负载的阻抗值相关[12]。暂态非周期分量的大小还与故障短路电流开断时间和一次回路时间常数有关。

综上所述，剩磁的影响因素主要有：

1）暂态非周期分量

由式（4）分析可知，非周期分量越大，暂态短路电流就越大，铁心中磁通增加的速率就越快，铁心中的磁通就越多，则剩磁就越多。

2）故障短路电流开断时间

3）一次回路时间常数

4）故障短路电流大小

从上文可知一次故障短路电流是由稳态分量与暂态分量构成。由式（4）可知，它的大小主要由m和cos决定。一次短路电流越大，mcos就越大，非周期分量就越大，则剩磁就越多。

5）二次负载的阻抗值

电流互感器铁心中的磁通与电流互感器二次侧回路的阻抗值有直接的关系。如果二次侧接的是纯电感，电流互感器铁心中几乎不存在剩磁。若电流互感器二次侧接的是纯电阻，电流互感器就会存在很大的剩磁[10]。在电流互感器正常运行中，为避免大量剩磁应选二次负载阻抗小的电流互感器。

2 电流互感器仿真模型分析

在Simulink仿真软件中可以选用饱和变压器元件来作电流互感器仿真模型。根据文献[13]的公式可以计算饱和变压器中的参数：绕组阻抗2、2和励磁阻抗m。电流互感器铁心剩磁影响因素仿真模型如图2所示。

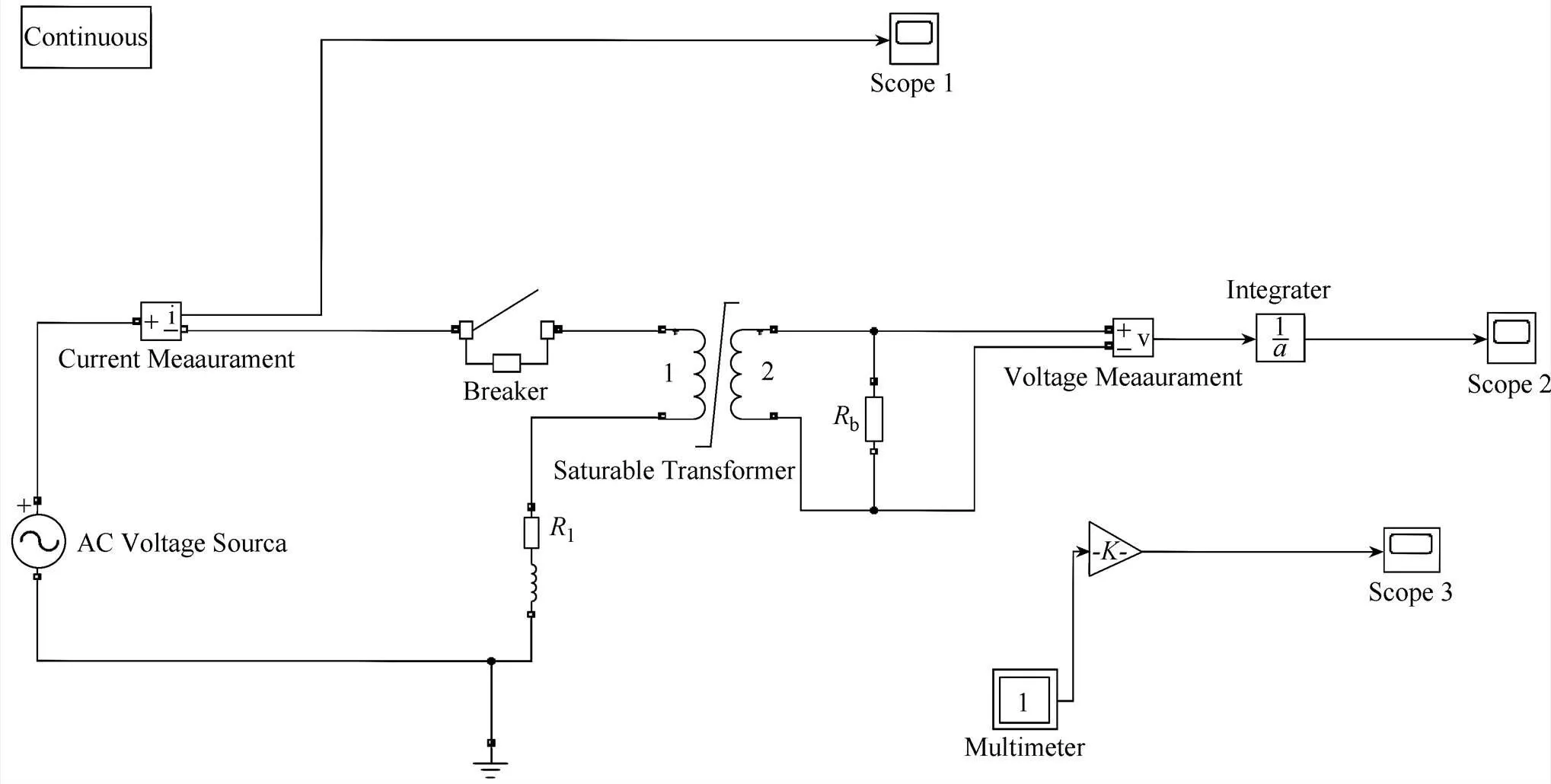
图2 电流互感器铁心剩磁影响因素仿真模型

电流互感器参数设定：匝数比=1/200，电流比=1 000A/5A，额定容量b=50kA，二次负载b=1W。

本文根据铁心磁化曲线和饱和磁通的定义计算出饱和点（0.1, 2）（标幺值）。通过Powergui中的Hysrersis Design软件画出所需的励磁曲线如图3 所示。

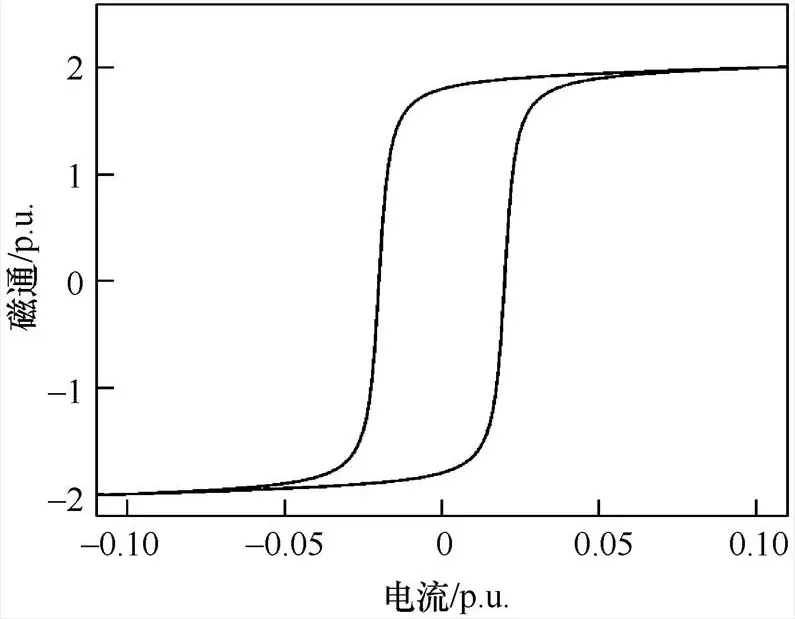
图3 励磁曲线

电流互感器铁心中的磁通是通过万用表来测量的，为标幺值（p.u.）。通过设置断路器开断时间模拟故障电流的开断时间。在仿真中，当断路器断开时，铁心中的瞬时磁通就是剩磁[14]。

3 剩磁影响因素的计算分析

在仿真中，假设电流互感器铁心中没有初始剩磁。快速保护装置要求在短路故障发生后2～3个周期内动作，因此设置仿真时间为0.08s。

3.1 暂态非周期分量

设m=1.2kA，0.06s，二次负载b=1W，=0.06s时断路器断开，非周期分量与剩磁之间的关系如图4所示。

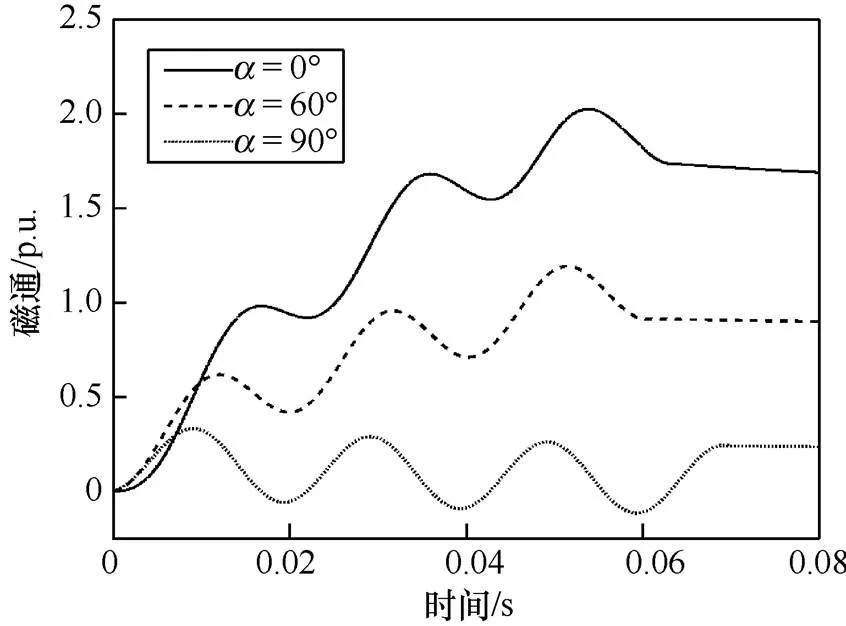
图4 非周期分量与剩磁之间的关系

图4给出了=90°（非周期分量最小）、= 60°和=0°（非周期分量最大）时，铁心磁通的变化曲线，可以看出，在前期，=0°时铁心中磁通的增长速度比=60°和=90°时的要快，随着时间的增加，磁通逐渐累积，这是励磁电流中非周期分量作用的结果。在=0°、=0.055s时，铁心中磁通饱和。在=0.06s断开时，可以看出=90°的磁通在这一时刻并没有停止变化，这是由于系统故障时，短路电流在过零点时，断路器才会动作，电路才会断开。在断路器断开后，铁心中磁通会从这一刻开始逐渐减弱，这个过程称为动态剩磁。

由前面分析可知，剩磁的大小与断路器开断时铁心中的瞬时磁通量相同，从图4可以看出非周期量越大，剩磁越大。

3.2 故障短路电流开断时间

设m=1.2kA，0.06s，二次负载b=1W，= 0°，短路电流的开断时间为仿真时间0.08s。将以上参数代入仿真模型，故障短路电流开断时间与剩磁之间的关系如图5所示。

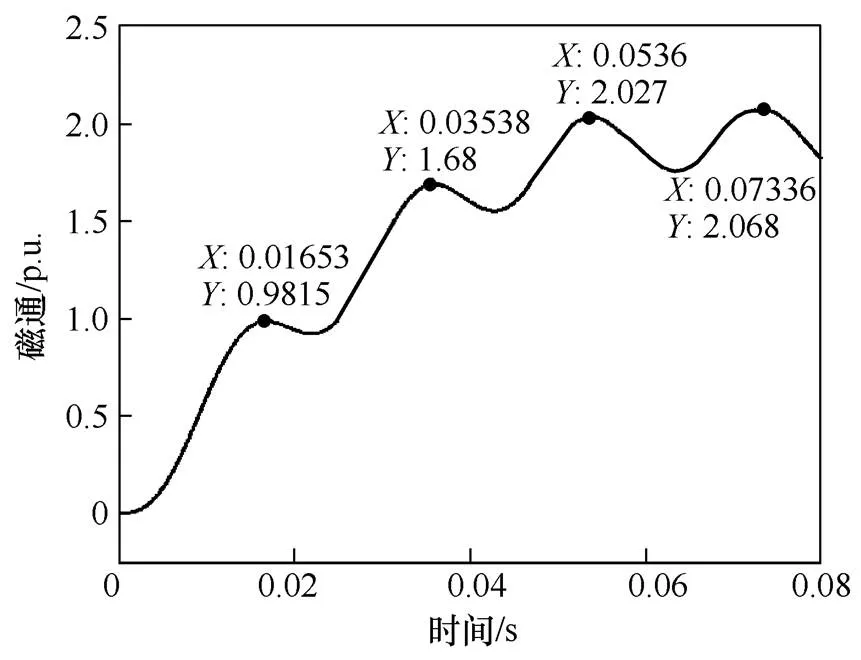
图5 故障短路电流开断时间与剩磁之间的关系

由图5可知，图中曲线上有4个点，每个点代表断路器开断时间为0.01s、0.03s、0.05s和0.07s时铁心中瞬时磁通。从图5可以看出，每个点的磁通量要比断路器开断瞬间的磁通量大，这是由于短路电流过零点时断路器才能开断，断路器断开的瞬间，短路电流尚不为零，磁通仍在不断累积。相邻两点之间有一段磁通值是下降的，这是励磁电流非周期分量负向去磁作用大的结果。

总体上看，剩磁随故障电流开断时间增加而增大。若要电流互感器发生故障时铁心中的剩磁小，就要减小短路电流的开断时间。电流互感器的一次侧应采用快速动作的继电保护装置，缩短自动重合闸的时间。

3.3 故障短路电流的大小

设0.06s，二次负载b=1W，=0.06s时断路器断开，故障短路电流分别取1 200A、1 000A、800A。在=90°和=0°两种情况下分析不同短路电流与剩磁的关系分别如图6和图7所示。

由图6和图7可以看出，在其他条件不变的情况下，不管非周期分量是最大或最小，增大故障短路电流，铁心中的剩磁随之增加。当非周期分量最大时（=0°）时，可以看出剩磁随着一次短路电流的增加而增加直至饱和。非周期分量最小（=90°）时剩磁随一次短路电流增加而增加，但增加的很小，这是由于非周期分量快接近于零，电流互感器在稳定运行，铁心中产生的是稳定剩磁。尽管一次短路电流增加很大，但剩磁增加很少，基本不会变化。

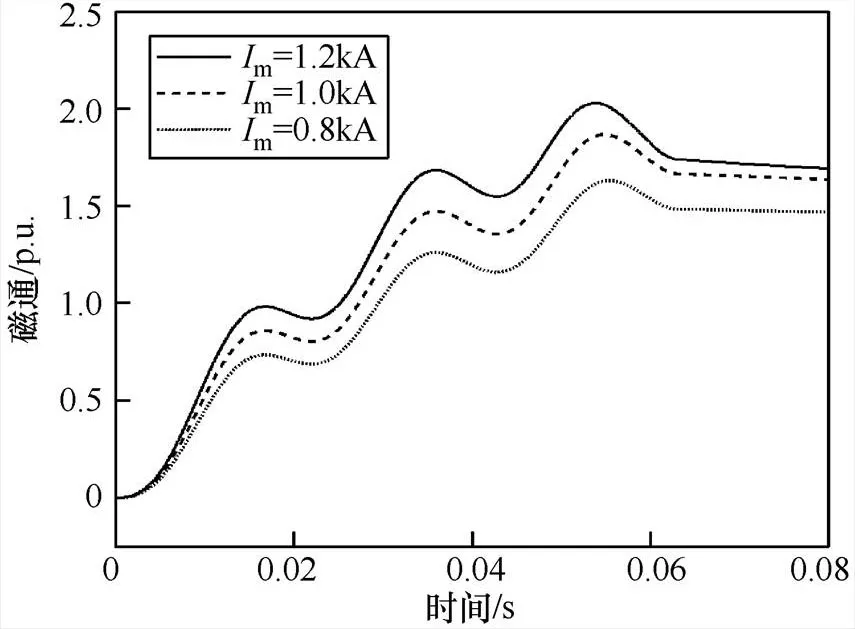
图6 a=0°时不同短路电流与剩磁之间的关系

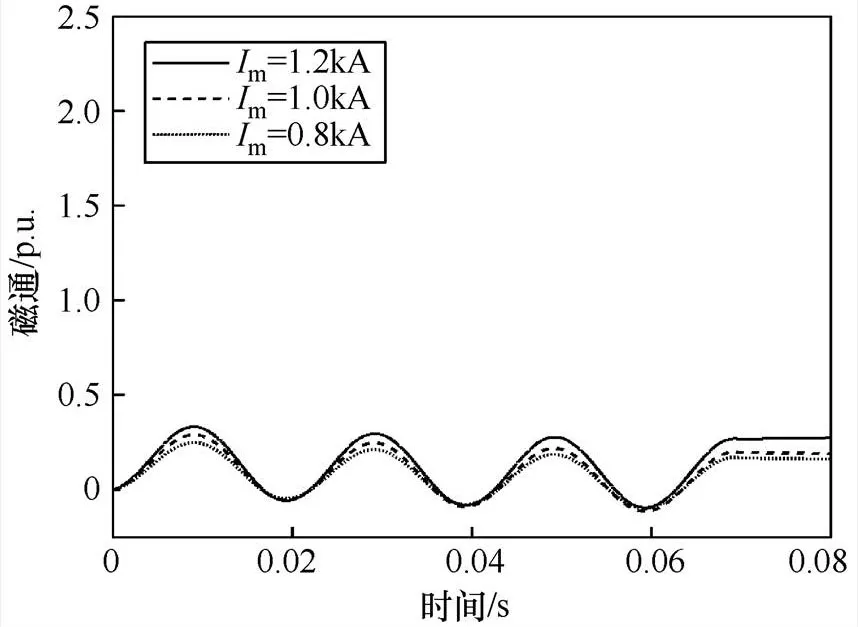
图7 a=90°时不同短路电流与剩磁之间的关系

3.4 一次回路时间常数

设=0°，m=1.3kA，二次负载b=1W，=0.06s时路器断开，将以上参数代入仿真模型，一次回路时间常数与剩磁之间的关系如图8所示。

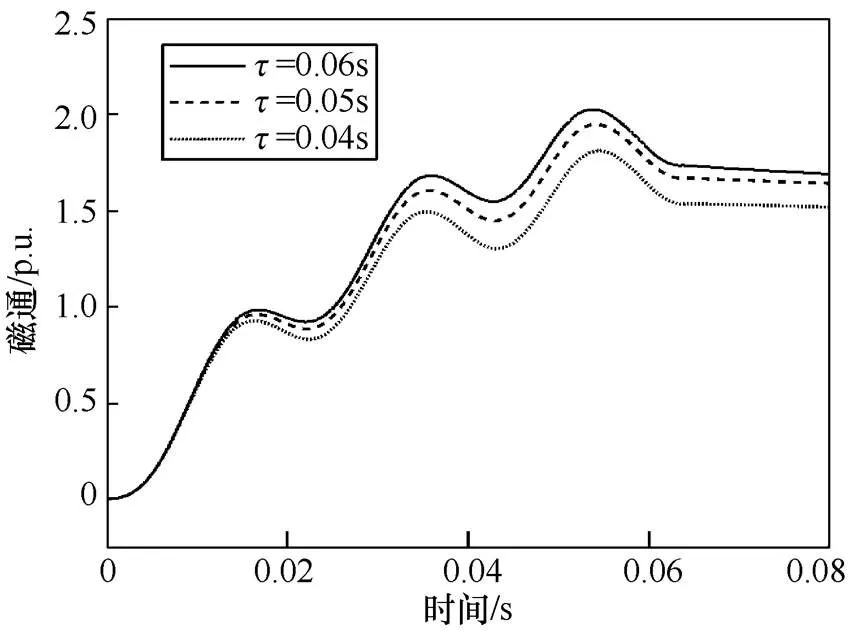
图8 一次回路时间常数与剩磁之间的关系

由图8可知，一次时间常数越大，剩磁越大。一次时间常数与非周期分量增长的速率相关，一次时间常数越大，非周期分量增长越快，铁心中的磁通积累越多，导致铁心中产生大量剩磁。

3.5 二次负载的阻抗值

设=0°，m=1.2kA，0.06s，二次负载b分别为1W、0.8W和0.6W，=0.06s时断路器断开。二次负载与剩磁的关系如图9所示。

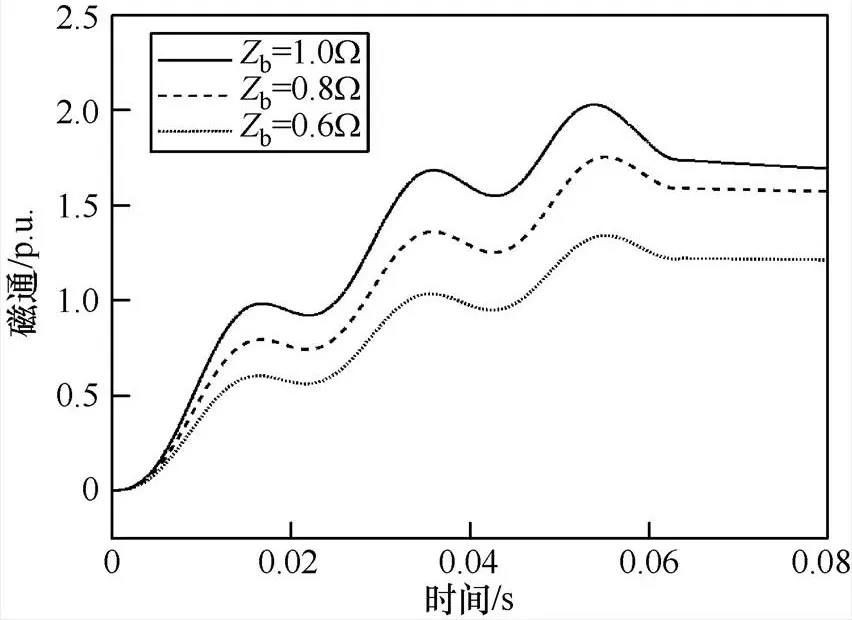
图9 二次负载与剩磁之间的关系

由图9可知，在其他条件不变的情况下，在=0.06s时断开，剩磁随着二次负载的增大而增大。当二次负载b=1W时，=0.06s铁心磁通饱和。在电流互感器正常运行中，为避免大量剩磁应选二次负载阻抗小的电流互感器。

4 结论

本文采用计算机仿真软件Matlab中的Simulink对电流互感器铁心剩磁的影响因素进行了仿真分析。电流互感器铁心中剩磁在暂态非周期分量、故障电流的开断时间、一次回路时间常数、故障短路电流大小及二次负载的阻抗值等不同因素影响下都有其变化规律。在以上影响因素的作用下，影响因素作用越强，产生的剩磁就越大。分析得知暂态非周期分量越大，剩磁越大；故障电流的开断时间越长，剩磁越大；一次回路时间常数越大，剩磁越大；故障短路电流越大，剩磁越大；二次回路阻抗值越大，剩磁越大。

[1] 何东莹, 李海荣, 左黎斌, 等. 计量用电流互感器剩磁产生的原因及影响分析[J]. 云南电力技术, 2019, 47(4): 47-49.

[2] 苏贤, 项宇锴. 不同负载特性下的全工况电流互感器仿真研究[J]. 电气技术, 2021, 22(2): 48-53, 77.

[3] 刘涛, 刘鑫, 梁仕斌, 等. 基于极性变化直流电压源的铁磁元件铁心剩磁通测量方法[J]. 电工技术学报, 2017, 32(13): 137-144.

[4] 马鸿波, 刘鑫, 刘涛. 铁磁元件直流退磁方法研究[J]. 云南电力技术, 2019, 47(3): 57-61, 64.

[5] 段进宽, 郭磊. 电流互感器回路直流分量对差动保护特性影响的实例分析[J]. 电气技术, 2020, 21(1): 89-92.

[6] 梁仕斌, 文华, 曹敏, 等. 铁心剩磁对电流互感器性能的影响[J]. 继电器, 2007(22): 27-32.

[7] 文峰, 谭宁. 实际剩磁对电流互感器性能的影响[J].贵州电力技术, 2013, 16(2): 67-69.

[8] 周迁. 剩磁对电流互感器误差的影响[J]. 通信电源技术, 2018, 35(12): 32-33.

[9] 崔迎宾, 谭振宇, 李庆民, 等. 电流互感器剩磁影响因素和发生规律的仿真分析[J]. 电力系统自动化, 2010, 34(23): 87-91.

[10] 袁兆强, 凌艳. 基于MATLAB的电流互感器饱和特性仿真分析[J]. 湖北电力, 2007(3): 24-26.

[11] 王学超, 王士伟, 姚亮. 电流互感器饱和的原因浅析[J]. 东北电力技术, 2015, 36(5): 36-40.

[12] 杨婉霞, 王关平, 孙伟, 等. 基于Simulink的电流互感器建模与性能检测仿真实验教学设计[J]. 中国农机化学报, 2019, 40(1): 117-121, 173.

[13] 袁季修, 盛和乐, 吴聚业. 保护用电流互感器应用指南[M]. 北京: 中国电力出版社, 2003.

[14] 肖伟平, 黄绍平. 基于MATLAB的电流互感器饱和特性仿真分析[J]. 变压器, 2005(5): 27-30.

Simulation analysis of factors affecting remanence of current transformer core

DENG Chenglin CAI Xinjing FU Dingding

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870)

In this paper, Simulink software in Matlab is used to simulate and analyze the remanence of current transformer core under different influence factors and verify that the remanence of current transformer core has its changing law under different influence factors. The results show that the remanence in the current transformer core changes obviously under the influence of the transient aperiodic component, the breaking time of the fault current, the time constant of the primary circuit, the amplitude of the fault short circuit current and the impedance of the secondary load. The stronger the influence factors, the greater the remanence will be.

current transformer; remanence; variation law; transient aperiodic component; simu- lation

2021-01-19

2021-03-21

邓成林（1995—），男，辽宁辽阳人，硕士研究生，主要研究方向为高压电器。