位姿偏差对X-Y井径测井仪测量精度的影响分析

路艳齐，郭振华，焦利明

(中国电子科技集团公司第二十二研究所 河南 新乡 453003)

0 引 言

井径测量是一种测量油井井眼几何形态的测井方法，井径曲线也是石油标准测井的必测曲线。在测量过程中发现，井径测量值与真实值经常会出现一定误差。龚子华等[1]主要从井径推靠部分设计原理、机械传动间隙、电位器精度等方面分析了井径测量误差，并未考虑仪器轴线与井眼轴线存在的位姿偏差的影响；张道奎[2]主要从井径仪机械结构、电子线路和测量原理等方面对测量误差进行了分析，同样未考虑位姿偏差的影响；吴兴方等[3]考虑了井径仪居中程度，即位移偏差对三臂井径仪测量误差的影响，但并未考虑姿态偏差的影响。

引起井径误差的原因有多种：一种是井径测井仪本身精度不足带来的误差，包含仪器推靠部分的设计误差以及加工、装配误差，采集传感器误差、以及长期使用带来的磨损误差等；一种是测量原理的误差，某些井径测量模型假设测量过程中仪器完全居中，还有一些测量模型则假设仪器轴线与井眼轴线完全重合，这些假设显然是存在一定误差的。

为研究位姿偏差对X-Y井径仪测量精度的影响，改善井径测量精度，本文将建立3个井径数学模型(均不考虑其他因素对井径测量的影响)，并通过分析、计算不同模型的误差值及应用条件，择优选取适合工程应用的井径模型。

1 井径模型

模型一：假设仪器在油井内完全居中，即不考虑位姿偏差的影响。

模型二：假设仪器在油井内只有位移偏差，即不考虑姿态偏差的影响。

模型三：仪器在油井中为任意位移和姿态，即同时考虑位姿偏差的影响。

对于模型一与模型二，本文采用平面几何图形分析法建立数学模型进行分析。对于模型三，本文建立空间直角坐标系，采用空间直角坐标变换的方法，建立数学模型进行分析。

1.1 模型一

仪器在油井横截面上的俯视图如图1所示。其中，O为井眼中心，P为仪器中心，O、P重合。A、B、C、D分别为仪器测量臂与油井内壁的接触点。PA、PB、PC、PD分别是仪器4条测量臂在油井横截面上的投影，其长度分别为井眼半径的测量值。

图1 仪器居中时在油井横截面上的俯视图

此模型下，最终的井径测量直径d为仪器4条测量臂测量直径的平均值，即

(1)

1.2 模型二

仪器轴线与井眼轴线平行但不重合，仪器在油井横截面上的俯视图如图2所示。

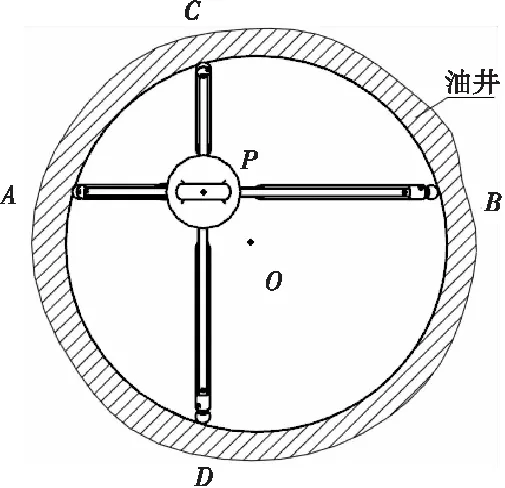
图2 仪器存在位置偏差时在油井横截面上的俯视图

P为仪器中心，O为井眼中心。其几何分析示意图如图3所示，其中PA、PB共线，PC、PD共线，且PA、PB分别与PC、PD垂直。

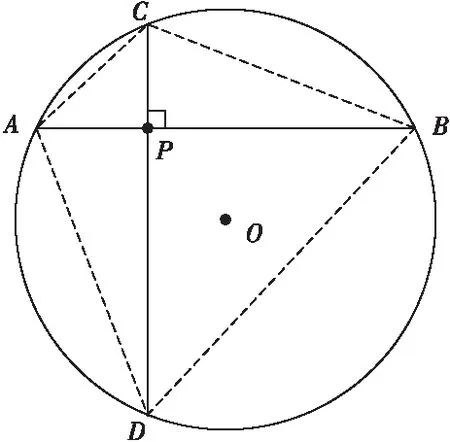
图3 仪器存在位置偏差时的几何分析示意图

由于A、B、C、D都位于油井内壁上，由正弦定理：

(2)

式中：R为井眼半径，mm。

则此模型下，最终的井径测量直径d为:

(3)

其中，根据直角三角形性质：

(4)

(5)

(6)

1.3 模型三

仪器轴线与井眼轴线为任意位姿关系，仪器在油井横截面上的俯视图如图4所示。

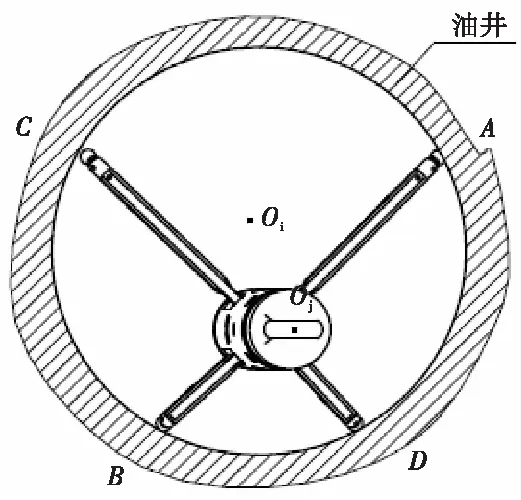
图4 仪器存在位姿偏差时仪器在油井横截面上的俯视图

采用空间直角坐标系，建立仪器坐标系Oj-XjYjZj，坐标系原点Oj在仪器轴线上，Z轴沿仪器轴线，其正方向为沿仪器下接头到上接头的方向；OjA沿X轴正方向，OjB沿X轴负方向，OjC沿Y轴正方向，OjD沿Y轴负方向。

在仪器坐标系中，测量臂与油井内壁的接触点的坐标分别为A(Axj，0，Azj)，C(0，Cyj，Czj)，B(Bxj，0，Bzj)，D(0，Dyj，Dzj)。其中，Axj，Cyj，Bxj，Dyj分别为仪器测量臂的测量值。

采用空间直角坐标系，建立参考坐标系Oi-XiYiZi，坐标系原点Oi在井眼轴线上，Z轴沿井眼轴线，其正方向为沿井眼轴线由下到上。设仪器坐标系Oj-XjYjZj由参考坐标系经过下列变换生成[4-5]：1)绕Xi轴旋转α度；2)绕Yi轴旋转β度；3)沿Xi轴平移Δx；4)沿Yi轴平移Δy。

设空间上的一点在仪器坐标系中的坐标为(xj，yj，zj)，在参考坐标系中的对应坐标为(xi，yi，zi)。则由坐标变换可知：

(8)

其中：

Tij(α,β,Δx,Δy)=Trans(yi,Δy)×Trans(xi,Δx)
×Rot(yi,β)×Rot(xi,α)

(9)

(10)

(11)

(12)

(13)

在参考坐标系中，仪器测量臂与油井内壁接触点的对应坐标分别为A(Axi，Ayi，Azi)，C(Cxi，Cyi，Czi)，B(Bxi，Byi，Bzi)，D(Dxi，Dyi，Dzi)。

(14)

(15)

(16)

(17)

在参考坐标系中，A、C、B、D均在方程为x2+y2=R2的圆柱面上，其中R为井眼半径，则：

Axi2+Ayi2=RA2

(18)

Cxi2+Cyi2=RC2

(19)

Bxi2+Byi2=RB2

(20)

Dxi2+Dyi2=RD2

(21)

式中：RA，RB，RC，RD分别为测得的井眼半径，mm。

联立方程(8)～(21)，可分别求得RA，RB，RC，RD。此模型下最终的的井径测量直径d为：

(22)

1.4 特殊情况下的井径值判定

若仪器的4条测量臂在同一时刻均与井壁接触，则如上文所述，井径值为4条测量臂测量直径的平均值。

当井眼直径较大或者仪器偏心量较大时，可能导致1条或多条测量臂不能可靠地接触井壁[6]。若只有1条测量臂接触不到井壁，可按上文所述，井径值由其余3条测量臂确定。若有2条以上测量臂接触不到井壁，则测量无效，此时应及时判断问题并找出原因。

2 模型误差验算

采用模型三获取井眼测量直径时，必须已知仪器的位姿偏差值。但模型三不存在原理性误差，故下文将其作为基准，分析验算其他两种模型的误差。

假设已知仪器轴线与井眼轴线的位姿偏差，同时知道井眼直径。将已知条件带入模型三，可以反求出仪器4条测量臂测量值。将得到的测量值分别代入模型一、模型二，求得相应的直径后，与已知直径比较，即可求得模型一和模型二的误差。

以中国电子科技集团公司第二十二研究所独立研发设计的SDZ-5120四臂井径微球微电极短节为例，分析2种模型的误差。SDZ-5120的主体直径为100 mm，有效长度为2 735 mm。设待测井眼直径为300 mm，该仪器在进行井径测量时，最大姿态偏差角不大于4°，最大位置偏差量不超过40 mm。故α、β按-4°、-2°、0°、2°、4°各取5组，Δx,Δy按-40、-20、0、20、40 mm各取5组。

对于4个输入变量α,β,Δx,Δy，若按全因素全水平进行试验，需要进行625次。为减小试验次数，同时保证试验的有效性，按照正交试验法来设计试验，如表1所示。绘制模型一和模型二的测量井径误差图，如图5所示。

表1 不同位姿偏差下模型一和模型二的测量井径

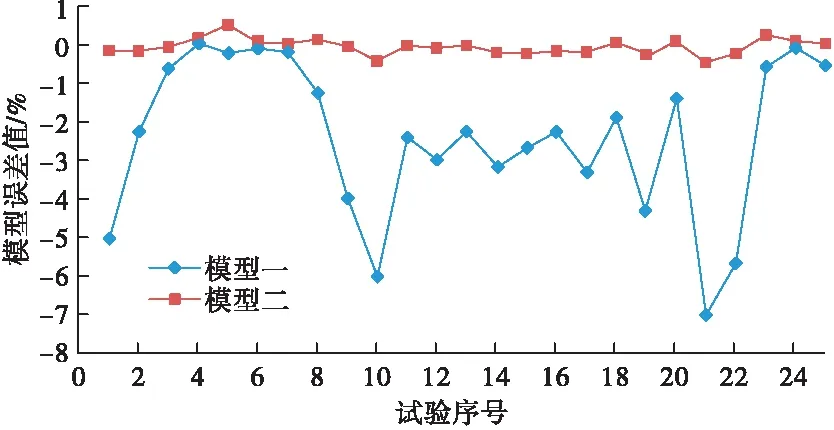
图5 不同位姿偏差下模型一和模型二测量误差曲线

由图5可知，模型一的误差均为负偏差，最大测量偏差为-7.03%，平均偏差为-2.39%；由于考虑了位移偏差的影响，模型二误差值较小，最大偏差值为-0.45%。

3 结 论

本文通过建立3个井径数学模型，研究、分析了位姿偏差对X-Y井径仪井径测量的影响。之后，通过不包含原理性误差的模型三，定量分析验算了模型一和模型二的误差。验算结果表明，由于考虑了位移偏差的影响，模型二的误差要小于模型一的误差。

模型三虽然不存在原理性误差，但应用此模型进行井径测量时，需已知仪器在井眼中的位姿偏差，而位姿偏差一般难以获得。采用模型二进行井径测量时不需要额外的输入参数，且测量误差小，能够满足工程应用的要求，故建议将模型二作为井径测量模型。