基于双参数模型的地铁车站地震易损性分析

姜京伟，李静波，崔春义，许民泽，苏 健，张 鹏

1)山西省交通科学研究院，山西太原030006；2)大连海事大学土木工程系，辽宁大连116026； 3)大连海洋大学海洋与土木工程学院，辽宁大连116023

近年来，随着地下工程大面积建设，地铁工程等地下结构已经成为城市生命线的重要组成部分，而中国是一个地震多发国家，一旦发生地下结构破坏可能造成巨大经济损失[1-3]．因此，开展地铁车站结构的地震易损性研究，对地下结构防灾减灾具有重要意义和指导作用．

在结构地震易损性分析方面，许多学者已开展了大量研究．BAKHSHI等[4]针对地面动峰值加速度及结构整体延性能力对结构地震破坏规律进行了分析．AMIN等[5]通过静力推覆分析，建立了储罐地震易损性曲线．PANG等[6]充分考虑了地震动及结构的不确定性，采用云图法开展了斜拉桥地震易损性分析．SCHWARZ等[7]针对框架结构填充墙的影响，利用土耳其地区的震害数据，得到了框架结构地震动参数与超越概率易损性模型．江辉等[8]基于增量动力分析方法研究了深水环境下连续刚构桥的地震损伤特性．苏亮等[9]采用机器学习手段，提出了针对钢筋混凝土(reinforced concrete, RC)框架结构地震易损性的快速分析方法．何浩祥等[10]以弹塑性耗能差为损伤指标，建立了单体建筑结构及区域建筑群损伤-恢复全过程函数模型．蒋亦庞等[11]研究了结构参数不确定性对无筋砌体结构地震易损性的影响．胡思聪等[12]围绕氯离子扩散及钢筋锈蚀机理，研究了近海桥梁的时变地震易损性．张永群等[13]基于蒙特卡洛模拟的方法，对多层砌体结构地震易损性进行了讨论. KOUTSOURELAKIS等[14]结合马尔科夫链算法，提出了基于贝叶斯方法的易损性理论分析框架．KIANI等[15]考虑断层对隧道的影响，基于离心实验提出了冲积层中的隧道易损性分析方法．钟紫蓝等[16]采用增量动力分析方法，以层间位移角为损伤参数探讨了不同地震动强度指标对两层三跨地铁车站地震损伤的影响规律．黄忠凯等[17-18]充分虑地震动及土层参数不确定性，开展了软土地区隧道结构地震易损性分析．ARGYROUDIS等[19]从衬砌钢筋腐蚀退化效应出发，考虑土-结构相互作用的影响，提出了浅埋地铁隧道地震易损性曲线的数值计算方法．

以上地震易损性研究多采用单一指标变量，未深入考虑多因素的耦合关联性．而震害调查与实验结果表明，结构地震损伤是由大位移幅值和循环加载效应的联合作用所导致[20]，结构累积损伤和结构最大反应的破坏界限存在耦联关系．因此，本研究采用可同时考虑变形与能量的双参数损伤模型，进行饱和砂土场地中地铁车站结构地震易损性分析．

1 数值模型的建立

基于开源化计算平台OpenSees，以某单层双跨地铁车站为研究对象，建立饱和砂土场地-地铁车站非线性动力体系数值模型，如图1和图2．场地尺寸170 m×30 m，结构埋深6 m，土体材料选用修正多屈服面塑性本构模型，密度为1 900 kg/m3、内摩擦角为33°、泊松比为0.35，剪切波速为200 m/s.为考虑钢筋混凝土非线性变形，结构采用纤维截面梁单元[21]，混凝土和钢筋分别选用Concrete02材料和Steel02材料，本构模型见图3．其中，图3中各变量含义请扫描文末右下角二维码．

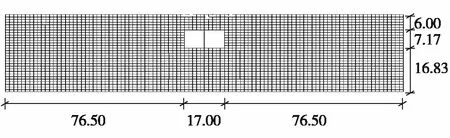
图1 数值模型(单位：m)Fig.1 (Color online) Numerical model(unit：m)

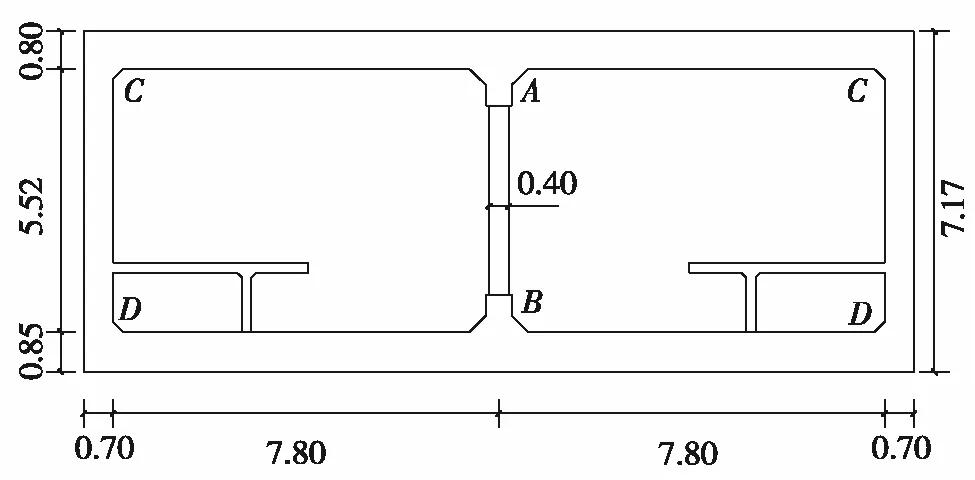
图2 地铁车站结构横截面示意图(单位：m)Fig.2 Cross-sectional schematic of subway station structure(unit：m)

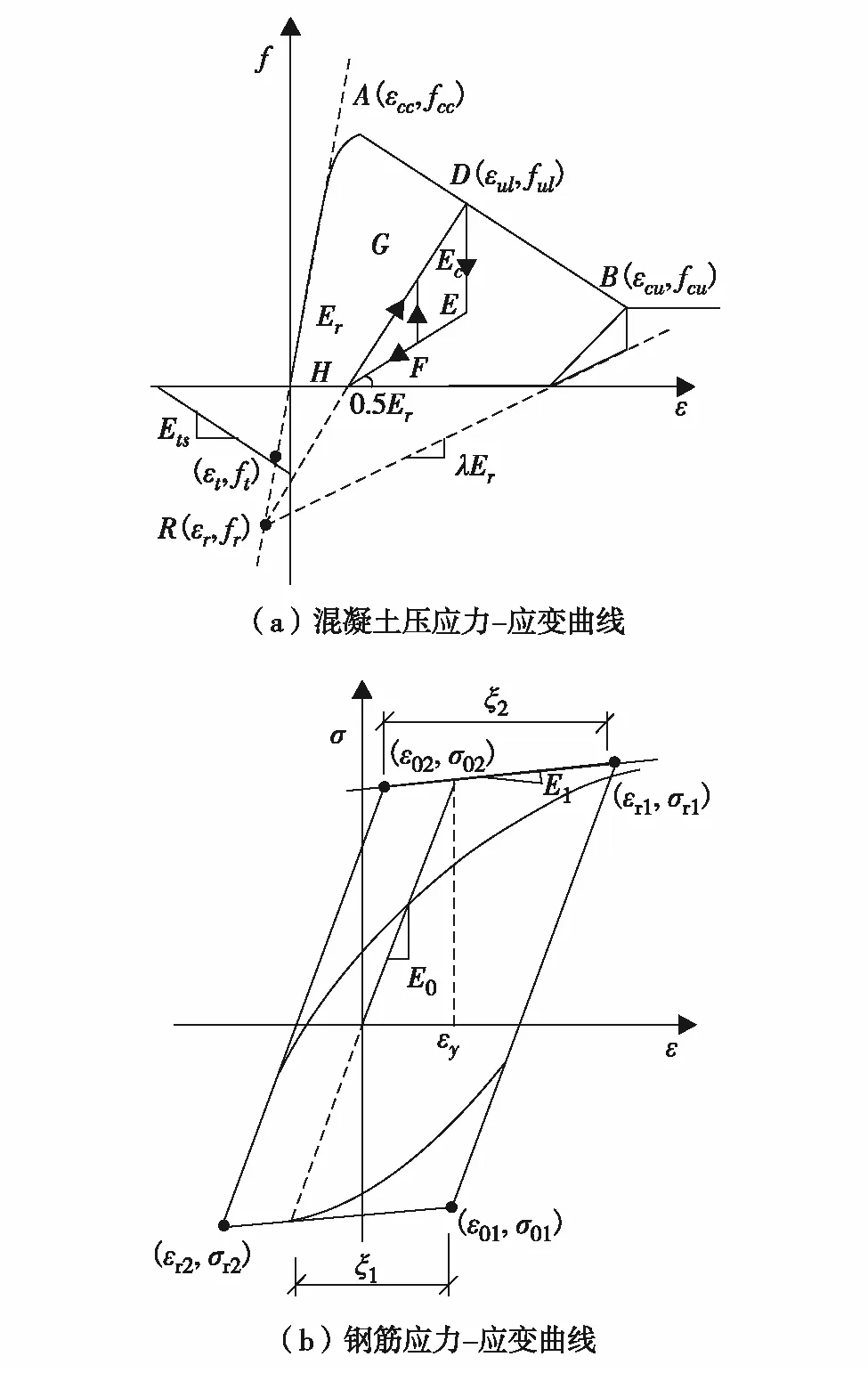
图3 钢筋和混凝土的本构模型Fig.3 Constitutive models for concrete and reinforcement

已有研究表明，合理选取20条地震动作为输入，可有效反映地震记录的不确定性影响[22]．本研究考虑场地类别和地震动强度等条件，从PEER数据库中选取20条地震波，时程曲线如图4．其中，g为重力加速度．

图4 地震波时程曲线Fig.4 (Color online) Time-history of seismic waves

2 损伤模型与量化指标选取

2.1 双参数损伤模型

双参数损伤模型可同时考虑结构变形与能量损耗，因而较单参数模型更具有理论优越性[23]．牛荻涛等[24]基于三线性刚度退化模型(图5)，提出了改进的双参数地震破坏模型．其中，xy和xu分别为屈服位移和极限位移；fy和fu分别为发生屈服位移和极限位移时所受的力；k0和k1分别为初始刚度和屈服刚度．通过实际震害资料及结构数据，将最大变形与滞回耗能非线性组合，有

D=xm/xu+0.138 7(ε/εu)0.081 4

(1)

其中，D为结构损伤指数；xm为构件在地震作用下最大弹塑性变形；xu为构件极限变形；ε为构件在地震作用下累计滞回耗能；εu为构件极限耗能．

图5 三线性刚度退化模型[24]Fig.5 Trilinear stiffness degradation model curve[24]

2.2 结构损伤量化指标选取

根据已有地下结构及钢筋混凝土框架的地震易损性研究资料[16,25]，将地铁车站结构性能划分为正常使用(PL1)、立即使用(PL2)、生命安全(PL3)、防止坍塌(PL4)4个水准，并分别与结构损伤状态相对应. 当D≤PL1时，定义结构损伤状态为基本完好；PL1PL4时，定义结构损伤状态为倒塌.

为考虑土-结构相互作用的影响，对结构进行静力推覆分析[26]，得到中柱底部弯矩-转角曲线．根据钱嫁茹等[27]提出的RC柱四折线弯矩-转角骨架线，确定地铁车站结构的极限状态限值，四折线弯矩-转角骨架线及其性能点示意图如图6．其中，B点为名义屈服点，对应中柱屈服弯矩My和屈服转角θy；C点为峰值点，对应中柱的峰值弯矩Mp和峰值转角θp；F点为极限点，对应极限弯矩Mu和极限转角θu；E点为结构失效点，对应极限弯矩Mr和θr．

图6 RC柱四折线M-θ骨架线及性能点示意图Fig.6 Four-linear M-θ skeleton curve and performance points for RC columns

进一步，分别选取层间位移角与牛荻涛模型损伤指数作为结构损伤指标，假定失效点转角对应层间位移角模型损伤指标，计算得到结构量化指标限值如表1．

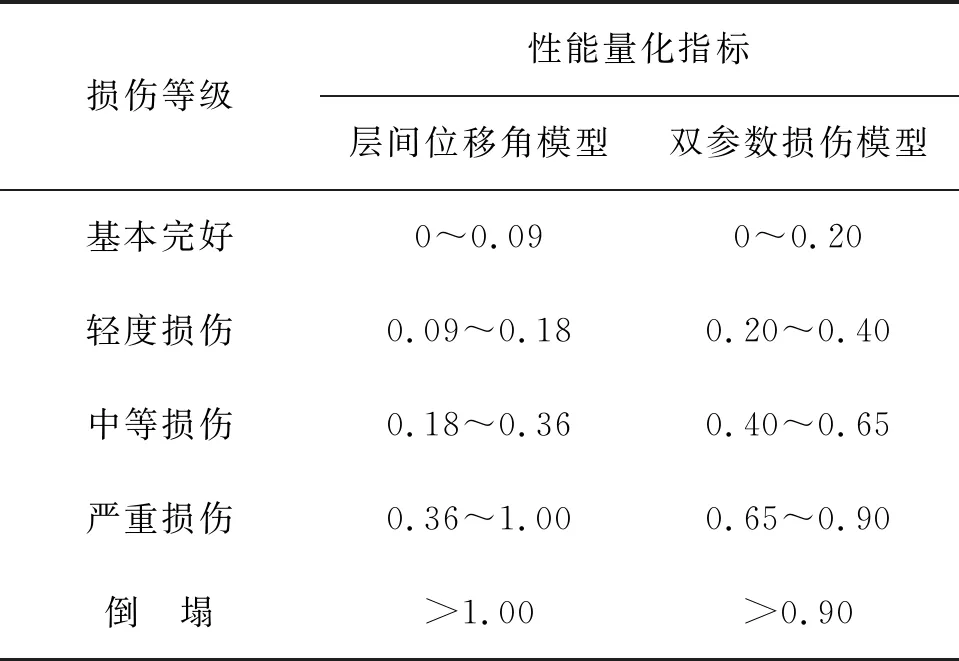
表1 结构地震性能量化指标限值

3 地铁车站结构地震易损性分析

3.1 增量动力分析

选用地面峰值加速度(peak ground acceleration, PGA)作为地震动强度指标(IM)，并分别调幅为0.05g、 0.10g、 0.20g、 0.30g、 0.40g、 0.50g、 0.60g、 0.70g、 0.80g和0.90g． 对土-结构模型进行非线性动力时程分析，得到200组结构地震响应数据样本．

首先，针对各地震动作用下地铁车站结构的最大位移反应，求得层间位移角模型和双参数模型的结构损伤指标分布情况，如图7．其中，LS1、LS2、LS3和LS4分别对应不同等级的结构损伤操作．

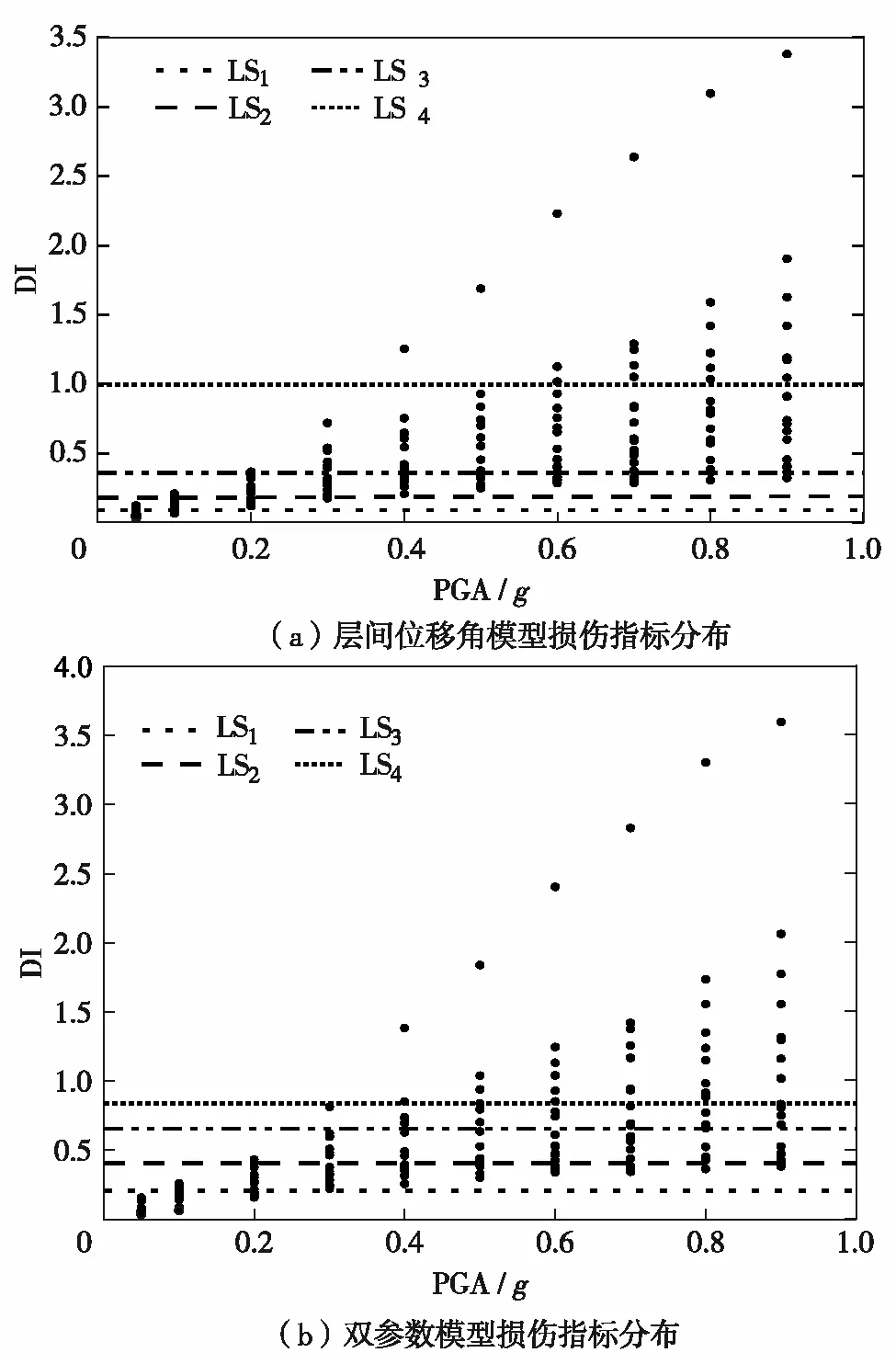
图7 地铁车站结构损伤指标分布Fig.7 (Color online) Structural damage index distribution of subway station

假定结构的地震需求指标(demand index, DI)与IM之间满足

ln(DI)=Aln(IM)+B

(2)

其中，A和B为回归系数.

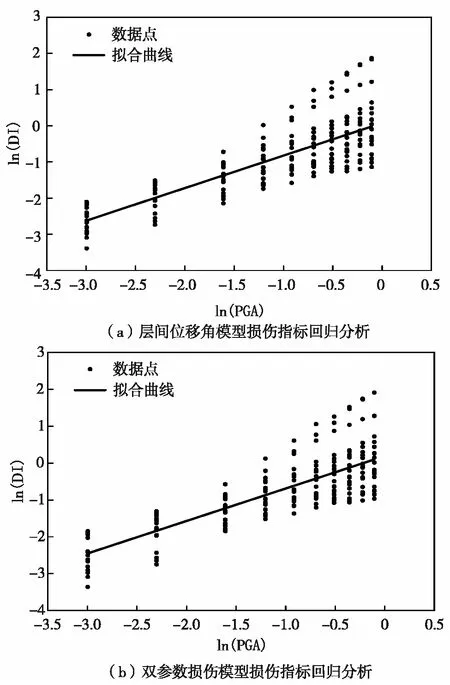
图8 地铁车站结构损伤指标回归分析Fig.8 (Color online) Regression analysis of structural damage index in subway station

然后，根据式(2)对结构损伤指标进行回归分析，建立地铁车站结构地震需求参数与地震动强度参数的关系(图8)．其中，层间位移角模型损伤指标与地面峰值加速度之间的关系式为

ln(DI)=0.898ln(PGA)+0.074 61

(3)

双参数损伤模型损伤指标与地面峰值加速度之间的关系式为

ln(DI)=0.881ln(PGA)+0.192 92

(4)

3.2 易损性分析

地震易损性即结构在不同强度地震作用下，超过某种破坏状态需求能力的条件概率，可表示为

(5)

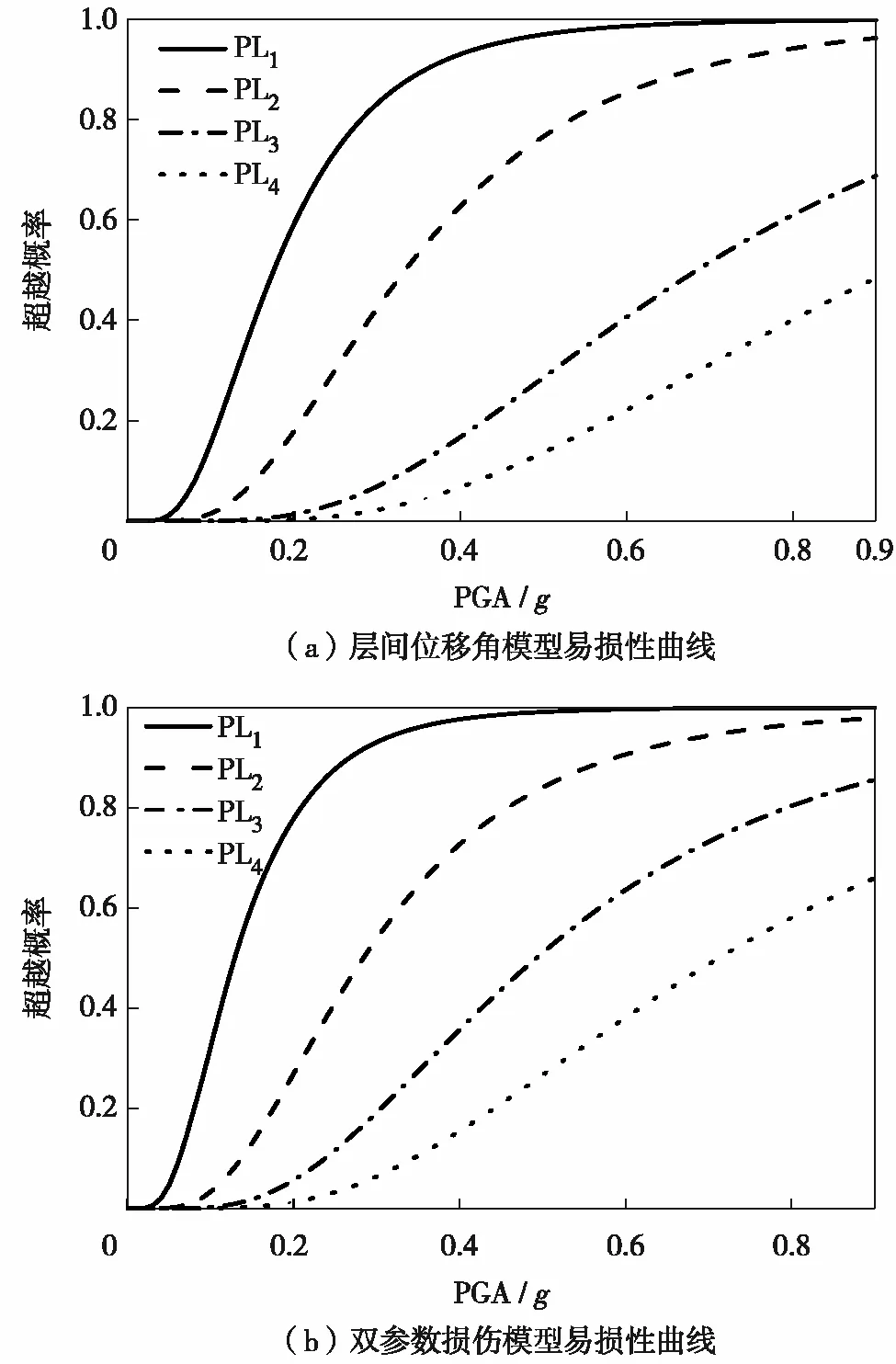
图9 地铁车站结构地震易损性曲线Fig.9 Vulnerability curves of subway station

图10 两种损伤模型的易损性曲线对比Fig.10 Comparison of vulnerability curves of two models

结合地铁车站结构性能的量化指标限值、地震需求参数与地震动强度的回归分析结果，建立地铁车站结构地震易损性曲线(图9)．图10为两种损伤模型在四性能水准状态下的对比曲线．根据易损性曲线，计算得到两种损伤模型在不同强度地震作用下针对不同性能状态的破坏超越概率，结果见表2和表3．由表2和表3可见：

1)针对轻度损伤与中等损伤状态，层间位移角模型与双参数损伤模型的超越概率比较接近， PGA<0.2g时，结构偏于安全，损伤以轻度损伤为主； PGA>0.20g时，逐渐向中等损伤过渡．

2)针对严重损伤状态，随着地面峰值加速度的增大，双参数模型的损伤超越概率从19.1% (PGA=0.30g)增长至85.6%(PGA=0.90g)， 层间位移角模型的损伤超越概率从6.9%(PGA=0.30g)增长至68.8%(PGA=0.90g)．说明层间位移角模型严重高估了地铁车站结构的抗震性能．

3)针对倒塌状态，在地面峰值加速度较小(PGA<0.20g)时，结构倒塌的概率接近于0，随着地面峰值加速度增大，双参数模型得到的结构倒塌概率远高于层间位移角模型，说明此时累积滞回耗能对结构损伤起到了关键作用．

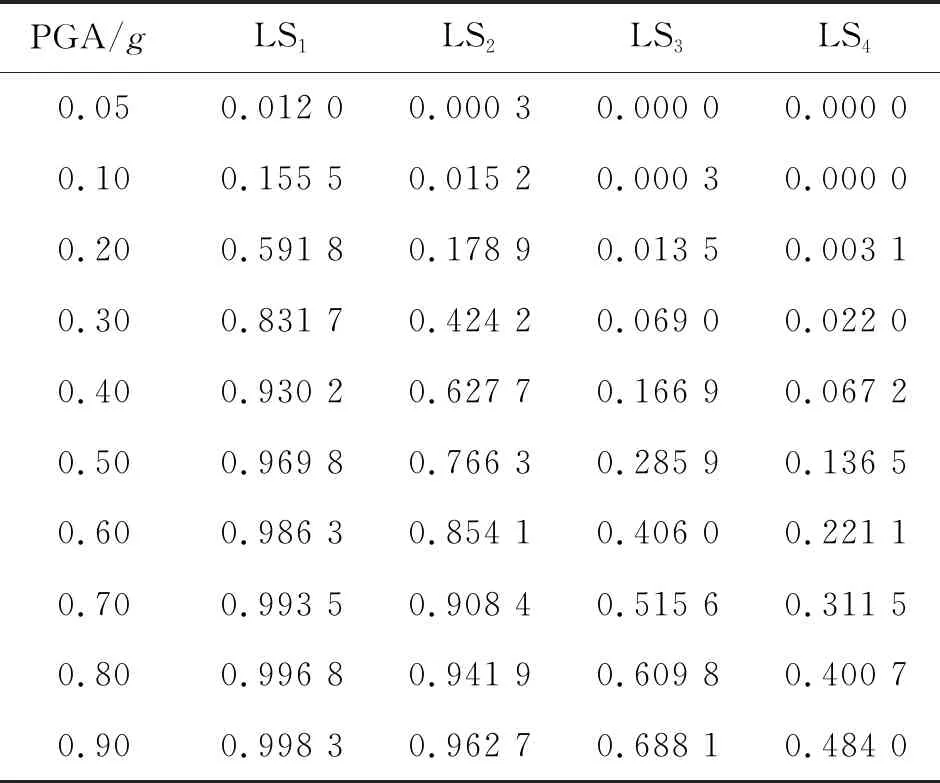
表2 层间位移角模型结构性能极限状态超越概率Table 2 Limit state exccedance probability of inter-story displacement drift angle model

表3 双参数损伤模型结构性能极限状态超越概率

4 结 论

针对某单层双跨地铁车站结构，建立了饱和砂土场地-地铁车站非线性动力体系数值模型．采用IDA方法对比分析了结构在两种损伤模型下不同破坏状态的超越概率，计算结果表明：

1)当PGA<0.20g时，结构偏于安全，损伤以轻度损伤为主；当PGA<0.20g时，损伤逐渐向中等损伤过渡．

2)仅以层间位移角作为地铁车站结构性能量化指标时，往往会高估结构的抗震性能．

3)结构损伤程度较轻时(轻度损伤和中等损伤)，最大变形对地铁车站结构损伤起主要控制作用；结构损伤严重时(严重损伤和倒塌)，累计滞回耗能对结构损伤起到关键作用．

4)双参数损伤模型对结构抗震性能计算结果较层间位移角模型更保守，更符合结构实际损伤情况．本研究建立的地震易损性分析流程，可为地铁车站结构的防灾减灾及抗震设计提供参考．