基于可视化编程环境的船型参数化融合与降阻优化研究
周 俊 秋,孙 风 胜*,张 维 英,于 洋,于 博 文,王 乐,隋 江 华,2
(1.大连海洋大学 航海与船舶工程学院,辽宁 大连 116023;2.大连市渔船安全技术工程技术研究中心,辽宁 大连 116023)
0 引 言
高效率、高质量的船体几何重构是船型优化问题中的重难点,如何使用尽量少的设计变量来产生大量的船型样本是船体几何重构追求的目标,而一系列不同船型的生成又伴随着型线光顺的挑战.设计一种结合可视化与参数化建模的船体几何重构方法是解决以上问题的关键.
在船体参数化建模技术的多种方法中,源于动画领域表示物种进化过程的融合技术可便捷地利用可视化技术来展现外形的过渡形状.1995年Doctors首次应用融合技术实现船型变换,通过将母型库中的船型进行融合而得到全新的船型,并指出该方法可进一步应用于船型优化[1].2006年,Tahara等首次将融合技术应用于型线优化,基于NAPA软件的二次开发和计算流体力学(CFD)对油船进行了型线优化[2].2007年,Yang等在船舶设计初始阶段采用融合技术,开发了型线及主尺度的并行设计模式[3].2010年,冯佰威等将直接操纵NURBS(non-uniform rational B-spline)曲面控制点(CV点)的方法和船型参数化融合方法进行了对比,得出船型参数化融合方法在母型船数量多的前提下可产生质量高且几何丰富的船型,优化效果较好[4].2018年,Zhang等基于曲面法采用可视化编程语言Grasshopper设计了球艏参数化几何重构的可视化程序,由程序控制的建模结果可在Rhino界面中实时更新[5].
采用融合技术可同时对若干不同船型进行融合,生成一系列全新的船型.可视化编程可通过程序参数化操纵NURBS曲面控制点的融合,并将几何重构结果实时地在图形界面上展现.本文基于可视化编程环境提出一种在新船型设计初期采用船型参数化融合技术将性能优秀的母型船型线对新设计船型进行几何重构的船型优化方案.通过取若干组该方案生成的不同艏部形状的船体进行静水阻力预报及选优,并给出一种在可视化编程环境下基于遗传算法的型线光顺方法,从而验证在船型设计初期基于可视化编程的船型参数化融合方法应用于船型优化的可行性.
1 型线与曲面的NURBS构造原理
NURBS曲线的有理分式表示为
(1)
式中:每一个控制点di(i=0,1,…,n)分别对应一个权因子wi(i=0,1,…,n).权因子越大,控制点对曲线的“吸引力”就越大,曲线越靠近控制点.Ni,k(u)是由节点矢量u=(u0u1…un+k+1)按deboor递推公式定义的k次(k+1阶)B样条基函数,i表示B样条的序号.deboor递推方法易于计算机程序的实现,其递推定义如下:
(2)
k次NURBS曲面有理分式表示为
(3)
式中:di,j(i=0,1,…,n;j=0,1,…,m)是曲面的控制点,呈拓扑矩形阵列,组成双向控制网格;wi,j是控制点di,j对应的权因子;四角点处用正权因子,即w0,0,wn,0,w0,m,wn,m>0,其余wi,j≥0;Ni,k(u)和Nj,l(v)分别表示u向k次和v向l次的规范B样条基函数.
当固定u、v向的节点矢量u=(u0u1…
un+k+1)和v=(v0v1…vm+l+1)时,船体曲面各点的型值由控制点的位置决定,可操纵控制点的空间位置进而使曲面变形,得到新的船体几何形状.
2 船型参数化融合的实例应用
2.1 母型船及其船型差异
本文使用基于NURBS的船型参数化融合技术对两艘母型船进行艏部融合,以两艘母型船体艏部几何外形作为边界,利用参数化控制每条船的融合系数即权因子的大小,进而生成一系列不同艏部几何形状的中间过渡船型.
两艘母型船分别是韩国KRISO海洋工程研究所的标准船模克里索集装箱船(KCS)和基于Rhino平台新设计的集装箱船初始设计模型船型A.图1是KCS和船型A的三维模型.

(a)KCS
表1是两艘母型船模的主尺度参数,母型船的主尺度参数由基于Grasshopper的船舶设计插件Nemo 1.1 Beta测得.

表1 母型船主尺度参数Tab.1 Main dimension parameters of the parent ship
图2是KCS和船型A的艏部几何差异.KCS是近些年在型线优化研究中的热门船型,其船型性能表现优秀,适合作为新船型设计的母型船.通过融合技术将KCS对船型A进行几何重构,为船型A在设计初期的型线优化及水动力性能研究提供充足的模型样本.
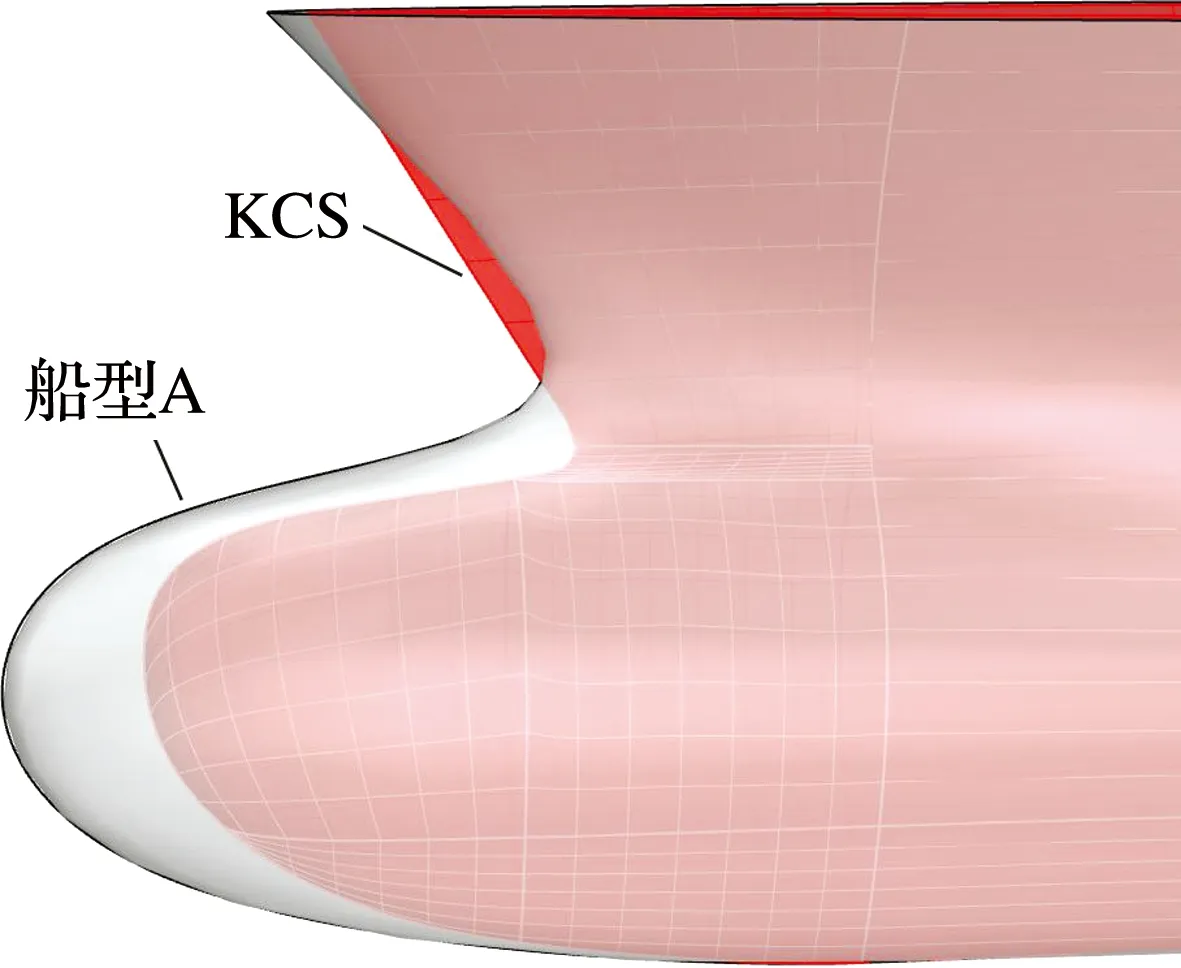
图2 KCS与船型A的艏部几何差异Fig.2 Geometric difference between the bow of KCS and ship type A
2.2 型线参数化融合
要实现KCS和船型A的艏部融合,通常采用的方法是操纵母型船的NURBS控制点进行合成,给定融合系数即给定了一个新的控制点.融合过程如下[4]:
(4)
式中:P为过渡船型的控制点坐标;PK为母型船的控制点坐标;N为母型船的数量;CK为融合系数.融合过程中,为将过渡船型控制在以母型船为边界的船型空间内,需设定融合系数的约束条件:
(5)
在生成新控制点后,产生过渡船型的方法通常有两种.第一种是采用新控制点产生船体曲面的网格,再进行由网格生成曲面的逆向工程.第二种是根据控制点位置重新绘制NURBS曲线,生成新的型线,进而由新型线建立过渡船型的NURBS曲面.由于通过网格转换生成的NURBS曲面面片之间的过渡一般为G1连续,而通过光顺的型线建立的模型一般可实现G2连续,本文采用第二种方法建立船型A的过渡船型.
图3(a)所示为在同一横截面位置从KCS及船型A的船体上分别截取的一段横剖线,左边(船型A)的横剖线为1 558个控制点的3阶NURBS曲线,右边(KCS)的横剖线为66个控制点的3阶NURBS曲线.由于实现两根横剖线的融合,需要两根横剖线的控制点数量相等,通过融合系数将两根横剖线的控制点对应合成,进而生成新控制点.曲线的控制点数量越多,曲线质量越低,调整曲线形态对其内部连续性的影响越大,且曲线阶数越高其内部连续性越好[6].故在进行融合操作前需要对两根横剖线进行NURBS曲线重建,使两根横剖线的控制点满足实现融合的条件.曲线重建后的两根横剖线如图3(b)所示,船型A及KCS的横剖线都为24个控制点的6阶NURBS曲线.
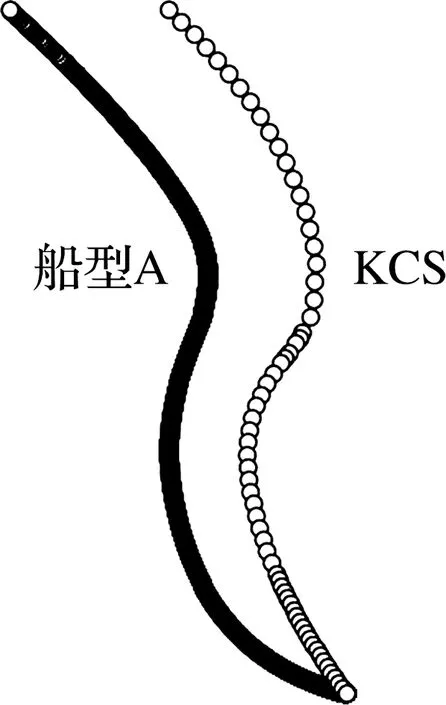
(a)重建前的横剖线
本文基于可视化编程环境Grasshopper进行船体曲面的融合程序设计.对图3(b)中成对的NURBS曲线控制点进行合成及生成新NURBS曲线的Grasshopper程序如图4所示,该程序生成的新控制点及NURBS曲线在Rhino平台实时展现.部分不同融合系数的新控制点及其横剖线如图5所示,可以看出分配给船型A的融合系数CA越接近1.0,新横剖线越偏向于船型A;CA越接近0,新横剖线越偏向于KCS.
2.3 新设计船型的船体几何重构
在融合两艘母型船的艏部曲面前需要找到两艘母型船体共有的边界线,如图6所示,边界线将两艘母型船体分为主船体和艏部曲面两部分.
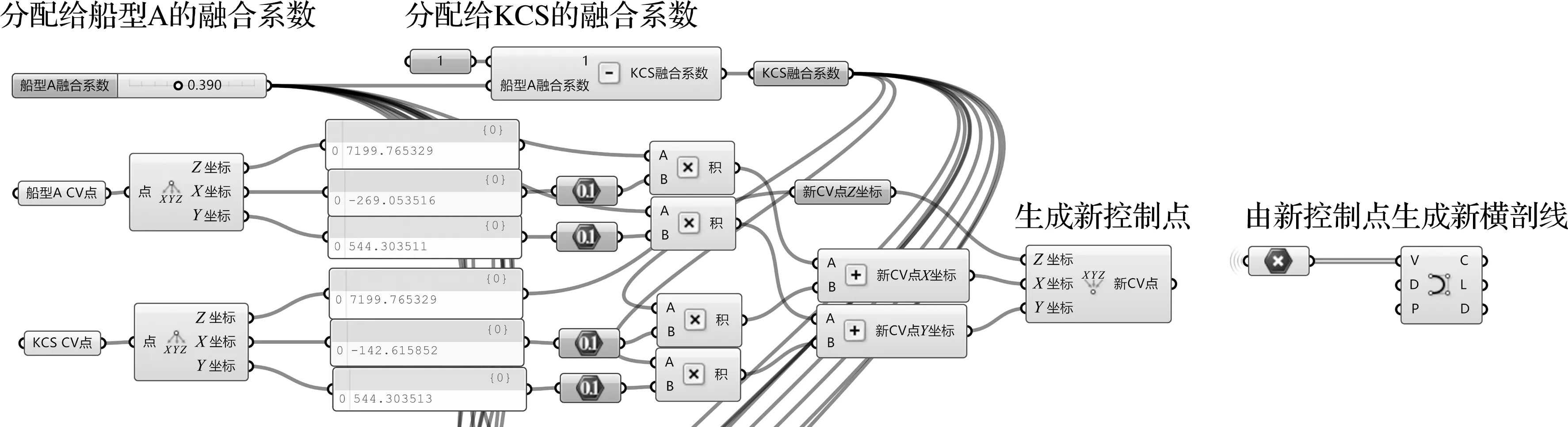
图4 控制点融合及新横剖线生成程序Fig.4 Control point fusion and new body lines generation program
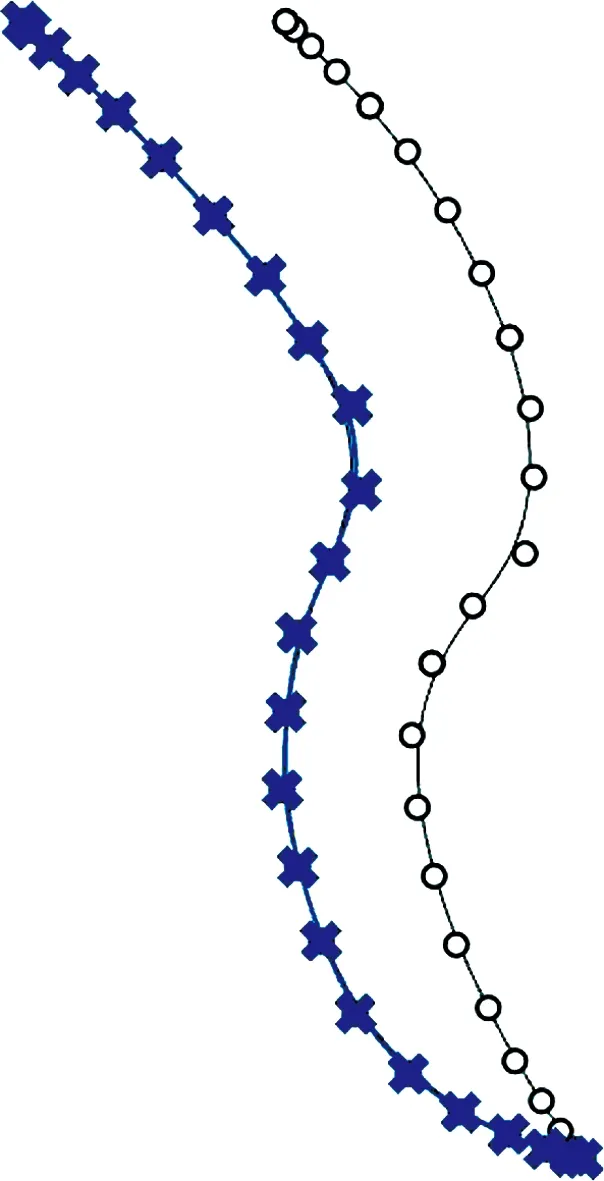
(a)CA=1.0
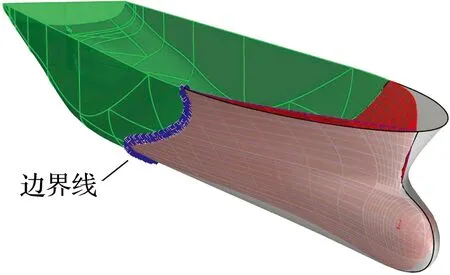
图6 母型船艏部边界线Fig.6 Parent ship bow boundary line
两艘母型船的艏部曲面分割出来后,为两艘母型船体的艏部曲面在相同横截面位置和相同水线高度处分别绘制横剖线及水线,生成的型线如图7所示.在Rhino平台中提取两艘母型船体的艏部轮廓线作为基本结构线.
图7中,为了满足控制点对应融合的条件,通过Rhino平台对母型船的型线及基本结构线进行NURBS曲线重建,使两艘母型船相互对应的型线及基本结构线的控制点数目和阶数相等.
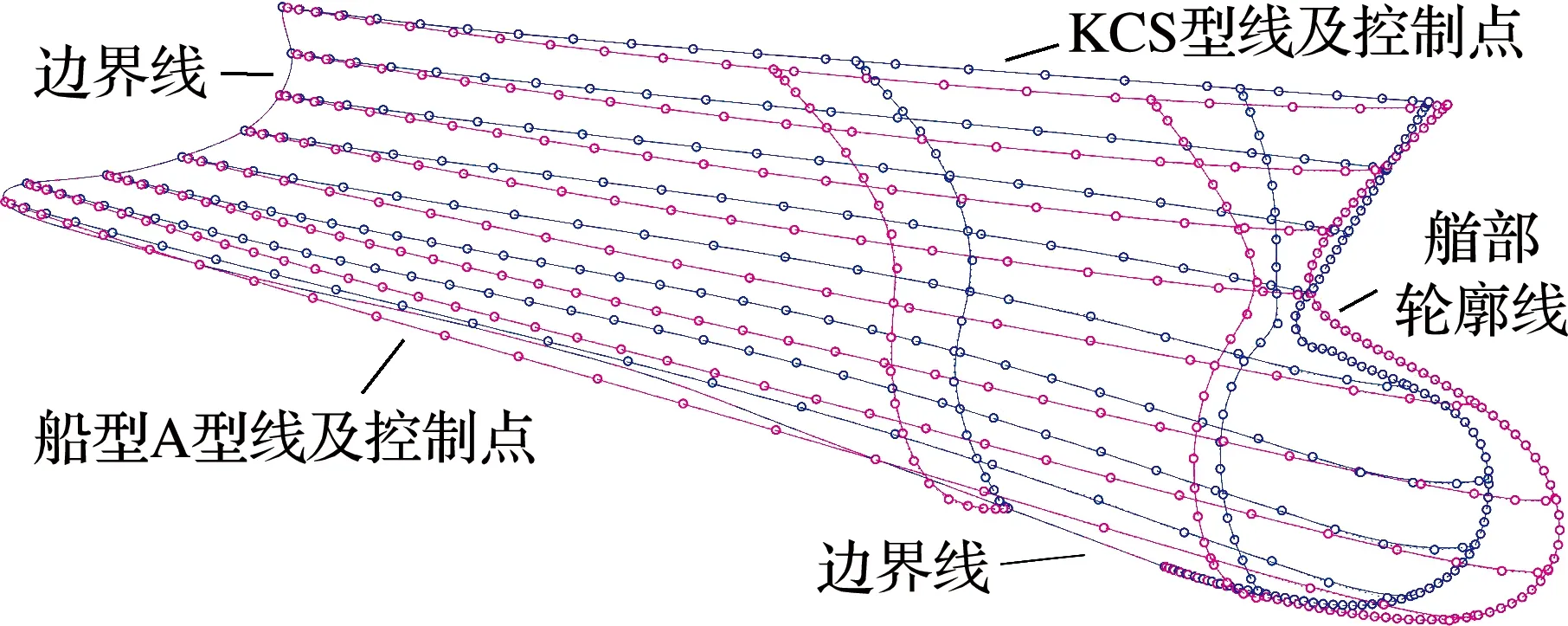
图7 母型船的型线示意图Fig.7 Schematic diagram of the parent ship′s profile line
基于可视化编程环境Grasshopper搭建对母型船的对应型线及基本结构线中对应位置的控制点进行融合的程序,进而生成与母型船艏部型线及基本结构线的控制点数目和阶数相同的过渡船型型线及基本结构线,该过渡船型型线可完全实现参数化控制.如图8所示,过渡船型的各条型线之间的控制点分布合理且均匀,型线质量较高.
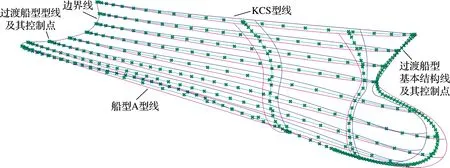
图8 过渡船型型线及基本结构线Fig.8 Transition ship profile line and basic structure line
基于过渡船型型线及基本结构线建立过渡船型艏部曲面,参与构建曲面的曲线的阶数和控制点数量及其分布越一致,所生成的曲面的连续性越高,进行曲面修改及重构的难度越低[6].通过Grasshopper的融合系数滑块控制船型A与KCS的融合比例,进而可生成一系列不同融合系数的过渡船型艏部曲面,将该曲面与船型A的主船体合并生成完整的船型A过渡船型.部分不同融合系数的船型A过渡船型球艏曲面如图9所示.
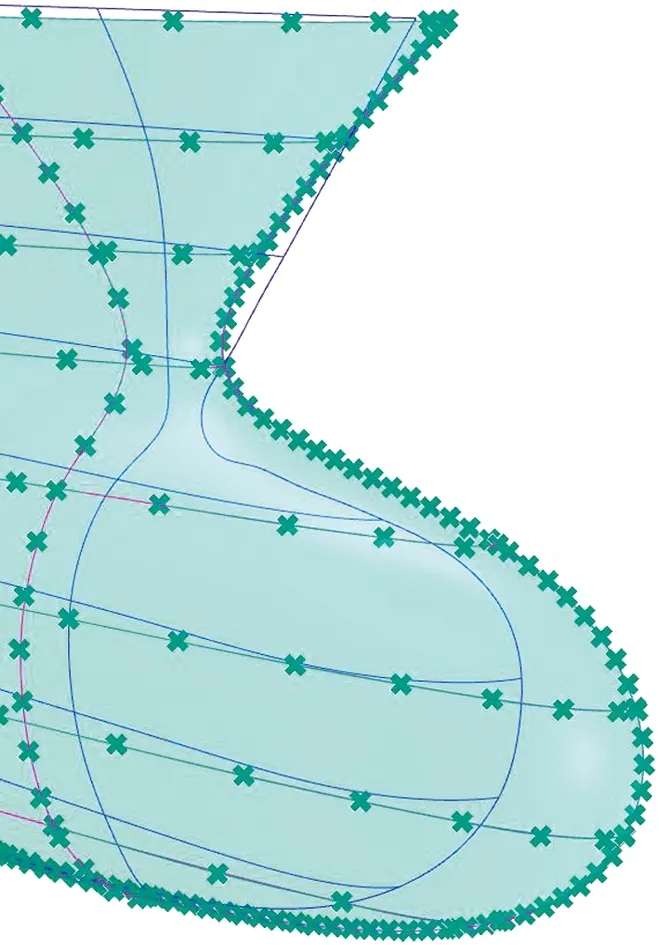
(a)CA=1.0
3 船型融合及其在船型优化的应用
3.1 基于Holtrop法阻力预报的降阻优化
船型参数化融合生成的一系列过渡船型可作为型线降阻优化的样本,进而可通过寻优算法进行设计变量的寻优,得到阻力最优的船体型线.本文为了验证基于可视化编程环境的船型参数化融合技术在型线优化上的可行性,使用船舶设计插件Nemo 1.1 Beta对通过基于Python语言编写的拉丁超立方抽样(LHS)试验设计法程序抽取的多组不同设计变量(融合系数)的过渡船型进行阻力预报.图10是Nemo的阻力预报可视化程序模块,该模块基于Holtrop经验公式法对船体NURBS曲面进行阻力计算,Holtrop法可定性评估船模尺寸的船体阻力[7].Holtrop法总阻力表示为[8-10]
Rt=Rf(1+k1)+Rapp+Rw+Rb+Rtr+Ra
(6)
式中:Rt是总阻力;Rf是依据ITTC 1957公式所计算的摩擦阻力;1+k1是船体形状因子;Rapp是附体阻力;Rw是兴波阻力;Rb是球艏引起的附加压阻力;Rtr是艉封板浸没引起的附加压阻力;Ra是船模与实船相关修正阻力.
船型A(CA=1.0)、KCS(CA=0)及通过LHS抽取的10组不同CA的船型A过渡船型在弗劳德数Fr=0.28时的Holtrop法阻力预报数值如表2所示.
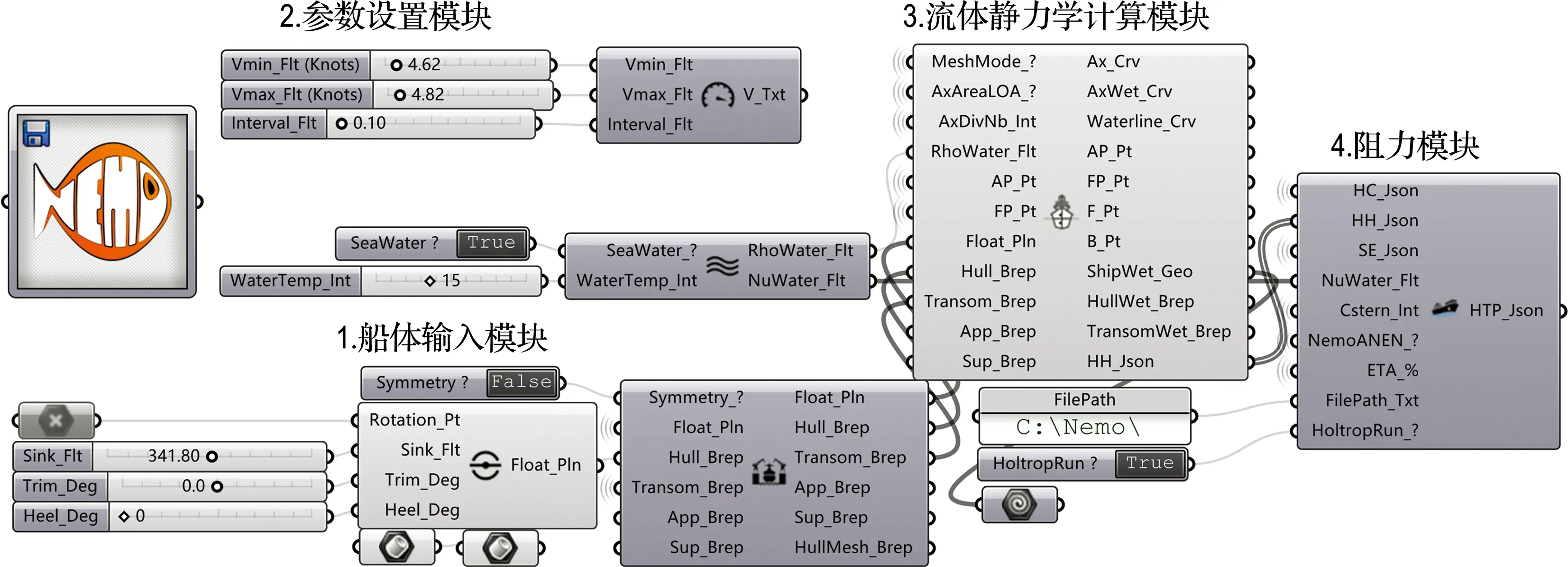
图10 Nemo的阻力预报程序模块Fig.10 Nemo′s resistance prediction program module
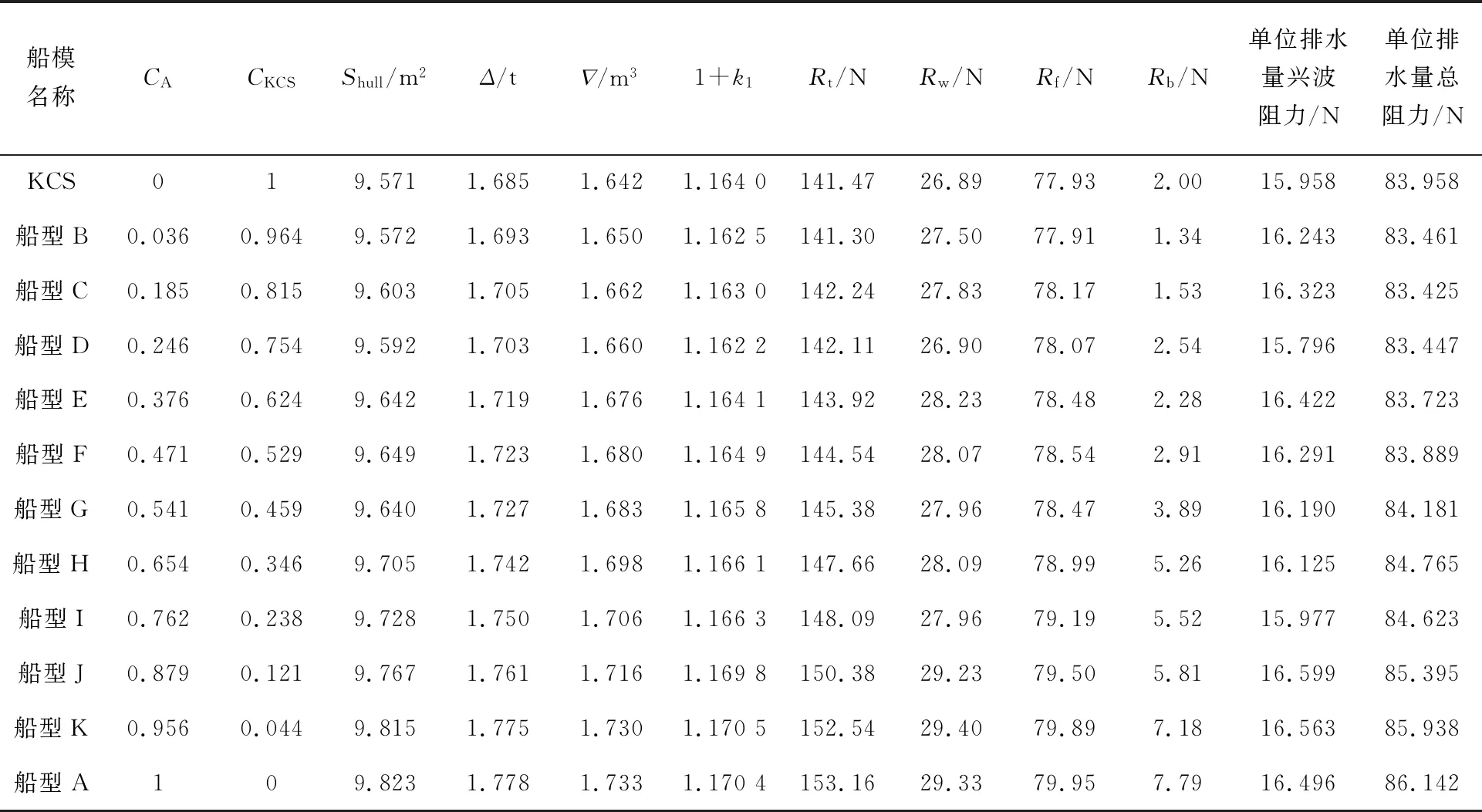
表2 母型船及过渡船型的Holtrop法阻力预报结果Tab.2 Resistance prediction results of the Holtrop method for the parent ship and transition ship type
通过Holtrop法公式推算出Rf与船体湿表面积Shull呈正比例关系[7].船型A的艏部形状较KCS丰满,随着分配给船型A的融合系数CA逐渐减小,过渡船型的艏部几何外形逐渐趋向KCS,Shull随之减小,故Rf也逐渐减小.
根据Holtrop法的推论[7],航速v与艏吃水Tf一定时,Rb仅与艏垂线处的球艏横剖面积Abt及横剖面形心到基线的高度Hb有关.观察图8中过渡船型的艏部几何形状,随着CA的增大,过渡船型Abt及Hb发生连续且规律的变化,故Rb与CA间的线性关系显著.
KCS的艏部设计水线较船型A瘦削,进流角相对小,更有利于Rw的降低.且KCS的球艏较船型A瘦削,故随着CA的减小,过渡船型的球艏形状逐渐瘦削,导致破波阻力减小,而破波阻力本质即属于兴波阻力[7].
由表2可知,船型D的单位排水量兴波阻力在包括母型船在内的12组样本中表现最优,单位排水量兴波阻力为15.796 N,单位排水量总阻力为83.447 N.船型C的单位排水量总阻力在包括母型船在内的12组样本中表现最优,单位排水量总阻力为83.425 N,单位排水量兴波阻力为16.323 N.船型D与船型C的总阻力性能均较优,但船型D的兴波阻力性能明显优于船型C,船型D更有利于集装箱船的高速航行.故船型D可作为本次优化设计的优选船型.
船型D的型线充分地融合了KCS的特点,实现了对母型船——船型A的型线降阻优化,验证了在船型设计初期基于可视化编程环境的船型参数化融合技术应用于型线优化的可行性.图11(a)是船型D的三维造型,图中显示了通过Rhino平台中的光照斑马线对船模进行曲面质量视觉检测的情况,斑马线在多重曲面连接处的过渡较光滑,较少出现曲率突变,通过船型参数化融合技术生成的船体三维曲面质量较高.图11(b)是船型D的型线图.

(a)船型D的三维造型及斑马线示意图
3.2 基于遗传算法的可视化型线光顺
船型融合后生成的新型线(NURBS曲线)存在不光顺的情况,需要在建立船体曲面前先对型线进行光顺,以保证建立的过渡船型曲面质量满足型线优化中船舶性能数据计算的要求.本文在前人已有文献的基础上应用遗传算法通过可视化编程实现型线光顺,寻优过程中型线发生的变形实时地在Rhino平台图形界面上显示,遗传算法在寻优过程中直接对NURBS控制点的最佳位置进行搜索,整个优化过程十分直观,操作较为简便.
光顺的曲线不存在奇点和多余的拐点,且曲线曲率变化均匀,曲线的变形能较小.采用能量优化法,将曲线NURBS控制点坐标的最大修改量作为约束条件,基于遗传算法对控制点的位置进行寻优是型线光顺的有效方法之一.能量优化法以曲率的平方和为能量函数:
(7)
式中:κ为所求以u为参数的曲线的曲率.从上式中可以得出[11],能量较小可以粗略地理解为平均绝对曲率较小,所以曲线的光顺在宏观上可理解为曲线趋向直线变化.
本文基于可视化编程环境Grasshopper设计了基于遗传算法的型线光顺程序,寻优程序的核心采用Galapagos运算器,程序主要模块布置如图12所示.
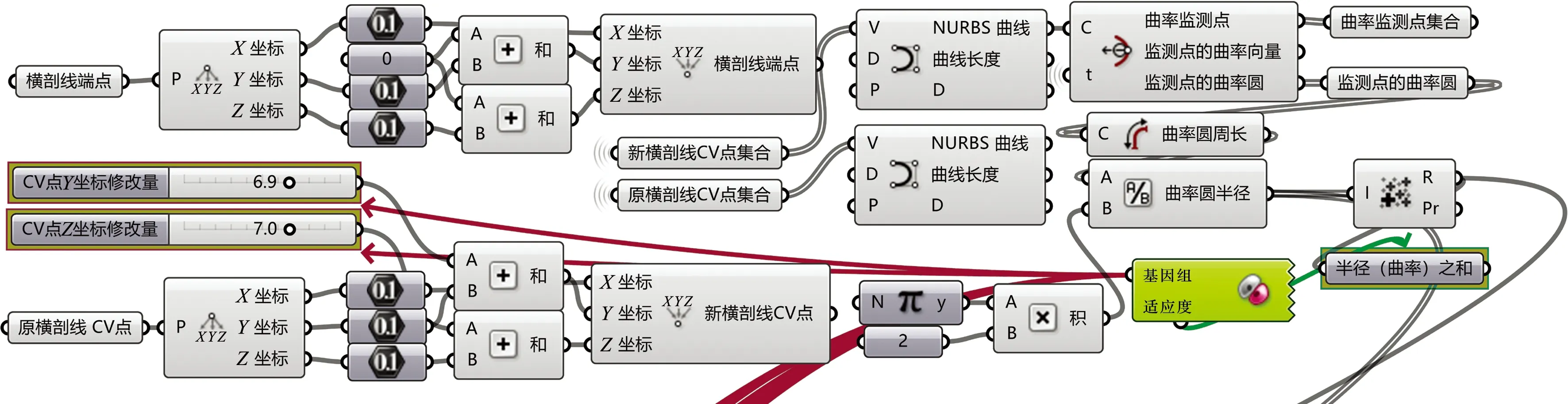
图12 基于遗传算法的型线光顺可视化程序主要模块布置Fig.12 The layout of the main modules of the visual program for profile line smoothing based on genetic algorithm
该程序将NURBS曲线控制点坐标的最大修改区间设置为[-20,20] mm并作为约束条件,以控制点坐标的修改量作为自变量.在NURBS曲线上取60个等间距的曲率监测点,以所有曲率监测点的曲率圆半径之和作为适应度,监测点上的曲率圆半径即曲线在该点处曲率的倒数.通过遗传算法对控制点位置进行寻优而实现使整条曲线上所有监测点曲率半径之和最大,即使曲线上各监测点曲率都尽可能最小,进而消除曲线上的拐点,使曲线趋向直线变化,达到光顺的目的.
本文以船型B艏部的一根不光顺的横剖线为例进行型线光顺优化,原始横剖线如图13(a)所示.优化过程分为3个阶段:第一阶段通过型线光顺可视化程序进行初级寻优,历时10 min,运行到1 484代时寻优停止,得到了初级的型线优化结果,此时适应度最大值为2.038 1×109,初级优化的横剖线如图13(b)所示,该横剖线较原横剖线光顺,但仍存在拐点等曲率较大的地方;第二阶段继续通过该型线光顺可视化程序进行寻优,在优化程序中将初步优化的横剖线控制点坐标设置为初始位置,历时4 min,运行到100代时寻优停止,得到了第二阶段的型线优化结果,此时适应度最大值为1.764 9×108,二级优化的横剖线如图13(c)所示,该横剖线拐点消失,较初级优化结果更为光顺;第三阶段,直接将第二阶段的横剖线在Rhino平台中保持阶数不变进行减小控制点的曲线重建操作,即得到满足质量要求的光顺型线,最终的横剖线如图13(d)所示.
第一及第二阶段的优化迭代过程中最优个体如图14所示,图中红色点代表每代中的最优个体.
第一及第二阶段的优化迭代过程中,型线及曲率监测点的曲率圆变化情况如图15所示,随着遗传算法对自变量的搜索,型线及各监测点的曲率圆也在Rhino平台的图形界面动态变化.
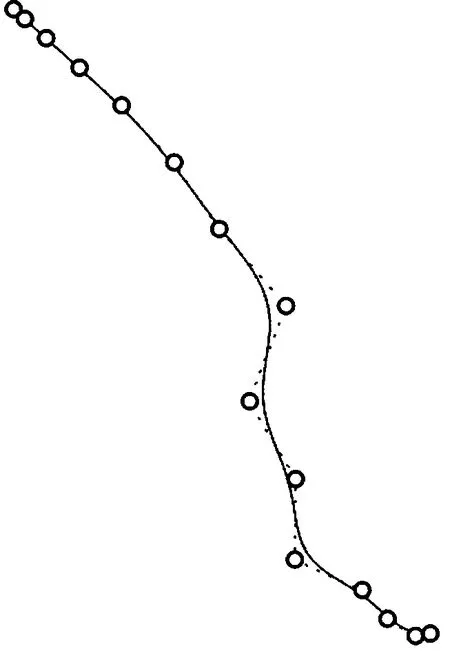
(a)原始横剖线
(a)第一阶段1 401代最优个体
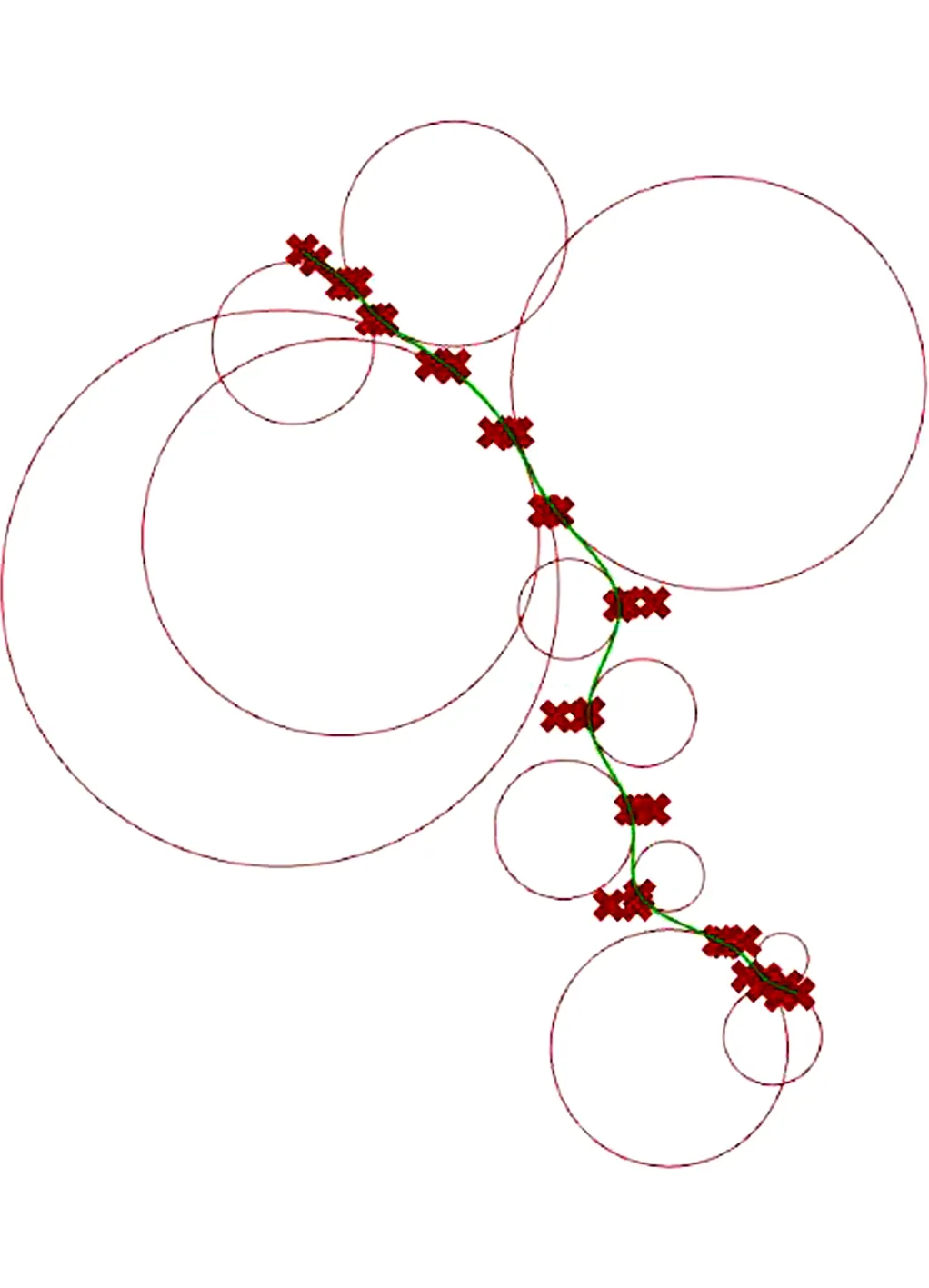
图15 型线及曲率圆变化情况示意图Fig.15 Schematic diagram of the change of profile line and circle of curvature
4 结论与展望
本文基于可视化编程环境使用Grasshopper语言将性能优秀、设计成熟的KCS母型船对一艘新设计的集装箱船进行船型参数化融合,以融合系数作为单一设计变量进而产生一系列参数化样本模型,越少的设计变量产生越充足的样本的过程是船体几何重构追求的目标和难点[12];船型融合中过渡船型的生成是完全基于参数化的,且可视化程序记录了曲线及曲面生成的逻辑关系,做到了给定设计变量数值即可自动产生对应的船体三维模型,并保证船体几何重构后的光顺性.
通过集成了Holtrop法的可视化程序模块对经融合生成的若干组过渡船型进行阻力预报并从中选优,验证了船型参数化融合技术应用于船型优化的可行性.该程序模块直接对一系列船体模型进行快速阻力预报,极大地方便了设计初期船型优化过程中船舶性能的计算,节省了设计时间.
本文设计了一套基于可视化编程环境的型线光顺程序,使集成了遗传算法的运算器可以直接对图形进行自动寻优操作,型线光顺的过程在图形界面中动态显示,该程序优化时间短且效率高,为解决船型融合等船体几何重构方法中的型线不光顺问题提供了新的解决方法,验证了基于可视化编程环境的船型参数化融合方法应用于船型优化的可行性.
有几点思路值得开展后续的研究:融合技术对船型的重构不能精确地指定船体部位,可通过直接操纵控制点改变其位置坐标进行具体部位的几何变形;有待采用计算流体力学(CFD)结合Holtrop法进行变精度阻力预报,大幅提升预报精度,并降低计算耗时[13];型线光顺的可视化程序中可添加曲率变化率(曲率的一阶导数)这一新的目标函数,进行型线光顺的多目标优化.
——福船

