CNN边缘影响分析与改进的语音识别

方园园，朱 敏

（南京航空航天大学，江苏 南京 210016）

0 引 言

近年来，随着人工智能的发展，自动语音识别技术（Automatic Speech Recognition，ASR）也被不断研究与发展，并被应用到各种不同的领域，例如：声音驱动指令、人机界面、相关文本翻译以及医疗超声[1⁃8]等，为人类生活带来了巨大的便利。语音识别技术在发展的过程中，其相关研究几乎都致力于相关模型算法的优化。被应用广泛的模型有隐马尔可夫模型（Hidden Markov Model，HMM）、短 时 记 忆（Long Short⁃Term Memory，LSTM）网络、深度神经网络（Deep Neural Network，DNN）以及卷积神经网络（Convolutional Neural Network，CNN）等，多年来被不断地改进来改善语音识别率。例如：文献[9]关于LSTM、DNN和CNN的各自优劣将它们组合成一个改进模型CLDNN；文献[10]致力于改进代价与激励函数来生成一个新的CNN改进模型，提高语音准确率。但是，网络模型的优化会涉及层数的加深和模型结构的复杂化，这样不但会使得实验中计算和算法相对复杂，也可能会造成网络训练中的过拟合。

作为当今语音识别深度学习模型的主流，CNN具有局部卷积及池化的显著特点[10]，通过对一定量的视觉图像的分析学习，来达到图像识别、语音处理[11]和推荐系统[12]等的效果。此模型常以二维或三维图像为输入数据，并且对此类结构的信息非常敏感，也是现如今广泛用于计算机视觉领域的网络模型。对于基于CNN的语音识别技术，现有的研究大多将表示为时域和频域的二维形式的语音特征直接输入到CNN或是改进优化的CNN中。在本次实验中，通过观察大量经过语音活动检测（Voice Activity Detection，VAD）等预处理的二维语言特征，发现大多特征存在非零特征区域边缘化的特点，即大多数非零特征区域位于整个二维特征的边缘位置。这样的特点会造成在CNN的训练阶段中，因为CNN中的局部卷积和池化的特点，语音特征中边缘区域信息丢失，从而大幅度降低CNN语音识别的准确率。在本文中，将由于非零特征区边缘化造成的影响称为边缘影响，并针对该影响展开了研究，认为解决该边缘影响的方法应起到将非零特征区域“移动”到远离边缘位置的效果。本次实验采取了几种几何改进方法来缓解边缘影响，通过相同的CNN结构以及训练时长在自录制与公共数据库的混合数据的识别准确率，证明了经过几何改进的二维特征，在CNN中的识别性能都优于存在边缘影响的原始特征。

1 特征提取

在关于CNN的语音识别中，语音特征的提取过程通常如图1所示。语言特征提取过程包括对标准数据库的数据获取及生成数据语音帧，再让每一帧语音经过梅尔滤波器生成不同频率带宽的能量特征值，最后将得到的二维特征放入卷积神经网络进行训练。

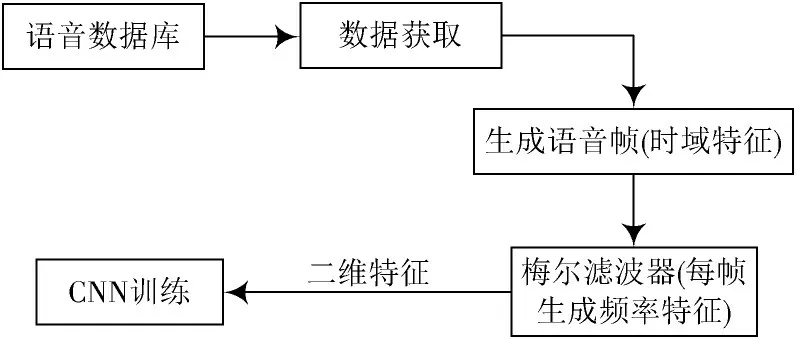
图1 二维语音特征提取步骤结构图

1.1 数据获取

数据获取的主要内容是预处理和数据幅值的缩放[13]，例如归一化和去噪等部分。文献[14]在获取数据库时，采用了二次采样、归一化去直流以及语音活动检测（Voice Activity Detection，VAD）的方法，便于之后语音特征提取等操作时，不受周围噪声等的干扰，也方便数据库中大量语音的统一操作。从文献[15]可知，对于经过归一化去直流的语音数据，所提取的一维梅尔特征在人工神经网络（Artificial Neural Network）的训练效果并不理想，鲁棒性较差。经过对大量该类语音的观察，发现语音之间的开始和终止时间差异较大。此外，在未发音阶段也存在周围环境的声音（噪声）。这些因素都会影响语音识别的正确率和鲁棒性。为了区分人声部分和无声部分，VAD被应用来提取每段语音的人声部分，使得每段语音数据的开始和终止时刻更加统一，也可以去除周围噪声造成的干扰。如图2所示，对来自于第一个男性的语音数据“eight”（Speech，如图2实线所示），计算对应的短时能量（Short⁃Time Energy，STE），如图2虚线所示，并通过设定的阈值来筛选人声部分。在图2中，STE值与原始语音数据一一对应，所有与高于阈值的STE值时间点相同的语音数据，都会被提取出来，作为新的语音数据，用于后续处理。

图2 归一化的短时能量与语音数据结构图

1.2 梅尔倒谱系数

梅尔倒谱系数（Mel Frequency Cepstral Coefficients，MFCCs）是应用最为广泛的语音特征提取方法之一。采用该系数计算所需的滤波器组，梅尔滤波器组（Mel Filter Banks，MFBs）是经由大量实验所得的一系列频谱带宽，这些滤波器的带宽大小，反映了人耳对于不同语音频率带宽的敏感程度。语音频率值与梅尔频率值正、逆变换公式分别为：

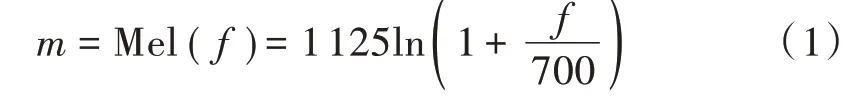
式中，f和m分别为频率值和梅尔刻度值。

将语音频率的上、下限值先经由（1）变换为梅尔频率的上、下限值，再根据所需梅尔滤波器个数进行等份，等份而得的梅尔刻度再经由式（2）得到梅尔滤波器的边缘值与中间值。本文根据所选取的语音数据库，取32个频率滤波器以及一个最大频率范围，即最低频率300 Hz和最高频率4 kHz；再根据这两个频率最值经由梅尔变换得到梅尔刻度范围，并将该范围划分为32个等份即34个梅尔刻度值，如式（3）所示；最后再应用梅尔逆变换由梅尔刻度得到频率值，最后得到如图3所示的32个三角形梅尔频率滤波器。

图3 32个梅尔频率滤波器

2 边缘影响分析

2.1 特征生成

本文在提取生成语音特征时，经过多次试验后决定的一些参数如下所示。首先是在数据获取阶段中的VAD部分，经过多次尝试，本文选择了0.02的阈值。在实际操作中，将STE值高于0.02的第一个数据点所对应的相同时间的语音数据会被作为新的初始点，而此点之后的所有数据将会被保留。以内容为“seven”的男性录音为例，原始语音数据与VAD处理之后筛选出来的人声部分的对比，如图4所示。经过VAD之后，人声部分在本文中的语音特征被表现为二维的形式：时域坐标和频域坐标[11⁃12]。在经过滤波器之前，以50%的重复率将语音分成多个语音帧，然后将每一帧语音通过32个梅尔滤波器，计算各自不同时域的频率能量特征。需要注意的是，与一维特征的情况不同，二维特征除了频率坐标系之外，还要表示时域上的坐标。通常的梅尔倒谱系数计算是通过梅尔滤波器的语音能量，再经由离散余弦变换（Discrete Cosine Transformation，DCT）和对数变换而得。但是DCT反映了被映射在另一个基（basis）的音谱信息，而非传统的时域坐标。从而造成能量值的偏移，影响特征在CNN中的局部提取[10]，所以本文将DCT部分去掉。去掉DCT而计算得到的特征，称为MFSC特征[16]。生成的二维语音特征的表示如图5所示（“nine”，male，32×32）。

图4 VAD前后的语音数据

图5 MFSC二维语音特征

2.2 特征边缘化

在实验初期，将经过归一化去直流和VAD的语音信号进行特征提取，得到的部分二维特征如图6所示，在CNN中的识别效果并不理想。其CNN模型的改进，例如激励函数和层结构的加深，也未能改进CNN对所得二维特征的识别效果。

图6 男性与女性二维语音特征（32×32）

经过观察CNN中每一层卷积层或者池化层的输出，发现大量的特征在经过卷积和池化层之后，所得的输出图大部分都看不出明显的特征效果，如图7所示。经分析，主要原因是大量特征的非零特征区域处于整个特征图的边缘位置。在具有局部卷积及池化等明显特征[10]的CNN模型中，会使得这些非零特征在卷积层或池化层的响应不明显。这样，CNN的边缘化影响会大大降低CNN语音识别的正确率。

3 特征几何改进

为了减小卷积的边缘化影响，本文采取相应的几何改进措施，将非零特征区域“移动”使之远离边缘区域，这样才能让卷积层以及池化层得到更多特征部分的响应。本次实验采取的措施分别为几何对折、双线性插值、零值填充和翻折填充，下面将介绍这几种几何改进措施。

3.1 几何对折

以图6a）左侧的初始特征为例，将该特征在水平、竖直和对角线方向上进行对折，得到了如图8所示（男性，“nine”）最右方的对折特征。可以看出，通过几何对折的方式，虽然特征被复制，但是非零特征区域还是被完整地“移动”到二维特征值的中心位置。

图8 几何对折过程

3.2 双线性插值

双线性插值在图像处理中比较常见，本次实验采用双线性插值（Bilinear Interpolation）。通过该方法，可以改变图像的尺寸，但不会造成图像很大的变化。如图9所示（男性，“nine”，左男性，右女性），将图6a）进行双线性插值，非零特征区域的“形状”并没有太大改变。

图9 双线性插值特征

在双线性插值的具体施行中，因为输入和输出图像尺寸不同，分别为wi，hi（输入图像的宽、高）以及wo，ho（输出图像的宽、高），所以由宽和高的尺寸系数，可得到新像素点坐标(x,y)，其中，x，y分别为：

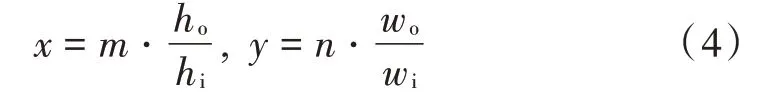
式中(m,n)表示输出图像对应的输入图像的位置点。值得注意的是x，y基本上为浮点数，所以新图像的像素点坐标应该是取其整数的(x′,y′)。

以上是关于得到新图像的像素点坐标，而得到的对应灰度值为：

在本次实验中，经过双线性插值的二维特征取得的识别正确率要比初始特征改善许多，但仍然没有达到理想的标准。

3.3 零值填充

零值填充是将初始特征的周围填充零值，如图10所示（“nine”，左男性，右女性）。图10a）的初始特征，在经过零填充后，非零特征值不会在左上角位置，视觉上会感觉往中心方向“移动”了一些。根据CNN中卷积层的核尺寸，本次实验尝试了两种大小的零值填充特征，分别为64×64和48×48，不难看出，图10a）的非零特征区域相较于图10b）要更远离边缘区域。

图10 零值填充特征

3.4 翻折填充

在本次实验中，“翻折”不同于“对折”，不是将整个初始特征进行复制，而是将特征的一部分（选取含有非零特征的部分），在水平、竖直和对角线方向上进行翻折。如图11所示（“nine”，左男性，右女性），选取非零特征中的8行和16行以及完全翻折的几何对折的不同。其中，形成的特征尺寸大小同样也是基于CNN卷积层的核尺寸。从图11可以看出，翻折特征与几何对折特征有一个很大的不同，就是特征区域的不完整。虽然包含了初始特征的部分，但是部分被翻折的特征处于整个特征图的边缘。

图11 翻折填充特征

4 卷积神经网络

本文基于对CNN相关知识的学习[17]，进行了CNN的设计。此节将会涉及CNN的学习过程以及本次实验具体设计CNN的细节。

4.1 网络结构

图12展示的是训练数据中的一个特征（“eight”，女性）经过几何对折的特征图经过CNN向前传播的过程。为了清楚表示几何改进方法的效果，本次实验中对于每一种改进特征都采用相同结构的CNN模型，CNN模型结构可以用以下序列表示，[I1,280,C2,10,P3,10,C4,20,P4,20,F5,150,F6,50,F7,10]。其中，I，C，P和F分别表示输入层、卷积层、池化层和完全连接层，其下标中的第一、二个数字分别表示它们位于CNN的第几层和尺寸大小，例如：C2,10表示CNN中的第二层为卷积层，卷积核大小为10×10。值得注意的是，与图7比较，经过相同的层结构，几何对折特征的“信息”比初始特征要明显。

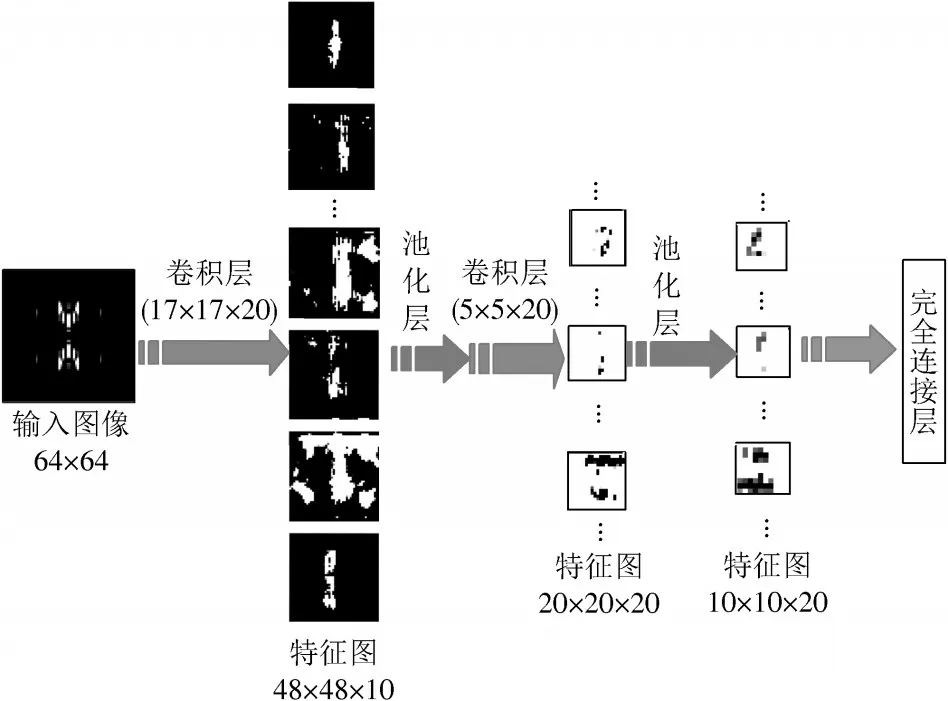
图12 CNN向前传播结构图

4.2 学习过程

在了解CNN学习过程之前，首先，要了解CNN常用的几个主要组成部分，分别为：卷积层、池化层和完全连接层。本次实验设计的CNN的向前传播如下：

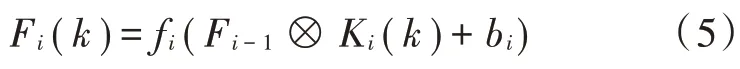
式中，若第i层为卷积层，“学习”的过程则是将上一次卷积层或者是池化层输出的特征图Fi-1（若i=1，则Fi-1表示输入图像），与当前卷积层里的核Ki(k)进行卷积，再加上偏离数列bi。最后，将此结果代入当前卷积层的激励函数fi中，得到第i层的第k个输出特征图Fi(k)。而当第i层为池化层时，对上一层特征图的处理如下：

式中Hi(k)为第i层的第k个池化层核。因为本次实验采用的池化层为平均池化层，故其核为H=

完全连接层一般都处于整个CNN结构的末尾（一般是不少于一层），不同于卷积层与池化层，它输出的不是二维的特征图而是一维的数列，对于上一层的输出结果（二维或者一维都有可能）处理如下：

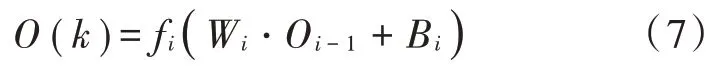
式中，W和B分别为完全连接层的权重系数和偏离数列，它们都是与第i层节点数和上一层的输出维度相关的随机数。

5 实验结果与分析

5.1 基于标准数据库的实验结果

本次实验的数据库来自于专门用于语音研究的标准数据库，要识别的语音内容为从“zero”到“nine”的单词发音。选取的数据库是来自4位男性和4位女性的320个录音（持续时间都为1 s），每个人的声音特点，包括口音、声音大小以及说话开始和结束时间等，都不一样。在训练神经网络时，语音数据中的训练数据（Training Data）分配有280个，每个单词分配28个语音，每个人的录音涵盖有3~4个；测试数据（Testing Data）40个，每个单词分配4个语音，由于随机抽取，每个人的录音涵盖有0~2个。经过采用的几种特征几何改进方法后，几种情况的二维特征所取得的语音识别效果如表1所示，每种特征都经过CNN独立训练10次得到平均值和方差，以说明其识别的正确率及其鲁棒性。由表1可知，对于未经任何几何改进的初始特征，CNN的识别正确率非常低，而且方差很大，稳定性不高。双线性插值特征，相较于初始特征，特征图尺寸增大，而非零特征区域仍处于边缘位置，正确率和方差都有所改善，但仍未到达理想的标准。在同样的尺寸下，64×64的零值填充特征却达到了比较理想的效果，而48×48的零值填充特征则正确率稍弱，但仍大大优于双线性插值特征，这样的优劣对比也证明了非零特征区域越远离边缘，训练的效果则越好。

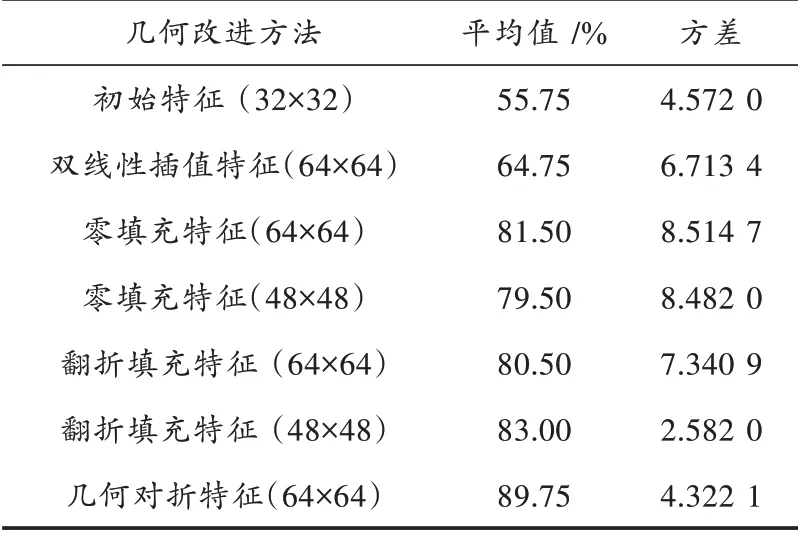
表1 CNN检测正确率

对于翻折特征和几何对折特征，可以放在一块进行说明，几何对折特征取得了所有情况中最好的效果。而不同于零填充的情况，48×48的翻折特征比64×64的翻折特征效果更好，其原因也在于，64×64的不完整特征部分更多，对CNN的识别造成了更多的干扰。

6 结 论

本文提出的基于CNN边缘化分析所采取的对二维语音特征的几何改进，在不改进CNN结构与不增加数据量的前提下，有效地改善了CNN的语音识别正确率。通过由专门用于语音研究的公共数据库[17]上的结果表明，经过不同几何改进的二维特征，相较于存在边缘影响的初始特征，其在CNN的识别效果都有了不同程度的改进。希望在未来，该类改进方法可以运用到更多种类信号，例如EEG、心电图等信号在CNN中识别效果的改进。