浅谈数学期望在经济问题中的应用
傅桂清
[摘 要] 数学期望又称均值,是概率论中的一个重要概念。随着社会经济的迅速发展,竞争越来越明显,企业所面临的经济问题也越来越多,许多实际经济问题可以通过数学期望的应用来解决。对经济问题决策的作用进一步分析,提出数学期望可以提高经济问题解决的效率,促进经济问题解决的科学性,解析了数学期望在经济生活若干问题中的运用。
[关 键 词] 随机变量;数学期望;经济问题;利润最大
[中图分类号] O211.67 [文献标志码] A [文章编号] 2096-0603(2021)39-0154-02
一、数学期望
数学期望又称均值,是概率论中的一个概念。数学期望通过研究随机变量取值反映出的平均水平,对事物的数量关系进行分析来掌握事物的变化规律。
随着社会经济的迅速发展,竞争越来越明显,企业所面临的经济问题也越来越多。为了能够在这残酷的竞争中屹立不倒,并能同时获取较高收益,企业就必须降低风险,降低成本,减少损失,那么决策者们就需要采用科学的方法来做出正确的经济决策,解决经济问题。但是现实的经济社会除了受到外部因素和决策者们主观因素的影响外,还包含很多不确定性因素的影响。所以,就需要通过数学期望来综合分析这些因素,从中选取较为合理的解决方案。
二、数学期望在经济问题决策中的作用
(一)数学期望对提高经济问题解决的效率有促进作用
企业决策者在企业运营的过程中将会面对很多复杂的问题,需要决策者对企业的经营情况和在行业所处的情况进行了解和把握,这不仅需要耗费大量的时间,还需要管理者投入较多的精力去思考和判断,这就使在一些决策确定后已经耽误了市场先机,使企业陷入被动。
那么企业在面临决策的时候就可以将数学期望的计算方法应用到里面,同时借助计算机的辅助工具快速地得到有效的结果,进而有利于企业管理者确定方案,极大地提高了决策的效率。
(二)数学期望为经济问题解决的科学性提供理论依据
知识来源于生活,是人们在生活中科学认识事物规律的总结。知识从生活中来,又离不开生活。把知识运用在生活中,还可以对客观的世界改造产生影响。对于数学学科来说,其最大的价值就是运用事物的规律来帮助人们提高实践活动的科学性。
在现实生活中,企業管理者常常是在感性思考和分析的基础上做出决策,这就使一些决策在执行的时候往往出现很多不合理性,由此导致决策失误,影响企业的正常运营,而将数学期望的方法引入决策的过程中,则可以使企业管理者基于严谨的数学运算基础上,得出科学、准确的结果,进而依据计算结果做出相应的决策,实现了科学决策、理性决策。
三、数学期望在经济问题中的应用举例
物质的进展过程以及呈现的信息通常会由于随机因素的影响,使对经济问题做出的决策带有风险性。因此,在现实问题中人们常把数学期望运用到问题决策中,通过数学期望值来判断,尽快明确决策的方案,降低存在的风险。随机变量的数学期望体现的是随机变量取值的平均水平,所以我们可以根据它具备的这一表现,利用数学期望求出各种随机因素的影响程度, 分析各随机因素重要的数字特征。下面举几个例子来说明。
(一)求职决策问题
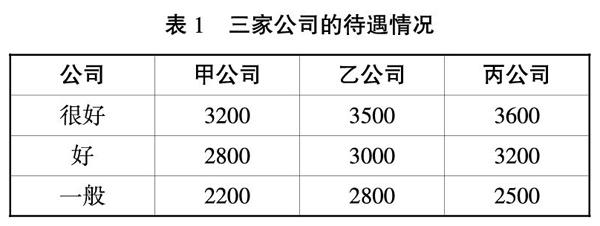
例1.设有一学生A同时收到了三个公司的面试结果,按照面试的时间顺序可以划分为甲公司、乙公司、丙公司。假定这三个公司各自招聘三种不同的职位:很好、好和一般。这位学生能获得相应职位的概率为0.1、0.2、0.5,但是这位学生A被拒绝的概率为0.2,根据要求,在面试后公司和面试者是否要接受或拒绝,都要立即做出回应,遇到这样的问题,你能给学生A提供什么建议?
分析:按照面试的时间顺序来看, 甲公司最先开始面试,那么这位学生A在面试甲公司时一定会考虑乙公司和丙公司的机会和待遇。以此类推,在选择面试乙公司时肯定也会考虑丙公司的机会和待遇。根据三个公司提供的机会和待遇进行比较,最后选择效益最大化的一家公司,我们的方案是采取期望受益最大的原则。
解:首先,从接受第三次面试的期望值来看:丙公司待遇的期望值。乙公司一般职位待遇是2800元,好的职位待遇是3000元,很好的职位待遇是3500元。同时根据第二面试的期望值来看:乙公司待遇的期望值,接受第三次面试的期望工资是3600×0.1+3200×0.2+2500×0.5=2250元,所以经过比较以及期望受益最大的原则,学生A更有可能选择乙公司,如果都被前两家公司拒绝,才会选择丙公司的面试。
在最后考虑甲公司时,只有得到很好的职位和好的职位,学生A才会接受。
根据上面的分析,我给学生A关于三次面试采取的决策提的建议:甲公司如果能提供很好的职位和好的职位,就直接在甲公司工作,不然的话就参加乙公司的面试;如果通过乙公司面试,提供的任一职位都是可以的。如果被乙公司拒绝,才接受丙公司的面试。所以,当我们在求职过程中获得多份面试时,应该进行机会和待遇的衡量比较,同时采取效益期望最大化原则,使决策的满意度和期望值得到提高。
(二)资金投资问题
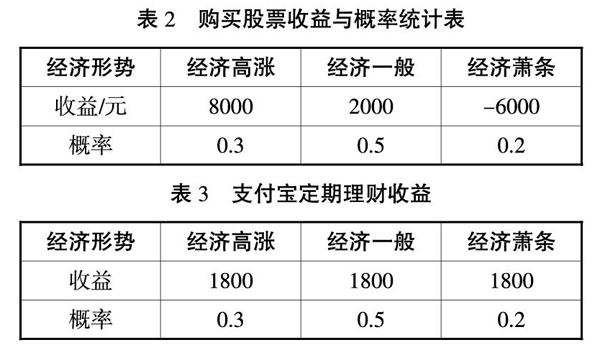
例2.某投资者有3万元闲置资金,目前有一种投资方案是支付宝里的定期理财,另一种投资方案是股票投资。若支付宝定期理财年利率为6%,到期可获得1800元;若选择购买股票,收益主要受经济发展形势影响,发展形势可分为三种状态:经济高涨、经济一般、经济萧条。那么经济高涨能获利8000元;经济一般能获利2000元;经济萧条将要损失6000元。设年经济高涨、经济一般、经济萧条的概率分别为30%、50%和20%。那么该投资者应该怎么做出选择来获得较大的收益?
分析:因为购买股票的收益受经济发展形势的影响,存入支付宝的定期理财收益与经济发展形势无关,要选择哪一种方案进行投资,就要通过计算这两种投资方案所能得到的收益期望值来进行判断。
解:依题意得下表,在不同的经济发展形势下两种投资方式一年能得到的收益与概率。
根据表格数据可以初步得到,如果购买股票在经济高涨和经济一般的情况下是合算的,但是如果经济萧条,采取存入支付宝定期理财会比较好。
购买股票收益的期望值E1=8000×0.3+2000×0.5+(-6000)×0.2=2200(元)
支付宝定期理财收益的期望值E2=1800×0.3+1800×0.5+1800×0.2=1800(元)
因此,应选择购买股票。根据收益期望最大原则,购买股票的收益比存入支付宝的收益大。但是,这种做法存在风险,期望收益最大原则是风险决策中确定投资方案的,所以,求得期望收益只是作为参考依据。
知识源于生活,又回归到生活中去。数学期望能提高经济问题解决的效率并增强经济问题解决的科学性。同时,通过本文希望学生对数学能有更深层次的了解,希望学生能更加热爱数学,投入更多的热情在数学学习和研究中。当然,需要注意的是,通过数学期望的方法来求得的期望结果可以作为企业决策者进行决策的一项参考依据,在实际的经济活动中,企业决策者仍需综合考虑市场竞争、政策变化等多种因素的影响。
参考文献:
[1]廖飞,李楠.数学期望的应用[J].牡丹江师范学院学报(自然科学版),2007(4):63-64.
[2]贺慧,李慧敏.数学期望及其在经济决策中的应用[J].科技与生活,2010(17):112.
[3]崔连香.试论数学方法在经济学中的运用[J].数理化学习(教育理论),2012(6):65-67.
编辑 栗国花

