推理公式法在青海省应用的误差分析

魏国晋 何灼伦 王统旭 刘得俊 王淑芝

摘 要：推理公式法广泛应用于水文资料缺乏地区小河流的设计洪水计算。阐述推理公式法在青海省的发展与应用，分析其计算的误差来源和处理措施，并以民和县隆治沟河段设计洪峰流量计算为例，利用《青海省水文手册》中的研究成果进行计算，得出隆治沟河段百年一遇的设计洪峰流量为531 m3/s，并与其他计算方法所得结果和已有成果进行比较，其精度符合隆治沟河段下垫面特性和产汇流特性。

关键词：推理公式法;应用;误差来源;误差控制;青海省

中图分类号：TV62;TV882.1

文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.09.009

引用格式：魏国晋，何灼伦，王统旭，等.推理公式法在青海省应用的误差分析[J].人民黄河，2021，43（9）：48-51，78.

Application and Error Analysis of Hydrological Reasoning Formula Method in Qinghai Province

WEI Guojin1， HE Zhuolun1， WANG Tongxu1， LIU Dejun2， WANG Shuzhi1

（1.Hydrology and Water Resources Prediction Center of Qinghai Province， Xining 810008， China;

2.Qinghai Water Resources and Hydropower Research Institute Co.， Ltd.， Xining 810008， China）

Abstract： Hydrological reasoning formula method is widely used in the design of the hydrological data lack of regional small rivers flood calculation. This paper expounded the hydrological reasoning model in the development and application of Qinghai Province and analyzed the calculation error sources and treatment measures. Taking the calculation of designed flood peak discharge of Longzhi Ditch in Minhe County as an example， it used the research results of the Qinghai Provincial Hydrological Manual and drew the designed flood peak discharge of 531 m3/s for once in a century. Comparing with the results calculated by other methods and the current research results， the precision conformed with the underlying surface and runoff characteristics.

Key words： reasoning formula method; application; error source; error control; Qinghai Province

水文计算中的推理公式法又称为合理化公式法，已有100多a的历史，经应用发展出现了不同形式的计算公式[1-9]。青海省水利部门从20世纪50年代开始开展水文推理公式的分析研究工作，1958年前后组织编印了《青海省水文手册》和《青海省算水账手册》等，1974年将分析资料序列增加至1970年重新修编了《青海省水文手冊》，1983年组织编制了《青海省东部地区暴雨洪水图集》（旧版）;2018年联合中国科学院地理科学与资源研究所等单位，并邀请全国10余位专家、学者，在原有科研成果和新方法研究的基础上修编了《青海省水文手册》（新版）。笔者基于新版中的推理公式法进行论证、分析、计算和经验总结，以期为青海省小流域水文计算提供参考并提高计算精度。

1 水文推理公式原理及计算方法

1.1 基本原理及公式

目前，我国水利部门使用较多的水文推理公式是原中国水利水电科学研究院提出的推理公式，属于半经验半推理的概念性模型。此模型是一定概化条件下的产物，而不是真实的物理过程。基于两种假设：一是假定由暴雨形成洪水在全流域一致（平均）;二是假定汇流面积的增长为直线变化，即产流面积与产流时间比值等于汇流面积与汇流时间比值。

推理公式的基本形式为

QP=0.278aiF=0.278aSPτnF

当τ≤tC时，洪峰流量为流域全面汇流，计算公式为

QP=0.278hττFSP

当τ>tC时，洪峰流量为流域部分汇流，计算公式为

QP=0.278htCτF

其中

htC=HP（tC）-μtC

τ=0.278LmJ1/3Q1/4P

式中：QP为设计洪峰流量，m3/s;a为洪峰径流系数;i为最大平均降雨强度，mm/h;SP为设计频率为P的雨力或最大1 h降雨强度，mm/h;P为设计频率;τ、tC为汇流、产流时间;n为暴雨递减指数;

htC、hτ为流域产流、汇流时间内的净雨深，mm;F为控制断面集水面积，km2;L为自分水岭沿主河道至控制断面的流程，km;J为沿L的加权平均比降，‰;HP（tC）为tC时间内设计频率为P的设计降雨量，mm;μ为产流历时内地面平均入渗率，mm/h;m为汇流系数;0.278为单位换算系数。

1.2 计算参数的确定

整个洪峰流量计算过程由設计暴雨、产流和汇流计算3个部分组成，主要涉及7个参数，即流域几何特征参数F、J、L，暴雨参数SP、n，产流参数μ，汇流参数m。由于参数计算的准确性是保证计算精度的关键，因此参数应因地制宜地合理选用。

1.2.1 流域几何特征参数

采用1∶50 000或1∶100 000地形图，用求积仪测量出控制断面以上的流域面积，用尺规量出河段长。近年来随着大比例尺矢量电子图层的推广应用，以及卫星影像资料精度的提高，也可利用ArcGIS等软件工具量出控制断面以上的流域面积、河长。面积、河长两次量算结果误差应控制在3‰以内，取误差范围内的两次测量结果的平均值作为计算值。比降应从河源开始逐段测量计算求得或采用调查河段实测比降代替。

1.2.2 设计暴雨参数

设计暴雨计算内容包括设计点暴雨量、设计面暴雨量、设计暴雨时深关系、设计暴雨量时程分配等[2-3，9]。无资料地区主要利用《青海省水文手册》查算出不同时段的暴雨量均值、变差系数CV、倍比系数CS/CV等进行频率计算，有实测资料地区采用实测资料进行频率计算，分别求得设计点雨量。然后，利用点面系数换算得到设计面暴雨量，采用多元回归法或线性双对数法求得各暴雨参数，并利用暴雨公式计算出相应的设计面暴雨量。

暴雨计算公式如下：

HPtC=SPtC1-n

旧版的暴雨递减指数计算公式为

n=0.045L0.984

新版的暴雨递减指数计算公式为

n=nStλC-1λlntC   （0<λ≤0.12）

式中：n、nS分别为双对数设计暴雨时深关系线的斜率及tC=1 h时的斜率;λ为经验参数，反映非线性曲线的弯曲程度。

实际计算过程中，λ的取值对n值及后续的产流参数计算有一定影响，根据青海东部地区部分水文站分析，λ值一般较小，当λ取值为零时，为线性对数关系，即n=nS。考虑到地区的差异性，旧版中n值一般采用双对数线性法计算确定。

1.2.3 产流参数

产流计算是利用暴雨推求径流（净雨）。旧版是直接建立暴雨—径流关系或采用扣损法求得径流量，对于产流时间内的平均损失率，采用平割法和交割法确定;新版采用水文模型法直接求得净雨深，以双曲线正切模型为基础，引入主雨量、主雨历时、最大可能损失等反映干旱区雨强特征与损失变化的量，具有结构简单、参数少、易识别的特点。

旧版的计算公式如下：

μ=μ0tC-athHP（tC）D

式中：μ0为产流历时tC内流域最大可能损失率;D、a为计算概化参数。

新版的计算公式如下：

RP=HP（tZ）-F（tZ）thHP（tZ）F（tZ）

F（tZ）=Sr（1-B0）tZ0.5+2KstZ

其中

Sr=89.20ζ2-62.32ζ+27.15

Ks=15.62ζ2-6.34ζ+1.69

B0=1.30η+0.81

式中：RP为设计净雨深，mm;HP（tZ）为主雨历时的设计面雨量，mm;tZ为主雨历时，h;Sr为充分风干流域土壤的吸收率，mm/h1/2;Ks为饱和流域土壤导水率，mm/h;B0为暴雨来临前流域包气带的持水度;ζ为灌木林地百分比;η为砂岩比。

一般情况下，有资料地区Sr、Ks、B0尽量利用公式计算求得，合理选值ζ、η;无资料地区也可查水文手册获得，但结果较有资料地区的计算误差稍大。

1.2.4 汇流参数

汇流计算关键是确定汇流系数m，该系数反映河槽和山坡糙率、河槽形状系数，对洪峰流量计算影响较大。无资料地区可通过查算《青海省水文手册》中的汇流参数m值表获得，也可采用经验公式计算求得，在实际应用中多采用经验公式计算。

旧版的m值经验公式如下：

m=0.75θ0.487

新版的经验公式主要采取地区水文站综合法求得，重点对区内各站点汇流参数进行归因分析，利用回归公式法求汇流系数。回归经验公式如下：

m=0.037X1+0.002X2

式中：θ为流域几何因素;X1为百年一遇最大1 h降雨量，mm;X2为流域特征系数。

2 误差来源与处理

2.1 误差来源分析

已有研究成果对误差成因均有论述，此处不再细述[10-13]。在实际计算过程中，利用不同版本《青海省水文手册》进行计算时其误差来源各不相同，主要表现在如下方面：①1974年版《青海省水文手册》采用1970年之前的资料进行分析，站点少、资料序列受限，所得成果难以准确反映时空水文变化规律;②旧版在原基础上增加了水文资料，但是分析侧重于方便和实用，其参数多为地区面上的概化值，对局部河流代表性不足;③新版充分考虑旧版存在的不足，资料序列延长至2015年，资料序列长度均超过了40 a，站点数量相对增加且布设合理，另外综合了地区各类（如气象、森林、植被等）科研成果，建立了符合青海特点的水文模型，同时汇集了国内外最新的水文理论，计算结果更接近地区实际情况，精度相对较高，但缺点同样明显，由于考虑因素较多，各指标只给了范围值而无量化值，因此实际计算过程中部分指标不易获得;④计算人员理解上的偏差造成部分参数查表查图取值和经验系数取值与实际不符，从而造成计算的误差。

2.2 误差控制

（1）设计暴雨方面。应根据计算流域所处地理位置，综合考虑降雨成因，并结合实地走访了解暴雨过程，综合评估暴雨过程及前期降雨情况。同时，利用实测资料计算时应及时补充新的水文气象资料，特别是极值，并保证极值的正确性。走访调查情况应与实地对照，或用附近中小河流雨量站监测资料进行验证，但验证时也需客观考虑青海气候的小尺度变化规律。

（2）产流计算方面。应充分了解地区产汇流参数的特性及土壤、植被组成和降水情况等，复杂区应分区計算后再根据流域权重系数或等值线法计算出整个流域产流量。同时，为提高调查精度，应利用无人机航拍和卫星技术获取不同时期影像资料，充分考虑地区间下垫面的差异性和经济发展等，综合考虑流域当前情况（如地区耕地、经济发展、草原治理修复等）合理确定土壤参数。另外，也要客观考虑突发因素的扰动影响。

（3）计算质量控制方面。应做好计算参数与邻近水文站和相似流域的比较分析，结合降雨在流域面上和垂直梯度上的变化规律，分析计算参数（暴雨折减系数、土壤吸收率、饱和流域土壤导水率等）的合理性。同时，做好与其他方法计算结果和已有成果的比较，充分考虑不同方法的优缺点，合理评判计算精度。

3 实例计算与分析

3.1 河流基本情况

2017年青海省东部民和县的隆治沟总堡乡发生大洪水，符合水文推理公式计算特性。本次计算总堡乡以上集水面积为139 km2，河道坡降为17.5‰，河道长度为19.0 km。区内气候属高原半干旱大陆性气候，具有气候时空分布差异大、垂直变化明显、降水量随海拔增高而递增等特点。区内水汽来源较充沛，是全省暴雨频次最多、强度最大的地区之一。暴雨主要发生在6—9月，尤以7—8月最多，且较大暴雨大部分是傍晚或夜间发生。洪水发生时间与降雨发生时间基本一致，多由上游大面积持续强降雨形成，洪水过程具有陡涨陡落、洪峰高、历时短、含沙量大等特点。暴雨集中程度较高，部分地区植被不佳，洪水期水土流失严重，河流含沙量较高。

3.2 计算成果

3.2.1 设计暴雨计算

（1）点面暴雨计算。设计断面以上区域没有实测水文资料，也没有长序列的实测雨量资料，因此分别利用新版、旧版进行计算。设计点面雨量成果见表1、表2，双对数关系曲线见图1，设计暴雨时深关系见图2。

（2）设计雨量时程分配。计算流域位于湟水谷地浅山脑山混合区，是青海省东部固定暴雨中心。本次采用青海省东部地区设计暴雨雨型“模板”——浅山脑山区1 h主雨峰对齐雨型过程[6]进行分配。新旧版的雨量时程分配见表3、表4。

3.2.2 产流计算

相关参数根据隆治沟所处地理位置及其参考范围合理取值，按旧版公式计算得出

htC=16.0 mm，μ=29.3 mm。新版洪水只考虑造洪雨期（主雨期），按瞬时雨强≥2.5 mm/h的降水作为主雨，采用暴雨公式分别计算主雨量和主雨历时，综合计算确定R1%=31.9 mm、μ=13.1 mm。

3.2.3 汇流计算

汇流时间和洪峰流量一般采用图解法、试算法和数值法确定，本次采用试算法进行计算。首先按全面汇流公式计算QP，再将各参数代入汇流时间计算公式反算出τ，验算是否τ≤tC。若τ≤tC，则按全流域汇流公式计算;若τ>tC，则按部分流域汇流公式计算。旧版汇流参数m值经查图确定为3.50，计算河流为部分汇流，τ=1.21 h，洪峰流量Q1%=504 m3/s。新版汇流参数m值综合计算确定为1.80，计算河流为部分汇流，τ=2.36 h，洪峰流量Q1%=531 m3/s。

3.2.4 合理性分析

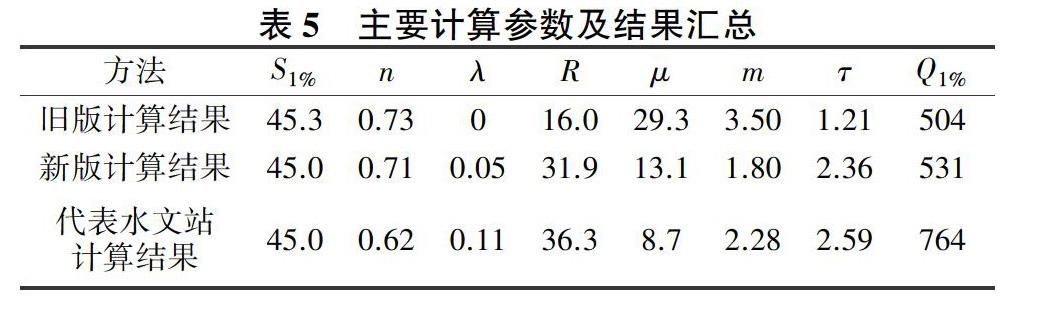
从表5可知，旧版计算的设计面雨量、暴雨递减指数基本接近，净雨深、平均损失率、汇流参数等相差较大;洪峰流量计算结果上两者基本接近，偏差在5%以内。与邻近水文站进行比较，新版计算主要参数更为接近，认为更为合理，原因是在计算过程中充分考虑了地区下垫面、土壤组成情况等。

新版计算成果与其他方法计算结果进行比较，基本接近水文比拟法成果（535 m3/s），较洪峰模数等值线图法成果（311 m3/s）偏大71%。与已有成果比较，较文献[14]中采用成果665 m3/s偏小25%，较文献[15]中采用成果545 m3/s偏小3%。综上所述，此次采用新版的水文推理公式计算成果较为合理。

4 结 语

水文推理公式法利用《青海省水文手册》进行计算是常用捷径，也是提高计算精度的重要保障。应用

过程中大部分河流的计算精度相对较高，但少数河流的计算结果与实际情况有较大差异，这是不可避免的。造成这种情况，一方面是这种方法自身的缺陷所致，另一方面是青海高原地区的复杂性所致。综上所述，计算时应结合地区实际情况合理确定方法，同时做好计算精度控制。今后仍需加强方法自身的研究，做好资料序列的延长分析和地区监测站点的规划布设，以及拓展资料的积累，如森林、植被、草原、耕地等已有研究成果，以确保水文手册的可操作性。

参考文献：

[1] 陈家琦.推理公式法的发展及其综述[J].北京：中国工业出版社，1966：5-7.

[2] 青海省水利电力局水文总站.青海省水文手册[R].西宁：青海省水利电力局水文总站，1974：10-17.

[3] 青海省水利厅水文总站.青海省东部地区暴雨洪水图集[R].西宁：青海省水利厅水文总站，1983：1-12.

[4] 陈家琦，张恭肃.推理公式的应用与改进[J].水文，1983，3（1）：2-9.

[5] 刘权授，胡凤彬.谈推理公式的改进：读“推理公式的应用与改进”一文后[J].水文，1984，4（3）：51-54.

[6] 陈家琦，张恭肃.小流域暴雨洪水计算[M].北京：水利电力出版社，1985：1-92.

[7] 刘光文，叶守泽.水文水利计算[M].北京：水利电力出版社，1994：97-115.

[8] 王国安，贺顺德，李荣容，等.论推理公式的基本原理和适用条件[J].人民黄河，2010，32（12）：1-4

[9] 李其江.青海省水文手册[M].西宁：青海省人民出版社，2018：22-30.

[10] 唐洪波，何灼伦，王霖.格库铁路青海境内无资料地区设计洪峰流量计算分析[J].宁夏大学学报（自然科学版），2020，41（1）：92-97.

[11] 肖雪庭.水文计算中推理公式的应用及参数的分析[J].有色矿山，1997，26（1）：40-43.

[12] 辛波.改进的推理公式法在无资料地区山洪评价计算中的应用[J].水利技术监督，2018（2）：77-79，181.

[13] 高鹏杰.应用推理公式计算洪水中的不足与改进[J].北京水利，1997（5）：15-17.

[14] 青海河海水利水电设计有限公司.青海省民和县隆治沟夏家河—哈家村段防洪治理工程初步设计报告[R].西宁：青海河海水利水电设计有限公司，2016：95-100.

[15] 青海省水文水资源勘测局.青海省民和县隆治沟、杏儿沟、大马家沟2018年洪痕断面测量及分析计算报告[R].西宁：青海省水文水资源勘测局，2017：87-101.

【责任编辑 张 帅】