浅海内波环境下声场时间相关特性∗
胡 平 彭朝晖 李整林
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
声场的时空相关特性是声学研究的一个重要方向,认识和利用声信号的时空相关性对于水下目标探测、通信等设备的研制及应用有重要意义。内波的分布范围相当广泛,在世界各大洋和边缘海域都有内波存在[1]。内波在海洋中的传播会引起水声信道特征随时间的变化,从而导致声信号的时间相关性变差。内波引起声场时间相关性的相关研究也是当今的热点问题。
Yoo 等[2]利用SWARM95 实验水文环境,数值仿真了存在内波时的匹配场时间相关。Huang等[3]在ASIAEX2001东中国海实验水文环境下,仿真了内波对声场时间相关的影响,对比实验结果解释了引起时间相关下降的原因是同时存在线性内波和孤立子内波。李整林等[4−5]研究表明内波的存在降低了匹配场的定位性能。Yoo[6]利用SWARM95 水文数据,通过数值仿真研究了浅海内波环境下宽带信号的时间相关半径与声源中心频率、声源-接收距离的关系,结果表明与深海情况一致。Yang[7−8]对4 次实验数据(ADVENT99、ASCOT01、SWARM95、RAG03)进行分析,得到了信号相干时间与声源频率和收发距离的关系,结果表明相干时间与声源频率的−3/2 次方成正比,与收发距离的−1/2 次方成正比。季桂花[9]利用1996年中美远黄海实验和ASIAEX2001 南中国海实验数据进行数值仿真分析,发现存在线性内波的两种浅海水文条件下匹配场时间相关长度与内波引起的声速标准差之间的关系相近。任云利用ASIAEX2001 南中国海实验和2009年6月南中国海实验的水文数据,研究了浅海中孤立子内波对声场时间相关性的影响,结果表明声传播路径上大振幅非线性内波是导致声场时间相关半径下降的重要原因,并拟合了声场时间相关半径与声速标准差、收发距离的关系式[10]。张海青[11]通过对AEYFI+05黄海实验数据处理分析,发现1 号简正波的传播时间起伏谱可反映M2 潮变化,另外对实验数据处理发现某时段个别水听器有强起伏,并用理论解释了实验现象。于彬等[12]通过对ASIAEX2001 数据处理以及数值仿真,研究了声源深度对声场时间相关的影响,当有强孤立子内波经过传播路径时,声源深度越深,匹配场时间相关半径越大。马树青[13]研究分析了内波环境下声源位置对于传播损失的影响,还发现孤立子内波经过声源时会发生较规律的起伏,并用三维模型研究了孤立子内波对水平阵波束形成的影响。
综上所述,浅海中内波的存在会极大地影响声场的时间相关半径。中国科学院声学研究所的相关工作人员于2015年在南中国海北部海域开展了为期4 天的定点收发起伏实验,获得了宝贵的实验数据,针对此次实验数据,通过统计方法研究线性内波与孤立子内波期间声场时间相关半径的统计特性,同时拟合线性内波期间声场时间相关半径与声速标准差关系式。
1 南中国海北部海域声传播起伏实验
1.1 实验介绍
南中国海是内波频发的海域,实验海域位于东沙群岛西南方向,整体海深变化很小,平均海深约109 m,实验期间海况良好。
如图1所示,实验中有3 个固定仪器布放站点。S1点海深为111 m,布放了发射潜标和温度链;O1点海深为105 m,布放了接收潜标和温度链,S1与O1间隔14.8 km;H1点海深为105 m,布放了温度链,分别与S1、O1点间隔14.4 km、6.5 km。声源为线性调频信号,中心频率200 Hz,带宽50 Hz,声源级178 dB,放置深度108 m,每3 min 发射1 组信号,每组包含两个线性调频信号,脉冲宽度10 s,间隔30 s。接收端为16 阵元垂直阵,16 个水听器分布在水深21~78 m的范围内。
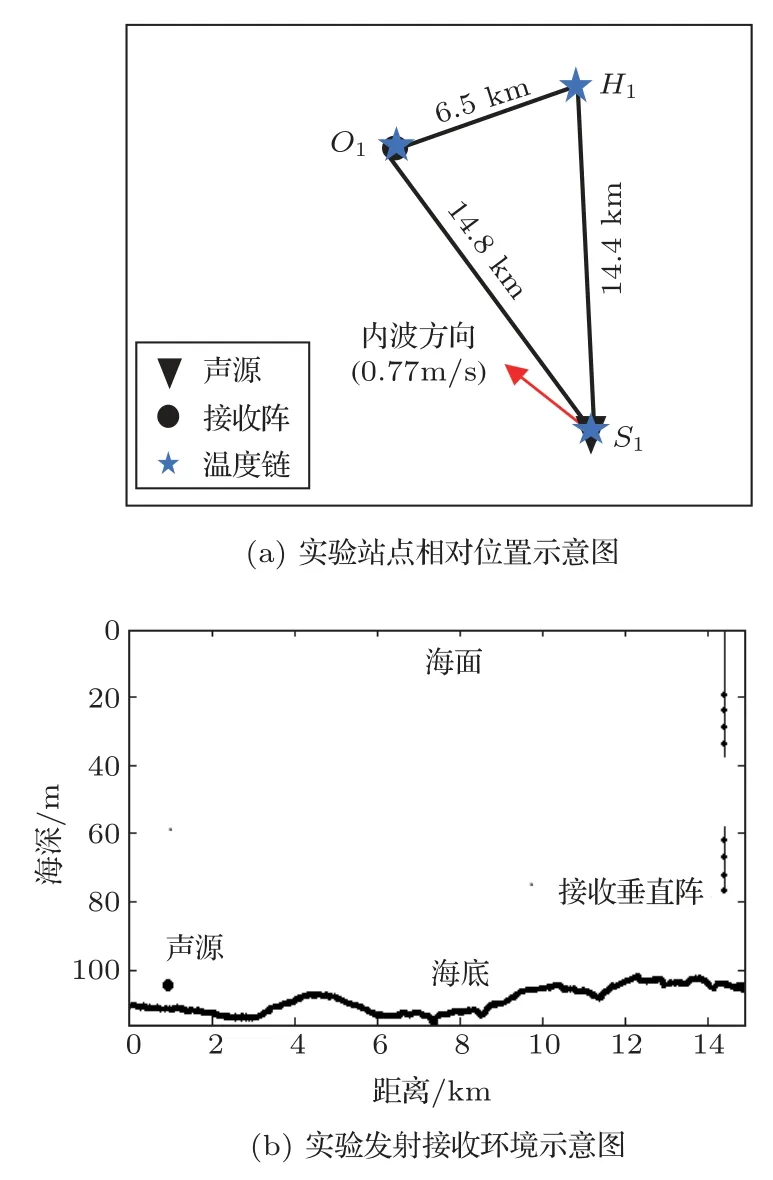
图1 实验设备布防与收发环境示意图Fig.1 The locations of instrument deployed and experimental launch-reception environment
图2 给出了试验期间3 个站点的温度数据,对应时间为13 11:00–14 11:00,图中从上至下依次为S1、H1以及O1点处温度链测量的温度剖面数据。图中可以看出在13 23:00 之后主要为小幅度线性内波,13 23:00 之前则存在大振幅的孤立子内波。对比3 条温度链数据,可看出此大振幅孤立子内波特征相似,认为此为同一孤立子内波串依次经过S1、H1以及O1站点。由图2 中孤立子内波串的首个波包在各个站点的到达时间差及站点间相对距离,可估算得到孤立子内波在此传播路径上的方向与速度,结果为内波方向与S1O1方向夹角偏西11.17°,平均传播速度为0.77 m/s。

图2 3 个站位实测温度数据(13 11:00–14 11:00)Fig.2 Temperature profiles variation of three experiment site(11:00 on the 13th–11:00 on the 14th)
1.2 声场时间相关系数
在海洋环境中,声场随时间实时变化,用声场时间相关性来描述这一变化。即声场时间相关指的是稳定声源连续发射同一信号时,水听器接收信号在时间上的变化。用声场时间相关系数来定量表示声场时间相关性的强弱程度:
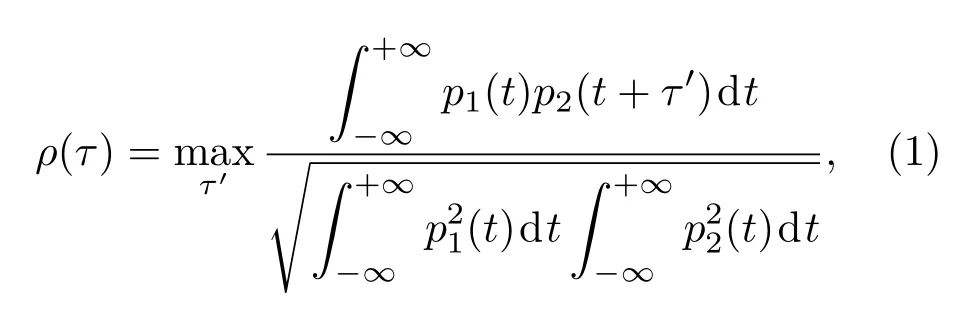
式(1)中,p1(t)和p2(t)为水听器接收到的同一声源在不同时刻发出的同一信号,τ为延迟时间,它等于右侧式子取最大值时τ′的值。
图3分别给出了孤立子内波期间以及线性内波期间某段时间的声场时间相关系数随时间的变化,图中横坐标为每个信号相对于第一个接收信号的延迟时间,纵坐标为每个信号与第一个接收信号的相关系数值,采样间隔3 min。图3 中可见声场时间相关系数随延迟时间有上下起伏波动,整体呈下降趋势。图3(a)为孤立子内波期间的一次声场时间相关系数变化图,可以看出曲线下降很快,第5个信号,也即第15 min 时,时间相关系数已经下降到0.6以下,之后的时间也基本都在0.8以下。图3(b)为线性内波期间的一次声场时间相关系数变化图,可以看出曲线下降很慢,直到第6 h,时间相关系数依然在0.6 以上,而在前4.5 h 时间相关系数也基本都在0.8 以上。说明孤立子内波的存在极大地影响了声场的时间相关特性,会使得声场时间相关系数急速下降。

图3 声场时间相关系数Fig.3 Sound field time correlation coefficient
1.3 声场时间相关半径及其统计特性
由公式(1)可知,声场时间相关系数是延迟时间τ的函数,当声场时间相关系数下降到某个值(这里取0.707)时所对应的延迟时间τ称为声场时间相关半径。这里用τ0.707来表示声场时间相关半径,则
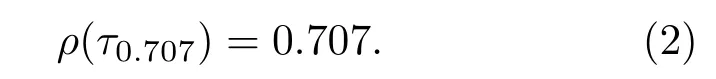
为具体研究线性内波期间以及孤立子内波期间声场时间相关半径的统计特性,选取两个时间段数据做具体分析:时间段1 对应14 3:00–7:00,期间主要为线性内波,水文环境较平稳;时间段2对应13日14:00–18:00,期间声传播路径上主要存在孤立子内波,水文环境起伏剧烈。
对两个时间段的声场时间相关半径进行概率统计,在0~300 min 范围内,划分为固定的采样区间,分别计算每个区间的概率值,即

式(3)中,τi代表第i个区间的声场时间相关半径中间值,ni为第i个区间的样本数,N为样本总数,P(τi)则为第i个区间的概率值。采样区间选择时,时间段1 线性内波期间相关半径较长,取16 min 为一个区间;时间段2 孤立子内波期间,相关半径较短,取3 min为一个区间。
图4 为上述两个时间段内,接收深度分别为22.6 m、64.6 m 处声场时间相关半径的统计概率分布柱状图,图中横坐标为声场时间相关半径,纵坐标为概率。图4 中,线性内波期间22.6 m 处声场时间相关半径约分布在0~350 min,主要集中在100~200 min,统计均值为145.4 min,标准差为71.6 min;64.6 m 处时间相关半径约分布在0~200 min,主要集中在40~100 min,统计均值为78.7 min,标准差为36.4 min。而孤立子内波期间,声场时间相关半径在22.6 m以及64.6 m处基本都小于20 min,22.7 m 处时间相关半径统计均值为7 min,标准差为4.9 min;64.6 m处时间相关半径统计均值为6.2 min,标准差为4.7 min。由以上数据可以看出:
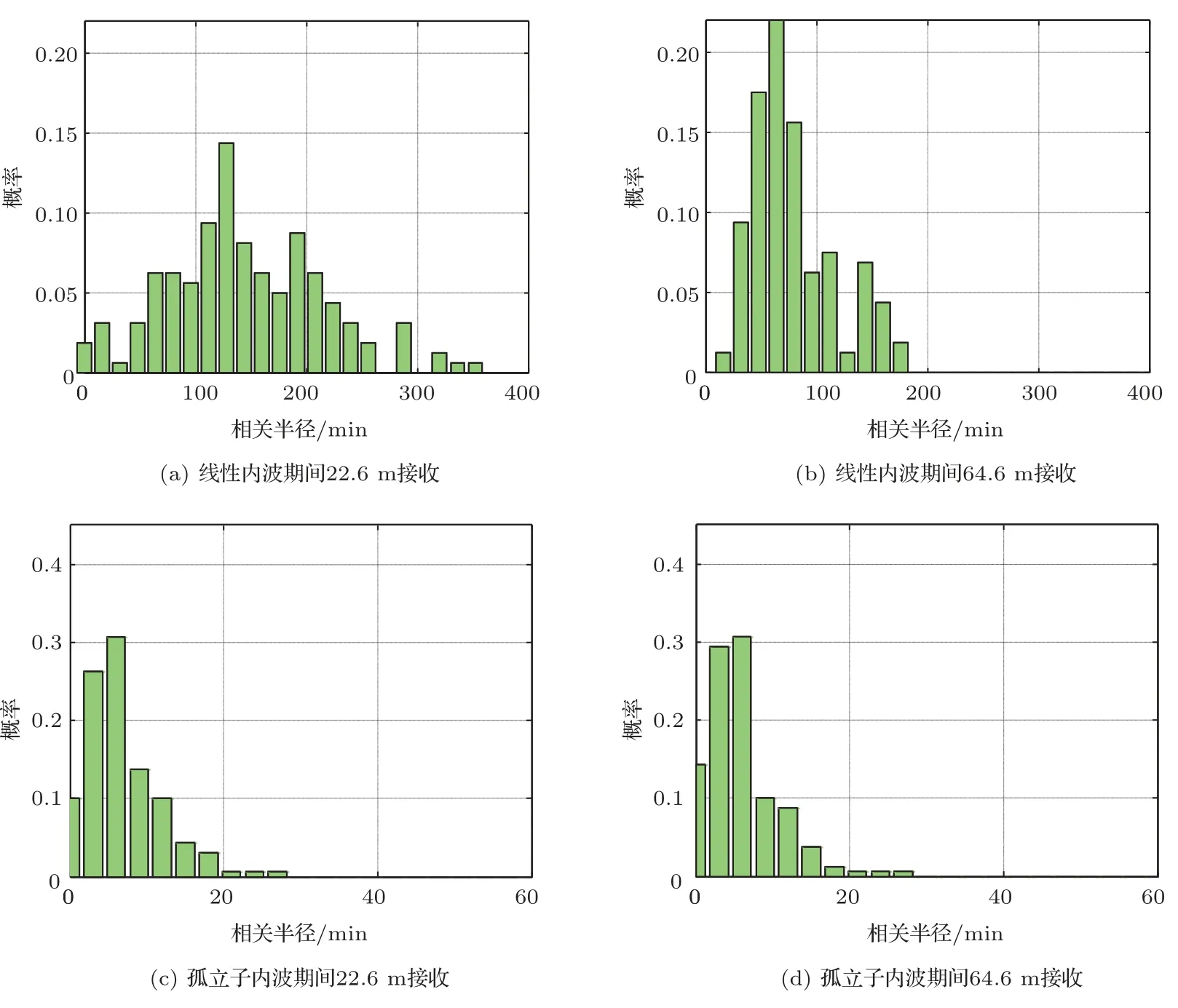
图4 声场时间相关半径实验数据统计结果Fig.4 The experimental statistics of sound field time correlation length
(1)比较不同时间段,相对于线性内波期间,孤立子内波期间的时间相关半径骤减,且分布范围较窄,标准差较小。这是由于孤立子内波期间,水文环境起伏较大,信号传播过程中受时变起伏较大的声场影响,导致各个时间段接收到的信号差异性增加,时间相关半径减小。
(2)比较不同深度处结果,在孤立子内波期间,其时间相关半径分布差异很小,分布范围基本都为0~20 min;在线性内波期间,22.6 m 处分布范围更大,其时间相关半径可在0~350 min 上下起伏,而64.6 m 处时间相关半径相对集中些,峰值点的概率值更大。这是由于在不同的深度,受水文环境的影响不同,内波影响较大的深度为温跃层深度,由于声源在108 m 处,22.6 m 深度接收相当于要穿越整个温跃层,对于现行内波期间,整体时间相关半径较大,22.6 m 处受温跃层影响较大,其统计分布范围更宽,统计标准差更大。
以上,线性内波环境下声场时间相关半径远大于孤立子内波环境,且声场时间相关半径展宽较大,分布范围广。同时,在线性内波期间64.6 m处比22.6 m处时间相关半径更集中些。
2 声场时间相关半径统计特性仿真分析
2.1 仿真环境
仿真环境计算中,考虑实验中水平变化的水文环境,采用抛物方程模型RAM[14]进行数值仿真。环境设置如图5所示,海底地形如图1(b)所示,声源深度108 m,信号频带175~225 Hz,接收距离14.8 km,垂直接收阵列覆盖了海面到海底全深度。海底底质等参数来源于同一海区海底参数反演结果[15],即海底声速1595.5 m/s,海底密度1.7 g/cm3,衰减系数0.39 dB/m。
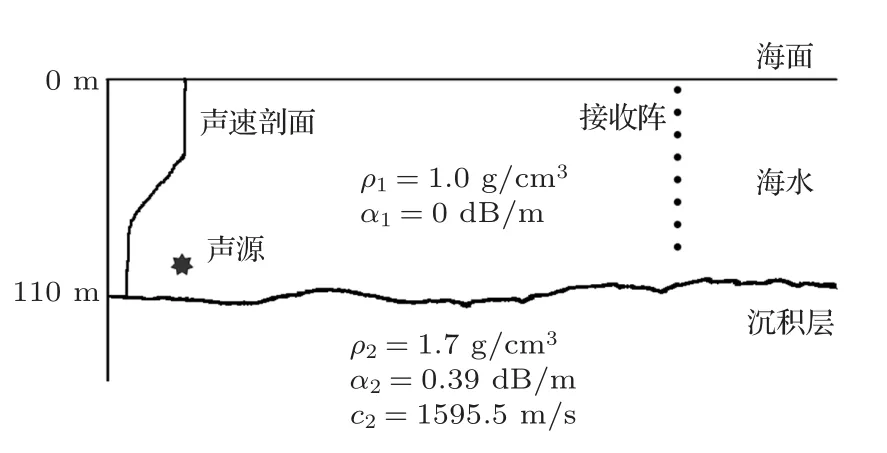
图5 声场仿真环境与参数Fig.5 Environment parameters of sound field simulation
收发距离上的声速场采用短时冻结海洋模型的方法估算,即利用温度链测量的温度剖面数据来构建动态海洋环境声速场。仿真中盐度数据以及海底与海面附近的声速来源于S1站点温盐深仪(Conductivity,temperature,depth,CTD)的测量数据。由以上温盐压数据代入海洋声速的经验公式[16]可得到此站点各时刻的声速剖面,再根据传播信道方向上孤立子内波的传播速度,将以上声速剖面转化为沿声传播路径方向随空间变化的声速场,即
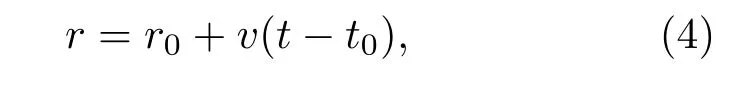
式(4)中,r0为温度链的位置(以声源O1站位为参考零点),对于O1站点的温度数据取r0=0 m处,对于S1站点的温度数据取r0= 14.8 km 处;v是声传播路径上孤立子内波的传播速度,前文已求得此次实验中v=0.77 m/s。
2.2 声场时间相关数值仿真
根据图5中仿真环境参数,利用RAM程序仿真可得到频域声信号。根据Fourier变换的性质,由式(1)可得声信号时间相关系数的频域计算公式为[17]

其中,P1(ω)、P2(ω)分别为信号p1(t)、p2(t)的频谱,[ω1,ω2]为信号的正频率的范围(实信号频谱在正负频率轴上共轭对称)。用求和的形式表示:
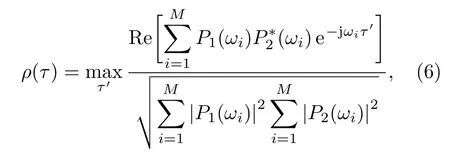
其中,i为频率序号,M为频率总点数。依然取声场时间相关系数下降0.707 时对应的延迟时间τ作为声场时间相关半径。
图6 给出了与图4 对应的声场时间相关半径的仿真统计图,其中,线性内波期间相对孤立子内波期间,声场时间相关半径取值更大,且分布范围更广;线性内波期间的不同深度处结果可以看出,22.6 m接收处声场时间相关半径分布范围更大。对比图4可以看出,以上结果与实验相符,两者的概率分布范围以及分布趋势符合良好,说明仿真效果尚可。
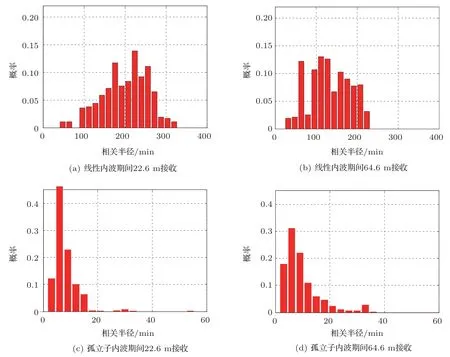
图6 声场时间相关半径数值仿真统计结果Fig.6 The simulation statistics of sound field time correlation length
3 结论
通过对2015年南中国海实验数据处理分析,在175~225 Hz的频段上,得到以下结论:
(1)大振幅孤立子内波的存在极大地降低了声场的时间相关半径,实验中浅海线性内波环境下声场时间相关半径可达到1~5 h,而孤立子内波环境下声场时间相关半径基本低于20 min。
(2)在不同深度处,孤立子内波期间声场时间相关半径分布差异不大,而线性内波期间,22.6 m处声场时间相关半径分布范围比64.6 m 处更大,标准差更大。
致谢感谢参加此次2015 南中国海声传播实验的“实验1”科学考察船和所有科考队员海上辛苦工作,为本研究提供了宝贵的实验数据。

