砂砾岩压裂中砾石对水力裂缝扩展影响机理研究

董卓鑫， 张 辉， 艾 池， 马旭昇， 李有翼， 周江浩

1中国石油大学(北京)石油工程学院 2东北石油大学石油工程学院3中国石油青海油田公司采油五厂

0 引言

砾岩是岩石碎屑经过沉积作用后形成的一种岩石，其主要由连接砂砾岩中砾石的基质和压实在砂砾岩中的砾石构成。由于其岩性致密，渗透性差，在开采砂砾岩油藏时需要大规模的水力压裂[1-2]，打开油气渗流的通道。许多学者针对砾岩的水力压裂问题做了很多研究[3-5]。在水力压裂过程中，水力裂缝与砾石相接触，影响裂缝的走向，引起水力裂缝穿过砂砾岩打开油气流动的通道，或者水力裂缝绕过砾石颗粒，与其它裂缝相交，形成缝网。因此研究水力裂缝与砾石的相互作用规律是研究砂砾岩水力压裂的关键。

孟庆民[6]通过大尺寸真三轴模拟压裂裂缝扩展实验证实了在砂砾岩储层中砾石会对水力裂缝扩展产生重要影响；XV C Z[7], YAN Y[8]在实验中观测到了裂缝遇砾石的绕砾和穿砾现象；张红静[9]、李连崇[10]等分别通过数值模拟和实验研究发现水力裂缝与砾石相遇主要会出现绕砾、穿砾和止裂三种现象,并观察到砂砾岩中水力裂缝的遇砾扩展以绕砾为主; Anderson[11]、Teufel[12]通过在界面添加润滑剂改变界面摩擦力，证实了摩擦阻力对水力裂缝在界面扩展的影响。ZHU H Y[13]、杜修力[14]将砾石与基质的结构分为“基质—交界面—砾石”结构；余东合[15]、张红静[9]针对“基质—交界面—砾石”结构砂砾岩模型进行数值模拟，发现胶结面是影响水力裂缝扩展的重要因素，模拟结果与砂砾岩压裂实验较为吻合。

针对砂砾岩的研究虽然进行了大量的压裂实验和数值模拟，取得了一定的共性认识和结论。但是这些研究都是从实验现象和模拟结果中总结得出的结论，缺乏水力裂缝遇到砾石延伸扩展的机理性研究。为此，本文基于断裂力学，建立了砂砾岩压裂水力裂缝遇砾石相互作用模型，为水力裂缝在砂砾岩中扩展方向的判别提供依据。

1 裂缝尖端微裂区特征及主应力求解

在水力压裂过程中，水力裂缝尖端会存在一个微裂区，区域内存在明显的应力集中现象,见图1。

图1 水力裂缝应力场模型

这个微裂区内不断有微裂纹生成，微裂纹不断增多最终贯通形成裂缝，微裂区引导着水力裂缝的扩展。当微裂区与砾石相遇时，水力裂缝扩展会受到砾石的影响。

为了进一步研究裂缝尖端微裂区与砾石的相互作用，建立平面应变条件下裂缝尖端微裂区分布计

算模型并计算微裂区内裂缝三向主应力。如图1所示，将天然裂缝看成一个摩擦界面，其逼近角为θ,水力裂缝延伸方向与最大主应力之间的夹角为φ,泊松比为ν，在水力裂缝和远场地应力共同作用下，Ⅰ-Ⅱ复合型裂缝的三向主应力在笛卡尔坐标系中可以表示为：

(1)

式中:r—距离裂纹端部的距离；

θ—应力场内部到裂纹端部与裂纹延伸方向之间的夹角；

φ—裂纹延伸方向与水平最大主应力延伸方向的夹角；

KⅠ和KⅡ—分别为Ⅰ型和Ⅱ型应力强度因子；

σH—最大主应力；

σh—最小主应力。

2 水力裂缝与砾石相互作用模型

水力裂缝在延伸过程中，在裂缝和地应力的共同作用下，在水力裂缝尖端会形成应力场。在应力场内形成产生微裂缝的微裂区。当砾石与微裂区接触时，砾石胶结面与水力裂缝会产生相互作用，作用结果可以归为两类：

(1)砾石胶结面发生剪切滑移。当水力裂缝微裂区与砾石胶结面相交时裂缝尖端应力场和远场地应力在胶结面的两侧产生一定的剪应力，胶结面上的剪应力足够时，砂砾岩基质与砾石胶结面会发生失稳，裂缝沿胶结面扩展。

(2)水力裂缝穿过砾石胶结面。若砾石胶结面不产生滑移，且水力裂缝对砾石破坏作用较大，会先于砾石侧形成微裂纹。水力裂缝继续扩展与微裂纹连通，最终贯穿砾石。

2.1 水力裂缝穿砾扩展模型

当裂缝微裂区与砾石接触后，砾石与水力裂缝产生相互作用，若要预测水力裂缝的扩展方向，首先应该判断水力裂缝能否穿过砾石，研究水力裂缝的穿砾情况。

最大拉应变强度准则认为，脆性断裂是由于最大拉伸线应变达到极限导致的：

σ1-υ(σ2+σ3)=σT

(2)

结合公式(1)与公式(2)，计算最大拉应变强度准则微裂区临界半径rc：

(3)

其中:

当水力裂缝与砾石胶结面接触时，由于界面两侧的岩性不同，砾石内部抗拉强度大于砂砾岩基质的抗拉强度，水力裂缝与胶结面刚接触时，其无法直接穿越砾石胶结面，压裂液涌入裂缝尖端，裂缝内压力升高，在砾石内侧产生微裂纹，水力裂缝具有了穿越砾石胶结面的能力。

若要水力裂缝穿过砾石胶结面，除了需要最大拉应变强度准则能满足其判定条件外，还需要砾石胶结面不会在地应力和裂缝应力场作用下发生剪切失稳。即满足Mohr-Coulomb准则：

|τrθ|<τ0-μσθ

(4)

式中:τ0—砾石胶结面的黏聚力，MPa；

μ—界面的摩擦系数。

Ⅰ-Ⅱ混合型裂缝尖端应力场的极坐标形式：

(5)

将式(5)代入式(4)中，可得到判定天然裂缝剪切滑移的临界条件：

(6)

当裂缝同时满足强度和不产生滑移时，水力裂缝能穿过砾石，在另一侧基质中继续扩展。

2.2 水力裂缝绕砾扩展模型

当水力裂缝无法穿砾时，其会转向沿砾石胶结面扩展。根据砾石磨圆度不同可以分为角砾与圆砾。本文分别建立两种绕砾模型分别研究水力裂缝在遇角砾与圆砾的相互作用。

如图2为水力裂缝遇角砾的绕砾模型，当水力裂缝与砾石胶结面接触，压裂液进入胶结面，可通过虚拟裂纹法判断裂缝的扩展形态。

图2 水力裂缝绕角砾模型

在裂缝转向方向上建立虚拟裂纹1及虚拟应力场x1y1，那么虚拟裂纹在砾石胶结面中产生的正应力和切应力分别为：

(7)

(8)

rc—虚拟裂纹方向水力裂缝微裂区半径。

由于水力裂缝1与原水力裂缝具有同等的强度，水力裂缝应变与虚拟裂缝应变量相同，将公式(7)、公式(8)与裂缝应力场联立可得出虚拟裂缝的应力强度因子表达式：

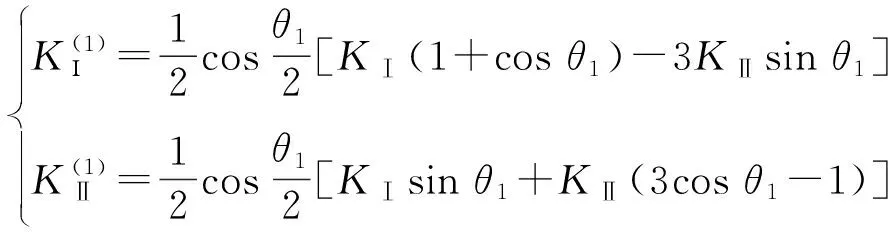
(9)

若虚拟裂缝在该方向的拉应变能达到砾石胶结面的抗拉强度，水力裂缝发生转向，沿砾石表面扩展：

(10)

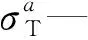
当裂缝沿砾石表面扩展至拐角，此时会发生角度为θ2的二次转向，由于砾石的阻挡，水力裂缝继续紧贴砾石扩展。同理建立虚拟裂缝2及其应力场x2y2，当其满足强度条件时，水力裂缝绕砾成功，其应力强度因子表达式为：

(11)

虚拟裂纹2沿砾石表面b扩展的临界条件为：

(12)

图3为水力裂缝在圆形砾石胶结面的扩展情况，于A点与圆砾接触，于B点离开圆砾向基质中扩展。在砾石上转过的角度为α。当第一条虚拟裂缝能够在胶结面扩展时，可以将这一段近似分解为n等份的等腰三角形，水力裂缝经过n次偏折，每一次偏折偏转α/n，偏转角减小α/n，根据虚拟裂纹法：

图3 圆形砾石水力裂缝绕圆砾模型

(13)

水力裂缝沿圆砾表面扩展的临界条件为：

(14)

对比两种砾石的转向判定条件可以发现，菱角状砾石为圆砾的一种特殊情况，随着角砾的棱数量的增多，两种砾石与水力裂缝作用结果趋于相同。

3 水力裂缝扩展模型的敏感性分析

3.1 强度准则对水力裂缝穿越砾石的影响

在纯Ⅰ型裂缝条件下，取岩石的抗拉强度σT和砾石胶结面的界面黏聚力为零，泊松比υ为0.2，水平最小主应力σh为10 MPa。选取5个逼近角β，将最大拉应变强度准则与最大拉应力强度准则进行对比，如图4所示。

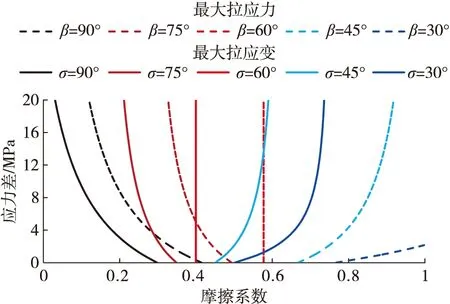
图4 最大拉应变准则与Gu准则的穿越曲线对比

在图4中，每条曲线表示在当前逼近角下水力裂缝穿过砾石胶结面的临界状态，其右侧代表水力裂缝穿过砾石在砾石中扩展，左侧代表未穿过。通过准则间的对比可以看出，两个准则在整体趋势上是一致的，但本文的准则在整体趋势上，向左侧移动，且随着逼近角的减小，这种差异越大。这是由于Gu准则并没有考虑中间主应力对砾石胶结面滑移的影响。本文准则均衡考虑了三向主应力的影响，因此水力裂缝穿过砾石胶结面的可能性增加。

3.2 水力裂缝穿砾扩展模型敏感性分析

基于表1中的参数对水力裂缝穿砾行为进行敏感性分析，分析裂缝的结果如表1所示。

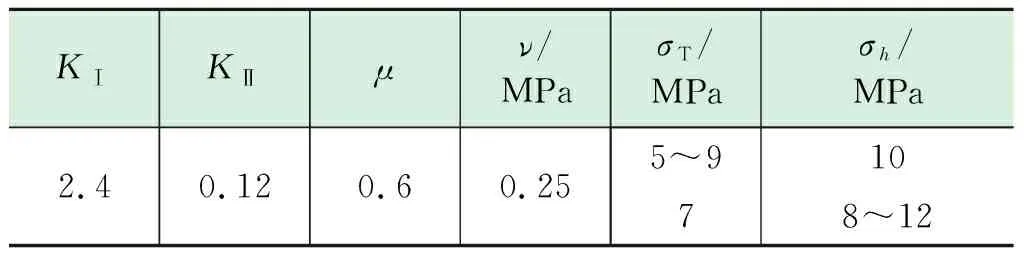
表1 水力裂缝穿砾敏感性评价基础参数表

如图5所示，在不同砾石抗拉强度下，水力裂缝与砾石相交的穿越判定曲线，随着砾石抗拉强度由5 MPa增长到9 MPa，穿越曲线大幅度向右侧移动，说明随着砾石抗拉强度的增加，水力裂缝越难穿过砾石，砾石的抗拉强度是影响水力裂缝穿越的重要因素。

图5 不同砾石抗拉强度下的穿越曲线

如图6所示，在不同最小水平主应力下，水力裂缝与砾石相交穿越判定曲线，随着最小水平主应力由8 MPa增长到12 MPa，穿越曲线逐渐向左侧移动，说明随着最小水平主应力的增加，水力裂缝越容易穿过砾石。

图6 不同最小水平主应力下的穿越曲线

从以上分析中可以看出，决定水力裂缝穿砾行为的主要是裂缝的逼近角与砾石强度，水力裂缝穿砾难度较大，其主要的扩展模式应当是沿胶结面进行转向扩展。

3.3 水力裂缝绕砾扩展模型敏感性分析

基于表2中的参数对水力裂缝绕砾进行敏感性分析，研究砾石形状对水力裂缝转向效果的影响：

表2 水力裂缝转向敏感性评价基础参数表

首先应用基本参数对水力裂缝偏转过程进行分析。如图7，水力裂缝在转向过程中，每一次的偏转都会使转向曲线下降一定距离，说明在裂缝转向过程中，水力裂缝强度逐渐降低，因此最后一条虚拟裂缝所具有的虚拟拉应变最小，可以将最后一条虚拟裂纹的拉应变来作为判断水力裂缝能否绕过砾石。

图7 水力裂缝强度随偏转次数变化曲线

如图8，由于角砾棱角数量不同，随着所需转向次数T由2次到10次，转向曲线逐渐向上移动，表征水力裂缝成功转向并扩展的面积越来越大。说明随着砾石棱角的增多，水力裂缝越容易绕过砾石。

图8 不同砾石偏转次数下水力裂缝转向判定曲线

如图9所示，当转向次数较低时，拉应变波动明显，随着转向次数的不断增加，拉应变上升幅度逐渐降低并逐渐趋于平稳，当转向次数达到200次及以上时，拉应变基本不变。实际上，随着转向次数的增加，砾石逐渐变得圆润，因此圆砾可以看作角砾的一种特殊形式。

图9 在不同角度下转向次数对虚拟拉应变的影响

4 结论

本文通过结合Mohr-Coulomb准则与设置虚拟裂缝来判断水力裂缝在砂砾岩中的延伸情况，得出了以下几条结论：

(1)水力裂缝与砾石的接触，只有在高逼近角下，高地应力差条件下发生穿砾的现象。在大多数情况下，水力裂缝无法穿过砾石。

(2)水力裂缝在单次转向过程中，随着偏转次数的增加，虚拟拉应变逐渐降低，可用转向时的虚拟裂纹强度来判断水力裂缝能否绕过砾石。

(3)水力裂缝的转向扩展与砾石的形状有关，砾石越圆，水力裂缝的绕砾越容易进行，说明圆砾比角砾更容易形成复杂缝网。