考虑跨线运行的城市轨道交通线网交路优化研究

刘 杰

（重庆工程职业技术学院 智能制造与交通学院，重庆 402260)

随着城市轨道交通网络化运营时代的到来，为了充分利用各条线路的设备资源，减少乘客换乘时间、提高服务质量，组织跨线行车是一个有效的解决手段。因此，研究跨线情况下线网交路优化问题对于提高线网运营组织效率具有现实意义，也可以为后续网络化运营条件下的城市轨道交通开行方案和时刻表的优化奠定基础。以往城市轨道交通交路优化问题的研究以单线为主[1-3]，只有少数研究考虑了跨线运行下的交路优化问题[4]。由于不同的线路设计结构会导致不同的跨线模式，进而对交路优化产生直接影响，为此，在考虑不同跨线模式的基础上，以交路运能和区间客流匹配误差最小、交路距离总和最小以及直达客流量最大为主要目标，构建城市轨道交通线网交路优化模型，最终求解得到交路方案。

1 城市轨道交通跨线模式

在城市轨道交通网络化运营条件下，当2条线路的车辆、信号、供电和通信等基础设备实现互联互通后[5]，在线网中选择合适的跨线站，并在该站配备渡线就可以实现线路之间的跨线运行。按照渡线结构设计的不同情况，跨线站存在3种跨线模式[6]。

（1）单向跨线运行模式。单向跨线运行模式示意图如图1所示，图1中D站为城市轨道交通1号线和2号线换乘站，同时也是1号线和2号线的跨线站。单向跨线运行模式跨线站D线路结构如图2所示，从图2的D站渡线设计结构可以看出，当列车在1号线、2号线之间跨线运行时，只能由1号线A站经D站渡线到2号线B站方向，而不能从A站经D站跨线至C站方向运行，因此跨线交路为A—D—B，将此种情形定义为单向跨线模式。

图2 单向跨线运行模式跨线站D线路结构图Fig.2 Line structure of station D in one-way cross-line operation mode

（2）双向跨线运行模式。如果将D站进行改扩建，双向跨线运行模式跨线站D线路结构如图3所示，可以看出在增加渡线的情况下，1号线和2号线可以完成A站经D站跨线到B站和C站2个方向的跨线运行，因此跨线交路为A—D—B和A—D—C，将此种情形定义为双向跨线模式。

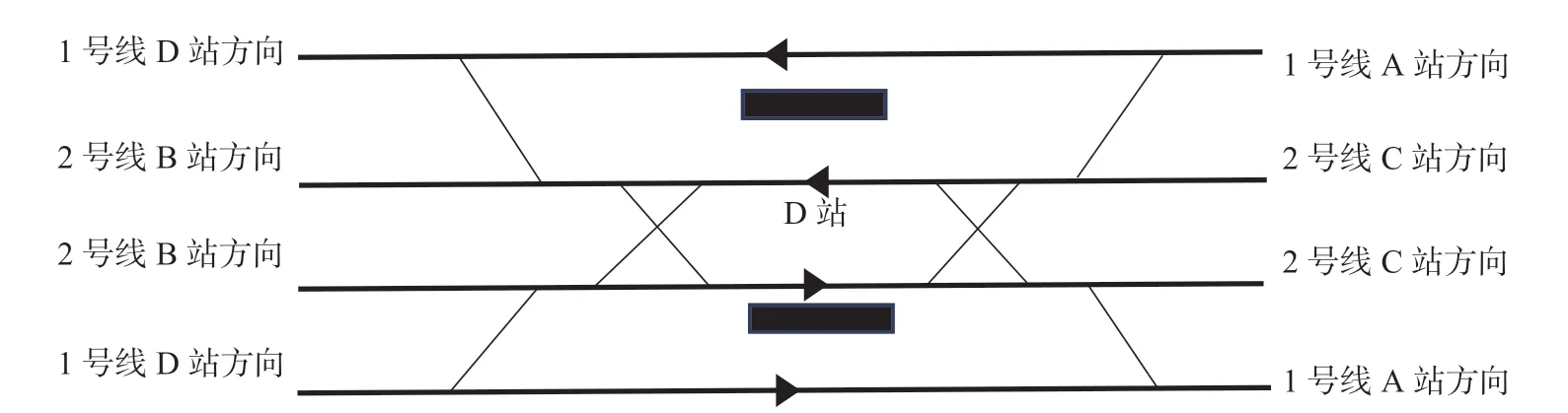
图3 双向跨线运行模式跨线站D线路结构图Fig.3 Line structure of station D in two-way cross-line operation mode

（3）禁止跨线运行模式。目前很多城市早期既有城市轨道交通线路由于制式和车辆类型的不同，无法实现跨线运行，即使基础设施条件允许，但对于建成站点渡线的改造也是极其困难的。因此，在这部分线路间的换乘只能靠步行换乘，在大多数城市中部分既有线路间是不能组织跨线运行的。综上所述，线网的实际情况一般会同时存在3种跨线模式。

为此，研究具有这3种跨线模式的线网交路优化问题。为了便于研究，给出以下假设：假设1——同一区间上下行距离相同；假设2——高峰小时区间断面客流量已知；假设3——OD客流量已知。

2 考虑跨线运行的城市轨道交通线网交路优化模型构建及求解

2.1 城市轨道交通线网交路优化模型构建

在分析城市轨道交通3种跨线模式的基础上，考虑交路覆盖率、区间和车站关联性约束，构建多目标交路优化模型。为便于模型求解，在构建城市轨道交通线网交路优化模型前要先确定交路可选集。一条交路就是要确定其两端具备折返能力的车站，然后再确定交路所经过的中间站，如此找出线网中可能存在的所有交路得到交路可选集，并在一定约束条件下，对交路可选集中元素进行合理选择，使得目标函数最优。

在交路可选集基础上构建的交路优化模型如下。

式中：Q1为交路运能和客流需求匹配度目标变量；K为所有区间集合；pk为区间k断面客流量；xi为交路i是否被选中；zik为交路i是否包含区间k；m为可选交路数量；Q2为所有交路的距离总和目标变量；dk为区间k的距离；S为所有车站集合；gi为交路i包含的区间集合；Q3为不能通过已有交路直达的OD客流总人数目标变量；quv为车站u到车站v的客流量；yij为交路i是否包含车站j；ε为区间或车站允许覆盖的交路数量；k1，k2分别为区间k包含的2个车站。si为交路i包含的车站集合。

式(1)表示交路运能和客流需求匹配度目标，以区间客流不均衡系数和区间交路覆盖率之差的绝对值来度量；式(2)表示所有交路的距离和最小化目标，该目标等价于企业成本最小，这是由于所有交路距离和越小，车辆走行距离也越小，运营成本越低；式(3)表示不能通过已有交路直达的OD客流总人数最小；式(4)表示任意车站至少被一个交路覆盖，但不能超过覆盖上限；式(5)表示任意区间至少被一个交路覆盖，但不能超过覆盖上限；式(6)表示区间和车站关联约束，即区间和其包含的2个车站是一同被选择的；式(7)至式(9)为决策变量0-1取值约束。

2.2 求解算法

上述建立的模型为多目标非线性0-1整数规划模型，对于整个问题的求解算法步骤如下[7]。

步骤1：任意选取S1中2个站点元素，其中S1为折返站集合，然后根据线网拓扑结构和跨线模式情况找出这2个站点元素间的可达路径，考虑到线网条件下两点间路径可能不止1条，则每一条路径就是1条交路ai，如此遍历完S1中任意2个元素的组合后得到A，其中A为交路可选集且A= {ai} (i=1，2，…，m)，ai为第i个交路。

步骤2：利用步骤1得到的交路可选集A，构建式(1)至式(9)的交路优化模型。

步骤3：将多目标模型化为单目标模型，首先将Q2，Q3的量纲与Q1统一成无量纲，把Q2和Q3作归一化处理为再考虑各目标权重关系得到总目标为其中ω1，ω2和ω3分别为各目标的权重系数且ω1+ω2+ω3= 1。

步骤4：利用优化求解器对单目标非线性0-1整数规划模型进行求解，输出决策变量xi，i= 1，2，…，m，算法结束。

3 案例分析

为了验证模型的准确性，进行案例分析。验算线网结构如图4所示。线网共4条线路，共22个站，22个区间，换乘站为2，5，8和11，折 返 站 集 合S1= {1，3，6，7，10，12，13，15，17，18，20，22}，这里选择换乘站为跨线站，则S2= {2，5，8，11}，其中S2为跨线站集合。设定跨线站2和8为禁止跨线模式，跨线站5为单向跨线模式，允许方向为1↔5↔18，跨线站11为双向跨线模式，允许方向为7↔11↔22和12↔11↔22。各区间高峰小时断面客流量及区间距离如表1所示，线网高峰小时OD客流矩阵如图5所示。

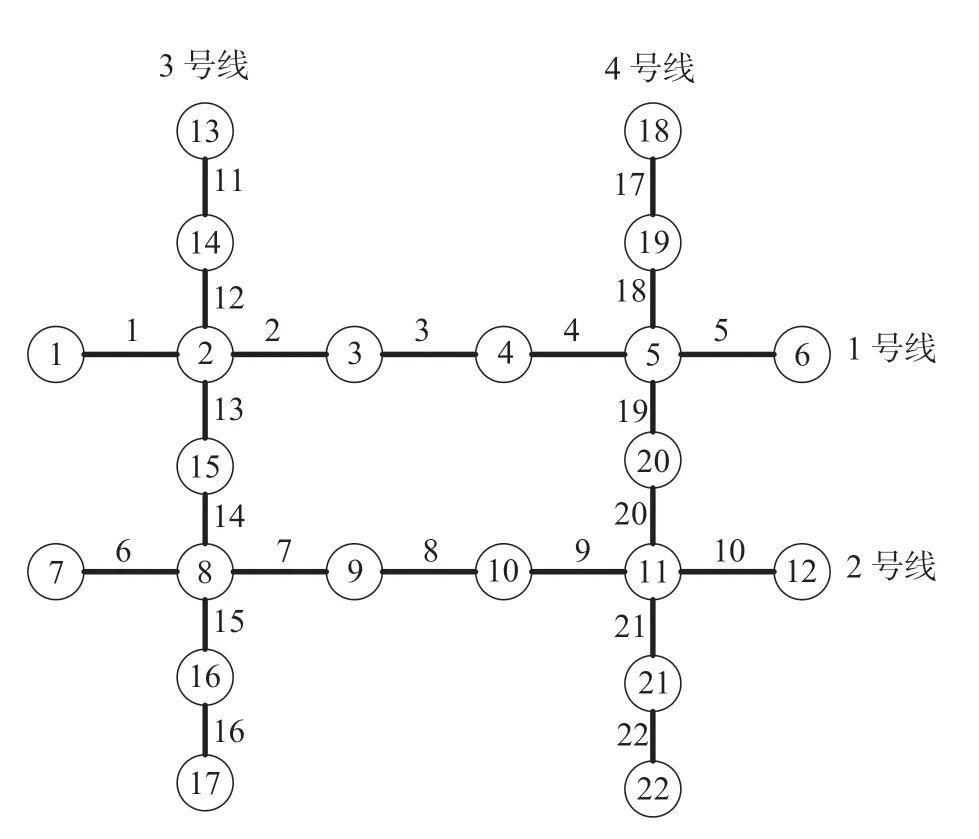
图4 验算线网结构图Fig.4 Structure of checking calculation network

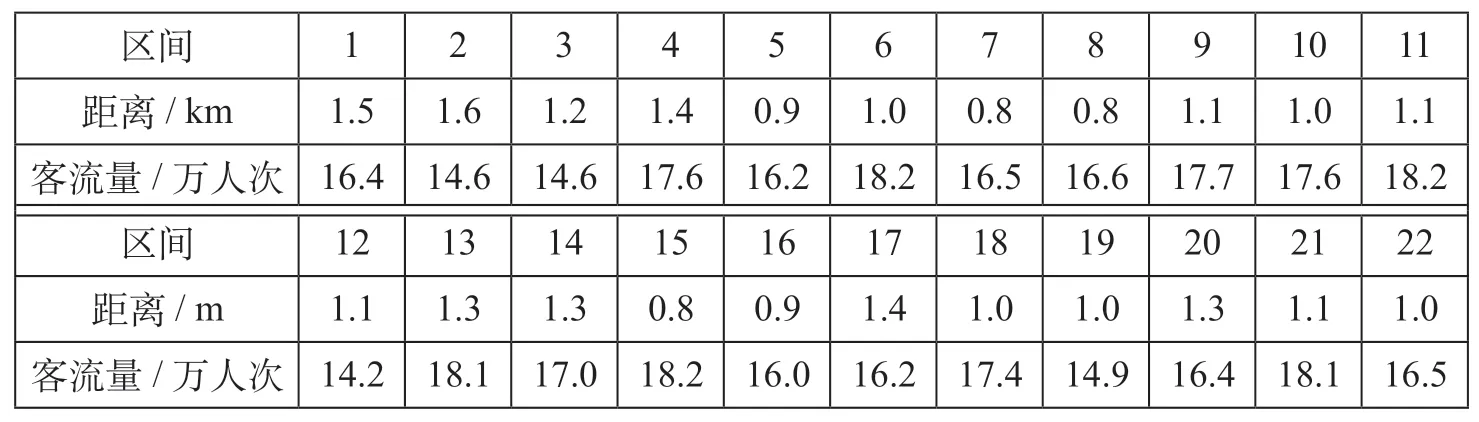
表1 各区间高峰小时断面客流量及区间距离Tab.1 Section passenger flow and section distance in peak hours of each section

图5 线网高峰小时OD客流矩阵Fig.5 OD passenger flow matrix of the network in peak hours

在S1中共有12个折返站，则选择不同折返站的组合数为C122= 66，共66个交路，但考虑到4个跨线站的跨线模式限制，交路可选集为：①1—2—3；②3—4—5—6；③1—2—3—4—5—6；④7—8—9—10；⑤ 10—11—12；⑥7—8—9—10—11—12；⑦13—14—2—15；⑧15—8—16—17；⑨13—14—2—15—8—16—17；⑩18—19—5—20；⑪ 20—11—21—22；⑫18—19—5—20—11—21—22；⑬18—19—5—4—3—2—1；⑭18—19—5—4—3；⑮18—19—5—20—11—10；⑯18—19—5—20—11—10—9—8—7；⑰18—19—5—20—11—12；⑱22—21—11—12；⑲22—21—11—10；⑳22—21—11—10—9—8—7；㉑20—11—12；㉒20—11—10；㉓20—11—10—9—8—7。因此，交路可选集元素个数为m= 23。取ω1= 0.1，ω2= 0.4，ω3= 0.5，再结合表1和图5的基础数据构建式(1)至式(9)交路优化模型，利用软件求解得到交路优化方案和目标函数值如表2所示。

从表2可知，车站和区间允许交路覆盖上限ε取值不同，得到的交路方案也不同。当ε越大，方案中交路数量越多，其中跨线交路也越多。当ε= 4时，方案中有4条跨线交路(⑬，⑱，⑳ 和 ㉓)；当ε= 3时，方案中有3条跨线交路(⑪，⑬ 和 ⑳)；当ε= 2时，方案中只有2条跨线交路(⑱ 和 ㉓)。从目标函数值来看，随着ε的增大，交路数量增多，交路距离总和增加，因此交路距离呈递增趋势。随着ε增大，交路与区间客流不匹配度降低，交路运能和客流需求匹配度呈递减趋势。同理由于方案中跨线数量增加，导致直达客流量增加，非直达客流量呈递减趋势，最终总目标呈递减趋势。考虑到交路之间的干扰、车底数量限制及企业成本等因素，ε不能过大，一般取值不超过4。换乘客流量越大，组织跨线交路的优势越明显，从ε= 2和ε= 3方案中发现它们都包含2条跨线交路(⑬和 ⑳)。交路 ⑬ 完成1号线和4号线间(1，18)，(2，18)，(3，18)，(4，18) OD对客流运输任务。从图5 OD矩阵中统计可知，其客流总量为38万人次，交路 ⑳ 完成2号线和4号线间(7，22)，(8，22)，(9，22)，(10，22) OD对客流运输任务，其客流总量为40万人次。这2部分客流量在路网中属于大客流。如果交路覆盖上限ε允许，则最优化方案倾向于组织跨线交路来提高乘客服务质量。

如果不组织跨线交路，则根据区间断面客流量大小情况在各自线路上组织大小交路模式[8-9]。由表1可知，1号线、2号线、3号线和4号线最大断面客流量区间分别为4，6，11和21，因此按大小交路模式的常规方案为②③④⑥⑦⑨⑪⑫，可以看出在此方案下ε= 3，将该方案与表2优化方案比较，优化方案同常规方案目标函数值比较如表3所示。从表3可知，2个方案交路数量都为8条，优化后的方案比常规方案的交路距离总和增加3.4%，区间客流匹配度增加0.2%，直达客流增加4.6%，总目标增加0.4%。

表2 交路优化方案和目标函数值Tab.2 Routing optimization scheme and objective function value

表3 优化方案同常规方案目标函数值比较Tab.3 Comparison between objective function values of optimization scheme and conventional scheme

4 结束语

对跨线条件下城市轨道交通线网优化进行研究，得到以下结论：通过跨线站模式的划分可以有效减少交路可选集数量，进而降低模型计算复杂度；在合理交路覆盖数上限约束下，增加跨线交路可以使总目标函数降低；虽然总目标函数值在优化后提高不明显，但考虑到城市轨道交通的公益性质，在整体决策上偏向于以提高乘客服务质量为主；由于部分线路禁止跨线，降低了跨线交路的优势，因此在信号、通信、车辆和供电条件满足的情况下，加大对线路的改造、增加线路互联互通性是发挥跨线交路优势的重要手段。在交路优化的基础上制定线网列车开行方案将是下一步的研究目标。