基于六自由度闭环弹道的脉冲多普勒雷达导引头仿真

戴幻尧，马 磊，王德旺，崔建岭

（1.电子信息系统复杂电磁环境效应国家重点实验室，河南洛阳 471003；2.上海机电工程研究所，上海 201109）

0 引言

地空导弹(SAM)作为典型的精确制导武器在现代防空作战中的应用得越来越广泛。很多实验手段包括数学建模、半实物仿真和外场实验等，都有助于SAM的参数设计和性能评估。六自由度闭环弹道仿真提供了一种有效且低成本的解决方案，并且被广大SAM设计人员所采纳。然而，亟须针对SAM的制导和控制回路(GCL)建立足够精确的数学模型，包括动力学特性、导引头、制导律、指令控制、舵机模型和推进器模型[1]，且模型的准确性直接关系到制导的准确性。脉冲多普勒雷达导引头(PDRS)作为关键的角度敏感器件，在现代SAM中有着比较广泛的应用[2]。脉冲多普勒（PD）雷达的工作原理就是相干脉冲发射机利用多普勒效应，获得雷达和目标的相对运动信息，在杂波和接收机噪声中选择指定的目标。然后，PD雷达的一系列窄带滤波器处理由目标反射回的雷达信号，对信号相干合成。PDRS输出的弹目相对视线角(LOS)和视线角速率最终送入制导律生成器中。

传统研究中，为便于简化和计算方便，对PDRS进行功能级仿真不能反映电磁波传播和散射的全过程，也不能再现雷达信号在接收机和数字信号处理机中的相干处理全过程，因此无法满足准确的六自由度闭环弹道仿真需求，特别是无法满足电子对抗条件下的应用需求。与之相比，相干视频仿真能够完整地描述电磁波发射、传播、后向散射、天线接收、接收机处理、数字信号处理和数据处理的全部过程，为SAM的参数设计和性能评估提供了全面和有效的技术途径。由于相干视频仿真具有相当高的计算量，并且研发周期长，因此在六自由度闭环弹道仿真中较少受到研发人员的青睐，导弹空气动力学特性、制导律和指令控制方面的研究更受关注。然而，为了完成精确的闭环弹道仿真，设计人员必须准备一些PDRS的相干视频仿真模型，例如为了评估电子对抗条件下的SAM性能，必须建立足够多的导引头模型，从而分析干扰对导引头命中精度的影响程度。与传统的功能级仿真相比，这样的工作通过PDRS相干视频仿真很容易完成。

本文首先简要地分析和讨论了PDRS作为关键的角度敏感器件在SAM制导控制环路中的作用。然后，讨论了PDRS相干视频仿真涉及的主要内容，包括雷达导引头天线建模、目标散射特性、接收机处理、信号处理器设计和数据处理中的滤波机制。设计了一个六自由度闭环弹道仿真系统，考虑了制导规律和指令控制等关键要素。通过一个典型的防空作战场景对本文给出的模型进行仿真验证，讨论了相干视频仿真和飞行仿真的实验结果。

1 问题陈述

1.1 制导控制环路GNC

图1给出了SAM在交战中所需要的制导和控制回路，需要考虑目标的最大飞行速度、最低高度、隐身性能和操控性能、自卫式电子干扰、自动驾驶仪、舵偏角要求值、空气动力特性等。

图1 地空导弹制导和控制回路

导引头输出的弹目相对运动测量值，将通过指定的制导律，转换为3轴加速度指令，本文所采用的是修正比例导引。由于要获得导弹的实时飞行状态和弹体高度，控制指令单元将会产生控制指令，传送给后续的执行装置。例如导弹打击既定目标时，尾翼为了保持弹体稳定，需要输入加速度要求值。尾翼舵机对转角产生响应，进而达到实际舵偏角。只要舵偏角发生改变，SAM拦截器就会启动空气动力学控制，完成一次六自由度的闭环弹道仿真。

1.2 导引头在制导控制回路中的作用

在SAM的末制导阶段，导引头作为角度敏感器件在制导控制回路中具有重要作用。SAM中携带的有主动雷达导引头，在导引头内部框架坐标系下测量弹目相对距离、距离变化率、框架角和视线角速率。制导寻的的基础就是将导引头测量值转换为加速度要求值。在强杂波和接收机噪声中，PDRS利用多普勒效应来选择和跟踪目标，并且输出连续的和实时的弹−目相对运动测量值。但是，该测量值通常会受到遮挡效应、角闪烁和雷达目标RCS起伏和热噪声的污染。例如，在高重频模式(HPRF)下的导引头，会间断性地产生遮挡损耗，使得测量值周期性地无法利用，这会直接影响制导精度[3]。最坏的情况就是在尾追的情况下，敌方采用自卫电子干扰例如噪声阻塞式干扰或投掷式有源诱饵(TRAD)，在这些雷达干扰的作用下，导引头的目标跟踪回路和制导控制回路会受到中断。因此，在电子干扰寻的应用场景中，导引头需要设计估计器来协助视线角速率的估计，进而维持基本的目标跟踪。

2 视频建模

2.1 PDRS总体思路

根据PD雷达采用的低、中、高重复频率波形，它具有多种不同的工作模式。因此脉冲多普勒雷达导引头设计中最重要的就是脉冲重复频率的选择，PD雷达可以分为低重频（多普勒模糊）、高重频（距离模糊）和中重频（中等模糊）3类。

在多种波形中选择重复频率主要取决于SAM的应用场景。视线角和视线角速率主要用于计算加速度要求值，这是非常必要的，而斜距和距离变化率测量相比较而言就并非绝对需要，尽管在目标跟踪回路和其它先进的制导律中（例如最优制导律）可能会用到该信息。无论弹目相对距离和距离变化率是否正确，只要维持角度跟踪回路的正常工作，PDRS就能够保持基本的寻的制导。

文献[2]的例子指出，小孔径高速弹载雷达导引头采用低重频脉冲多普勒设计会带来主瓣地杂波的谱线扩展的问题，导致目标在频域检测（速度域）产生较大的遮挡。然而，弹载雷达导引头采用中重频(MPRF)设计能够覆盖较宽频谱，既能消除慢速移动目标，又可以覆盖大部分目标方位，提供相对准确的距离信息。但是MPRF会引起距离和多普勒模糊，造成近距离旁瓣进入的回波形成杂波，在相同多普勒区间相互交叠并占据目标回波所处的多普勒单元，提高了多普勒处理的设计难度。HPRF波形能够提供无杂波目标检测区间，从而更容易地分辨速度接近的目标，这对SAM作战场景是非常重要的。HPRF设计需要复杂的方法来解决距离模糊，然而，对于SAM的跟踪回路来说，距离模糊并非关键问题，只需要多普勒滤波器就可以维持目标稳定跟踪。因此，导引头可以通过准连续波处理，在强地杂波和海杂波背景下来选择具有特定径向速度的目标，而不需要距离/距离变化率信息。

通过上面的分析，针对弹载平台采用HPRF波形设计，给出了PDRS相干视频仿真结构实现框图，如图2所示。

图2 雷达导引头技术实现方案

2.2 天线建模

天线建模是PDRS仿真的基础，单个天线的方向图可近似地用辛格函数来表示：

式中，θ是相对于天线波束视线方向的夹角，可以分别表示方位角和俯仰角。θ0为零功率波束宽度，G0是最大增益。公式（1）仅考虑了第一零点内的天线方位图增益，在零功率波束宽度之外的天线增益,例如第一旁瓣和第二旁瓣也可以用sinc函数表示。天线参数设计可以参考实际测量实验的结果，如图3所示。只要单个波束的天线方向图是确定的，就可以计算给定目标方向的和、方位差、俯仰差3个通道的电压增益，以生成相应的回波信号；输出方位差、俯仰差2个通道的测角斜差率，以满足单脉冲天线测角的需要。

图3 导引头天线仿真结果

2.3 雷达目标散射特性

通过高频电磁计算可以对目标散射特性进行准确的建模，例如采用物理光学法计算飞机目标的远场散射特性，主要是后向散射特性。将F-16的实际尺寸作为典型的电大尺寸目标(约70倍波长)，来检验物理光学法的有效性。这里，采用非均匀有理B样条方法(NURBS)来对飞机目标建模[4]和网格剖分。

电磁计算中入射电磁波的频率是15.8 GHz，入射波的俯仰角为90°，方位角从0°到180°均匀变化，变化步长是10°。图4给出了电磁计算得到的散射特性结果，并和Feko计算结果进行了比较。可以看出该类电大尺寸的复杂结构目标能够获得比较高的计算精度，可以用于PDRS建模中导引头天线口径接收到的目标后向散射回波的模拟。

图4 目标散射特性

2.4 接收机处理

如图2所示，通过下变频处理，导引头接收机将目标回波信号从射频转换为中频fIF，距离波门τG用来选择目标回波，从而排除波门以外的杂波和噪声信号。中频滤波器和AGC共同作用，将中频信号序列从叠加的热噪声、干扰、杂波中滤波分选出来，实时地调整接收机中放增益，从而使其输出信号功率落入特定范围中，以满足信号I/Q正交解调处理的要求。不同于传统的雷达导引头中的匹配滤波处理，HPRF设计可以保证谱线之间具有足够的间隔，因而允许对频谱的中心谱线进行多普勒滤波，从而提取和跟踪中心谱线。窄带滤波后的单谱线信号实际上是准连续波，后续的数字信号处理器完成频域的目标检测和跟踪。然而，还需要一个辅助通道来覆盖一个大带宽，这样会有利于抗干扰和杂波抑制[5]。

2.5 数字信号处理

数字信号处理(DSP)包括：杂波对消，时域加权，FFT，频域相干/非相干积累，CFAR检测，主控和角误差测量。导引头通过DSP完成状态控制与逻辑切换，完成了杂波、噪声或电子干扰环境中的目标检测和跟踪，如图5所示。

图5 导引头状态切换和逻辑判断

虽然采用HPRF波形时将产生严重的距离模糊，但是导弹通常不需要距离跟踪回路，因此不需要测量弹目相对距离。距离接近变化率可以在准连续多普勒滤波器中通过跟踪中心谱线来获得，通常需要参考高−低多普勒滤波器输出。通过单脉冲测角处理得到关于天线法线方向的视线角误差。DSP中采取的算法和模型可以参考文献[2,6]。

2.6 数据处理中的跟踪滤波器设计

如第1节所述，导引头需要设计估计器来辅助估计视线角速率。具体而言，估计垂直于视线方向的2个速率分量，是雷达导引头系统的基本工作。文献[3]给出了一种基于修正球坐标系(MSC)角度测量数据的跟踪滤波器设计方法。MSC跟踪滤波器采用一组独特跟踪状态的集合X，包括二维角度、二维角速率以及距变率和距离的比(ITG)，可表示为：

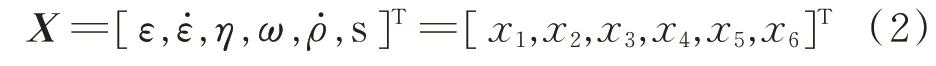
式中ε,η是视线方位角和俯仰角。

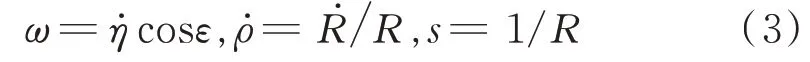
高阶非线性运动方程可以定义如下：

式中，a V T、a H T、a RT是目标垂直加速度、水平加速度和径向加速度，a V M、a H M、a RM对应着SAM的垂直加速度、水平加速度和径向加速度。公式(4)中动态系统的高阶非线性特征导致了传统卡尔曼滤波不再适用。因此，需要对其进行二维扩展。一种方法就是可以采用扩展卡尔曼滤波(EKF)，这是基于泰勒级数展开的一种联合分布，也可以采用基于不敏变换的UKF。为了简化执行步骤，通过简化欧拉积分对式(4)的连续时间动态模型进行了离散化处理。为了提高计算效率，采用龙格库塔积分进行解算会更加方便。

3 闭环弹道仿真器

3.1 制导律

制导律中最基本的是常规比例导引律(PN)。图6给出了防空拦截作战的几何示意图。

图6 作战几何示意图

制导律可以简写为：

式中，N′为有效导航比；V c为逼近速度̇为视线角速率。

公式(5)可以进一步写为：

式中，tgo为飞行时间；y为高度差；ẏ为相对目标率。

括号项代表可能的脱靶距离(不考虑目标机动)，如果SAM不修正加速度，可以称之为零效脱靶量(ZEM)，也就是说如果目标没有机动，那么PN导引率会导致零脱靶量。但是如果目标机动并且加速度为n T，PN仍能保持零脱靶量。PN加速度指令和ZEM成正比，目标机动会修正ZEM。因此，首先要做的就是在要针对目标机动考虑ZEM的一个修正误差项。形成修正比例导引(APN)，可以表示如下：

可以看出，APN制导律需要目标加速度的估计来补偿目标机动带来的误差，还需要估计飞行时间用以解算导引头输出。

3.2 控制律(倾斜转弯控制指令)

根据APN加速度指令，SAM中的控制单元能够生成舵偏角指令。通常采取倾斜转弯(BTT)控制律使导弹指向预定目标并且稳定弹体。实时导弹飞行状态都是需要的信息，包括俯仰和偏航轴的加速度、弹体转速。具体的控制过程比较复杂，可以参考文献[7]。

导弹的尾翼对BTT控制指令进行响应，进而形成实际的俯仰、偏航、横滚通道的舵偏角，SAM的空气动力学特性以及导弹的飞行状态也发生相应的改变，从而完成六自由度闭环弹道仿真全过程。

4 仿真分析

4.1 场景描述

考虑一个典型的空战场景，只关注末制导段，中段制导采用惯性导航，表1给出了部分关键参数。

表1 仿真参数设置

4.2 仿真结果分析

六自由度闭环导弹仿真过程描述如下：将实时的导弹和目标飞机的运动数据送入接收机模型，其它数据包括通过天线模型、目标散射模型、HPRF波形引入的遮挡损耗，弹目径向运动引入的多普勒频移以及距离变化引入的电波传播时间差。经过方位通道和俯仰通道接收到的目标回波通过接收机模型处理后，转换为中频信号。通过窄带滤波器进一步处理提取频谱的中心谱线，并将中频信号转换为I/Q视频序列。杂波对消和后续的多普勒滤波处理有助于中心谱线的跟踪并在速度域形成闭环目标跟踪。利用单脉冲测角模型来提取框架角误差，这些误差信号送入MSC中的跟踪滤波器。一旦完成估计，就可以调整距离波门，多普勒跟踪和角度跟踪回路来完成一次闭环跟踪。初始的视线角速率是通过上面的滤波器估计得到的，寻的制导通过APN制导律完成。通过BTT控制单元生成舵偏角指令，引导导弹朝指定目标寻的并且稳定弹体。尾翼会对角度控制指令产生响应，进而获得实际的三轴舵偏角。SAM受到空气动力学参数控制，综上所述即完成了六自由度闭环弹道仿真。图7给出弹目相对运动的仿真结果。

图7 参考系中弹目相对运动

雷达导引头的相干视频仿真结果如图8所示。归一化频谱清晰地反映了弹目径向速度带来的多普勒频移。通过DSP中的多普勒滤波可以获得该目标速度跟踪回路中的多普勒频移。从SNR曲线中可以看出当导引头采用HPRF波形时会间歇性地产生遮挡效应，使得导引头周期性的无法获得测量值。

图8 I/Q相干视频序列频谱和SNR曲线

图9给出了测量的框架角误差结果，通过单脉冲测角技术可以获得目标关于天线视线方向的角误差，达到较高的测量精度(近似1 mrad)，这保证了寻的制导的精度，提高了抗箔条干扰和投掷式有源诱饵的角度欺骗能力。

图9 框架角误差测量值

角度跟踪阶段，将方位、俯仰框架角误差转换至天线执行系中，从而调整当前的偏航框架角和俯仰框架角。将测量的视线角和真实测量值进行比较，如图10所示，可见该方法具有较好的角度估计精度。然而，在电子对抗条件下，导引头的角度跟踪回路会受到干扰，此时测角性能就会降低。

图10 视线角测量结果对比

4.3 电子对抗情形

在电子对抗条件下，例如在速度波门拖引(VGPO)干扰下，导引头的多普勒跟踪回路会中断，不能正确提取弹目的接近速度，如图11所示，寻的制导精度因此受到影响(脱靶量从2.48 m上升到56.95 m)。可以看出，PDRS相干视频仿真能有效地评估电子干扰对导引头寻的精度和制导精度的影响。

图11 速度波门拖引条件下的速度测量

5 结束语

本文讨论了六自由度闭环弹道仿真中的PDRS相干视频仿真，为SAM的参数设计和性能评估提供了有效的解决方案。■