服务总成本和服务水平均衡的 供应链网络优化研究

何玲辉

摘  要：供应链网络设计和优化对整个供应链运作成本和客户满意度有非常重要的意义，是大型生产型企业和流通型企业关注的重点。对某生产型企业的现有供应链网络进行了梳理，为适应市场需要，公司需要降本增效。文章建立了在满足客户一定服务水平的前提下最小化总成本模型，经过软件运行求解运算，得出了可行的供应链网络设计和优化方案，达到了服务水平和供应链总成本的均衡。

关键词：供应链;网络设计;总成本最低

中圖分类号：F272    文献标识码：A

Abstract： The design and optimization of supply chain network is of great significance to the operation cost and customer satisfaction of the whole supply chain， which is the focus of large-scale production enterprises and circulation enterprises. In order to meet the needs of the market， the company needs to reduce costs and increase efficiency. The model of minimizing the total cost under the premise of satisfying the customer's certain service level is established. Through the software operation， a feasible supply chain network design and optimization scheme is obtained， which can improve the customer service level and reduce the total cost of the supply chain network.

Key words： supply chain; network design; the lowest total cost

市场竞争日趋激烈，客户多样化要求越来越高，服务成本也越来越高。为了适应市场的变化，在减少服务成本的同时满足客户的多样化的精准需求，供应链网络的设计和优化问题应运而生，这成了很多生产型企业和流通型企业当下和今后相当长一段时间内研究的热门课题。

1  模型介绍

供应链网络具体怎样确定一般与相应的目标关联。具体目标一般有：效益最高、成本最低、路程最短、准时性最高、劳动消耗最低等。本文将把服务总成本和服务水平的均衡作为供应链网络设计和优化的主要目标。

本文做出如下假定：（1）客户的位置、需求是固定且已知的;（2）每个设施都能满足客户的全部需求;（3）每个客户的需求只能被一个设施全部满足;（4）存在设施备选集。

供应链网络设计和优化一般可以采用定量分析方法和定性分析方法，对复杂的供应链网络的优化和设计最好是利用线性规划的数学模型转换成计算机程序来求出最优方案。目前，供应链网络设计和优化的方法主要有德尔菲法、部门主管集体谈论法、专家意见加权平均法、表上作业法、图上作业法、蚁群算法、遗传算法、粒子群算法等。

本文采用集合了线性规划模型和混合整数规划模型等方法的供应链商业用软件supplychainGuRu来进行供应链网络设计和优化方案的研究，以服务水平为约束，以总的服务成本最小为目标。为此，建立了如下目标函数和数学模型。

目标函数：

Min总成本=Min运输成本+设施成本=需求量*单位运输成本+单位设施可变成本+设施固定成本

数学模型为：

min∑∑trans+facVardY+∑∑facVarFixX

s.t.

∑Y=1; ？坌∈J                                                             （1）

∑∑X=P                                                              （2）

∑X≤1; ？坌∈I                                                           （3）

Y≤∑X; ？坌∈I    ？坌∈J                                                （4）

∑∑dist>HighServiceDist？0：1）dY≥HighServiceDemand                        （5）

Y∈0，1; ？坌∈I    ？坌∈J                                                   （6）

X∈0，1; ？坌∈I    ？坌w∈W                                                 （7）

決策变量：

X：是否在位置i使用规模为W的设施;

Y：设施i是否为客户j服务。

约束条件：

（1）客户J需求一次性全部满足;

（2）设施数量为P个;

（3）每个地点的设施在W个规模下至多选1个;

（4）提供服务的设施必须已经开放;

（5）一定距离内满足客户需求不低于某个百分比。

模型中的目标函数为总成本最小，其中总成本包含三项：设施建设的固定成本和设施运行过程中的可变成本及运输成本。服务水平指的是一定条件下满足客户要求的供应链服务的数量占总客户订单数量的百分比，主要参数指标是满足的客户流量（单位为件，下同）占总客户流量的百分比，模型中用百分比来表示。

2  案例算法

A是一家建材产品的生产企业，企业主要生产6种产品：A1、A2、A3、A4、A5、A6。为遍布全国的385个门店服务，门店需求以一年的总流量来衡量，其需求分布如图1所示。将需求按省份汇总如图2所示，颜色越深代表该地的需求量越大。

该企业现在已经确定了25个可供选择的潜在仓库，其地理位置坐标如图3所示，绿色三角形代表潜在仓库的位置，希望在25个潜在仓库中选择目标仓库来满足企业的要求。

公司根据有关主要道路和交通方式的公共信息，确定了送货卡车的平均行驶速度仅为60公里/小时。 将这些信息与驾驶员每天最多只能工作8小时的假设相结合，能够计算出等效的一日乘车距离：一天60公里*8小时=480公里。

随着公司业务的不断发展，面临的竞争也越来越大，公司需要进一步提升服务水平，同时也需要考虑成本。公司计划在全国范围内优化网络布局，以达到期望的服务水平，并获得为此需要付出的成本情况。

根据调研，公司将期望服务水平定为一天半内满足客户，即客户距离站点需要在720公里之内，本文将以这数据作为参考进行供应链网络设计和优化的基础数据之一。

本文拟建立以下六种情况来比较不同条件下的选址方案（均以720公里作为条件之一）：

（1）以总成本最低为目标。假设仓库到各个门店的费率一致，经过调研，取全国统一运输费率为0.05元/件，千米;

（2）以总成本最低为目标。全国各仓库到门店的运输费率根据当地的实际情况确定，为模型计算考虑，取一个仓库到各门店的运输费率统一，不同仓库运输费率有区别（前期已把数据做了处理，如表1）;

（3）满足服务水平93%的最小总成本的可行的选址方案;

（4）满足服务水平94%的最小总成本的可行的选址方案;

（5）满足服务水平95%的最小总成本的可行的选址方案;

（6）满足服务水平96%的最小总成本的可行的选址方案。

其中第三到第六种情况都是在分区费率情景下进行网络优化。

假定仓库的固定成本为200万元/个，仓库的可变成本为阶梯成本，如表2所示。

模型所需要的客户订单信息等由于数据庞大，不在文章中一一列表，在软件运行之时会导入系统。

2.1  第一种情况：统一运输费率下的供应链网络优化

以总成本最低为目标，单位运输成本取为全国各地一致：0.05元/件，千米。

输入数据，运行模型，该条件下选择了11个仓库，分别是哈尔滨、咸阳、广汉、深圳、郑州、营口、岳阳、石家庄、杭州、安徽、昌吉，如图4所示。

这种情况下总成本最小时各个仓库运行成本及各个仓库到客户的物流流量等如表3所示。

最小总成本模型下，一天半之内（720km之内）满足的客户需求占比为95%，即服务水平为95%。

2.2  第二种情况：费率分区环境下的供应链网络优化

此时按各地实际费率情况分区进行单位运输成本核算，还是以最小总成本为目标。

此情况下，一天半之内（720km之内）满足的客户需求占比为92%，即服务水平为92%。

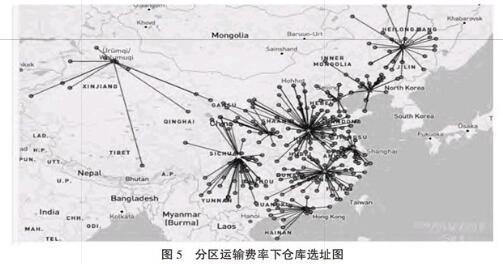
此时开启的仓库是十个：哈尔滨、广州、泰州、咸阳、广汉、郑州、营口、南昌、天津，昌吉如图5所示，分区运输费率下优化结果。具体情况见表4所示。

2.3  第三种情况：720公里范围内，服务水平为93%的最小总成本为目标的供应链网络优化

此时开启十个仓库，仓库为：哈尔滨、广州、泰州、咸阳、广汉、郑州、营口、南昌、天津，昌吉，具体结果如图6和表5所示。

2.4  服务水平94%下网络优化。

此时开启的仓库为十个：哈尔滨、广州、泰州、咸阳、广汉、郑州、营口、南昌、天津、昌吉。具体情况如图7和表6所示。

2.5  服务水平为95%网络优化

此时开启十个仓库：哈尔滨、广州、泰州、咸阳、广汉、郑州、营口、南昌、天津、昌吉。具体如图8和表7所示。

2.6  服务水平96%时网络优化

此时开启12个仓库：哈尔滨、广州、泰州、咸阳、广汉、郑州、营口、南昌、天津，石家庄、昌吉、重庆。具体如图9和表8所示。

3  总  结

以最小化总成本为目标，不同的情况下，总成本和服务水平如表9所示，不同服务水平下的总成本曲线图如图10所示。

当服务水平每提高1%时，模型的总成本的增加率如表10所示。

分析：（1）因为各地情况不一，费率难以符合真实情况。因此，统一运输费率不适合全国范围内网络优化，成本较高。（2）以最小化总成本为目标进行仓库选址，同时添加服务水平的限制，可进行成本和服务水平的权衡。

一般情况下，随着服务水平的提升，运输成本的不断减少，仓库的总成本不断增加。本优化过程基本符合这一趋势。在服务水平为95%时成本略微降低，据分析，这是由于低运输费率的仓库运输货物较多，从而使得总运输成本较低，进而使得总成本偏低，这在实际工作中也会遇到。

（3）服务水平每提高一个百分点，总成本的增加率是不同的。本文方案中，服务水平为93%和95%时的方案较好。

参考文献：

[1]  SHAH N. Single and multisite planning and scheduling： current status and future challenges[J]. AIChE symposium series， 2008，94：75-90.

[2] 韩喜艳，高志峰，刘伟. 全产业链模式促进农产品流通的作用机理：理論模型与案例实证[J]. 农业技术经济，2019（4）：55-70.

[3] 王萍，张慧，颜清. 海南热带水果产业生态供应链模型构建[J]. 热带作物学报，2017（8）：1578-1581.