基于RSA算法的加密通信研究与应用

宋杨

（辽宁轨道交通职业学院，辽宁沈阳，110023）

1 背景

传统的加密方式是对称加密。对称加密的特点是加密和解密用同一个密钥。用户A用密钥K将明文M加密得到密文E；然后用户A 将密文E 和密钥K 同时发送给用户B；用户B 从收到的消息中提取出密钥K 和密文E；用密钥K 对密文E 进行解密得到明文M。由于加密和解密用同一个密钥，因此只要密钥泄露，黑客就可以用密钥K 对通信双方的密文进行解密，用户A 和用户B 之间的通信就不再安全。

对于BS（Browser-Server）结构的系统，如果每个客户端用同样的密钥，那就等同于用明文通信；如果为每个客户端生成一个不同的密钥，在对称加密情形下，服务器需要知道每个客户端的密钥，这么做是不现实的，因此，需要一种非对称的加密的方式。假设有公钥pub 和私钥pri，私钥由服务器保存，公钥可以自由分发，在客户端访问服务器的时候可以由服务器将公钥pub 分发给客户端。公钥加密的消息只能由私钥解密，反之，服务器在发送消息给客户端前，需要用私钥将消息加密，客户端收到服务器的消息后用公钥解密。由于私钥保存在服务器上，只要服务器不被攻陷导致私钥泄露，客户端与服务器之间的通信就是安全的（还需要防范中间人攻击）。RSA 算法就是这样一种非对称加密算法，该算法在1977年由Ron Rivest、Adi Shamir 和Leonard Adleman 一起提出，RSA 就是他们三人姓氏开头字母拼的组合[1]。

2 RSA 算法的原理

2.1 欧几里得算法

欧几里得算法也叫做辗转相除法，可以用此算法快速求的两个数的最大公约数。欧几里得算法用公式表示为

公式1 中，gcd(m,n)表示求m 和n 数的最大公约数，m%n表示m 除以n 的余数。该公式的含义是整数m 和n 的最大公约数等于整数n与m除n余数的最大公约数[2]。公式-1的证明过程如下：

公式-1 的Java 实现如下所示，这是一个递归函数。

2.2 扩展欧几里得算法

对于正整数m 和n，一定存在整数对x 和y，使得公式-2成立，公式2 被称为贝祖定理。

扩展欧几里得算法就是在用欧几里得算法计算公式-2的过程中求得二元一次方程的整数解。证明如下：

根据欧几里得算法可知gcd(m,n)=gcd(n,m%n)

如果公式-2 成立，那么nx+(m%n)y=gcd(n,m%n)

假设有一对正整数解x1和y1使得mx1+ny1=gcd(m,n)

另有一对正整数解x2和y2使得nx2+(m%n)y2=gcd(n,m%n)

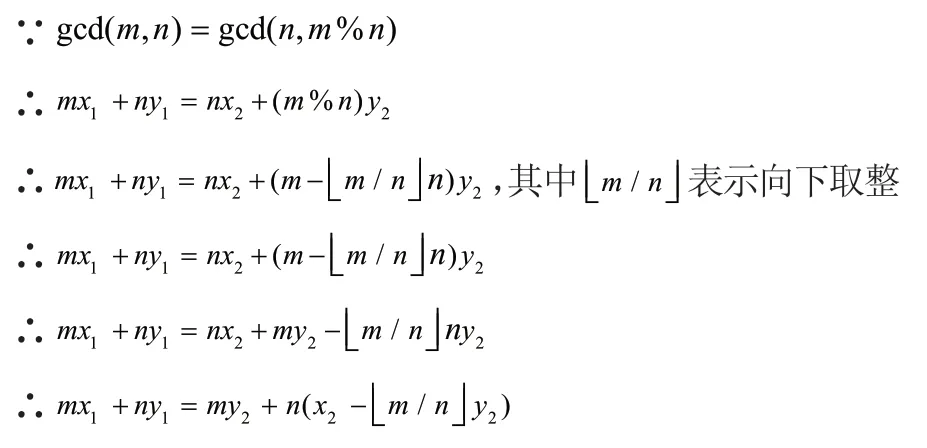
从公式-3 可以看出，这是一个递归求解过程，当递归到n= 0时，二元一次方程出现了明确的整数解，递归回滚，因此可以求得公式-2 的整数解。此时，x= 1,y 为任意整数，y 取不同的值，会求得不同的整数解，因此公式-2 的整数解有多个。解扩展欧几里得算法的Java 实现如下，形参m 和n 分别对应公式-2 中的m 和n，形参x 和y 分别对应公式-2 中的x和y。

2.3 素数的查找

只能被1 和自身整除的正整数被称为素数。素数在生成RSA 密钥对的过程中有非常重要的作用。判断正整数p 是否为素数，根据定义，只要找到正整数n(1

2.4 欧拉函数

欧拉函数定义为在小于n 的正整数中与n 构成互质关系的整数的个数。m 和n 互质，就是m 和n 的最大公约数为1，欧拉函数表示为ϕ(n)。例如：ϕ(8) = 4，因为1、3、5、7 与8互质。欧拉函数的计算公式如下，其中P 和Q 均为素数。

根据欧拉函数的定义，公式-4 就是要找出在区间(1,PQ)内找到与PQ 互质的正整数。那么可以先找到与PQ 不互质正整数的个数k，然后再用PQ−k即可求得ϕ(PQ)。在区间(1,PQ)内，包含P 的倍数的正整数有P、2P、3P...(Q-1)P、QP，总计Q 个；同理，包含Q 的倍数的正整数的个数是P 个。以上两个计数的过程中多计算了一个PQ，因此与PQ 不互质的正整数的个数是P+Q− 1。因此，ϕ(P×Q)=PQ−(P+Q−1)=(P−1)(Q−1)。

2.5 RSA 算法的加密与解密过程

第1 步，借助（三）的内容，随机挑选两个素数，所挑选的素数越大越好。这里挑选P=269，Q=347。计算n=P×Q=269 ×347 =93343，93343 转换成二进制数就是1 0110 1100 1001 1111，总计13 位，此时的RSA 算法就是13位加密。在工程应用上，通常采用1024 位加密，要求更高的场合，例如金融领域会采用2048 位加密，加密位数越大越难以破解。

第2 步，借助（四）的内容，计算n=93343的欧拉函数ϕ(n) =268 ×346 =92728。

第3 步，随机选择一个正整数e，e 需要满足的条件是1

第4 步，找到一个整数x 使得e×x%ϕ(n) = 1，也就是e×x− 1=ϕ(n)y，整理得

本例中，e=17719，ϕ(n) =92728，公式-5变为17719x−92728y= 1，求此二元一次方程的一对整数解即可得到密钥对。

第5 步，借助（二）的内容，可求得一对整数解(x,y)= (21561,4120)。不同的e 可以生成不同的x。本例中，(n,e)= (93343,17719)是公钥，(n,x)=(93343,21561)是私钥。公钥可以公开，如果只知道n 和e，将非常难以推断出x， ( )nϕ越大越难于推断出x，也就越难以破解。

第6 步，加密和解密过程分别如公式-6 和公式-7 所示。src 表示被加密的明文，是一个整数；e 是公钥(n, e)中的e，x 为私钥(n, x)中的x，n 为欧拉函数 (nϕ)中的n，encrypt 表示密文，decrypt 表示解密后的明文，pow 表示幂运算。

例如，中文“世”字的UTF-8 编码为[E4,B8,96]，对应的十进制编码为[228,184,150]，将此三段十进制数字分别进行加密得到，

解密过程为。

从以上加密和解密的过程中可以看出，其中涉及到了大整数运算，无论何种编程语言其数据类型都会有一个取值范围，直接进行这样的大整数运算不是明智的选择。公式6 和公式7 的计算过程可以用公式8，即模运算的分配律[3]避开大整数的运算。

因此

从公式9 可以看出，可以用递归函数实现公式-6 和公式-7的加密与解密过程。进行大整数模运算的Java实现如下。

3 RSA 算法的应用

以BS 结构为例，服务器端生成公钥和私钥。在浏览器向服务器索取网页时，服务器将公钥存放在网页中发送给用户A。用户A 在发送消息给服务器的时候用公钥给明文加密，再将密文发送给服务器。在A 的发送过程中，如果密文被黑客B截获，B 无法破解A 发送的密文。因为经RSA 算法公钥加密的密文必须由私钥解密，虽然B 可以获得服务器分发的公钥，但是经公钥加密的密文不能由公钥解密。服务器收到A 发送的密文后，用私钥将其解密，将处理结果用私钥加密后再发送给A。这时就可能存在风险，如果服务器返还给A 的密文被B 截获，虽然B 无法解密A 发出的密文，但是B 有公钥，可以解密服务器发出的密文。通过将服务器发出的密文解密，B可以得到对自己有潜在价值的信息，这样就有可能对A 产生不利影响。

为了避免服务器返回的密文被B 截获并用公钥破解，A也可以主动利用RSA 算法生成密钥对，将生成的公钥做好起止标记放在明文的某个位置，用服务器分发的公钥给这个新的明文加密后再发送给服务器；服务器收到密文后用自己的私钥解密，按照起止标记提取出A 分发的公钥，用此公钥给处理结果加密，将密文返回给A。虽然B 可以截获此密文但是无法破解，因为此密文不是用服务器的私钥加密。当A 收到服务器返回的密文后，用自己保存在网页中的临时私钥将密文解密得到明文，这样就保证了通信的安全性。

目前，无论前端还是后端开发，都有成熟RSA 算法库可用。例如在前端开发中，可以使用Javascript 编写的开源库jsencrypt，在网页上使用时，需要先用