基于属性数学理论的岩质边坡稳定性评价

杨 涛

（四川省煤田地质局135队，四川泸州646000）

1 概述

岩质边坡处于一个复杂而开放的系统当中，其工程地质性质受多种因素的影响和控制，具有很强的不确定性和模糊性，这决定了边坡岩体的变形破坏特征是极为复杂的，因此，应用经典的数学模型来评价边坡的稳定性存在着明显的缺陷。传统的岩质边坡稳定性评价方法强调从结构面的角度出发建立岩质边坡稳定性评价体系，利用定性和定量的评价方法，对边坡稳定性做出综合的评价，但对于实际情况中存在的模糊不确定性因素考虑不足，所得的评价结果往往不能反映出边坡真实的稳定性状况。为此，众多学者将不确定性的评价方法引入到边坡稳定性评价当中，包括灰色聚类分析[1]、层次分析法[2]、模糊综合评价[3]、可拓学理论[4]等，各种方法的侧重点不同，但都普遍存在着自身的局限性，如评价指标的选取和权重的赋值带有很大的主观性质，模糊综合评判存在最大隶属度失效的问题[5-6]等。属性数学理论以属性集、属性测度空间和属性识别为基础，可以实现对定性描述的度量和有序分割类的识别。本文基于属性数学理论，建立起岩质边坡稳定性评价模型，构造属性测度函数，以相似数[7]的方法确定各评价指标的权重，然后获得综合属性测度，用置信度准则进行岩质边坡稳定性的判别和评价。经过工程实例验证表明：评价结果基本符合实际情况，这为科学的评价岩质边坡的稳定性提供了一种新的思路和方法，对于类似的工程具有借鉴意义。

2 属性数学评价理论

属性数学理论是我国程乾生教授[5-6]提出的，它可以解决某类具有多个模糊属性的综合评价问题。属性数学评价模型包括单指标属性测度、多指标综合属性测度和属性识别三部分。设x为评价对象空间，xi(i=1,2,…,n)为评价空间x的第i个评价对象，其有m个评价指标I j(j=1,2,…,m)和与之相对应的测量值t j，对于测量值t j，都有K个评价等级C k(k=1,2,…,K)。属性评价空间F={评价等级}=(C1,C2,…,C K)，评价空间内每一种情况为一个属性集,例如将岩质边坡的稳定性评价等级分为C1={Ⅰ级}={稳定}、C2={Ⅱ级}={较稳定}、C3={Ⅲ级}={基本稳定}、C4={Ⅳ级}={不稳定}、C5={V级}={极不稳定}。评价对象的属性级别用属性测度来表示，因此可以用属性测度值来定量化确定t ij的评价等级。由于属性测度之间满足相加性规则，从而可以对评价对象x i进行综合属性评价。

2.1 单指标属性测度

设评价指标I j的测量值为t j，具有属性级别C k，其属性测度值μijk=μ（t ij∈C K），按照属性测度的性质，μijk需满足：

对指标I j建立对应的属性测度函数，以表示属性测度的变化情况。用表1中的形式来建立属性测度函数。

表1 单指标等级划分

表 1 中 ，a jk满 足a j0＜a j0＜…a jk，或a j0＞a j0＞…a jk。令

当a j0＜a j0＜…a jK时，单指标属性测度函数参考文献[8]；当a j0＞a j0＞…a jK时[9]，根据公式（2）～（4）形式构造单指标属性测度函数：

式（2）～（4）中 ，k=1,2,…,K-1 ，j=1,2,…,m。

2.2 多指标综合属性测度

对于评价对象x i各单指标的属性测度μijk=μ（t ij∈C K），其综合属性测度由加权求和得到。μxk可按下式计算：

式中：ωj——第j个指标I j的权重，满足0≤ωj≤1，

用相似权方法确定各评价指标的权重。首先假定评价对象x i各单指标的权重相同，即令ωj=1/m，由式（5）求出指标综合属性测度评价矩阵，若单指标属性测度(u i j1,u ij1,…,u ijK)与综合属性测度(u i1,u i1,…,uiK)越近似，则表明I j越能反映总体情况，其权重越大。令r j为相似系数，ωj为相似权，由公式（7）和（8）求得，相似权ωj可作为评价指标I j的权重。最后将相似权值重新代入公式（5）求得综合属性测度。

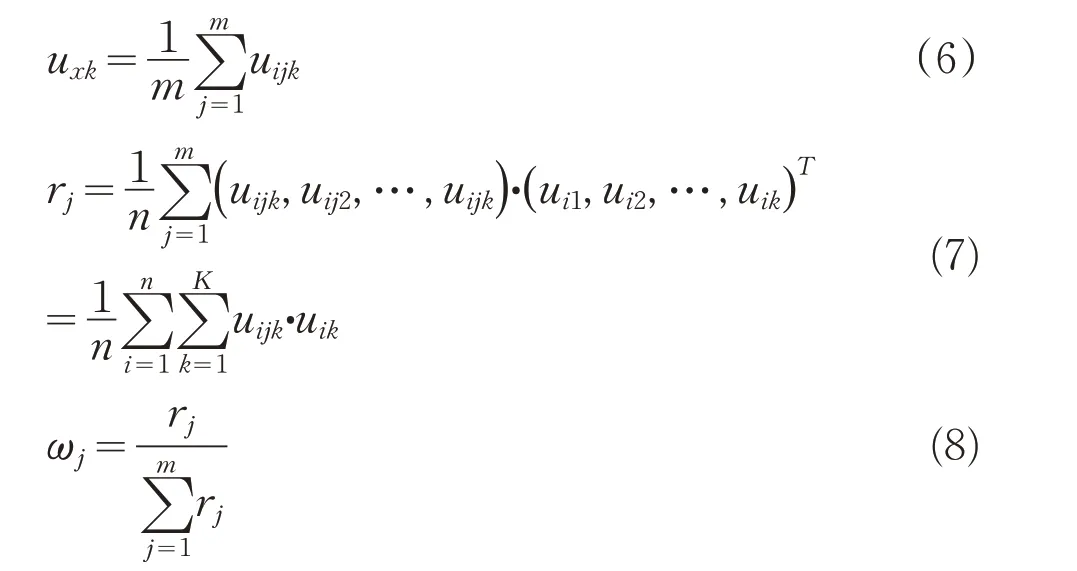
2.3 属性识别

在属性综合评价中，如果(C1，C2，…，C K)为属性空间F的分割，并且满足C1＞C2＞…＞C K或C1＜C2＜…＜C K，则称(C1，C2，…，C K)为有序分割，一般采用置信度准则判定评价对象x i属于哪一个评价等级C K。置信度准则：设λ为置信度，且0.5＜λ≤1，一般取0.6～0.7之间。

当C1＞C2＞…＞C K时，若满足：

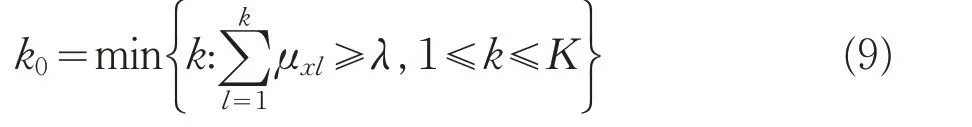
则认为x属于C K0级别。

当C1＜C2＜…＜C K时，若满足：

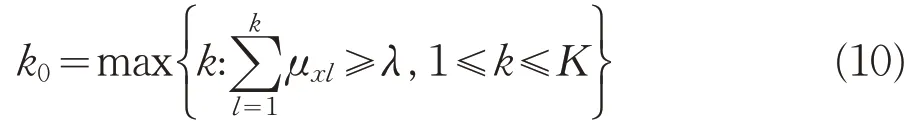
则认为x属于C K0级别。

3 岩质边坡危险性评价指标体系

3.1 评价指标的选取[4]

岩质边坡的稳定性受岩体的结构特征、岩性、地形地貌和应力环境等多种因素的综合影响，某些因素对边坡的稳定性起控制性作用，某些因素则是边坡失稳破坏的触发因素。文中岩质边坡的稳定性评价选取7个评价指标：I1={RQD}；I2={岩体结构特征}；I3={地应力}；I4={内聚力}；I5={内摩擦角}；I6={坡高}；I7={日最大降雨量}；将岩质边坡稳定性等级分为稳定、较稳定、基本稳定、不稳定和极不稳定5个等级，各指标评价等级划分见表2。

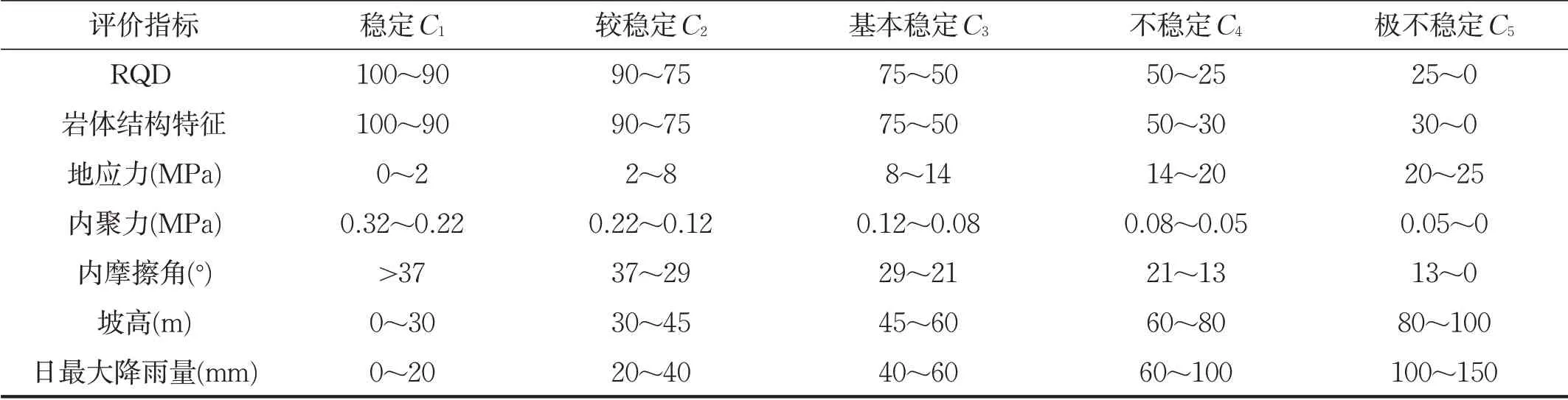
表2 岩质边坡稳定性评价指标和分级标准

3.2 评价指标的属性测度分析

以首钢某区域的边坡[4]为例，进行岩质边坡稳定性属性识别分析。该区域出露地层以变质岩为主，地质构造复杂，选取三类岩质边坡作为待评价边坡，进行边坡稳定性属性识别分析，见表3。根据公式（2）～（4），结合表2中的分类标准来构造单指标属性测度函数，限于篇幅，文中仅列出评价指标I1的属性测度函数，如下所示。

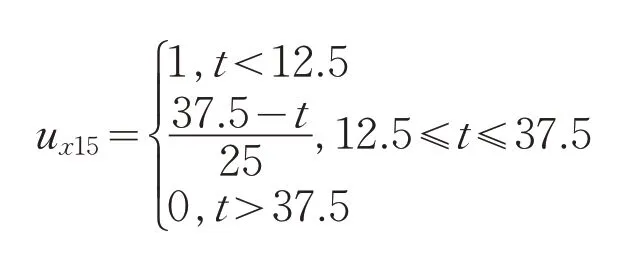
表3 待评价边坡评价指标值

根据表3中的数据和构建的属性测度函数，可求得各评价对象的单指标属性测度评价矩阵。以评价对象x1为例，将测量值代入属性测度函数中，计算可得x1的单指标属性测度评价矩阵。首先假设各项指标的权重相等，得到各单指标的权重为1/7，依据公式（6）～（8）计算可得到相似数：(0.362，0.387，0.328，0.337，0.218，0.276，0.143)，然后得到5个指标的相似权：（0.176，0.189，0.16，0.164，0.106，0.135，0.07），即为各项指标的权重，最后计算得到评价边坡x1多指标综合属性测度，见表4。

表4 边坡x1属性测度分析

3.3 属性测度分析

属性识别分析就是由多指标综合属性测度u xk判断评价对象属于哪一个评价级别，取λ=0.65，根据公式（9）进行属性识别，可以判定边坡x1的危险性等级为C3，即较稳定。依次可得到各评价样本的属性识别结果，基本符合实际情况，见表5。将评判结果与文献[4]中的评价结果对比，可以看出属性识别结果与物元可拓评判结果有较好的一致性，这表明利用属性识别分析来评价岩质边坡的稳定性是合理和可信的。

表5 属性识别结果

4 结论

（1）基于属性数学理论，建立岩质边坡稳定性评价模型，为岩质边坡稳定性评价提供了一种新的思路和方法。选取7种因素作为边坡稳定性评价的指标，构建属性测度函数，获得指标的属性测度值，利用置信度准则进行属性识别分析。该方法理论基础严谨，数学意义明确，具有较强的实用性。同时该评价模型采用相似数方法获取指标权重，避免了传统权值确定的主观性和随意性，从而保证了评价结果的客观性和准确性。

（2）通过工程实例验证，并与物元可拓评判结果对比，结果表明二者评判结果基本一致，表明该模型的评价结果是准确可信的。岩质边坡的稳定性受多种因素的影响，其发展演化过程具有高度的不确定性，因此，其评价指标的选取和分级以及权重的确定等方面还需要进一步的研究。