路基边坡雨水浸透变形模拟研究

冯振华，王利超，韩玉龙

摘要：为了减少由于雨水渗透引起的路基边坡局部变形和失稳现象，在概述模型实验现象的基础上，采用饱和及非饱和渗流分析方法以及弹塑性有限元分析方法，模拟路基边坡模型中水位的变化和滑动破坏发生前的初始变形，建立渐进式边坡失稳的预测方法，通过实验进行再现分析，以明确边坡初始变形机理。研究结果表明：1）在饱和及非饱和渗流模拟中，当渗流系数设置值比渗透实验结果大时，模型实验的再现性良好;2）在弹塑性有限元分析中，通过边坡水位升高导致变形系数（刚度）减小，进而能够分析出模型实验中边坡的初始变形。研究过程为分析降雨期间路基边坡稳定性提供了新方法，其结果可为工程施工过程中避免发生大规模崩塌现象采取适当措施提供依据，为施工标准的设计和制定提供重要参考。

关键词：岩土工程;降雨模型实验;初始变形;饱和及非饱和渗流分析;弹塑性有限元分析

中图分类号：TU45文献标识码：ADOI： 10.7535/hbgykj.2021yx05004

Simulation research on rainwater infiltration deformation of

roadbed slope

FENG Zhenhua，WANG Lichao，HAN Yulong

（Henan Transportation Planning and Design Institute Company Limited，Zhengzhou，Henan 450000，China）

Abstract：In order to reduce the local deformation and instability of subgrade slopes caused by rainwater infiltration，on the basis of an overview of the model experiment phenomena，the saturated and unsaturated seepage analysis and the elastoplastic finite element analysis were used to simulate the change of water level in the roadbed slope model and the initial deformation before sliding failure.Then the progressive slope instability prediction method was established.Finally，through the reconstruction analysis of the rules with experiments，the initial deformation mechanism of the slope was clarified.The results show that：1） in saturated and unsaturated seepage simulations，when the seepage coefficient is set larger than the result of the seepage test，the reproducibility of the model experiment is good;2） in the elastoplastic finite element analysis，the deformation coefficient （stiffness） can be reduced by increasing the water level of the slope，thereby the initial deformation of the slope in the model experiment can be analyzed.The study provides a new way for analyzing the stability of roadbed slopes during rainfall，and the results can provide a reference for taking appropriate construction measures to prevent the occurrence of large-scale collapse，which is also beneficial for formulating future construction standards.

Keywords：geotechnical engineering;rainfall model experiment;initial deformation;aturated and unsaturated seepage analysis;lastoplastic finite element analysis

河南地區每年7—9月为雨季，近年来大部分地区中雨、大雨以及暴雨日数呈增加趋势，自然灾害频繁。极端降水会引起路基土体结构变形、坍塌，对公路路基影响巨大，严重影响交通运输安全。

豫东地区土质多为粉质砂土，降雨过程中边坡土体结构破坏的状况主要通过模型实验进行分析，确定边坡的稳定性[1-3]。对降雨过程中边坡水位变化和崩塌机理的研究发现，粉质砂土边坡的稳定性分析大多基于完全刚塑性体的极限平衡假设。但在全尺寸模型[4]和离心机模型[5]实验中，使用由粉质砂土模型边坡进行降雨滑坡实验，随着降雨造成的边坡中的水位和孔隙水压力的增加，边坡会在某时间点发生局部变形，之后破坏逐渐向边坡上部延伸，最终导致土体大规模滑动，即渐进式边坡失稳。此类研究中的边坡破坏形态并非极限平衡法中所假设的瞬间滑动。在渐进式破坏发生前，坡面还出现了裂纹和局部变形。考虑到实际边坡状况，需要采取适当的施工方案以便在初期变形前防止土体大规模滑动崩塌发生。因此，阐明初始变形的机理，建立边坡渐进式破坏的预测方法显得尤为重要。

近年来SPH法等粒子分析方法在对边坡渐进式失稳的分析中被证明是有效的，并得到了坍塌滑动过程中的影响因素分布的结论[6-8]。但在粒子分析方法中，需要的参数更多并且难以从现场实验勘测和室内土力学实验中获得。因此，通过有限元法简单地再现边坡渐进式失稳具有更大的实际应用价值。

本研究对模型边坡实施了人工降雨实验，记录了降雨过程中坡体的饱和度和孔隙压力变化，并进一步通过饱和及非饱和渗流模拟再现了模型边坡中的水位变化，并尝试通过弹塑性有限元法再现粉质砂土边坡模型中水位上升引起的边坡初始变形来研究其整体变形机理。在弹塑性有限元分析中，主要针对岩土材料的变形系数展开研究，并假设边坡地下水位升高时，变形系数随有效应力的减小和应变的增加而产生折减。

1降雨边坡模型实验

1.1模型概要

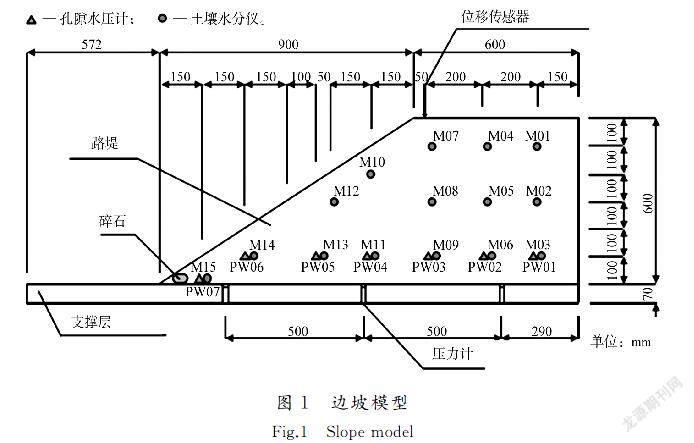
边坡模型的概略图如图1所示。

水平支撑地层厚为70 mm，在其上制作了坡度比为1∶1.5，高600 mm、宽600 mm的边坡模型，并在土箱壁上涂抹硅脂，从而减小摩擦。模型中使用的土体材料取自河南省道323高家沟大桥附近的粉质砂土（土粒相对密度s=2.683 g/cm3，平均粒径D50=0.165 mm，不均匀系数Uc=2.59，曲率系数U'c=1.32，细粒含量（质量分数）Fc=10.8%，最大干密度dmax=1.533 g/cm3，最优含水率w = 19.5%），制作方法为普罗克特压实法，干密度d /最大干密度dmax×100%=95%，w=19.5%。以边坡体压实度Dc=75%，w=13.0%为目标，每次铺设50 mm厚度土层，然后用振动器压实后再进行下一层土层的铺设。研究中，在坡箱底部放置一层平均直径约10 mm的砾石材料，以防止由于水位快速上升发生渗透崩塌。

在边坡模型的坡顶安装位移计，在坡体中安装孔隙水压计和土壤水分仪用于测量土体含水量变化，仪器安装布置如图1所示。降雨量设置为40 mm/h，降雨持续450 min，其后采用洒水降雨。在支撑土层的3个位置安装压力计，以测量边坡水位。

1.2数据分析

土体压力计读数随降雨时间的变化如图2所示，压力计值表示了边坡中地下水位高度。降雨持续450 min后直至模型边坡崩塌过程中，随着降雨不断进行，压力计值不断增大，说明边坡模型内土体水位持续上升;降雨551 min后，坡面土体开始发生变形。实验过程发现，压力计值和孔隙水压力值增加不同步（如图3所示），这是因为压力计值是在测点周围的土体高度饱和后其读数才开始上升，而孔隙水压力在降雨过程中土体连续渗透作用下就会产生，并不是在土体高度饱和状态下才会发生。由于压力计读数与孔隙压力上升过程的趋势基本一致，因此可判断压力计读数是合理的。模型边坡从轻微变形到坍塌的过程如图4所示。图中①处，在深度约200 mm的地方坡体发生了初始裂缝和轻微变形;②处，地下水开始从模型坡体产生裂缝的地方渗出;③处，一定时间后，渗水点上方的斜坡表面开始出现裂缝;④处，以坡体顶部裂缝为边界的滑塌持续发生。另外从图4中可以观察到坡面下端的塌陷土变得泥泞。

自坡面有微小初期变形开始，边坡截面形状随时间的变化如图5所示。在初期变形发生10 min后边坡下端发生了较大的变形，并且发生了小规模的崩塌。随着崩坏规模逐渐变大，在坡面发生变形60 min后崩塌范围延伸到了边坡的顶部，最终形成大规模圆弧状滑动。

图3中亦显示了饱和度Sr和孔隙压力增量Δuw随着时间的变化，饱和度是根据土壤水分仪获得的体积含水量以及与制作模型时的相同ρd（ρd=1.15 g/cm3）计算出。Δuw為浇灌过程中孔隙水压的增量，其初始值为浇灌开始时的孔隙水压值。

饱和度在开始洒水降雨的初期阶段，边坡底端（M14和M15）土体的Sr值有所上升，之后此处Sr值约为0.8，高于其他区域。这是因为浸润面在斜坡底部较快到达防渗层（在本研究中防渗层为支撑上部边坡的坚实土层），随后形成水位使饱和度Sr值增加。从Δuw的变化可以看出，在降雨75 min左右，斜坡末端（P07）的Δuw上升，随着降雨的渗透，Δuw趋向于从边坡底端向模型中心（从P07到P01）方向上升。在模型底部饱和度Sr=0.8时，边坡中间部分（M12）的Sr值增大，当中部的Sr值和边坡底端的Sr值大致相同时，发生初始变形。由此可知，造成边坡初期变形的原因之一是由于边坡底端和中部水位升高，而导致边坡抗剪切强度下降[7]。

2洒水降雨时水位上升的模拟

2.1数值模型和条件

数值模型截面如图6所示，数值模型边界条件如图7所示。

数值模型的尺寸与模型实验尺寸相同。渗流数值分析边界条件：模型上部作为降雨入渗边界，支撑层的左端作为排水边界，模型的最底部和右缘均假定为不透水边界。降雨条件设置与实验相同。数值分析的初始条件是当安装在边坡和支撑层边界之间的压力值发生变化（降雨250 min），即支撑层的水位达到70 mm时，相当于给支撑层底面施加70 mm的压力水头。与模型实验土体相同压实度（Dc）试样的浸透排水实验结果如图8所示。

渗流分析中使用了水分特征曲线Van Genuchten模型[9]以及比渗透系数模型Mualen[10]。

θ=1+（α×ψ）n-m×（θs-θr）+θr，（1）

Kr=Se1/21-（1-Se1/m）m2，（2）

m=1-1/n，（3）

式中：θ为体积含水率;θr为残留体积含水率;θs为饱和时体积含水率;ψ为基质吸力，kPa;Se为有效饱和度;Kr为比渗透系数。

2.2数值分析

洒水降雨期间压力计高度hm随时间的变化如图9所示。这里表示了使用与模型实验干密度相同的试样进行定水头渗透实验得到的渗透系数k（k=klab）和使用与实验结果整合后逆向计算得到的渗透系数（k=kmod）的对比结果。

采用定水头渗透实验结果的分析中，Ma01的数值结果始终大于实验结果，Ma02在t=400 min左右的再现性较高，之后数值结果远大于实验结果。在t=400 min之前，Ma03的数值结果略低于实验结果，此后数值解比Ma02中的实验结果大很多。是因为所提供的雨水没有及时从模型边坡中排出，从而导致模型中的水位被过高计算。通过使用表1所示kmod数值分析，可以很好再现实验结果（图9中k=kmod）。

渗透坍塌部分的土体会从坡面流出。现推测是由于土体压实不均匀在坡体中产生了细小过水通道进而导致局部排水，这些过水通道的出现，导致整个模型实验的渗透系数大于渗透实验结果。另外，考虑到底部砾石材料的影响，使边坡底部渗流特性发生变化，数值分析结果与实验值相比大幅减小，难以取得整合性，从而对模型边坡整体的渗透系数产生较大影响。图10为坡面发生变形时，通过渗透系数值分析得到的流速矢量。

模型降雨过程中，在边坡发生变形区域附近，流速矢量在边坡表面变形位置的下方开始变大，且流速矢量沿水平向外变化，说明边坡底部发生初期变形可能是受渗透压作用的影响。

3弹塑性有限元对初期变形的再现模拟

3.1数值模型和条件

图11为数值模型截面的网格视图以及边界条件。

由图可知，边界条件是左右两端的垂直方向为自由端，水平方向为固定端。此外，分析条件将边坡水位设定为初期变形时从压力计上得到的数值。在此水位状态下，先进行自重应力分析，然后根据强度折减法确定安全系数和变形行为。岩土材料的本构方程遵从Mohr-Coulomb准则。非饱和土的有效应力根据Bishop[11]提出：

σ′=（σ-ua）+xg（ua-uw）=

σnet+xgs，（4）

式中：σ′为有效应力;σ为全应力;ua为孔隙气压;uw为孔隙水压;s为吸力;x为Bishop有效应力系数，0

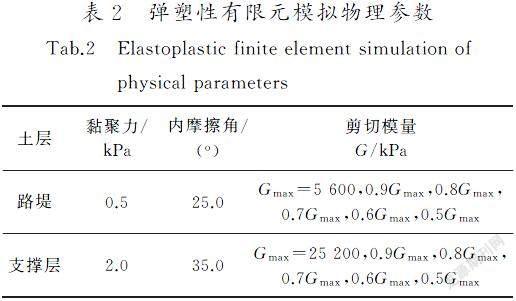
数值模拟中使用的物理参数如表2所示。

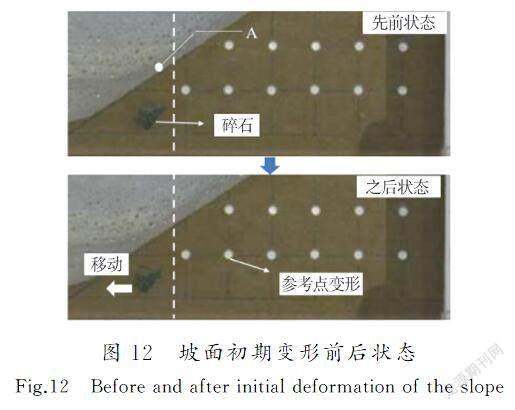
边坡发生初期变形前后的状态如图12所示。

可以观察到边坡底部设置的砾石向末端方向移动。此时坡面表层的位移量非常小，水平方向的位移量为0.5～1.5 mm。在本研究中，通过考虑微应变到小应变区域的变形系数来再现图12所示A点的位移实验结果。

岩土材料的變形系数随着有效应力的减小和应变的增大而减小并表现出强烈的非线性[12-13]。变形系数的大小对应力和应变分析很重要，因为会影响初期模拟计算。本研究中数值模型的微应变至小应变的变形系数可通过常规三轴压缩实验获得。本研究采用经验公式（6）和公式（7）[14]计算了边坡模型和支撑地层弹性区域的变形系数。

Gmax=1 400×f（e）×σ′m0.4，（6）

f（e）=（2.17-e）2/（1+e），（7）

式中：Gmax为微应变区的剪切模量;f（e）为孔隙比函数;σ′m为平均有效应力;e为孔隙比，由边坡和下部支撑土层的ρd和ρs计算得出。

3.2数值模拟结果分析

剪切模量变化差值ΔGmax与坡面变形量的关系如图13所示。

图10和图12中坡面变形，A点产生的水平位移为ux。在0.7Gmax左右时实验与数值模拟结果基本一致，表示可以通过降低无水位状态时的Gmax值来预测边坡初期变形状态。非饱和状态下，Gmax的增减除了受渗透压的影响外，也需考虑由于饱和度增加吸力降低导致有效应力减少的可能性[15]。

采用0.7Gmax得到的边坡底部变形的数值分析结果如图14所示。

数值模拟的边坡底部发生变形，表明数值分析结果与实验结果一致。在上述模拟中，假设变形系数减小的区域是整个模型边坡，为了确定模型的平均变形系数，式（6）中的垂直有效应力取值为模型中心所受垂直应力（H=300 mm）。

水平位移分布的模拟结果如图15所示。发生初期变形后持续降雨，650 min后发生大面积崩塌。发生大面积崩塌时模型内水位相比图15的水位仍处于上升状态。从图15可以看出，模拟结果发现发生大变形的区域与图16所示实验中的最终破坏区域基本一致。因此，在初期变形发生时，边坡变形系数（刚度）下降引起的微小变形极有可能形成潜在的滑移面，从而导致大面积崩塌。边坡出现初始变形后进一步降雨，地下水位上升引起的渗透压作用使得有效应力减小，从而导致边坡逐渐失稳。为了防止土体结构逐渐失稳而导致大面积崩塌，建议采取坡体排水等措施来防止边坡发生初期变形。由于边坡的初始微小变形很可能与潜在滑动面有关，因此，如果检测到这种微小变形，就必须考虑边坡发生崩塌或滑坡的可能性。

4结论

基于粉质砂土模型边坡降雨实验，通过土体饱和度和孔隙水压力的变化分析了边坡失稳的过程，通过饱和及非饱和渗流模拟再现边坡水位变化过程，采用弹塑性有限元法再现边坡初始变形状态，具体结论如下。

1）通过对渗流过程中地下水位上升进行分析，并使用弹塑性有限元法对模型实验随水位上升的初期变形进行数值模拟，发现：必须使用比渗透实验得到的渗透系数更大的数值进行计算，才能在数值分析中再现降雨过程中的边坡水位变化情况。

2）在模拟边坡变形系数降低的弹塑性有限元分析中，通过将弹性区域的变形系数降低30%得到与实验值相一致的数值解，由此可以看出，可以采用降低变形系数的数值模拟方法来预测边坡初期变形状态。

3）当前研究结果仅限于模型实验的再现且数值模拟基于边坡整体变形系数降低，而实际边坡破坏时，在渗透压作用下只有边坡底部局部变形系数的降低。

在今后研究中，需要对降雨实验和实际因降雨引起滑坡的案例进行更详细的数值分析，在此基础上建立更准确的边坡崩塌预测方法，提出更有效的滑坡防治措施。

参考文献/References：

[1]ORENSE R P.Slope failures triggered by heavy rainfall[J].Philippine Engineering Journal，2004，25（2）：73-90.

[2]TOHARI A，NISHIGAKI M，KOMATSU M.Laboratory rainfall-induced slope failure with moisture content measurement[J].Journal of Geotechnical and Geoenvironmental Engineering，2007，133（5）：575-587.

[3]張明礼，温智，董建华，等.考虑降雨作用的多年冻土区不同地表土质活动层水热过程差异分析[J].岩土力学，2020，41（5）：1549-1559.

ZHANG Mingli，WEN Zhi，DONG Jianhua，et al.Response of hydrothermal activity in different types of soil at ground surface to rainfall in permafrost region[J].Rock and Soil Mechanics，2020，41（5）：1549-1559.

[4]罗中宝.液压离心地震模拟振动台模型的建立及其控制策略研究[D].哈尔滨：哈尔滨工业大学，2015.

LUO Zhongbao.Modelling and Control Strategr Study of Hydraulic Centrifuge Shaker Used in Earthquake Simulation[D]Harbin：Harbin Institute of Technology，2015.

[5]LING H，LING H I.Centrifuge model simulations of rainfall-induced slope instability[J].Journal of Geotechnical and Geoenvironmental Engineering，2012，138（9）：1151-1157.

[6]胡嫚，吴飞，汪时机，等.基于光滑粒子法边坡失稳影响范围的模拟[J].重庆大学学报，2019，42（5）：56-65.

HU Man，WU Fei，WANG Shiji，et al.Modeling of influenced area after slope failure based on smoothed particle hydrodynamics （SPH）[J].Journal of Chongqing University，2019，42（5）：56-65.

[7]包一丁.排土场边坡稳定性评价及潜在滑坡灾害范围预测——以朱家包包排土场为例[D].长春：吉林大学，2020.

BAO Yiding.Stability Analysis and Landslide Failure Potential Forecasting of the Waste Dump：Zhujiabaobao Waste Dump Case Study[D]Changchun：Jilin University，2020.

[8]BUI H H，FUKAGAWA R，SAKO K，et al.Slope stability analysis and discontinuous slope failure simulation by elasto-plastic smoothed particle hydrodynamics（SPH）[J].Géotechnique，2011，61（7）：565-574.

[9]VAN GENUCHTEN M T.A closed form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal，1980，44（5）：892-898.

[10]MUALEM Y.A new model for predicting the hydraulic conductivity of unsaturated porous media[J].Water Resources Research，1976，12（3）：513-522.

[11]BISHOP A W，BLIGHT G E.Some aspects of effective stress in saturated and partly saturated soils[J].Geotechnique，1963，13（3）：177-197.

[12]TATSUOKA F.Laboratory stress-strain tests for developments in geotechnical engineering research and practice[C]//Proceedings of the Fifth International Symposium on Deformation Characteristics of Geomaterials.Amsterdam：IOS Press，2011：3-50.

[13]TATSUOKA F，IWASAKI T，FUKUSHIMA S，et al.Stress conditions and stress histories affecting shear modulus and damping of sand under cyclic loading[J].Soils and Foundations，1979，19（2）：29-43.

[14]IWASAKI T，TATSUOKA F.Effects of grain size and grading on dynamic shear moduli of sands[J].Soils and Foundations，1977，17（3）：19-35.

[15]KAWAJIRI S，SHIBUYA S，KATO S，et al.Effects of matric suction on elastic shear modulus for three unsaturated soils[C]//Proceedings of the 5th International Conference on Unsaturated Soils.[S.l.]：[S.n.]，2010：271-275.