智能小车路径选取算法比较

王思雯

摘  要：为解决智能装配系统装配零件运输最短时间问题，对智能小车在优化好的路径中寻求耗时最短的最优路径，在算法选择上提供了一些算法的核心思想以及结果比较。若考虑实际操作运输过程中的遮挡关系、障碍物的绕行等实际情况，为此提供了Dijkstra算法、A*算法、JPS算法、A*算法+JPS算法的优化这几个路径优化算法来对路径进行选择，其中Dijkstra算法搜索速度缓慢;A*算法时间效率上有所提高，但存在计算量过大和内耗过大的问题;JPS算法不能适应复杂地形，搜寻时间效率优于Dijkstra算法，但逊于A*算法;A*算法+JPS算法的优化精度更高，时间效率优于前3种算法，建议在智能小车实际应用中采用。

关键词：智能小车  Dijkstra算法  A*算法  JPS算法

中图分类号：TP301.6                        文献标识码：A                  文章编号：1674-098X（2021）05（c）-0118-03

Comparison of path selection algorithms for smart car

WANG Siwen

（Shenyang Ligong University， Shenyang，Liaoning Province， 110159 China）

Abstract： In order to solve the problem of the shortest transportation time of assembly parts in the intelligent assembly system， the core ideas of some algorithms and the comparison of results are provided for the smart car to seek the shortest time-consuming optimal path in the optimized path. Considering the occlusion relationship in the actual operation and transportation process and the detour of obstacles， Dijkstra algorithm， A* algorithm， JPS algorithm， A* algorithm + JPS algorithm are provided to select the path， in which Dijkstra algorithm has a slow search speed; A* the time efficiency of the algorithm is improved， but there are problems of too much computation and too much internal friction; JPS algorithm can not adapt to complex terrain， and the search time efficiency is better than Dijkstra algorithm， but inferior to A* algorithm. A* algorithm + JPS algorithm has higher optimization accuracy and better time efficiency than the first three algorithms. It is recommended to be applied in the practical application of smart car.

Key Words： Smart car; Dijkstra algorithm; A* algorithm.; JPS algorithm

智能裝配的前提是将货物零件装载运输到操作台再进行零件智能装配工作，智能小车选取货物零件的路径方式多种多样，最终目的就是使得小车以最优路径和最短时间将货物零件运送到操作台。若以移动智能小车选取的货物零件为起始点运送至操作台，就要规划智能小车的最优路径来避开障碍从而快速运送至操作台。本文将几个路径优化算法进行对比，其中Dijkstra算法、A*算法、JPS算法在搜寻路径方面都有较好的表现能力，在A*算法的基础之上结合JPS算法进行优化可以更高效、准确地完成路径搜索任务。

1  Dijkstra算法

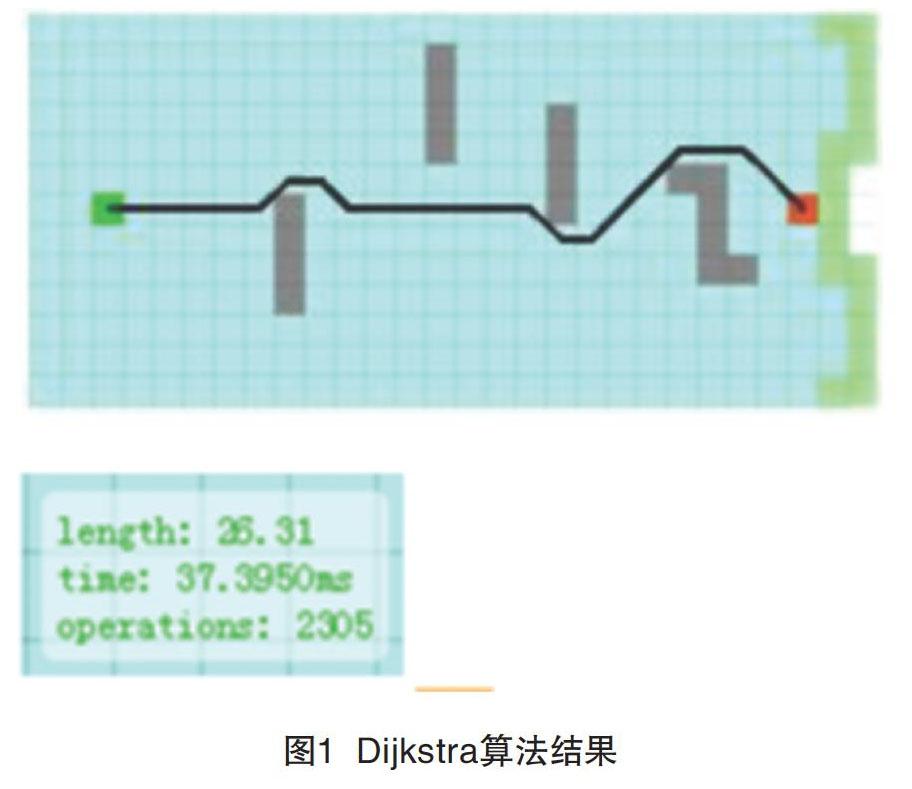
算法思想：首先需要制定起始点，还要创建2个合集S和U，S用来存放目前所求顶点到起始点最短路径的点合集，U则是存放还未求出最短路径的点，最后还要有一个数组用来存放源点到其他点的距离，开始时都设置为无穷大，以最短路径为原则更新数组。算法起始源点则为起始点，S中只包含源点，而U中有除源点外的所有顶点，从集合U中选出离起始点距离最短的点，并将该顶点从集合U中删除，加入集合S中，接着更新该顶点到源点的最短距离数值。后面的操作步骤则是以上一步骤求出的最短路径的顶点为操作对象进行相邻路径的延伸计算，直到遍历完所有顶点。成功率高，但搜索速度较为缓慢，如图1所示，搜索几乎遍历所有网格，假设每个栅格的长度为1，则遍历时间在37ms左右，规划路径长度为26.31，搜寻节点2305个。

2  A*算法

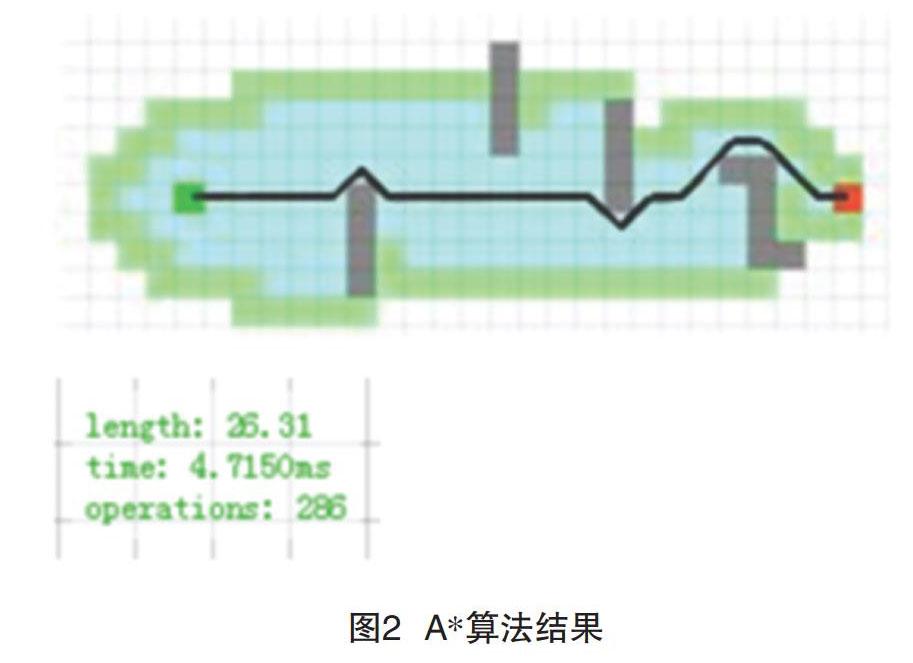
A*算法的基本思想可以概括为以起点开始不停地搜索周围的点（起始为8个点，已经被列为周围点的不会重复标记，阻挡也不会标记），再选出一个新的点（最优点）作为再进行循环搜索的起点，直至找到目标点。先创建2个列表，一个开启列表，用来储存起始点为始的周围点的寻路消耗;一个关闭列表，起始时就储存起始点，之后储存在列表中排序寻路消耗最小的点。需要注意的是，每次把周围的点放入起始列表时需要进行判断。（1）该点是不是阻挡点;（2）该点是否在开启列表或关闭列表中，以便周围生成的点都是新的点。同样在关闭列表中也要判断每次寻到的最优点是不是终点，若为终点则停止寻路，否则继续。但到目前为止，关闭列表中的最优点并不是最终的最优路径。如何根据关闭列表中的最优点寻找最优路径，这里将开启列表中的点都进行父格子记录标识，当最后关闭列表遍历完成之后，再以终点父格子目的进行路径回溯，即从终点开始寻找上一个最优点的父格子路径进行输出[1-3]。但A*算法存在严重的计算量过大和内耗过大问题，遍历时间为4.7150ms，规划路径长度为26.31，搜寻节点286个，效率相较Dijkstra算法明显提高，如图2所示。

3  JPS算法

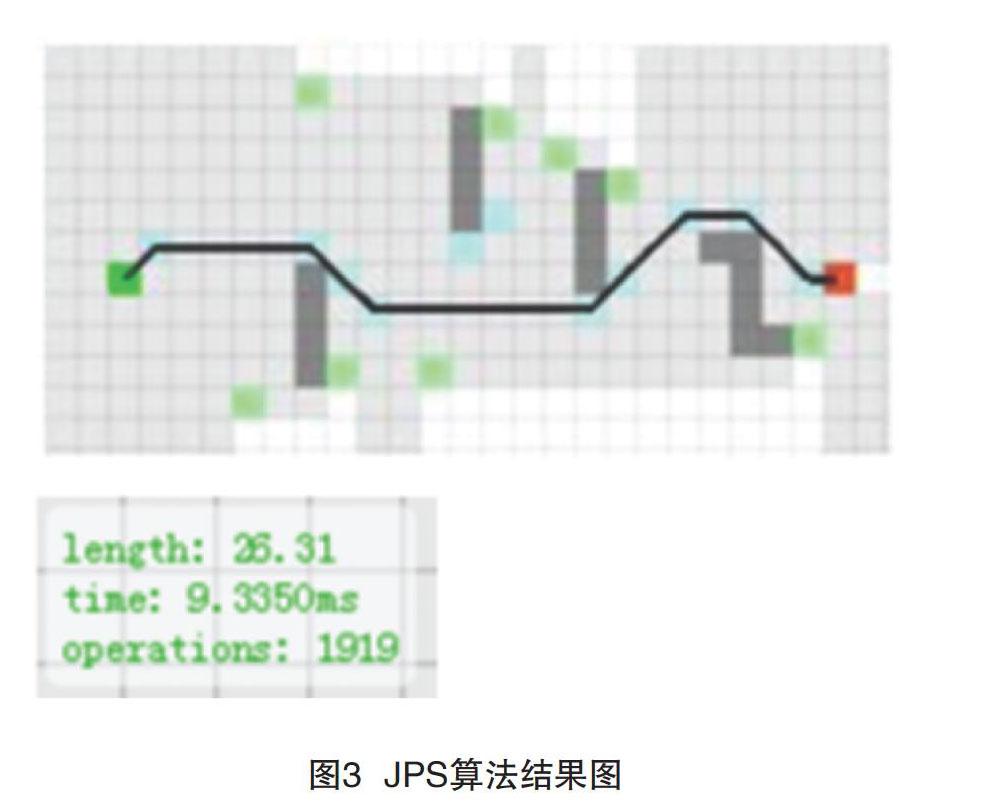
JPS算法的核心思想为根据当前点及周围点的特点来进行选择达到符合条件的点才能加入关闭列表或从开始列表中删除的操作。流程大致与A*算法相同，以寻找跳点作为搜索节点来进行遍历。首先强迫邻居的概念为当前节点的周围邻居点周圍有障碍时，且父节点到当前节点再到周围邻居节点的距离比父节点到其他点再到周围邻居点的值小，称这样的点为强迫邻居[4]。跳点的定义为，以邻居节点为原则，其一，若当前点有强迫邻居，则该点为跳点;其二，若该点为目的节点，则该点也为跳跃节点。与A*算法一样，都是在开始列表和关闭列表当中进行加入和删除的操作，只不过JPS算法是以强迫邻居和跳点搜寻作为寻找准则进行遍历。但JPS的缺点也很明显，图上的边不能带权重，也就是只能在较为规则的地图上进行搜寻操作，不能适应复杂地形[5-6]。如图3所示，遍历时间为9.3350ms，路径规划长度为26.31，搜寻节点1919个。

4  A*算法+JPS算法的优化

为解决A*算法速度慢内耗过大的问题，提出了改进A*算法并融合JPS算法的方法，如图4所示。首先改进A*算法评价函数（寻路消耗函数）的计算方式，在栅格图形应用实践上来看，以八方向为移动准则的话，物体的实际移动距离必定要大于A*算法自带的欧式距离值，而使用切比雪夫距离算法改进这个评价函数就可以很好地解决这个问题，开启列表中的寻路消耗路径值就可以为实际路径值，提高精度。接着在JPS算法的策略下改进A*算法，中心思想也是去除A*算法带来的巨大计算量和内耗。在进入算法前先将节点进行预处理，即将节点中的跳点和被迫邻居筛选出来，筛选方法与JPS算法的处理方式一致，相比于之前A*算法每个格子走一次的结果来看，以JPS算法为思想的算法的处理速度要快得多，一次处理跳跃的距离边长，精度也更高，效率也提高很多[7-9]。

5  结语

在选择运输零件的方式时，各算法都有着相对的优点和缺点。在栅格图形中，A*算法+JPS算法的优化也存在着路径曲折不够平滑的缺点，但A*算法+JPS算法的优化是最好的选择。

参考文献

[1] 张志文，张鹏，毛虎平，等.改进A*算法的机器人路径规划研究[J].电光与控制，2021，28（4）：21-25.

[2] 张丹红，陈文文，张华军，等.A～*算法与蚁群算法相结合的无人艇巡逻路径规划[J].华中科技大学学报：自然科学版，2020，48（6）：13-18.

[3] 任红格，胡鸿长，史涛.基于改进蚁群算法的移动机器人全局路径规划[J].华北理工大学学报：自然科学版，2021，43（2）：102-109.

[4] 马小陆，梅宏，王兵，等.基于JPS策略的改进RRT～*移动机器人全局路径规划算法[J].中国惯性技术学报，2020，28（6）：761-768.

[5] 刘辉，肖克，王京擘.基于改进蚁群算法的无人矿车路径规划研究[J].制造业自动化，2021，43（4）：108-112.

[6] 黄健萌，吴宇雄，林谢昭.移动机器人平滑JPS路径规划与轨迹优化方法[J].农业机械学报，2021，52（2）：21-29，121.

[7] None.JPS volume 51 issue 2 Cover and Back matter[J].British Journal of Political Science，2021，51（2）：23-26.

[8] 任云青.智能乒乓球自动捡球机器人的设计与实现[D].南京：南京邮电大学，2020.

[9] 郭健.机器人路径规划算法研究与应用[D].包头：内蒙古科技大学，2020.