基于CFD的进水管布设位置对沉降式固体颗粒排污影响的数值模拟

薛博茹，李永锋，胡艺萱1，，任效忠，赵云鹏，毕春伟

(1.大连海洋大学 设施渔业教育部重点实验室，辽宁 大连116023；2.大连海洋大学 海洋与土木工程学院，辽宁 大连 116023；3.大连海洋大学 水产与生命学院，辽宁 大连 116023；4.大连海洋大学 海洋科技与环境学院，辽宁 大连 116023；5.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

大力推进水产养殖机械装备的科技创新是中国加快水产养殖机械化发展的战略布局，中国农业农村部计划到2025年水产养殖机械化总体水平将达到50%以上。工厂化循环水养殖是水产养殖机械化的重要养殖模式与载体，契合“蓝色粮仓”国家渔业产业发展战略[1-4]。工厂化循环水养殖生产实践中，投入饵料与产出固体废弃物(包括残饵和粪便)的比例约为10∶3，长期滞留于养殖池底部的残饵和粪便等固体颗粒物极易发酵变质进而危害养殖生物健康[5]。Oca等[6]采用物理模型试验的方法，分析了进水方式对养殖池系统流场的影响，发现水平切向进水方式可有效减少低流速旋涡区，实现养殖池内更高、更均匀的流场条件，便于防止污泥沉降；Klebert等[7]运用数值模拟对封闭式海水网箱内颗粒扩散和固体冲刷进行了研究，得到了两者与池内流场的关系；冯德军等[8]通过物理模型试验及数值模拟的方法，分析了不同射流角度与射流流速工况下养殖池内流场与污物聚集的特点，检验了数值模拟结果的正确性与可行性。

目前，国内外关于池内水动力特性对养殖池系统集排污性能影响的数值研究较少，且以构建单一液相模型优化池内流场条件为主[9-13]，于林平等[5]运用数值模拟研究了进水管布设位置对单排污通道养殖池系统内水动力特性的影响，发现进水管布设于弧壁位置有利于单排污通道矩形圆弧角养殖池系统获得较优的流场条件。以于林平等[5]流场研究为基础，本文中构建固-液两相流数值计算模型，基于FLUENT离散相模型(DPM)对弧壁单管和直壁单管两种进水管布设位置下，不同密度和粒径的沉降式固体粒子的沉降规律和排出效率进行数值分析，旨在为完善养殖系统进水结构布设位置的选择提供理论依据，同时为提高养殖池系统的集排污性能设计提供参考。

1 数值模型

1.1 数值模型的理论与求解方法

本研究中主要通过调整养殖池系统内进水管布设位置，分析基于水动力条件优化对沉降式固体颗粒物沉降规律和排出效率的影响。首先构建固-液两相流数值计算模型，将流体作为连续介质，颗粒相作为离散相处理。养殖池内的流动以旋转和沉降为主，RNG k-ε湍流模型通过修正湍动黏度，尤其考虑了平均流动中的旋转及旋转流动情况，具有广泛的适用性和合理的计算精度，能更好地处理应变率高及流线弯曲程度较大的流动，更精准地模拟养殖池内的流场[14-15]。养殖池系统构建的固-液两相模型，液相是主体，与液相相比固相占比较小，颗粒物的体积分数占比远小于10%，且各颗粒沿自身轨道运动，可忽略颗粒物之间的相互作用，故FLUENT离散相(DPM)模型是其较优选择[16-17]。因此，本研究中选用RNG k-ε 湍流模型与离散相DPM模型相结合构建养殖池系统的固-液两相流数值计算模型，分析颗粒物的运动轨迹与排出效率。其中固-液两相流数值计算的假设如下：

1)养殖池系统保持恒温，不考虑温度影响；

2)养殖池内无养殖生物；

3)养殖池系统流体有黏性但不可压缩；

4)忽略颗粒物运动质量损失，即假设颗粒间不存在碰撞的质量损失及颗粒物的分解现象；

5)考虑萨夫曼升力和压力梯度力。

1.2 数值求解方法

本研究中，基于计算流体动力学(computational fluid dynamics，CFD)仿真软件FLUENT 16.0平台和戴尔服务器，根据试验及实际情况对池内流场即单一液相模型求解选择稳态(steady)控制方式；向池内添加固体颗粒物后即固-液两相流模式，对连续相模型(液相模型)求解仍然选取稳态(steady)控制方式，为更真实模拟固体颗粒物沉降规律和运行轨迹，针对固相模型考虑固-液双向耦合(interaction with continuous phase)，并开启非定常粒子追踪(unsteady particle tracking)方式。连续相和离散相均采用压力隐式求解方法，压力速度耦合方式选用SIMPLE算法，压力、动量基于二阶迎风离散格式(second order upwind)求解，湍流动能、湍动能耗散率基于一阶迎风离散格式(first order upwind)求解。设定压力和动量的亚松弛因子分别为0.3和0.7，湍动能与湍流耗散率的亚松弛因子为0.8，其他项保持常规设置[18]。对矩形圆弧角养殖池数值模型的进出口边界、交界面处理和壁面边界等条件进行设定。连续相模型和离散相颗粒的具体初始边界条件设置如表1所示。

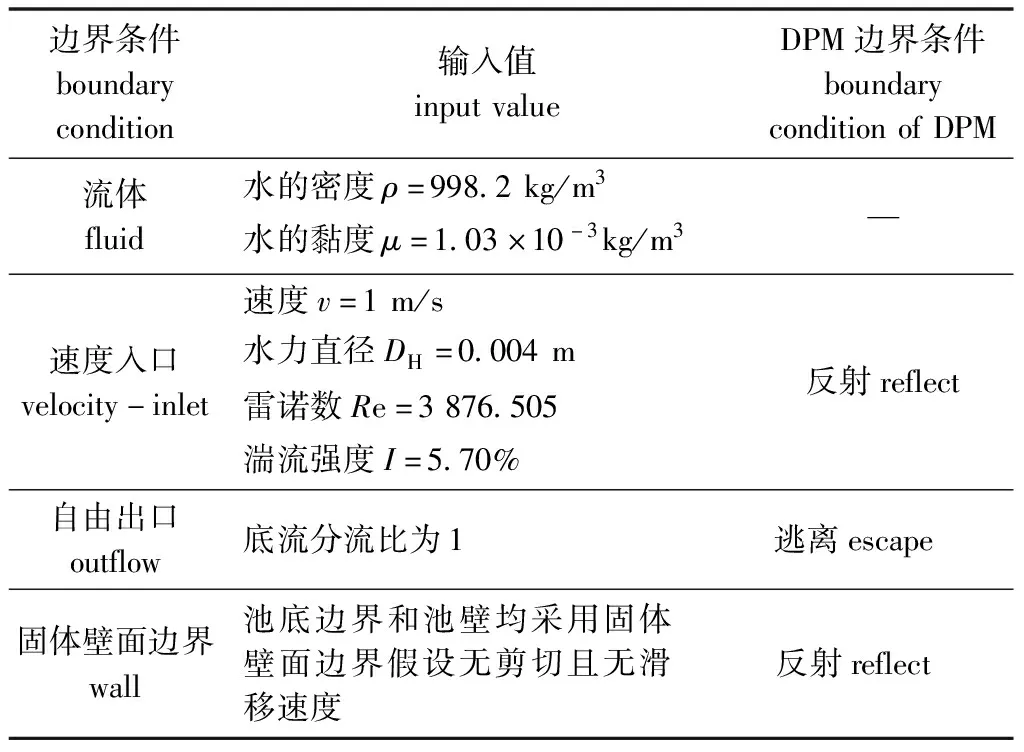
表1 数值计算初始边界条件

2 系统的几何构建与网格划分

2.1 矩形圆弧角养殖池模型建模

本研究中数值模拟所构建的矩形圆弧角养殖池模型参照工厂生产实践中养殖池的主体结构进行约为1∶8的比尺缩放，并对部分参数优化处理，模型各部分结构如图1所示(进水管布设于直边壁中间位置定义为直壁单管，进水管布设于弧边壁中间位置定义为弧壁单管)。其中，长宽比L/B=1∶1，相对弧宽比R/B=0.25，径深比B/H=5∶1，进径比Carc/Barc(弧壁单管)或C/B(直壁单管,其中C为射流孔位置到养殖池壁的水平距离，B为养殖池短边边长)为0.01。在不影响研究效果的前提下，将建模进行简化处理，养殖池高即为水深，且进水管与养殖池同高(均为200 mm)。流量恒定为0.470 m3/h，射流速度(v)为1 m/s，进水管结构在水深范围内均匀开12孔。

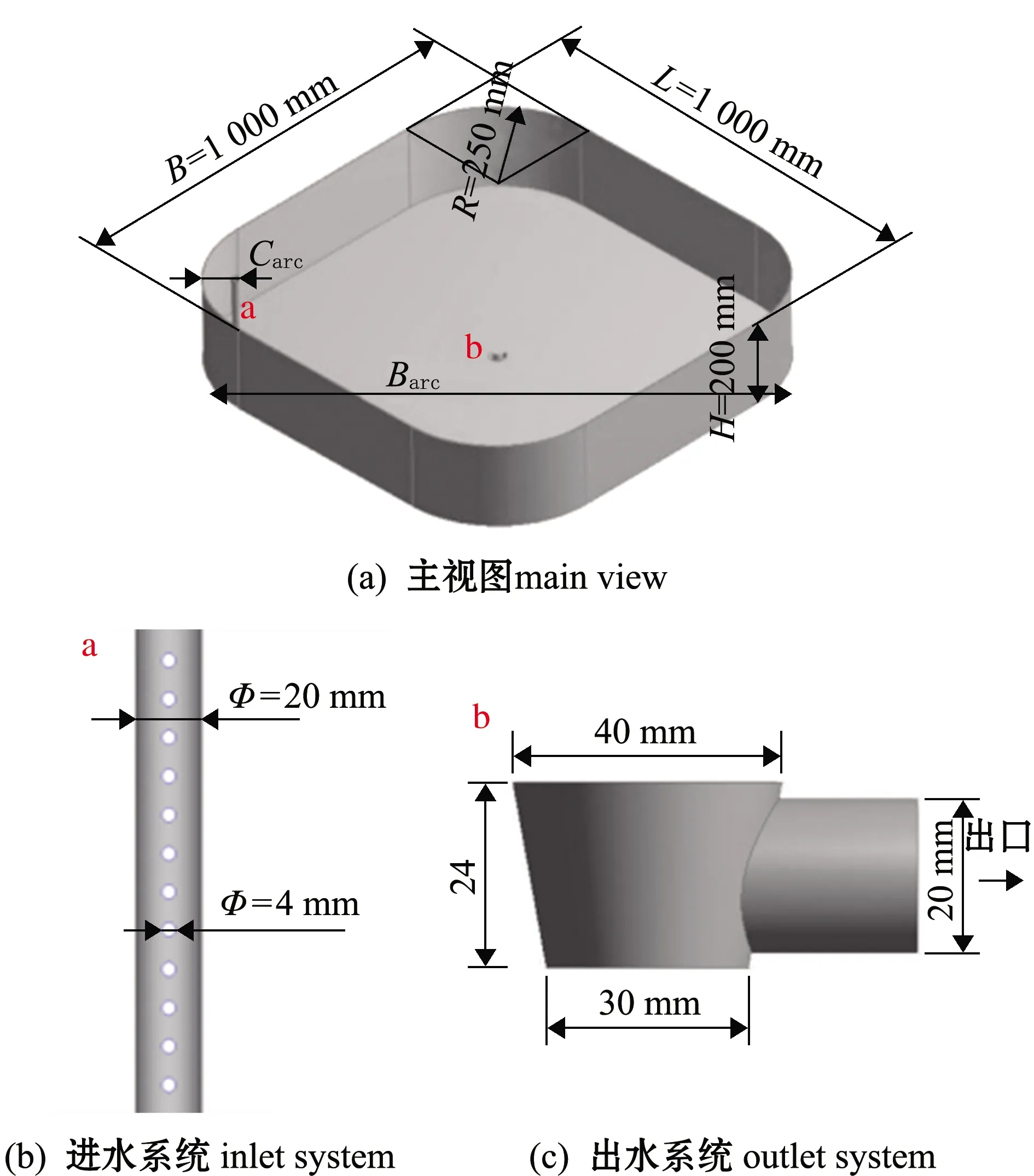
图1 矩形圆弧角养殖池模型图

2.2 网格划分与网格无关性验证

网格划分的质量和数量直接影响控制方程离散和数值模拟的精准度及计算时间，因而计算网格的分辨率应足够高，以保证数值求解的精度[19-21]。本研究中对固-液两相流模型进行数值模拟，为在保障计算精度的同时，兼顾提高计算效率与节约计算资源，选择多区域网格划分(muitizone)方式对养殖池内流场进行网格划分处理。养殖池主体部分采用六面体网格划分，进出水口等部分以四面体网格加密处理，并选用偏斜度(skewness)对网格进行质量评定。经网格质量检测得出，大部分网格的偏斜度为0～0.38，最大偏斜度为0.89，平均偏斜度为0.117 7，网格偏斜度满足要求，整体网格质量较高。图2给出了区域分解和网格划分示意图。

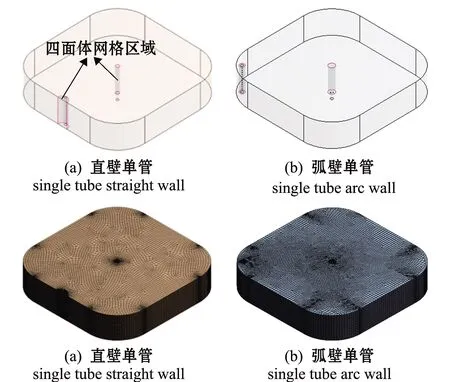
图2 固-液两相流模型和网格划分示意图

本研究中重点分析矩形圆弧角养殖池内的流场分布规律对养殖池系统集排污机制的影响。通过对比相同工况条件下，在同一位置处的监测流速变化，来评估网格尺寸对养殖池内流速分布模拟精度的影响，以获取用于数值计算的合理网格数量，其中，监测线是以养殖池中间层水平坐标为(0,-0.45)和(0,0.45)两点为端点的连线，即距离池底高度hz=0.1 m且进水管所在直线，每间隔0.05 m取一个监测点，共取19个监测点。监测线布设位置和不同尺寸网格的监测速度结果如图3所示。其中，网格数达到559 214(mesh-C)时，养殖池内整体流速大小和各个监测点速度分布的数值模拟结果均趋于稳定，且不再随网格数继续增加而发生明显变化。因此，选取网格数约为560 000，以此对各个研究工况进行数值分析。

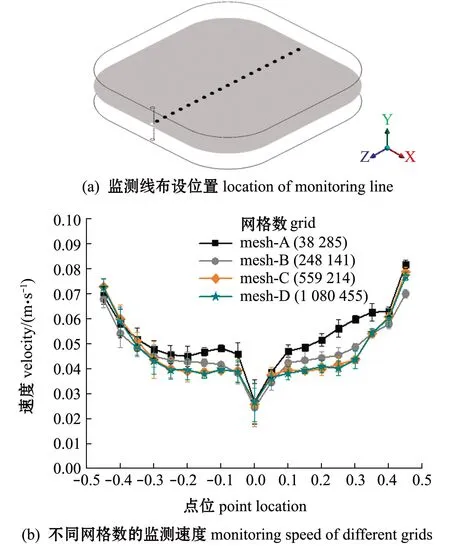
图3 网格无关性验证结果

3 数值模拟试验

3.1 物理模型试验和数值模拟的参数设置

3.1.1 物理验证试验 基于计算流体动力学可有效模拟池内流场特性，但数值模拟结果与湍流模型的选择、边界条件的设定，以及离散域的划分和相关监测点的设置等因素直接相关。为进一步验证本文所构建固-液两相流模型的合理性，建立与数值模型主体尺寸相同的物理试验模型，如图4所示，进水结构为对直双管(每管均匀开6孔，双管共12孔，流量恒定0.470 m3/h)，用常兴鲆鲽鱼类2#沉性饲料代替颗粒污染物(残饵)，通过比较数值模拟与物理模型试验，对比同一时刻固体颗粒物的累计排出效率，验证固-液两相流数值计算模型。

图4 物理模型试验实体图

物理模型试验过程：待养殖池内水体稳定运转后(约20 min)，向池内均匀撒入20 g饲料，从撒入时开始计时并每10 s拍摄一张监测照片，连续拍摄3 min并记录3 min内固体颗粒物累计排出情况。用Matlab软件将试验过程中拍摄的照片调整尺寸及清晰度后进行相应的分析，程序可自动识别出拍摄图片中颗粒物的总像素面积，再依据公式(1)计算出各时刻固体颗粒物累计排出率，且同一工况进行3次重复试验，观测数据合理性并取平均值。固体颗粒物累计排出率(K)计算公式为

K=(S-St)/S×100%。

(1)

其中：S为20 g颗粒物总像素面积(m2)；St为各时刻池内剩余颗粒物像素面积(m2)。

本研究中，通过比较数值模拟与物理模型试验同一时刻的固体颗粒物累计排出效率，验证固-液两相流数值计算模型。数值模拟是通过检测池内平均流速和残差曲线，在池内流场达到稳定运行后向养殖池系统注入与物理模型试验同参数的固体颗粒物。数值模拟过程中可直接监测出水口处颗粒物排出数量，以此计算固体颗粒物累计排出率。固体颗粒的物理性质：颗粒直径为2.0 mm，密度为1 250 kg/m3，形状系数φ=0.85(饲料为类圆柱体小颗粒)，通过换算与人工计数验证，得出20 g常兴鲆鲽鱼类2#沉性饲料约有900个小颗粒。

3.1.2 不同密度颗粒物排出率的参数设置 沉降于养殖池底部的固体颗粒物能否顺利排出，与养殖池底部流场特性尤其是底层流场流速可否达到颗粒物的起动速度密切相关。于林平等[5]和薛博茹等[19]以往的研究结果已表明，进径比参数为0.01时，弧壁单管养殖池系统内平均流速明显高于直壁单管系统，且养殖池系统流场均匀性尤其是底部流场特性也优于直壁单管系统。为进一步探索基于进水系统结构优化改善养殖池内尤其是池底流场条件，进而对促进矩形圆弧角养殖池系统的集排污性能的作用，本研究中选择5种密度分别为1 100、1 200、1 300、1 400、1 500 kg/m3的沉性饲料开展流场特性对不同特性饲料排污性能影响的数值模拟研究，颗粒在数值模型中的注入方式是在养殖池水面(hz=0.2 m)，以池心为圆心、0.45 m为半径的圆形范围内均匀撒布900个固体颗粒，养殖池内固相颗粒物撒布分布和前180 s沉降汇聚过程轨迹如图5所示。

图5 数值模拟颗粒物撒布图

此部分研究中涉及速度分布均匀性和颗粒沉降速度等的公式总结如下：

根据Masaló等[22]所定义的DU50参数分析养殖池流场速度均匀性，计算公式为

DU50=v50/vavg×100%。

(2)

其中:v50为养殖池中50%的较低速度的平均值(m/s)；vavg为养殖池中的平均速度(m/s)，该速度可以通过半径加权计算获得，即

vavg=∑viri/∑ri。

(3)

式中:vi为每个测量点的速度(m/s)；ri为测量点相对于养殖池中心的距离(m)。

颗粒沉降速度(vs，m/s)计算公式为

vs=H/ts

(4)

其中:H为养殖池水深(m)；ts为颗粒沉降至养殖池底部所需时间(s)。

3.1.3 不同粒径颗粒物排出率的参数设置 为探究矩形圆弧角养殖池系统内进水管布设位置对不同粒径的沉降式固体颗粒物排除效率的影响，选择7种粒径分别为1.0、1.5、2.0、2.5、3.0、3.5、4.0 mm的沉降式固体颗粒(颗粒物密度固定为1 300 kg/m3)，开展数值模拟研究。

3.2 模型验证结果

图6给出了不同时刻的数值模拟结果与物理模型试验结果对比，结果显示，模拟结果与试验结果的固体颗粒物累计排出率趋势高度一致，且各个监测时刻累计排出率的误差均在4%以内。可见，本研究中所构建的数值模型合理，可用于进水管布设位置对沉降式固体颗粒物排出率影响的数值研究。

图6 物理模型试验与数值模拟结果的比较

3.3 两种进水管位置工况下不同密度颗粒物的排出规律

从表2可见，注入固体粒子前后，养殖池系统内的平均流速和养殖池底部速度分布均匀性变化较小，主要原因是颗粒物的体积分数占比较小且处于分散分布状态，该系统内固-液两相流的作用主要体现在流场对固体颗粒的推动运动，而固体颗粒对流场的影响非常微弱。循环水养殖生产实践中，养殖池内残饵粪便等固体废弃物所占体积分数较小，亦不会对连续相即流体产生影响，证明本研究中固-液两相流模型符合循环水系统运行规律。与直壁单管养殖池系统相比，注粒后弧壁单管养殖池内的平均流速提高14.29%，池底速度分布均匀性提高12.88%。同体积固体颗粒物的密度越大，受重力作用影响越明显，因而沉降速度也越快。因此，在一定密度范围内，较大密度颗粒受水流拖拽力和重力的双重叠加影响，能快速沉降并排出池外，直接表现在颗粒物撒布初期(10 s内)，密度较大的颗粒排出率略高。

表2 固-液两相流模型特征量统计

图7给出了两种进水管布设位置工况下，不同密度颗粒物随时间的排出效率，其中，90 s时不同密度的固体颗粒物的排出率逐步趋于稳定，而150 s后固体颗粒物的排出率基本保持不变，故图8所给出的固体颗粒物的累计排出率以180 s时刻统计，此时的累计排出率基本代表了池内固体颗粒物的最终排出情况。与直壁单管养殖池系统相比，弧壁单管养殖池系统内1 100、1 200、1 300、1 400、1 500 kg/m35种密度的固体颗粒物累计排出率分别提高27.67%、32.80%、36.46%、29.62%和16.43%，充分说明池内的水动力条件与养殖池系统内固体颗粒物的排出效率密切相关，这是由于水动力条件是固体颗粒物运动的主要驱动力，进水管布设于弧壁位置有利于改善养殖池系统的集排污性能。此外，固体颗粒物的累计排出率与本身的属性密切相关。前10 s时间范围内，固体颗粒物的累计排出效率几乎不受密度影响，甚至密度较高的颗粒物累计排出率略高(图7)。

从图8可见：弧壁单管养殖池系统内，固体颗粒物最终累计排出率随颗粒密度的增大呈现先增加后降低的趋势，密度为1 300 kg/m3的颗粒物最终累计排出率较密度为1 100、1 200 kg/m3的颗粒物提高16.47%、4.70%，而当颗粒密度增加到1 400、1 500 kg/m3时，最终累计排出率较密度为1 300 kg/m3的颗粒物降低18.31%、40.16%；直壁单管养殖池系统内，颗粒物密度越大其最终排出率越低，密度为1 500 kg/m3的颗粒物最终累计排出率较密度为1 100 kg/m3的颗粒物降低22.09%。

3.4 两种进水管位置工况下不同粒径颗粒物的排出规律

图9给出了两种进水管布设位置工况下，不同粒径颗粒物随时间的排出效率，固体颗粒物撒布初期，由于粒径较大的颗粒物受重力作用明显，排出率略高于小粒径颗粒物的累计排出率。

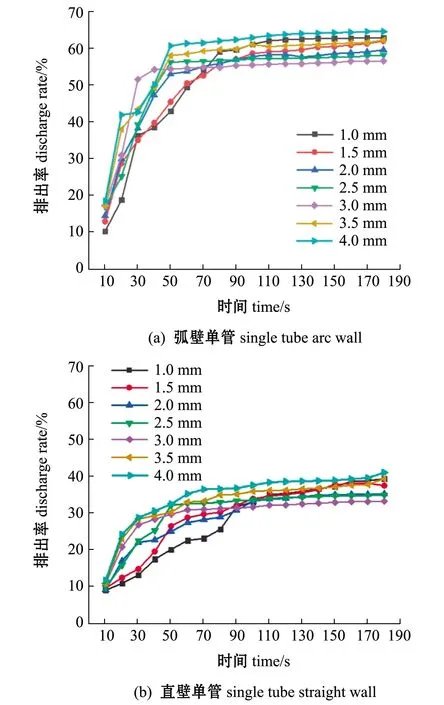
图9 不同粒径固体颗粒物排出率随时间的变化

图10给出了固体颗粒物的累计排出率(180 s)，与直壁单管养殖池系统相比，弧壁单管养殖池系统内粒径为1.0、1.5、2.0、2.5、3.0、3.5、4.0 mm的固体颗粒物排出率分别提高37.32%、39.42%、40.73%、39.77%、41.27%、33.40%、36.32%，进一步验证了池内的水动力条件与养殖池系统内固体颗粒物的排出效率密切相关。两种进水结构养殖池系统内，固体颗粒物最终累计排出率随颗粒粒径的增大均呈现先降低后增加的趋势；弧壁单管养殖池系统内，与粒径为3.0 mm的颗粒物相比，粒径为1.0、4.0 mm的颗粒物最终累计排出率分别提高9.70%、12.09%；直壁单管养殖池系统内，固体颗粒物排出率随粒径的增加，变化趋势和排出率上升与下降区间与弧壁单管养殖池相同，粒径为1.0、4.0 mm的颗粒物最终累计排出率较粒径为3.0 mm的颗粒物分别提高15.44%、12.90%。

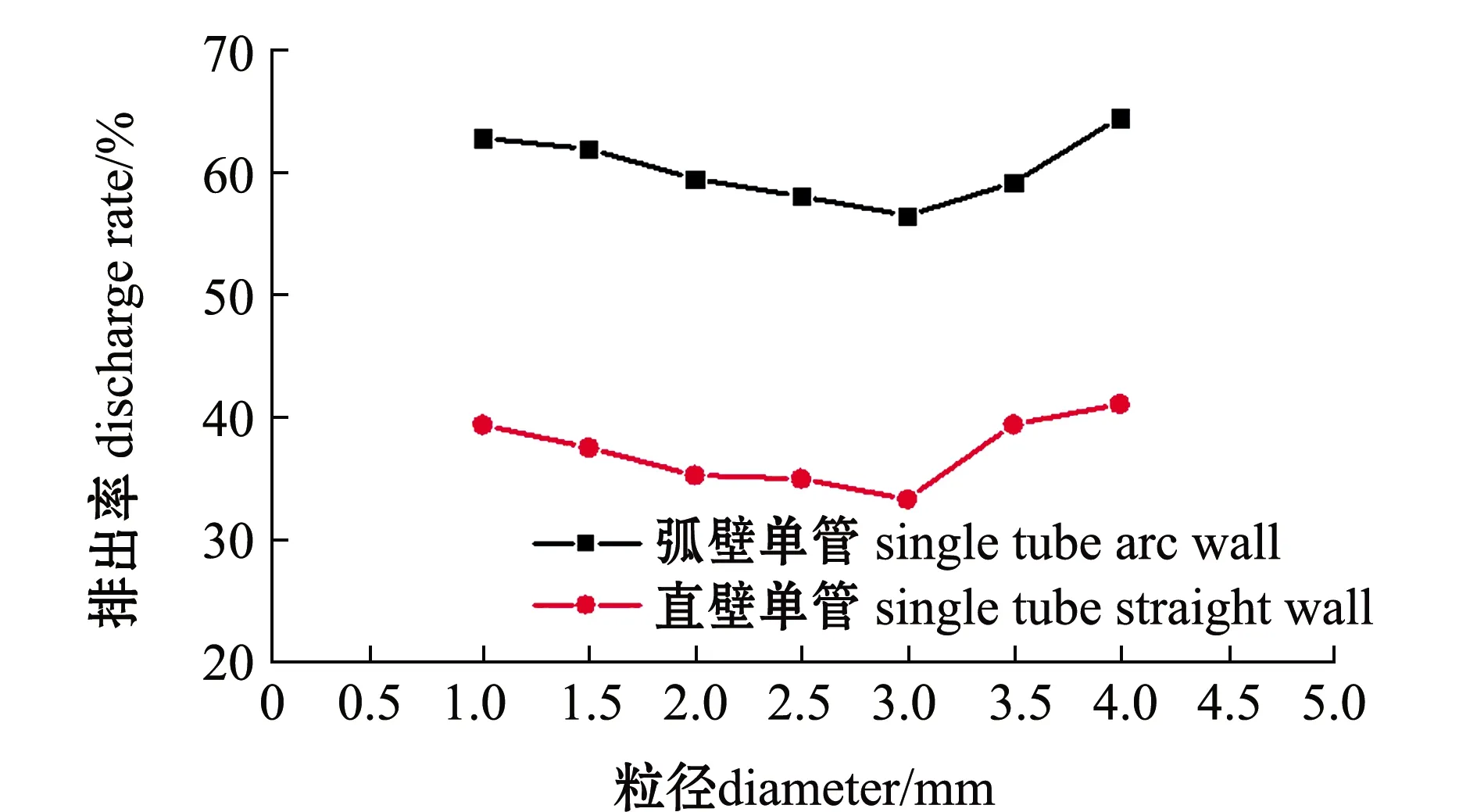
图10 不同粒径固体颗粒物的累计排出率

4 讨论

4.1 进水管布设位置对不同密度颗粒物排出率的影响

养殖池系统内的固体颗粒物主要由残饵和粪便组成，尽管其沉降和排出与自身属性密切相关[23]，但流场对其影响更为显著。本研究表明，弧壁单管养殖池系统内的平均速度较高且均匀性较好，其固体颗粒物累计排出率峰值出现在1 300 kg/m3，既优于低密度颗粒物(1 100、1 200 kg/m3)，也优于高密度颗粒物(1 400、1 500 kg/m3)。与弧壁单管养殖池系统相比，直壁单管养殖池系统内流场条件较差，固体颗粒密度从1 100 kg/m3增大到1 500 kg/m3过程中，其累计排出率呈现逐步降低的趋势，即当颗粒物密度为1 500 kg/m3时，其累计排出率最低。养殖池系统内的固体颗粒物受重力、升力、水流的拖曳力和与池底的摩擦力共同作用，其中重力和摩擦力是阻碍颗粒运动的力，升力和拖曳力是启动力。当养殖池系统内(尤其池底)的流速分布均匀且水体驱动力足够带动固体颗粒物运转时，密度较小颗粒物受到的水流升力和拖曳力较强，故颗粒物随水流在出水口附近旋转而不易排出；而当颗粒物密度较大时，其受重力作用较强，颗粒物沉降到池底后，水体驱动力不足，难以达到其启动速度，无法带动其向池心汇聚，故超过一定密度后固体颗粒物排出效率也下降。

4.2 进水管布设位置对不同粒径颗粒物排出率的影响

本研究中发现，随粒径的增加，两种进水管布设位置下的固体颗粒排出率均呈现先减小后增大的趋势，当颗粒物粒径较小(1.0、1.5 mm)和较大(3.5、4.0 mm)时，养殖池系统排污效果较好。这是由于较小粒径颗粒(1.0、1.5 mm)受水流驱动力作用较强，部分颗粒物进行离心运动，但由于颗粒物质量较小受重力影响较弱，基本不会产生沉积，故此时具有较好的排污效果。当颗粒物粒径增大(2.0、2.5、3.0 mm)时，水流流态所提供的驱动力让粒子无法完全做向心运动，此时部分固体颗粒呈现离心运动，且由于其受重力作用增强，发生离心运动的固体颗粒物在远离养殖池中心的池底发生沉积，所沉积的部分区域水动力条件较差，驱动力不足以带动颗粒向心汇聚，因此，养殖池系统内固体颗粒物的排出率下降。而大粒径颗粒物(3.5、4.0 mm)受养殖池系统内水力驱动力的影响最弱，因此，较低的运动速度使其离心运动程度减弱，甚至无法发生离心运动，故呈现随水流逐渐向养殖池中心排污口汇聚与排出的运动规律。

5 结论

本研究中，基于RNG k-ε湍流模型与离散相DPM模型相结合建立固-液两相流数值计算模型，对单通道排污矩形圆弧角养殖池内进水管布设位置下沉降式固体颗粒物的排污性能进行分析，在本文建立的养殖池系统与设计工况下得出以下结论：

1)通过与物理模型试验对比，证明本文所构建的固-液两相流模型合理、计算精度高，适用于循环水养殖池系统内固体颗粒物沉降规律和排污性能的研究。

2)单通道排污养殖池系统，进径比参数为0.01时，弧壁单管养殖池系统内同密度与同粒径固体颗粒物的累计排出效率均高于直壁单管养殖池系统且差异明显；同时，弧壁单管养殖池系统内流场条件优于直壁单管养殖池系统，充分说明固体颗粒物的累计排出率与池内流场特性密切相关，弧壁单管进水结构是优选布设位置。

3)养殖池系统内固体颗粒物的累计排出效率与颗粒本身属性密切相关，池内流场分布均匀且池底流速可以达到颗粒物驱动力时，受重力和水流共同影响，固体颗粒物的密度越大其累计排出效率越高；若池内流场条件均匀性较差且驱动力不足时，固体颗粒物密度越大其对应的累计排出率越低。

4)数值模拟计算中，固体颗粒累计排出率随粒径增大呈现先减后增长的趋势，不同粒径颗粒物受流场驱动力呈现不同程度的向心运动和离心运动状态，两种主要运动状态的强弱变化形成了不同的排污性能。本研究中固体颗粒物粒径为1.0、4.0 mm时，系统排污效果均较好。构建养殖池系统时需综合考虑养殖池内部流态和主要污物的自身特性，优化系统、改善流场均匀性并构建与污染物特性匹配较好的水动力条件，实现系统的良好的排污性能。