基于编队技术的无人机飞行控制策略研究
许鹏鹏,余祥功,夏昊天
(江苏航运职业技术学院,江苏南通,226010)
0 引言
当前,无人机已经在民用、军用很多领域内得到了广泛的使用。然而,随着其使用范围的持续扩张和所接任务难度的不断提高,之前使用的对单架无人机的操控策略早已无法满足各种新需求。单架无人机在执行复杂程度、难度都较高的任务时显得力不从心,难以保障工作效率及成功率[1]。为了解决单架无人机的不足之处,无人机编队这一作业形式的研发应运而生。无人机编队飞行模式主要是将两架或者两架以上无人机按照某个指定的编队构型去执行相关飞行任务,通过编队飞行能够顺利解决之前单架无人机在执行任时出现的各种问题。面对复杂程度比较高的任务时,通过并行模式,即便队伍中有一架无人机发生故障,也不会对完成任务造成任何不利影响。此外,在执行单架无人机无法完成的重、大型运输任务的时候,编队形式可以借助多架无人机之间的协同合作,在充分发挥小型无人机灵活性特长的同时,更加有效的完成飞行任务。
1 无人机编队控制技术
为满足飞行任务中所要求的各种变化,多架无人机按照指定的编队结构去飞行,其中包含设计、保持、重构队形以及避碰等各环节。在完成队形设计之后,无人机需要维持队形结构直至终点,且在飞行过程中需要实现避碰——能够成功避开途中所遇到的各种障碍或威胁[2]。在进行编队飞行时,固定好队形后的关键是如何保持住队形。队形能否得到保持,将会直接对作业情况和定位的精准程度造成很大影响。当无人机编队在保持队形进行固定飞行时,若遇到威胁或障碍就需要进行避碰,队形也可能会因此需要进行调整才能顺利抵达终点、完成飞行任务,即对编队进行重构。在特定情境下,只有重新构造编队才能更好地完成任务。因此,多无人机进行编队飞行时,需充分发挥编队保持、重构以及避障三大部分的技术[3]。
■1.1 障碍物威胁模型
无人机在飞行过程中会遇到很多障碍和威胁,并因此而影响其飞行轨迹以及任务的完成。为了能够更符合真实的飞行环境,并对本文中所用算法的有效性进行验证,本文创建了威胁模型,模拟真实飞行环境展开相关实验,所创建的障碍物威胁模型如下:

其中:(x,y)指的是地形在xoy轴的投影坐标,z指的是所创建的地形模型的高度,a,b,c,d,e,f,g则表示各个系数,借助这些系数的变化能够创建出各种不同地形。
■1.2 人工势能法
最初由Khatib提出来的APF(人工势能法),可分成斥力势场和引力势场两个部分,主要设计思路是构造障碍物周围的斥力场以及目标周围的引力场。按照势函数下降的方向,在势场值内反映出障碍物、目标分布和位置信息,并搜寻出安全的路径。其优势是:提高实时性、减少计算量。在搜索空间当中,如果以x表示UAV的位置向量,那么引力场、斥力场、复合势场三个函数如下:
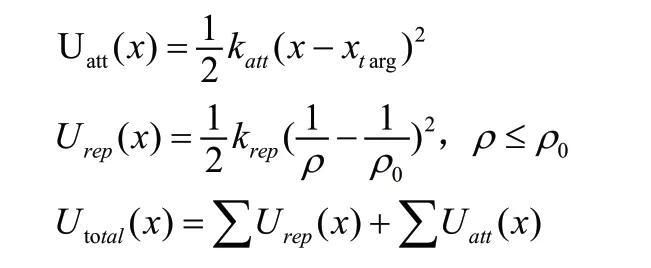
以此类推,每个点的势场力都能用上述公式计算得出,在合力作用之下,由出发点至终点。这种办法能够快速找出到达终点的路径,然而也有局限性,当终点附近存在障碍物的时候,无人机越接近终点的同时也会越接近障碍物,所受到的斥力也会越大,这时终点将不再是全局中最小的点,会导致无人机无法到达终点。在合力为0的时候,就会生成势场局部极点,无人机的进一步作业将不能再进行下去。而当障碍物密集存在的时候,无人机哪怕没有飞入局部极点,其路径也将发生较为复杂的震与抖动。
因此,APF算法更易于收缩至局部极小点,出现抖动现象和无法到达目标的问题,还会发生下列状况:
(1)传统的APF模型未考虑无人机势力在势力场内所发生的变化。当目标点靠近障碍物的时候,势场内就会生成引力,UAV便在引力作用之下朝着目标点移动,然而在此过程当中也会越来越靠近障碍物,无人机距离障碍物越近,便会受到越大的斥力,使其难以到达目标点[4]。倘若无人机与目标点之间有障碍物且二者共线,则按照经典APF算法得知,在无人机移向目标点时,一定会有某个点致使无人机所受到的合力为零并停止前进。
(2)由于引力与斥力所生成的合力突然变化而出现的抖动。当无人机靠近目标点时,障碍物四周的势场力会使合力出现变化,致使无人机下一个动作的角度发生很大改变,从而出现抖动的情况[5]。无人机如果在运动过程中发生至少持续两步方向角差θ,且大小在90<θ<180,则表明其出现了抖动。出现抖动情况,即使无人机有时仍可继续抖动着到达目标点,但其航迹飞行以及执行任务的效果都会受到影响,这种方式并不可行。另外,局部最小点APF法在无人机上的应用,主要是机体与目标点之间生成的引力牵引以及机体与障碍物之间生成的排斥力。机体在引力与斥力的合力作用下进行运动,发生目标点无法到达或抖动情况的时候,机体便极可能停留于局部最小点[6]。飞行环境内有时候会出现密集的障碍物,遇到这种情况,无人机很难绕道此区域到达目标点所在的位置,便需重选一些狭窄通道当作替代路径。但是,在狭窄通道中,这一点所受到的斥力可能会远大于目标点的引力,但是由于在经典的APF计算当中无人机的每一步运动都只会受到合力的作用,它就会陷在障碍中难以飞出,排斥力两边的力量都会将无人机陷至局部最小点,如图1所示。

图1 无人机陷至局部最小点
2 无人机编队队形控制算法
■2.1 编队队形模型的设计
本文研究的无人机编队飞行时所使用的结构为leaderfollower,例如:用一架leader及两架follower构成一个三角形结构的编队。在leader-follower结构中,编队内会设置一架无人机为leader(领航者),其余无人机则为follower,都跟着leader进行运动。Follower会参照leader所处位置的变化而调整其飞行方向和位置参数信息。Leader可用于指挥整支编队飞行的方向,在编队内可通过leader的位置参数信息计算出follower的预计位置,其他follower也会收到这一信息并飞至其在整个编队中的拟定位置。如图2所示,在模拟实验当中,可以借助于三角形编队结构以及leader的位置参数信息推算出编队中其他follower应处的位置参数信息和飞行路径。
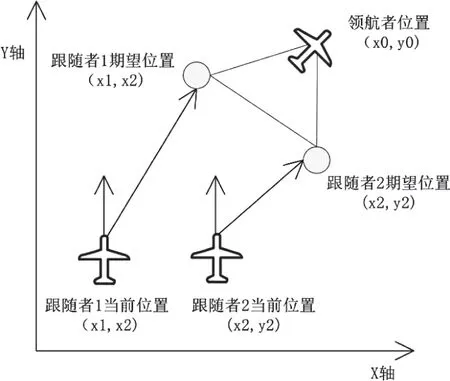
图2 三角形结构的leader-follower编队
■2.2 动态飞行编队方程
将编队内UAV数量设为N,Fc={UAVi|i=1,2,…,N}则可用于表示编队集合,UAV运动的动态方程就会如下:

式子内:(xi,yi) 代表的是UAV的坐标位置,vi为其速度;t代表采样的周期;xi代表无人机的航向角;av和ax分别代表速度及航向角时间常数;xic和vic则分别代表着航向角指令及速度指令。
■2.3 航迹规划的计算方法
无人机的航迹规划受到很多因素的制约,例如:机体性能、受障碍物影响的程度以及如何在复杂环境之下安全、准时地从起点到达终点。因此,规划航迹时必须在考虑以上制约因素的同时规划出最佳编队航迹,模拟出既能避免受障碍物影响出现碰撞危险又能很快到达目的地、完成任务的飞行路线[7]。因此,在对无人机进行航迹规划时,除了路径的长短,还必须保障其安全性。但是如此就可能出现多个目标,得到多个方案,在缺乏更多验证信息的时候,难以比较出这些方案中哪个更合适,因此需要找出更多适用方案[8]。当需要实现多重功能和最优效益时,就会出现四个甚至四个以上目标等待优化,有时目标甚至会多达10-15个。随着目标数量的增加,非支配解在随机选择当中所占比例也相应增大,目标向量集则呈指数级增长,使得搜索进展过慢。
■2.4 无人机多目标航迹规划的NSGA-Ⅱ算法
在规划航迹的时候,首先要确保无人机能够避开障碍物、避免发生无人机之间的碰撞,且在实现航迹约束条件(安全性、长度)的同时,为无人机规划出一条综合最佳方案。因此,问题则变成同时为多个目标进行优化,需要针对实际航迹规划中所遇到的问题创建出相应的模型,并利用NSGA-Ⅱ进化计算方法求解。在符合UAV飞行约束条件的前提之下,兼顾多重指标,同时优化航迹的安全性和长度,以更加有效地规划航迹。NSGA-Ⅱ进化计算方法的公式如下所示:

在执行上述操作后,可获得第1代子代,之后再由第2代开始翻倍种群的数量,对父子种群加以合并,快速非支配排序并计算出每一个非支配层个体的拥挤程度,从而选出合适的个体进入下一代。如此反复,直至迭代次数最大并取得最优解集,详细步骤如图3所示。

图3 NSGA-Ⅱ进化计算方法
3 仿真及结论
在航迹规划过程中,使用频率最高的三种路径算法是DEBA、BA和NSGA-Ⅱ。通过仿真得出图4所示的三维环境之下NSGA-Ⅱ、DEBA、BA的目标函数收敛曲线,对目标函数收敛曲线分析可得出:与路径规划仿真一致,以红色收敛线代表DEBA、蓝色收敛线代表BA、黑色收敛线代表NSGA-Ⅱ。特定算法的收敛速度取决于收敛线的斜率,因此NSGA-Ⅱ的收敛性能最佳,DEBA其次,而BA的收敛性能最不理想。相较于BA 和DEBA,NSGA-Ⅱ收敛速度最快,在数十次迭代操作之后,飞行目标函数最后能收敛至一个比较稳定的值,而这个稳定值多用于检验性能以及收敛精度。在迭代过程相同的情况下,NSGA-Ⅱ的收敛适应度则比BA和DEBA低,与最小收敛值相对应的是最低能量消耗和最短飞行路径长度。
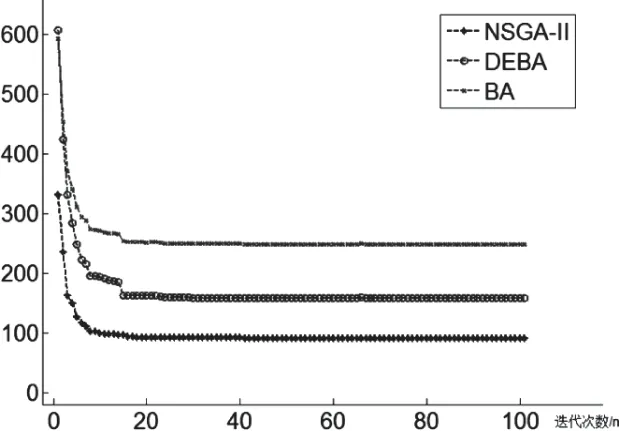
图4 目标函数收敛曲线

