基于经验模态分解算法的高铁沉降数据处理模型研究
申彦民

摘 要:针对高铁沉降观测存在观测噪声等情况,利用经验模态分解算法对银西高铁银吴段沉降观测数据进行分解处理,利用小波去噪算法完成分解后高频本征模态函数的去噪实验。实验结果表明,相对于传统小波去噪算法,基于EMD分解算法的小波去噪实验具有更好的信噪比和误差均方根,EMD-WD去噪算法在SNR方面提高2.481db,在RMSE方面提高0.027。
关键词:高铁变形监测 经验模态分解算法 小波降噪 信噪比
中图分类号:U212 文献标识码:A文章编号:1674-098X(2021)05(b)-0146-04
The Research on High Speed rail Settlement Data Processing Model based on Empirical Mode Decomposition Algorithm
SHEN Yanmin
(China Construction Communications Construction Group Co., Ltd., Beijing, 100166 China)
Abstract: In view of the observation noise existing in the settlement observation of high-speed railway, the empirical mode decomposition algorithm is used to decompose the settlement observation data of yinwu section of Yinxi high-speed railway, and the wavelet denoising algorithm is used to complete the denoising experiment of high-frequency eigenmode function after decomposition. The experimental results show that compared with the traditional wavelet de-noising algorithm, the wavelet de-noising experiment based on EMD decomposition algorithm has better signal-to-noise ratio and root mean square error. EMD-WD de-noising algorithm improves SNR by 2.481db and RMSE by 0.027.
Key Words: Deformation monitoring; EMD; Wavelet; SNR
高速铁路是人们出行的重要工具之一,为了保证高铁出行的安全性和可靠性,对高铁铁轨路基的累计沉降量监测就变得尤为重要。在铁轨沉降监测过程中,测量值将受到多种因素的影响导致误差积累,使其观测量并不能充分、准确的反映高速铁路的真实变形。为解决上述问题,本文将经验模态分解(Empirical Mode Decomposition, EMD)算法引入高铁数据预处理实验,使用EMD算法将实验数据分成不同组别的本征模态函数(Intrinsic Mode Function, IMF),利用不同组别的IMF函数来反映实验数据各个维度的数据变化情况,由于EMD分解算法特性,导致各组别的IMF函数具有高频到低频的特性[1]。本文将通过选取高频IMF函数作为小波去噪(Wavelet Denoising, WD)算法的主要去噪对象,完成本文使用的EMD-WD算法的去噪实验,同时对比WD算法去噪实验,通过信噪比值、均方根与相关系数作为实验的去噪结果评价指标,研究EMD-WD算法的去噪性能。
1 算法基本原理
1.1 EMD算法
经验模态分解算法不需要知道信号的先验信息,可以将所有的时间序列信号分解成为不同组别的IMF函数,利用具有不同频率的IMF函数表示原始的时间序列信号,该方式可以充分反映原始時间序列信号的内部变化[2]。IMF筛选条件为:(1)局部极值点的个数和零点个数相差必须小于等于1;(2)构成IMF函数的极大值包络线均值与极小值包络的均值为0。
1.2 小波去噪算法简介
小波分析与傅里叶分析不同的是:小波分析的基函数不唯一,不同的小波基函数可以适用于不同的实验数据分析[3]。常见的小波基函数有:Haar小波、Marr小波、Daubechies(db)小波等。在众多的学者中,Donoho博士做了大量小波去噪研究工作后提出了小波阈值去噪,后人在此基础上运用合理的参数解决各种现实应用中的降噪问题。在小波阈值理论中,阈值分为硬阈值和软阈值[4]。
阈值在去噪过程中起了决定性的作用,所以大小选取至关重要。如果阈值选取太小,那么经处理后的噪声系数过多保留,达不到去噪的目的;如果阈值选取过大,那么就会丢失一部分真实信号,使信号失真。最常用的阈值确定方法为固定阈值法[5]。公式如(1)所示。
(1)
式中,λ为阈值,N为时间序列信号的长度,为高斯白噪声。
1.3 EMD-WD模型
本文使用的EMD-WD去噪模型,采用EMD算法完成实验数据的分解预处理,得到不同组别的IMF函数,利用WD算法完成高频组别的IMF函数,然后与其他组别的IMF函数进行重构,完成本次的EMD-WD去噪实验。本文将分别采用小波作为文章使用的小波基函数,选用2、3、4作为EMD-WD模型的分解层数,选用固定阈值法作为EMD-WD模型的阈值,完成去噪实验。
本文将使用均方根误差、信噪比和相关系数作为文章算例去噪结果的精度评价指标。
均方根误差(Root Mean Square Error, RMSE):原始数据与去噪后的数据之间的方差的平方根[6]。其表达式如下:
(2)
式中,N表示信号的大小,X0是原始信号,χ是小波去噪后的信号。
信噪比(Signal-to-Noise Ratio, SNR),是衡量数据中噪声的常用指标,所以常被用来衡量去噪效果的方式,单位是db,信噪比越高则去噪效果越好,其表达式如下。
(3)
式中,为真实数据的能量,为噪声的能量。
2 EMD-WD去噪模型建立与实现
2.1 实验数据概况
本文选用的数据为银西铁路吴忠至银川客专铁路第三标,线路起止里程为DK599+587.08~DK639+150,长度为39.563km。本文选用的4个地点的数据分别为DK623+175、DK623+194、DK623+204、DK623+250,数据测量周期从2017年4月—2018年4月,为期1年。
2.2 算例分析
本文分别针对银西铁路吴忠至银川客专铁路某监测区域的4个地点的数据作为文章实验数据,分别选用不同的小波基函数和分解层数完成EMD-WD算法在4组实验数据的去噪实验。通过实验分析,当小波基函数为db3,小波去噪分解层数为3层时,去噪效果最好。因此本文仅体现小波基函数为db3,分解层数为3层实验条件下的去噪结果。
图1、图2、3图分别为固定阈值、软阈值、硬阈值条件下的EMD-WD算法的去噪情况比较,由于文章篇幅限制,本处只体现实验地点1的去噪情况。从图中可以看出EMD-WD算法,WD算法都与原始数据保持类似的变化趋势,但是并不能通过去噪情况图完全反映去噪的情况,需结合实验地点去噪情况统计表分析本文使用去噪方法的精度。
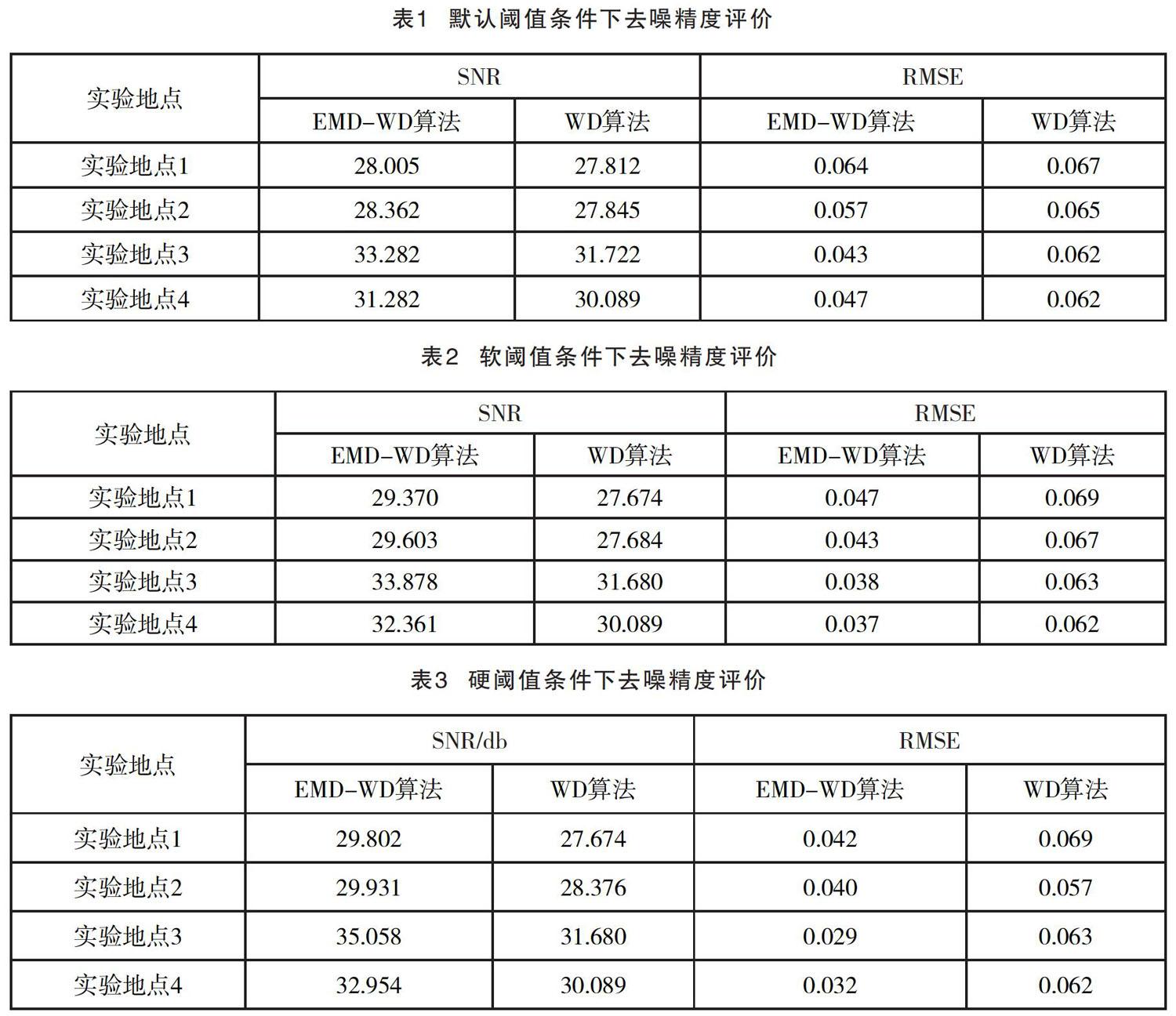
本文分别完成默认阈值、软阈值、硬阈值条件下的EMD-WD算法的去噪实验,分解层数为3層,小波基函数为db3条件下,实验情况如表1至表3所示。
通过表1至表3可以看出,EMD-WD算法和WD算法在不同阈值条件下去噪精度评价,通过横向比较各表可知,在不同阈值条件下 EMD-WD算法相对WD算法有不同程度去噪水平上的提升。通过纵向比较各表可知硬阈值在SNR和RMSE两方面相对默认阈值、软阈值去噪水平的优越性。
为衡量高铁路基沉降趋于稳定,是否满足铺设轨道的一个重要数学指标,即时间和累积沉降量的相关系数要大于0.92。文章为研究EMD-WD算法的实际应用情况,本文将该方法去噪后获取的相关系数统计如表4所示。
表4为不同实验数据在固定阈值、软阈值、硬阈值3种不同种类的去噪实验中的相关系数统计情况,通过观察表4可知在固定阈值、软阈值、硬阈值三种不同种类的去噪实验中,EMD-WD算法优化了原始数据的相关系数,使其可以充分反映高铁累计沉降量的实际情况,为后期高铁建设提供更为准确的数据支持。
3 结语
本文主要研究了EMD理论和小波分析理论,利用EMD算法完成高铁沉降数据的分解预处理,利用小波去噪技术对高频IMF分量进行降噪处理。实验结果显示,利用EMD算法改进的小波去噪算法相对直接利用小波的去噪算法具有信噪比更优、误差均方根更小的优势。通过比较不同组别的实验,发现本文采用的EMD-WD去噪算法,在小波基函数为db3,分解层数为3层的硬阈值去噪实验中,去噪效果最优,相对于只是用小波去噪算法,EMD-WD去噪算法在SNR方面提高2.481db,在RMSE方面减少0.027。本文完成了EMD-WD去噪算法在相关系数方面的应用研究,实验数据显示,在固定阈值、软阈值、硬阈值去噪实验中,经过EMD-WD算法的实验数据,其相关系数相对原始数据有不同程度提高,证明了EMD-WD算法的优越性。本文分别以信噪比、均方根误差和相关系数3个指数作为评价EMD-WD算法的去噪评价指标,实验结果表明利用EMD算法优化小波去噪算法,具有更优秀的去噪能力,为高铁沉降数据降噪处理提供了新的研究思路。
参考文献
[1] 汤俊,李垠健,高鑫.基于CEEMDAN的GNSS变形监测去噪方法[J].大地测量与地球动力学,2021,41(4):408-412.
[2] 杨帆,谢洋洋,邵阳.小波去噪的灰色最小二乘支持向量机变形预测[J].测绘科学, 2017,42(10):134-137.
[3] Guo T, Deng Z. An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing[J].Applied Acoustics,2017(127):46-62.
[4] 王建敏,马天明,祝会忠.BDS/GPS整周模糊度实时快速解算[J].中国矿业大学学报,2017,46(3):672-678.
[5] 陈旭升,张献州,蒋英豪,等.局部均值分解的新小波阈值去噪法及其应用[J].测绘科学,2021,46(2):48-54.
[6] 姜刚,李举,陈盟,等.灰色-小波神经网络支持下对地铁工程沉降变形的预测[J].测绘通报,2019(5):60-63.

